河道汇流演算方法对比分析与研究

龚 定，李致家，臧帅宏，孙明坤

(河海大学水文水资源学院，江苏 南京 210098)

河道汇流演算实质上是一个水力学问题，由于存在需要较多的河道实测断面资料与较长的计算耗时等问题，水文学家发展了水文学方法和简化的水力学方法[1-3]。1938年McCarthy提出一种原始的水文洪水演算方法，即Muskingum法[4-5]，将所有的地形特征和河段的水力学特性归为模型的系列线性参数[6]。20世纪60年代，赵人俊[1]推导出分段马斯京根法连续演算的通用公式，解决了长河道预见期短的问题。实际河道水流条件复杂多变，河道的水力特性可能随沿程发生变化，又形成了各种非线性的演算方法。1969年Cunge在Muskingum法的基础上提出了Muskingum-Cunge(MC)法[7]；1978年Pouce等在Cunge法的基础上，考虑波速的变动问题，将Muskingum演算法扩展到时间可变参数[8]，提出了变动参数MC演算法(以下简称MC演算法)。使用线性参数的Muskingum法很好地保证了演算过程中河段的蓄量平衡，但MC演算法演算过程导致的质量损失随着河底坡度的减小而增加[9-10]。针对MC演算法中的质量不守恒问题，2007年Todini等[11-14]提出Muskingum-Cunge-Todini(MCT)可变参数法，引入了修正因子和校正系数，进一步完善了河道汇流演算方法。

河道汇流演算在流域洪水预报中起着关键性的作用。我国幅员辽阔，流域特点各不相同，汇流条件复杂[15-16]。在汇流过程中，河道内水流运动受地形影响较大[17]，传统的河道演算方法难以准确地描述河道的汇流特性，降低了洪水预报的精度[18-20]。MC演算法和MCT可变参数法在国外已经取得较为广泛的应用[21-22]，在国内，非线性和变参数河道汇流演算法在生产上还没有较为成熟的理论和应用[1]。

本文在分段马斯京根法的基础上选用考虑河道断面形状和水力特性的MC演算法和MCT可变参数法对沅水流域沅陵站—王家河站河段进行河道汇流演算，对比分析考虑真实河道特性的汇流演算方法模拟效果。

1 方 法 介 绍

1.1 MC演算法

Ponce和Yevjevich在没有改变问题实质的基础上[8]，提出了出流系数的表达式：

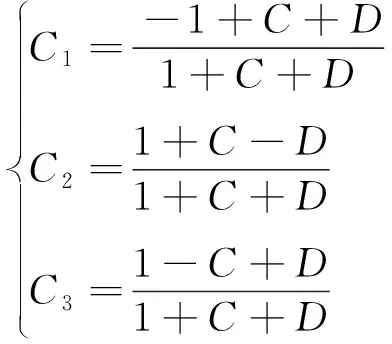
(1)

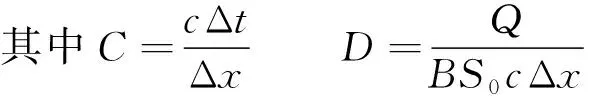
式中：C1、C2、C3为演算系数；C、D分别为库朗数和单元格雷诺数，即物理和数字扩散率；Δx为河流或河道被分割计算区段的长度，m；Δt为积分时间步长，s；B为地表宽度，m；S0为底坡坡度；Q为参比流量，m3/s；c为波速，m/s。

1.2 MCT可变参数法

MCT可变参数法并没有改变MC演算法的简单性，但同时又解决了物质守恒的问题[23]。由式(1)可得

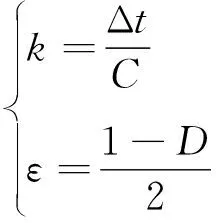
(2)

MC演算法中，在一个时间步长内，k和ε不随时间变化[24]。即在计算相邻时刻的河段蓄量时，使用的k和ε是不一致的，在t时刻，有：

(3)

式中下标代表相邻两个河段。可以得到：

(4)

式中St为t时刻的河段槽蓄量，上标代表同一个河段蓄量的不同计算方式，这就造成了在连续时段下，蓄量出现不守恒的情况。在MCT可变参数法中，k和ε在一个时间步长内变化，在每个时间步长分别产生两个库朗数和单元格雷诺数，解决了式(4)蓄量不平衡的问题。

MCT可变参数法演算系数表示为

(5)

分段马斯京根法、MC演算法和MCT可变参数法的出流公式为

Ot+Δt=C1It+Δt+C2It+C3Ot

(6)

式中：Ot、Ot+Δt分别为t和t+Δt时刻下断面出流，m3/s；It、It+Δt分别为t和t+Δt时刻的上断面入流，m3/s。

2 研 究 流 域

沅陵站—王家河站河段地处湖南省西北部，怀化市北端，属于沅水流域，为亚热带季风气候区，位于110°05′31″E～111°06′27″E、28°04′48″N～29°02′26″N之间，区间面积约为4 100 km2。在长期的水流侵蚀、切割和新构造运动的作用下，形成南北高起、中间陷落的沅陵谷地地貌。境内山峦重叠，溪河纵横，地形复杂。春秋两季气旋活动频繁，冷暖变化大。春季及初夏多锋面雨，夏秋之际多台风。沅陵县属于中亚热带季风湿润气候，阳光充足，雨量充沛，四季分明，年平均气温16.7℃。一般8月最高，1月最低。年均降水量1 400 mm左右，常有局部暴雨出现，夏季降水量占全年雨量的40%。研究区域面积为6 456 km2，河段总长112 km，底坡较缓、较均匀，比降约为0.000 277，河槽糙率n为0.022～0.030。图1为沅陵站—王家河站河段所处流域示意图，河道径流主要依靠上游来水，旁侧只有小支流汇入，入流量均不大，因此沅陵站—王家河站河段干流受支流来水影响较小，本文不予考虑，可以看成单一河道。

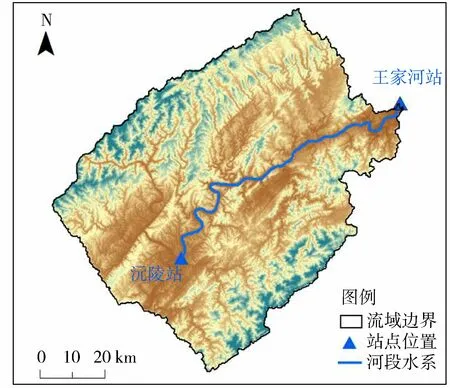
图1 研究河段示意图Fig.1 Map of study channel

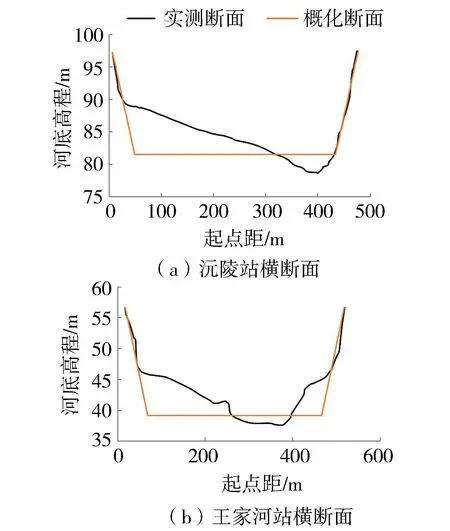
图2 沅陵站—王家河站河段河道断面概化Fig.2 Generalized figure of Yuanling-Wangjiahe channel section

3 参 数 率 定

3.1 河道断面概化

根据沅陵站—王家河站河段的实测大断面资料，考虑对河道横断面进行三角形概化或梯形概化。

a.三角形概化。概化过程中保留河道水深，但会损失河道边坡和过水面积的精度，而三角形断面河底宽度为0 m，不符合实际断面情况。

b.梯形概化。概化后基本与河道原断面边坡和过水面积一致，损失部分水深。

因此，根据河段实际断面特性，选择将河道断面形状概化为梯形。其中沅陵站河道横断面概化后的河底宽度为382.4 m，边坡坡度约为20.3°。王家河站河道横断面概化后的河底宽度为390.5 m，边坡坡度约为17.3°。河道概化图见图2。沅陵站和王家河站均在流域干流上，实际断面情况比较接近，采用两个站断面概化后的算术均值作为汇流演算方法的断面参数值，即河道河底宽度为386.4 m，边坡坡度为18.8°。图2中河段左岸为零点。

3.2 汇流演算方法参数率定

在沅陵站—王家河站河段流量资料中，选取1979—1985年共15场洪水进行河道流量演算。其中9场用于参数率定，6场用于方法验证。

将3种汇流演算方法的时间步长定为1 h，通过经验推求法，确定分段马斯京根法参数为：河段数为10，蓄量参数k=1 h，流量比重系数ε=0.45。

MC演算法和MCT可变参数法考虑河道断面的形状和水力特性，在实际率定过程中，当n分别为0.03和0.02时，后者河道汇流方法的模拟精度明显更高。河道汇流方法的模拟精度表现出与河道水力因素有关，分析其原因为所选洪水中多数场次流量量级超过1万m3/s，流量偏高造成对河道的冲刷程度更高，使得实际糙率变低，说明汇流方法考虑河道特性具有可行性。汇流方法使用牛顿法对参比流量和水位进行迭代计算[25]，具体河道参数为：河段数15，S0=0.277×10-3，n=0.021，Δx=7 467 m，Δt=1 h。

4 结果与分析

4.1 汇流演算方法参数分析

根据沅陵站实测流量数据，利用MC演算法和MCT可变参数法计算，模拟得到王家河站的出流数据。选取模拟的末时段，分析两种方法中的库朗数和雷诺数在15个河段上的变化过程，以19830710号洪水过程为例，其中参数沿河段的变化曲线见图3。

图3 两种汇流演算方法参数变化过程Fig.3 Parameter change process of two channel flow calculation methods for the confluence calculation

分段马斯京根法的参数k和ε在每个分段河道中不产生变化，属于线性参数。MC演算法和MCT可变参数法的演算参数与每个分段河道的参比流量Q有关。根据图3可知，两种方法的C和D沿河段呈曲线变化，属于非线性参数。

4.2 河道蓄量变化结果

对于一场洪水的模拟，通常更关注模拟过程线的洪峰、洪量、峰现时间与实际洪水过程的误差关系，实际上洪水的蓄量守恒状态也对模拟效果起着一定的作用。以式(7)计算河段的蓄量变化过程。若模拟的过程线蓄量在涨落后不守恒，则必然对模拟精度存在一定程度的偏差。在保证分段马斯京根法、MC演算法和MCT可变参数法3种方法模拟的起涨流量和完全退洪时的流量一致后，对率定期和验证期的洪水模拟结果计算蓄量守恒误差：

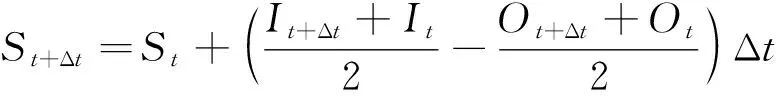
(7)

15场洪水中选取4场洪水计算汇流过程中河段蓄量的变化过程值。图4和表1分别为分段马斯京根法、MC演算法和MCT可变参数法模拟后河段蓄量的变化过程和蓄量相对误差。实际模拟过程中MC演算法的蓄量变化值证明了MC演算法的蓄量不守恒。观察3种方法在图4的始末位置情况，可以发现MC演算法相较于另外两种方法，在洪水结束时的河道蓄量值明显高于初始值。由表1可以得到，MC演算法的蓄量相对误差较大，最大误差值仅略低于45%；MCT可变参数法的蓄量误差很小，分析其原因可能为在实际计算过程中分段参数的舍入误差。分段马斯京根法由于汇流参数为恒定值，所以始末蓄量始终一致。

图4 蓄量变化过程Fig.4 Change process diagram of storage volume

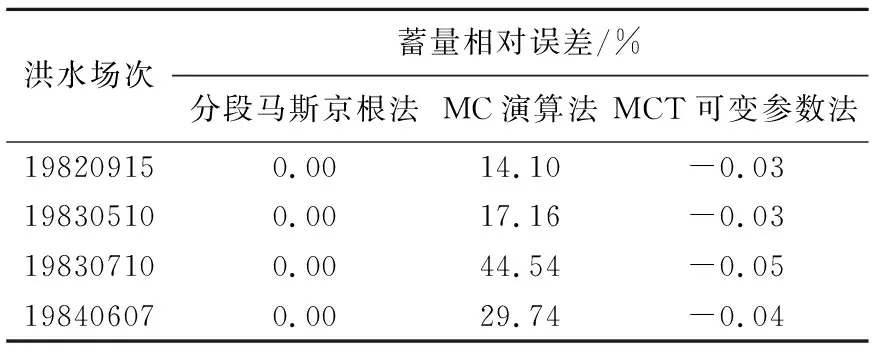
表1 蓄量相对误差

4.3 总体模拟结果分析

分段马斯京根法、MC演算法和MCT可变参数法3种方法河道汇流模拟结果见表2。选取洪峰相对误差、洪量相对误差、峰现时间误差和确定性系数4个指标对模拟效果进行评价。图5为3种方法在沅陵站—王家河站河段率定期和验证期的总体模拟精度情况(图中M、MC、MCT分别代表分段马斯京根法、MC演算法和MCT可变参数法)。图6为沅陵站—王家河站河段19820915号、19830510号、19830710号和19840607号洪水用3种方法得到的模拟流量过程线。

表2 3种方法河道汇流模拟结果

图5 沅陵站—王家河站河段洪水模拟精度箱线图Fig.5 Box plot of flood simulation accuracy in Yuanling-Wangjiahe channel section

图6 沅陵站—王家河站洪水模拟过程线Fig.6 Observed and simulated flood hydrographs in Yuanling-Wangjiahe reach

4.3.1 率定期结果分析

率定期共有9场洪水，从表2可以得到分段马斯京根法、MC演算法和MCT可变参数法的洪峰和洪量合格率均为100%，分段马斯京根法的峰现时间合格率为77.8%，MC演算法和MCT可变参数法的峰现时间合格率均为88.9%。分段马斯京根法、MC演算法和MCT可变参数法的确定性系数均值分别为0.870、0.889、0.891。

洪量误差方面，19790708号洪水、19800502号洪水、19820915号洪水在3种方法的模拟下洪量误差均超过-10%，其他场次洪量误差均在-10%以内；洪峰误差方面，MC演算法和MCT可变参数法有两场洪水洪峰误差超过-10%，分段马斯京根法只有一场超过-10%，分段马斯京根法表现更优；峰现时间误差方面，分段马斯京根法模拟19800518号洪水峰现时间误差较大，检查发现该洪水过程为多峰洪水，且两个峰值之间相隔时间较短，分段马斯京根法未模拟出实际最高的峰值，使得模拟峰现时间误差较大。除了该次洪水，只有一场洪水峰现时间误差超过10 h，3种方法很好地模拟了实际下游断面的峰现时间，说明分段马斯京根法、MC演算法、MCT可变参数法都很好地模拟出洪水在河道的扩散和传递。

4.3.2 验证期结果分析

验证期共有6场洪水，分段马斯京根法、MC演算法、MCT可变参数法的模拟精度结果见表2。3种方法的洪量合格率均为100%，只有19840606号洪水洪量误差超过-10%。分段马斯京根法的洪峰合格率为83.3%，MC演算法和MCT可变参数法的洪峰合格率略低，均为66.7%。19840606号洪水和19850703号洪水洪峰误差相对较大，其中19840606号洪水为多峰洪水过程，3种方法在第1个洪峰处模拟较好，但在第2个洪峰处，王家河站出流量远大于沅陵站入流量，分析其原因可能为该时段流域内降水量较大，区间入流增大。峰现时间误差均控制在10 h以内，模拟结果较好。除去19840606号洪水外，分段马斯京根法、MC演算法和MCT可变参数法的确定性系数均超过了0.9。

率定期的9场洪水对汇流参数进行了很好的率定，使得率定期和验证期次洪模拟达到了较好的精度。从图6可以看到分段马斯京根法、MC演算法、MCT可变参数法的模拟过程线与实测比较接近，对于多峰洪水的模拟效果也比较好。

总体上看，分段马斯京根法、MC演算法、MCT可变参数法模拟结果均比较理想。在模拟过程中，没有考虑旁侧入流，实际结果也反映出这个假设基本正确。由于MC演算法蓄量不守恒的问题，其最直接的影响是洪量模拟精度。从表2可以发现，除了19840430号洪水MC演算法的洪量模拟误差低于分段马斯京根法外，其余场次洪水洪量相对误差均最高，印证了蓄量不守恒会增加洪量误差的结论。从图5可见，MC演算法和MCT可变参数法的确定性系数相对分段马斯京根法精度更高且更为稳定。

5 结 论

a.MC演算法和MCT可变参数法基于运动波方程差分解的数值扩散在一定条件下模拟扩散波的物理扩散，能够反映天然河道中洪水波既传播又扩散的运动规律，在实际模拟过程中考虑河道断面形状和水力特性，贴近实际河道，对流域内宽浅河道的大中型洪水模拟效果较好。

b.MCT可变参数法在MC演算法的基础上加入了校正系数，增强了参数的时变性，解决了蓄量和稳态不一致的问题，在有限的范围内进一步提高了MC演算法的稳定性和模拟精度。

c.在河道断面相差不大的河段中，以断面参数平均值作为整个河段的概化形状，结果表明模拟精度较为满意，具有一定的可行性。

d.总体上看，分段马斯京根法、MC演算法、MCT可变参数法在沅陵站—王家河站河段的模拟结果较好。多数洪水均为多峰洪峰，次洪中存在多个流量涨落过程，且涨落较快，3种方法对于该类洪水也具有较强的适应性和可靠性。分段马斯京根法简便的计算步骤仍然可以带来良好的模拟效果。在实际模拟中，MC演算法和MCT可变参数法与分段马斯京根法取得的效果不相上下，甚至更优。