基于曲线特性的既有铁路整正研究
韩玉龙 孙海丽 丁志刚 贾庆鲁
(1.首都师范大学三维空间信息获取与应用教育部重点实验室,北京 100048;2.山东北斗华宸导航技术股份有限公司,山东淄博 255000)
截至2021年12月,我国铁路营业里程达到15万km。为保障列车运行的安全平稳,以及乘客乘坐的舒适性,必须保证铁路轨道的高平顺性[1-2]。
传统的铁路轨道平顺性调整方案,通常使用全站仪、水准仪、道尺、弦线等仪器测量轨道的几何状态,再由内业人员计算调整量,使之满足轨道平顺性指标限差[3-6]。由于列车对轨道的冲击,以及维护调整、地面沉降等原因,会使轨道实际中心线产生偏移现象[7],这给轨道平顺性调整带来很大困难。因此,根据实测线路拟合出满足要求的设计数据并计算调整量,对长期运营铁路平顺性测量与调整量计算具有重要意义。
目前,既有线路优化及调整多以高速铁路无砟轨道为研究对象,对有砟轨道养护维修作业研究较少。有砟铁路传统的维护措施,由于缺乏精确的设计线路及调整方案的支持,会导致长距离平顺性控制和整体线形几何参数恢复都达不到理想效果。
在既有线路平顺性调整中,李红艳等提出了既有铁路轨道线形及捣固方案优化技术,基于绝对测量数据计算轨道线形,并在此基础上进行捣固调整[8];张震等基于实测线形生成贴合实际线形的模拟设计线形,并以此为基础进行调整[9]。在轨道捣固质量控制方面,杨飞等通过研究轨道状态识别方法及控制标准,提出引入作业管理指标来辅助控制大机捣固质量[10];张皓然等通过对捣固前后线路质量进行多维度评估,针对捣固作业后的轨道几何形位的变化,提出了一套考虑波长因素的捣固方案[11]。
在以上研究的基础上,提出一种基于曲线特性的既有线路整正研究方法,根据实测数据对既有线路进行分析,拟合生成与实际位置偏差小、符合轨道曲线几何特性的模拟设计数据,以解决既有线路整正问题。
1 轨道设计数据线形特性
为保障铁路运行的安全性,提高旅客乘坐舒适度,轨道线路平、纵断面设计应满足一定的数学特性,以实现线路空间曲线的平顺性。轨道设计数据主要包括平曲线、竖曲线。
1.1 平曲线
铁路水平线形主要由平曲线体现。一般包括直线段、缓和曲线段和圆曲线段,缓和曲线一般用于连接直线段和圆曲线段,起到线路转角平稳过渡的作用。水平线形主要包括直缓点(ZH)、缓直点(HZ)、缓圆点(HY)、圆缓点(YH),将线形整体划分为直线段、缓和曲线、圆曲线。
平曲线设计数据主要由里程值、桩点X坐标、桩点Y坐标、桩点类型、切线方位角、圆曲线半径、超高等因素组成[12]。水平设计线形一般满足以下几何特征:直线的曲率恒定为0,圆曲线的曲率与设计半径R满足K=1/R。
圆曲线段长度与角度关系为
L圆=Δθ1×r
(1)
式中,L圆为圆曲线长度;Δθ1为圆曲线转弯角度;r为圆曲线半径。
缓和曲线是圆曲线与直线段之间的过渡曲线。在铁路从直线轨道驶入圆弧轨道的过程中起到缓冲作用,保障运行的安全平稳。缓和曲线满足任意点的曲率半径与缓和曲线起点的距离乘积保持不变的特性,即RL=A2(A2为常数)。其中,L为该点距缓和曲线起点的里程;缓和曲线曲率保持K=1/R=L/A2。因此,缓和曲线的曲率K是里程L的函数,即K=f(L)[13]。
缓和曲线段的转折角与缓和曲线段长度关系公式为
L缓=2×Δθ2×r
(2)
式中,L圆为缓和曲线长度;Δθ2为缓和曲线转弯角度;r为缓和曲线所连接圆曲线的半径。
1.2 竖曲线
竖曲线是把纵断面上两条相邻的纵坡线相交的转折点连接起来的一段曲线,主要为了对变坡点处列车竖直方向的冲击作用进行缓和。竖曲线中没有缓和曲线部分,直线段直接与圆曲线相连。根据变坡点在整体曲线上的位置,竖曲线可以分为凹曲线和凸曲线。凸曲线中变坡点在整体曲线上方,而凹曲线变坡点在整体曲线下方。
2 轨道平顺性理论
2.1 平面平顺性
平面平顺性主要是分析轨向方面,是指轨道中心线在水平面上的平顺性指标。轨向不平顺在直线段主要表现为不够笔直,曲线段具体表现为不够圆顺。当轨道平顺性达不到规范要求时,列车在行驶过程中就会出现较大的横向运动,甚至引起蛇形运动,会威胁到行车安全以及平稳。
参考《高速铁路工程测量规范》,轨道的轨向和高低测量要求计算3种不平顺值,即短波、中波、长波不平顺。短波以10 m弦线为基线,中波以30 m弦线基线,每隔5 m计算一次;长波以300 m弦线基线,每隔150 m计算一次。根据工程要求,以10 m弦短波不平顺为例进行分析。
轨道短波不平顺检测方法是以10 m弦线为基线,计算5 m处实测正矢与设计正矢之间的差值作为轨道平顺性的评价标准,短波平顺性检测方法公式为
Δh=|h设计-h实测|
(3)
式中,h设计为检测轨枕处设计正矢;h实测为检测轨枕处实测正矢。10 m弦短波不平顺检测方法示意见图1,其中,N为检测弦的起始位置。高低和轨向不平顺计算方法与之类似。
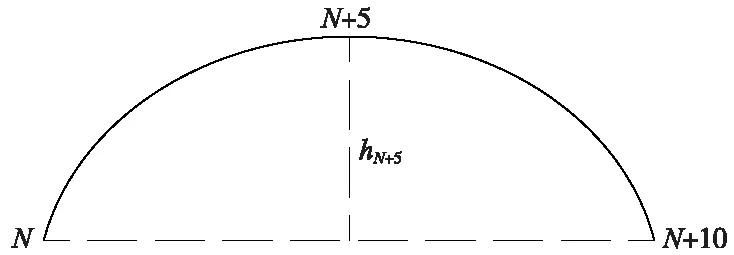
图1 10 m弦短波不平顺检测方法示意
2.2 竖向平顺性
高低是指轨道钢轨在竖直方向的平顺性指标,主要为防止钢轨存在高低不平的问题。由于地面沉降,扣件的松动以及列车行驶过程中的磨损等问题,高低不平顺难以避免。高低不平顺会造成列车在行驶过程中由于前后高低不平而产生冲击力较大的情况,会发生点头和振动,从而破坏轨道的高低平顺度,甚至会发生脱轨现象。
3 轨道平顺性调整方法
3.1 曲线约束下的线形计算
由于列车冲击,以及维护调整、地面沉降等原因,会使长期运营线路轨道实际中心线产生偏移现象,从而影响行车安全。根据实测数据对既有线路进行分析,拟合出即与实际位置偏差较小,又符合轨道曲线几何特性的模拟设计数据,能以较小的调整量使既有线路重新保持平顺。同时模拟设计线形可以固定作为目标线形进行多次调整,并最终使实际线路与之完全符合。
由于缓和曲线两端桩点位置曲率变化较小,只依靠线形拟合难以较为准确地确定直缓点与缓圆点,从而导致难以控制偏差计算结果。首先采用最小二乘法拟合计算直线参数;曲线段拟合获得圆曲线半径并根据曲率计算缓和曲线;最终通过桩点解算的方式反算模拟设计线形。
(1)线形计算
①直线段
选取明显位于直线段内的测量点利用最小二乘法进行拟合[14],得到直线方程,并确定线形参数,公式为
y=kx+b
(4)
式中,斜率为k;斜距为b。则可获得直线方位角αl=tan(k),以及曲线部分转折角β=α1-α2。
②曲线段
选取明显位于圆曲线段内的部分测量点,使用Taubin拟合理论[15]计算圆曲线方程,公式为
(x-a)2+(y-b)2=R2
(5)
由于缓和曲线两端桩点位置曲率变化较小,难以区分,采用曲率计算的方式进行解算。直线段曲率K=0;圆曲线的曲率为圆半径的倒数,即K=1/R;缓和曲线中曲率半径R与距起点里程L与保持RL=A2,即K=1/R=L/A2,因此缓和曲线曲率K与里程L为一次函数关系,在里程-曲率关系上表现为斜率不为0的直线,见图2。
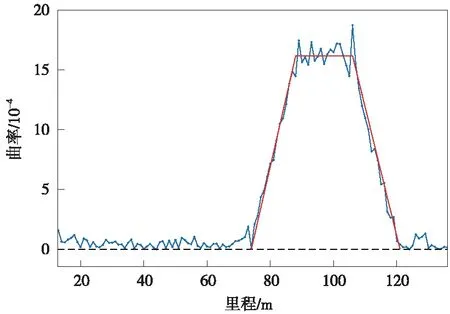
图2 里程-曲率关系
对轨道中心线实测数据求导,则各处曲率为
(6)
根据里程L和曲率K拟合参数A2,根据圆曲线曲率和A2,即可解算缓和曲线长度Lh。
由于曲线部分主要为两端直线之间的过渡连接部分,故曲线所提供转折角必须等于两段直线转折角,即β=γc+2γh。根据拟合获取的关键参数,圆曲线半径R、缓和曲线长度Lh,即可由曲线特性计算得缓和曲线转折角和圆曲线长度,有
(7)
Lc=γcR
(2)桩点解算
曲线部分缓和曲线里程增加为Lh,起始方位角等于前段直线方位角即αh=α1,圆半径为R,根据缓和曲线桩点计算公式,可得曲线切线增长和外矢距,有
(8)
式中,Hhx为曲线切线增长值;Hhy为外矢距。根据缓和曲线开始方位角,可计算x,y方向增量dhx1和dhy1。
根据圆曲线桩点计算公式,可得切线增长和外矢距,有
Hcx=Rsin(αc)
(9)
Hcy=R(1-cos(αc)
式中,Hcx为切线增长量;Hcy为外矢距;αc为圆曲线起始方位角。即可得到圆曲线x,y方向增量dcx,dcy。
Dx,Dy为两段缓和曲线与圆曲线增量之和。此时,根据前后两端直线参数与增量变化值,有
(10)
联合计算可得桩点坐标,直缓点坐标为
(11)
ZHy=k1×ZHx+b1
缓圆点、圆缓点和缓直点坐标分别根据逐段变化求得。竖向线形计算与水平线形计算相似,不再赘述。
3.2 轨道平顺性调整方法
(1)多项式拟合理论
轨道平顺性调整量采用多项式拟合[16]的方法进行计算。多项式拟合是一种将误差的平方最小化并获取与数据的最佳匹配的函数,是一种经典的数学优化方法。假如已知数据点(xi,yi)(i=0,1,2,…,n),则求多项式函数公式为
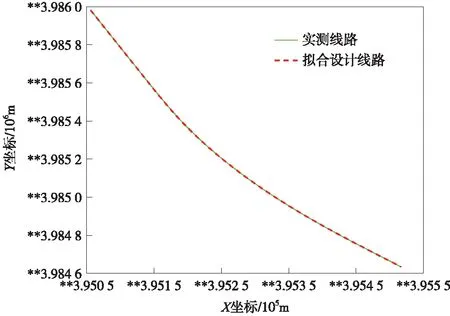
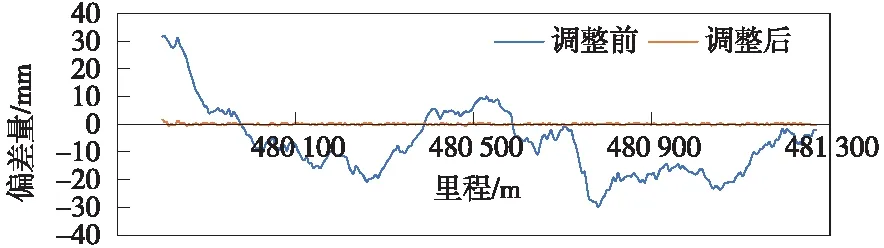
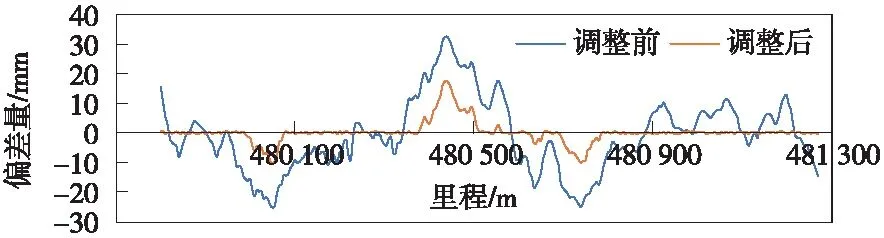
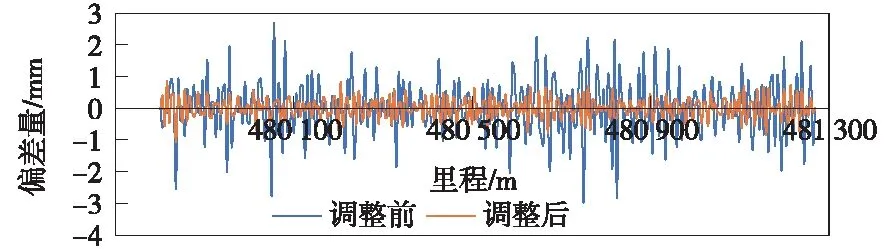
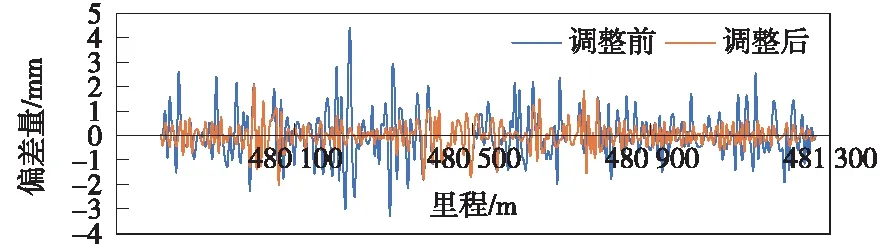
p(x)=a0+a1x+…+amxm(m+1 (12) 并使其满足 (13) 称为多项式拟合。参考聂松广无砟轨道基准轨模拟调整量自动计算方法研究成果[17],每分段中采用10阶多项式进行拟合。 (2)分段拟合方案 为使调整后线路尽量符合原设计,在以往调整方案的基础上,采取分段调整的方法;同时,为了保证整体的平顺前后各搭接30 m,首先将偏差量调整到合理范围,再进行多项式拟合。 平顺性调整中,首先根据设计数据和实测坐标再进行里程修正,将实测数据的里程归算至设计数据;对实测数据进行偏差计算,获得各测量点的横向偏差和垂向偏差数据。 各分段内部轨道平顺性调整,以线路绝对偏差的平方最小化作为优化目标函数,有 (14) 式中,xi为i点里程值;yi为此处偏差值;p(xi)为该点多项式拟合结果。 在目标函数的基础上,建立轨道各点调整量的约束条件。大机拨道作业的目标是使线路平面位置接近理想设计线形,然而受到复杂线路情况的干扰,以及机械设备自身调整范围的限制,调整效果很难达到预期目标。因此,需要建立轨道调整极限约束,即 (15) 式中,Ci为单i点轨道调整量;a,b分别为该点调整量的上限和下限。 首先根据偏差数据对轨道进行第一次调整,偏差量小于等于调整极限的,直接将偏差调整为0,即 Ci=-Di(i=0,1,2,…,n) (16) 式中,Ci为调整量;Di为偏差量。 偏差量大于调整极限时,令调整量为调整极限,即 Ci=Cmax(i=0,1,2,…,n) (17) 之后对轨道进行第二次调整,即将目标函数和约束不等式联合求解,获得轨道平顺性调整方案,实现了对轨道线形的调整和平顺性状态的控制。 在某普速铁路有砟轨道平顺性调整工程中,应用基于曲线特性的既有线路整正方法,生成模拟设计线形,并计算轨道调整方案,从而使其满足平顺性要求。测试线路长约2 km,包括直线段和曲线段。 测试过程中,首先使用轨道测量小车采集测试轨道左右轨及中线坐标、轨距、航向角、横滚角、俯仰角等数据;再根据线形计算和桩点解算测试区段线路的设计线形,并根据轨道平顺性调整方法生成轨道平顺性调整方案;最后将调整方案导入捣固大机,并进行平顺性调整。轨道测量小车主要集成了GNSS/IMU组合导航系统,并搭载了3个GNSS接收器、高性能惯导及里程计等,可融合GNSS基准站观测数据,解算轨道线路绝对坐标。在实际轨道平顺性调整工程中,其轨道横向偏差精度2 mm,垂向偏差测量精度2 mm,变形点水平方向精度1 mm,垂直方向精度1.5 mm,普速铁路轨道数据采集现场见图3。 图3 普速铁路轨道数据采集现场 本次平顺性调整主要应用对象为普速铁路有砟轨道,调整中主要根据基准轨调整绝对偏差,非基准轨及超高、轨距等由导轨调整车自动调整。具体调整方案中,先使用实测轨道中心线解算模拟设计数据,再根据模拟设计数据对轨道线路进行平顺性检测和调整。实测线路与拟合设计线路对比见图4,可以看出,拟合线路在保证线路符合轨道曲线几何规律的同时,与实测线路整体吻合较好。 图4 实测线路与拟合设计线路对比 对轨检小车采集的测量数据进行轨道调整量自动计算中,受限于普速铁路导轨调整车横向调整极限±30 mm,垂向调整0~30 mm,垂向调整中首先以±15 mm为极限,最后做整体抬升调整。误差在调整极限内的首先将误差调为0,再进行平顺性调整。轨道平顺性调整前后横向偏差见图5,轨道平顺性调整前后垂向偏差见图6。 图5 轨道平顺性调整前后横向偏差 图6 轨道平顺性调整前后垂向偏差 本次实测线路为时速小于160 km的普速铁路,轨向限差1.4 mm,高低限差为1.8 mm。调整前后轨向不平顺对比见图7、图8。不难看出,调整后轨向不平顺和高低不平顺整体大幅降低(见表1、表2)。最终调整后,TQI合格率为100%,符合线路养护维修作业验收要求。 表1 轨向合格率对比 表2 高低合格率对比 图7 调整前后轨向不平顺对比 图8 调整前后高低不平顺对比 受限于导轨车调整极限,实际线形无法通过一次调整到位。模拟设计线形可以固定,作为目标线形进行多次调整,并最终使实际线路与之完全符合。 对于长期运营线路轨道实际中心线产生偏移的现象,研究一种基于曲线特性的既有线路整正方法。根据实测数据对既有线路进行分析,并拟合出与实际位置偏差较小,又符合轨道曲线几何特性的模拟设计数据,以较小的调整量使既有线路重新保持平顺,并且在长期的运营维护中可以将其固定作为目标线形。在实际工程中,对前述方法进行了应用,并针对工程需求提出轨道平顺性分段调整的方案。在实际工程中对两种方案进行实验验证,效果良好。4 应用测试



5 结语

