基于遗传算法的铝合金斩波盘等强度优化设计

鲍明森，龚海，张涛，余周香，刘晓龙

(1.中南大学 轻合金研究院，湖南 长沙，410083；2.高性能复杂制造国家重点实验室，湖南 长沙，410083；3.中国原子能科学研究院 核物理研究所，北京 102413)

高通量反应堆中子源产生的是稳态连续中子束流，为有效截取所需波长的中子，有的中子谱仪使用单色器，也有的谱仪使用中子斩波器(中子飞行时间谱仪)[1-2]。中子斩波器是中子飞行时间谱仪必不可少的关键设备，可用于中子波段范围选择、脉冲化、单色、周期交叠抑制等[3-4]。转盘式斩波器是中子斩波器最常用的形式[5]，绕平行于中子束的轴高速旋转，将连续中子束切割为一系列宽度相等的中子脉冲束(脉冲化功能)[6-8]。随着对中子飞行时间谱仪性能的要求不断提高，需要使斩波盘转速能够达到20 000 r/min 甚至更高[9-10]，但斩波盘在高速旋转情况下会产生较大的离心力，当离心力过大时，其内部应力超过屈服强度，发生塑性变形[11]。故对斩波盘进行优化设计是很有必要的。JAFARI 等[12]通过模拟退火和粒子群优化等现代优化方法，以Mises 屈服准则作为约束条件，对变厚度转盘质量进行了最优设计。KHORSAND等[13]采用混沌粒子群优化方法对转盘形状进行优化，从而减小转盘的应力及位移。曹淼龙等[14]提出了基于STEP/SDAI的转盘优化设计，合理优化转盘轮廓线，提高了应力分布均匀性。GUTZWILLER 等[15]利用遗传算法对涡轮机械盘形状进行优化，实现了快速低保真度设计。PÜHLHOFER 等[10]使用高比强度的CFRP(carbon fiber reinforced plastics)作为斩波盘材料，进行了斩波盘的设计、制造和测试。WEINZIERL等[16]通过数值优化来改进斩波盘，优化槽口形状，提高斩波盘最大旋转速度。ANTONELLI 等[17]基于Grammel准则，对变厚度高速旋转圆盘进行了等强度设计。尽管CFRP是一种轻质坚固的材料，但存在各向异性、加工工艺复杂、经济成本高等缺点；而铝合金具有各向同性、易加工、成本低等优点，故本文选择铝合金作为斩波盘材料。铝合金斩波盘存在以下2 个问题：高速旋转的斩波盘应力较大，易发生变形失效；斩波盘槽口存在应力集中[11]。本文对等厚度和某型号变厚度斩波盘(阶梯变化)在20 000 r/min转速下的工作过程进行有限元仿真，并对二者的应力场进行分析；基于理论计算和遗传算法，提出一种新的变厚度轮廓曲线，实现连续变厚度转盘(无槽口)等强度优化设计，减小斩波盘应力，提高应力分布均匀性；通过有限元模拟，对U 形槽口进行局部加厚及增大圆角半径，有效解决槽口应力集中问题；对优化后的斩波盘在20 000 r/min 及更高转速下的工作过程进行有限元仿真，研究优化后斩波盘的最高转速。

1 传统斩波盘受力分析

1.1 斩波盘介绍

连续波长的中子束通过高速旋转的斩波盘，被切割为宽度相等的中子脉冲束，使探测器所需波段的中子无损失通过，如图1所示。斩波盘在高速旋转过程中会承受极大离心力，若斩波盘材质强度偏低，则工作过程中易变形失效。7050 铝合金具有密度低、强度高、热加工性能好等优点，在航空航天结构件上得到广泛应用[18-19]，因此，本文选择7050 铝合金作为斩波盘材料，其材料参数如表1所示。

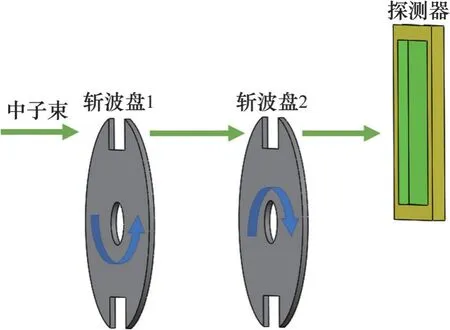
图1 斩波盘工作示意图Fig.1 Schematic diagram of chopper disc operation

表1 7050铝合金材料参数Table 1 Material parameters of 7050 aluminum alloy

斩波盘的典型外径为500～800 mm，具有不同数量的槽口。本文以某型号斩波盘为基础，其直径为700 mm，中心孔半径为39 mm，共有14 个U形槽口，如图2所示。

图2 斩波盘平面图Fig.2 Floor plan of chopper disc

1.2 等厚度斩波盘受力分析

通过Abaqus 有限元软件对等厚度斩波盘在20 000 r/min 转速下的受力情况进行仿真。在仿真过程中，载荷与边界条件是2个重要因素，其中载荷类型选为“旋转体力”，角速度为2 095 rad/s；并将中心孔内表面进行完全约束(图3(a))。

仿真结果如图3(b)所示。等厚度斩波盘中间部位的Mises应力达到屈服强度，发生塑性变形，因此，以7050 铝合金为材质的等厚度转盘无法满足20 000 r/min的工作要求。

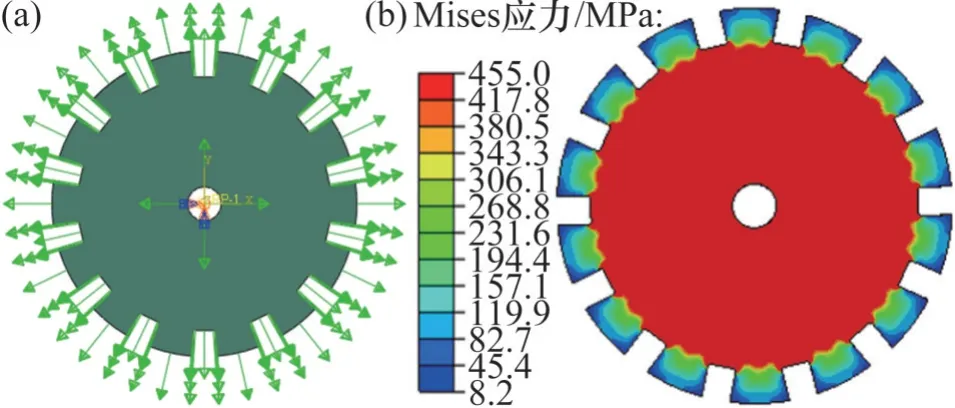
图3 等厚度斩波盘有限元分析Fig.3 Finite element analysis of chopper disc with equal thickness

1.3 变厚度斩波盘受力分析

针对等厚度转盘应力过大情况，采用某型号阶梯变化的变厚度转盘，其内圈半径仍为39 mm，外圈半径为350 mm，厚度由转盘的中心到外圈逐渐减小，如表2所示。

根据表2 中数据，对该转盘在20 000 r/min 转速下的工作过程进行有限元仿真，结果如图4 所示。从图4可见：变厚度转盘在槽口底部出现应力集中情况，最大Mises应力为455.95 MPa，表明该变厚度转盘在槽口底部发生塑性变形。为精确分析转盘的应力分布情况，在转盘上取如图4所示的路径Path-1，其应力变化如图5所示。从图5可见：转盘中心孔Mises 应力较大，为302 MPa；在径向45～270 mm范围内，平均应力为252 MPa，应力变化范围为(252±30) MPa；之后应力逐渐减小，在350 mm处达到最小，为42 MPa。

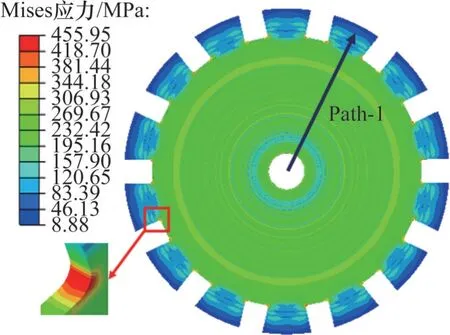
图4 变厚度斩波盘Mises应力云图Fig.4 Mises stress nephogram of chopper disc with variable thickness

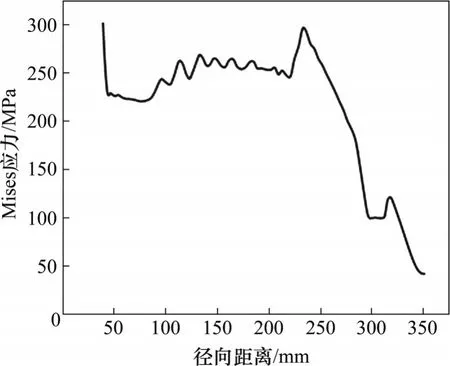
图5 变厚度斩波盘Mises应力Fig.5 Mises stress of chopper disc with variable thickness

表2 某型号变厚度转盘参数Table 2 Parameters of a disc with variable thickness

1.4 变厚度斩波盘受力定性分析

呈阶梯变化的变厚度斩波盘应力变化趋势呈锯齿形波动，且与等厚度斩波盘相比应力明显减小。

变厚度斩波盘受力定性分析结果如图6 所示。图6(a)中，等厚度单元体圆心角为θ，厚度为t，以转速ω绕中心轴匀速旋转，质量为m。

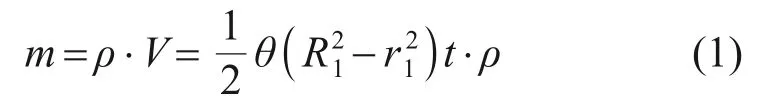
式中：ρ为7050 铝合金密度，t/mm3；R1为外径，mm；r1为内径，mm。

等厚度单元体在截面P上的应力为

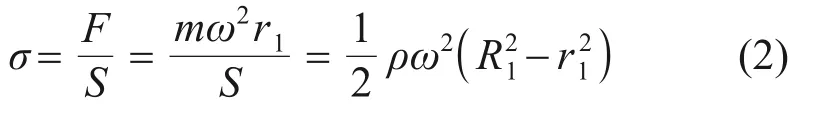
式中：σ为应力，MPa；F为载荷，N；S为截面P的面积，mm2：

由式(2)可知，在同一厚度层内，应力随径向距离r1的增大而减小；在阶梯位置，厚度变小，使得截面P 的面积减小，引起阶梯处应力发生突变，应力变化趋势由减小转变为增大。阶梯变化的变厚度转盘在高速旋转时，出现如图5所示的锯齿形波动。

变厚度斩波盘受力定性分析结果如图6 所示。从图6(b)可见：当变厚度斩波盘由等厚度转变为变厚度时，其质量减小至m-m1，即在等厚度的基础上去除质量为m1的部分。由式(2)可知，当截面积S不变而质量减小时，应力减小。因此，由等厚度转为变厚度后，截面P上的应力减小。

图6 变厚度斩波盘受力定性分析Fig.6 Qualitative analysis of force of chopper disc with variable thickness

尽管阶梯变化的变厚度斩波盘应力相较于等厚度斩波盘应力明显减小，但仍有不足之处。阶梯变化的斩波盘在20 000 r/min 转速下，整体平均应力及应力变化波动大，中心孔与槽口底部存在应力集中现象。因此，需要通过对斩波盘进行合理的连续变厚度设计，以减小斩波盘应力，提高应力分布均匀性。

2 斩波盘优化设计

2.1 变厚度转盘形状优化理论

为优化转盘的形状，首先需要推导计算出轮廓曲线为H(r)情况下的径向应力σr和周向应力σθ，最后计算转盘的Mises 等效应力σi。通过对轮廓曲线H(r)不断优化，从而得到最优的变厚度转盘形状。

尽管斩波盘外围存在等间距分布的U形槽口，但这些槽口对斩波盘整体应力影响有限，因此，将其视为规则的变厚度转盘进行设计。变厚度转盘示意图如图7所示。变厚度转盘围绕中心轴作匀速圆周运动，转速为ω，转盘内半径为a，外半径为b。转盘在转动过程中由于离心力的存在会产生内应力，在旋转体力fr的作用下处于平衡状态。

图7 变厚度转盘Fig.7 Disc with variable thickness

由弹塑性力学相关理论，可以得到关于位移分量u的微分方程[20-21]：

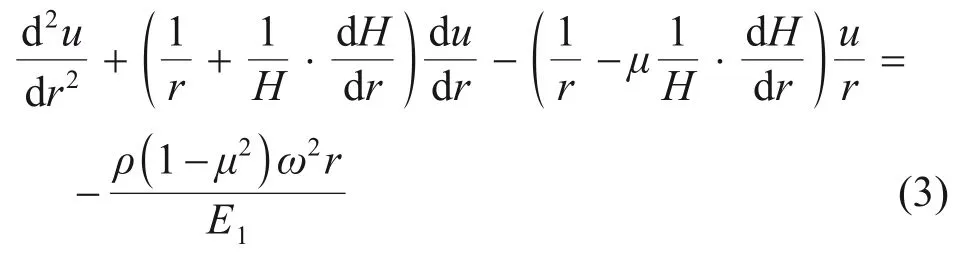
式中：H为转盘轮廓曲线函数；u为位移函数；E1为材料弹性模量；μ为泊松比；r为径向距离(与转盘中心轴的距离)，mm。该微分方程有以下2个边界条件：

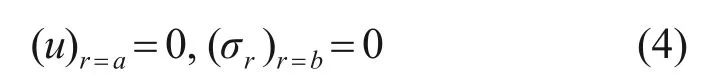
当轮廓曲线H(r)已知时，通过对微分方程(3)进行求解，得到位移函数u(r)，将求得的位移函数代入式(5)，可求得转盘的径向应力σr和环向应力σθ：

进而求得Mises等效应力 σi：

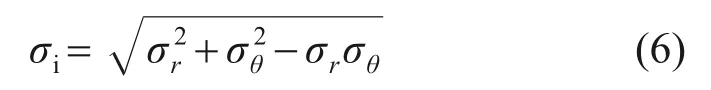
2.2 基于遗传算法的变厚度转盘等强度优化设计

2.2.1 优化参数的选择

在以往研究中，变厚度转盘的轮廓曲线一般选择为双曲线形式，但在优化过程中发现双曲线轮廓很难使转盘达到等强度状态，为此，本文提出一种新的变厚度轮廓曲线函数，如式(7)所示：

式(7)中右边前3项是一个标准的二次函数，后2项是指数函数。其中，二次函数项作为转盘厚度曲线的主体，决定了转盘厚度的主要变化趋势，将2个指数项作为微调项分别对转盘中心和外侧的厚度进行局部微调，三者共同作用，可以使转盘处于理想的等强度状态。

厚度变化函数H(r)存在5 个未知系数：A，B，C，D和E。其中，A，B，C作为二次函数的3 个系数，对厚度起主要作用。但在用遗传算法进行优化过程中，如果直接以系数A，B和C为设计变量，则很难得到合适的最优解。变厚度轮廓曲线二次函数项的插值点如图8所示。对于厚度变化曲线H(r)上i，j和k这3 点的纵坐标，A1，B1和C1为设计变量。通过对i，j和k这3 点进行二次插值计算出系数A，B和C，间接对系数进行优化。

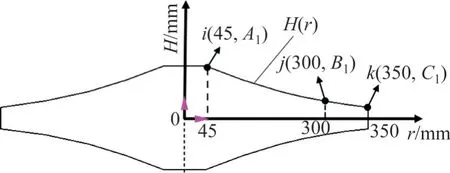
图8 变厚度转盘轮廓曲线二次函数项插值点Fig.8 Interpolation points of quadratic function terms of contour curves of variable thickness disc

由于斩波盘中心位置存在1个用于装夹固定的平台，因此，厚度变化曲线H(r)从距离中心45 mm处开始(径向39 mm 至45 mm 范围内为固定平台)。点i为曲线起始点，坐标设为(45，A1)；j距离中心轴300 mm，坐标设为(300，B1)；k为厚度变化曲线的终点，坐标设为(350，C1)。通过对A1，B1和C1的取值范围进行合理的初始化约束，使得它们只能在一个固定区间取值，从而使遗传算法的搜索范围受到限制，减小算法的工作量，最终可以快速得到理想的最优解。

其中，第1 个点i的纵坐标A1作为转盘的初始厚度(转盘关于X轴上下对称)，可以根据表2 中变厚度转盘，给出合理的约束范围：A1∈(7，15)。第3个点k的纵坐标C1作为边缘位置厚度，可以根据转盘的最小厚度对其进行约束。考虑到加工工艺，将转盘的最小厚度设为1.5 mm。此外，考虑到存在微调项，C1取值范围可以约束为：C1∈ (-1，1)。第二点j距离中心轴300 mm 处，该位置厚度可以借鉴第3个点k的纵坐标取值，故B1的取值范围可以约束为：B1∈ (-1，1)。

最后，微调项用于对二次函数进行局部微调整，其取值范围应控制在较小范围内，故D和E的取值范围可以约束为：D∈(-1，1)，E∈ (-1，1)。

2.2.2 参数优化

为合理评估转盘优化的效果，首先以已有的某型号变厚度转盘的应力和质量为基准(该转盘的平均应力为252 MPa、质量为6.8 kg，应力变化范围为±30 MPa)，对优化后的应力和质量进行量纲一处理，最后对量纲一参数进行加权。

为了减小斩波盘的平均应力，并提高应力分布均匀性，需要同时考虑质量，因此，对应力的权重取为0.8(其中平均应力和应力分布均匀性的权重各取0.4)，而质量的权重取0.2，则设计目标y为

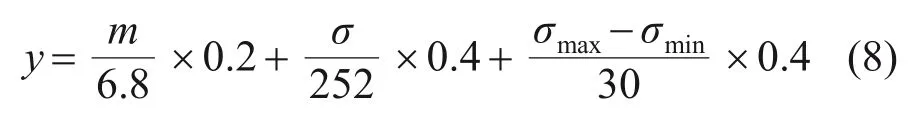
式中：σmax为最大Mises 应力，MPa；σmin为最小Mises 应力，MPa；σmax-σmin用于表征应力分布均匀性；σ为转盘平均Mises 应力，MPa；m为转盘的质量。

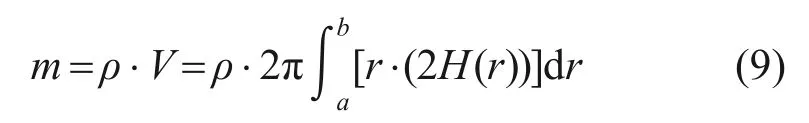
约束条件为：

1) 转盘各点的Mises 应力之差不超过15 MPa，转盘接近等强度状态，即

2) 转盘上各点等效应力Mises 需小于屈服强度，即

式中：σs为材料的屈服强度，MPa。

2.2.3 优化结果

以式(8)的设计目标y作为遗传算法的适应度，经过不断优化，得到如下结果：A1=13.443 7，B1=0.123 1，C1=-0.711 4，D=-0.172 5，E=-0.933。

利用二次插值可以计算得到：A=1.165 5×10-4，B=-0.092 4，C=17.367 8。代入式(7)可得轮廓曲线方程：

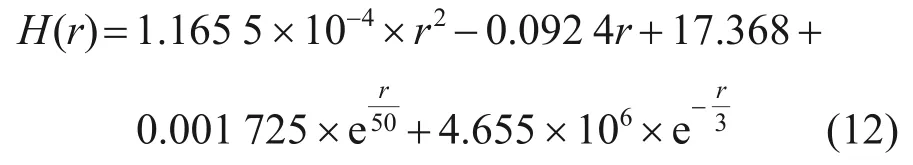
变厚度转盘轮廓曲线如图9所示，可见优化后转盘的厚度变化趋势为：从中心到外侧先减小后增大。由于转盘关于X轴上下对称，因此，中心位置最厚为14.87×2 mm，在径向距离(与转盘中心轴的距离)315 mm 处厚度达到最小(0.75×2 mm)；接着，厚度逐渐增大，在径向距离350 mm 处厚度为1.18×2 mm。

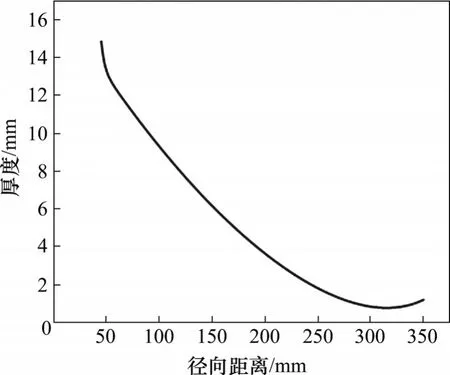
图9 变厚度转盘轮廓曲线Fig.9 Contour curve of variable thickness disc

通过理论计算，优化后的转盘在20 000 r/min转速下的受力情况如图10所示。从图10可见：转盘基本处于等强度状态，转盘中心孔位置最大Mises 应力为204 MPa，而转盘整体平均应力为197 MPa，应力变化范围为±7 MPa，表明变厚度转盘的等强度优化设计效果良好。

图10 变厚度转盘理论计算应力(无槽口)Fig.10 Calculated stress of variable thickness disc(no notch)

2.3 U形槽口局部优化

在等强度优化设计过程中，未考虑斩波盘的槽口。事实上，斩波盘在高速旋转过程中，槽口底部会出现如图4所示的应力集中情况，若不对其进行优化，则在工作过程中槽口底部结构将发生破坏。优化槽口的方法有很多，本文采用局部加厚与增大圆角半径相结合的方式，以减小槽口应力。

2.3.1 局部加厚机理

局部加厚机理分析如图11 所示。如图11(a)所示，厚度为h的单元体以转速ω绕中心轴匀速旋转，由式(2)可知，当截面积增大，而载荷不变或变化较小时，应力随之减小。而局部加厚的实质就是通过增加截面积，达到减小槽口处应力集中的效果。

由式(3)和式(5)可知，当转盘为等厚度盘时，厚度曲线H为常数，因此，等厚度盘的应力与厚度无关。如图11(b)所示，厚度为h的单元体通过整体加厚和局部加厚2 种方式进行加厚；当采用整体加厚时，单元体呈等厚度状态，因此，应力不变；而采用局部加厚时，单元体截面积增加，但所受载荷与整体加厚相比有所减小，因此，应力减小。

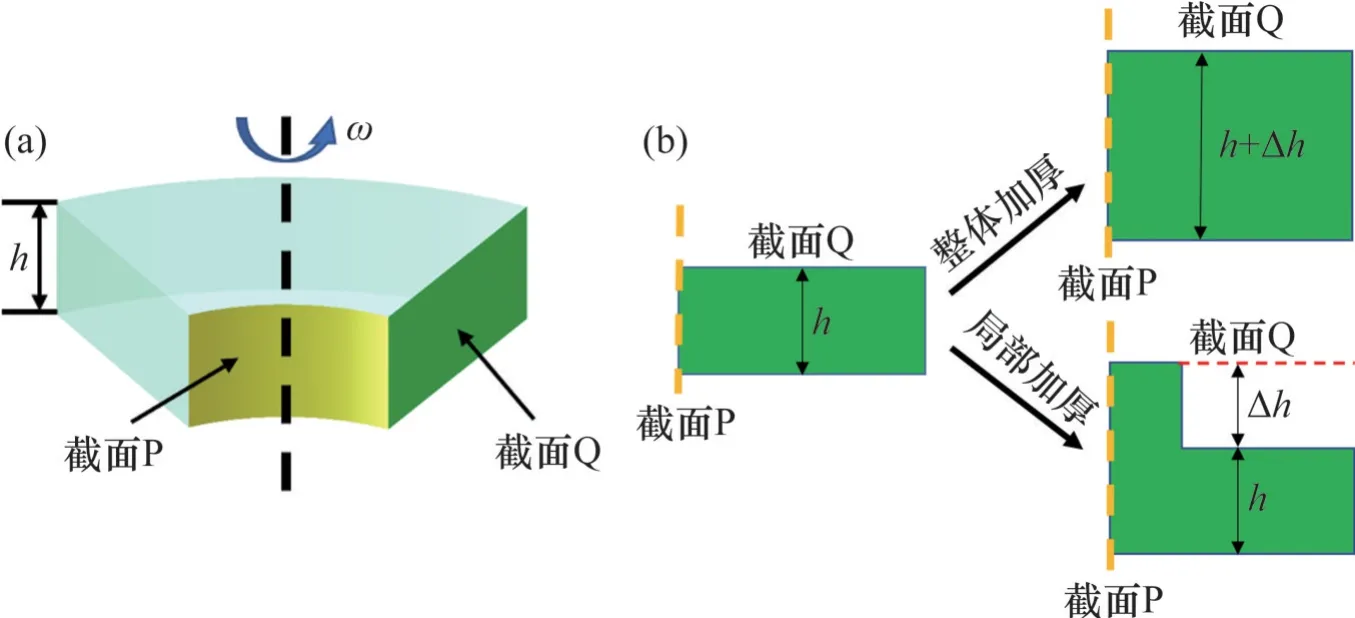
图11 局部加厚机理分析Fig.11 Mechanism analysis of local thickening

2.3.2 槽口优化措施

槽口局部厚度优化示意图如图12 所示。从图12(b)可见，M作为起始加厚位置，N作为结束加厚位置，厚度在N处开始减小。在仿真过程中发现，当所加厚度超过5 mm或从所加厚度直接减小至斩波盘原厚度时，N处会出现较大的应力集中，因此，在径向半径R为270～285 mm 时，将厚度增至5 mm；为避免厚度减小引起的应力集中现象，径向半径R为285～305 mm 时，厚度由5 mm 线性减小至斩波盘原厚度1.6 mm。此外，为进一步降低槽口的应力集中现象，在局部加厚的基础上适当扩大圆角半径R至20 mm(如图12(a)所示)。

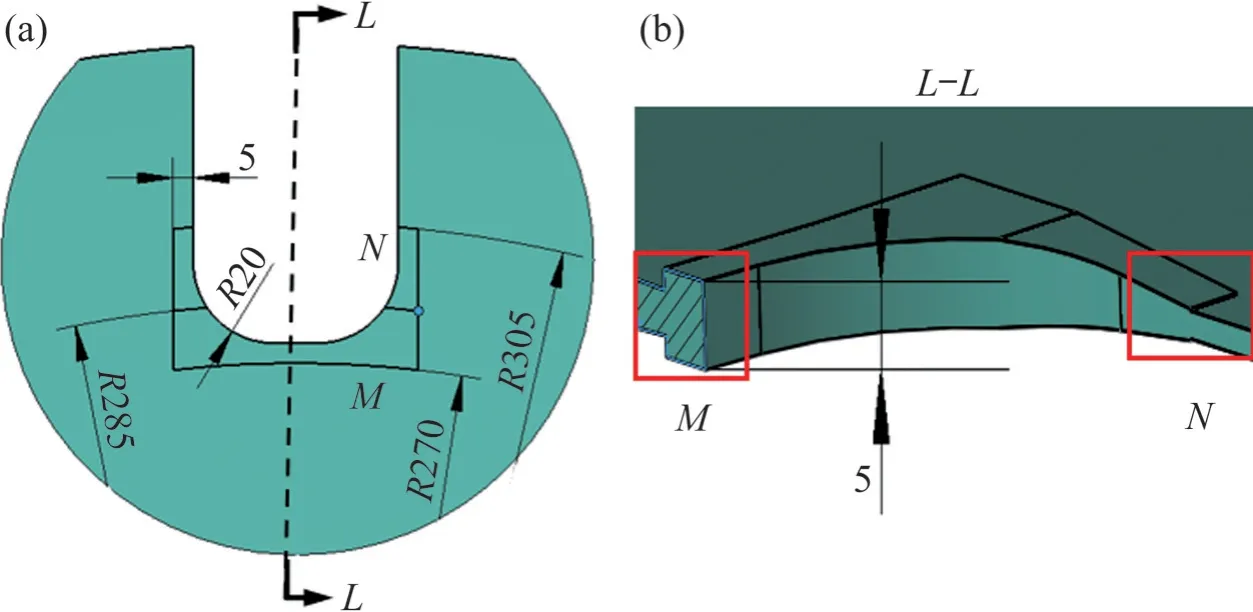
图12 槽口局部厚度优化Fig.12 Optimization of local thickness of notches

2.4 优化后斩波盘受力分析

经过等强度优化、槽口局部优化，分析斩波盘在20 000 r/min 转速下的受力情况，对其进行有限元仿真，得到如图13 所示的优化后斩波盘应力分布云图。从图13 可见：优化后的斩波盘在槽口底部最大Mises应力为271 MPa，相较于优化前(图4)，槽口应力减小40.4%。为精确分析优化后斩波盘的应力分布情况，取如图13 所示的路径Path-2，得到如图14所示的应力变化曲线。

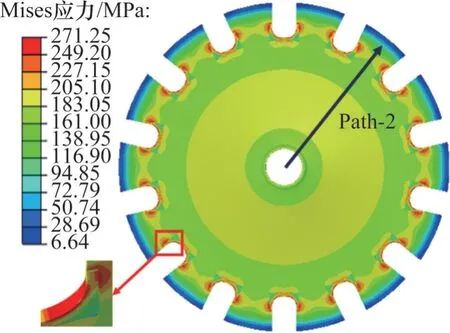
图13 优化后斩波盘Mises应力云图Fig.13 Mises stress nephogram of the optimized chopper disc

图14 Mises应力分布Fig.14 Distribution of Mises stress

由图14 可知：优化后斩波盘中心孔最大应力为200 MPa，在径向310 mm 之内，平均应力为182 MPa，应力变化范围为±6 MPa。与理论计算的应力相比，由于槽口存在，影响了斩波盘边缘应力场，使得斩波盘边缘应力下降明显，并使得斩波盘平均应力下降15 MPa，但应力有限元仿真结果仍与理论计算结果相符合，表明设计合理。

3 结果讨论

3.1 优化前后应力对比分析

优化前后应力对比如图15 所示。从图15 可见：通过优化前后斩波盘应力对比，发现优化后的斩波盘应力显著减小。优化前斩波盘在中心孔应力为302 MPa，而优化后斩波盘在中心孔应力为200 MPa，中心孔应力减小33.8%；其次，优化前的平均应力为252 MPa，而优化后斩波盘的平均应力为182 MPa，平均应力减小27.8%。

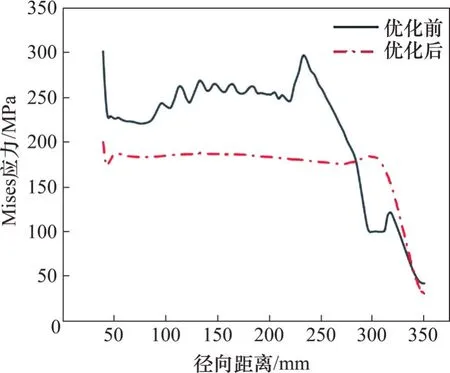
图15 优化前后应力对比Fig.15 Stress comparison before and after optimization

此外，优化后的斩波盘应力分布均匀性明显提高。由于优化前的斩波盘厚度呈阶梯变化，应力场在阶梯位置存在较大波动，使得应力分布均匀性较差。而优化后的斩波盘其厚度连续且合理变化，使得斩波盘的应力变化平缓、分布均匀。由图15 可知：优化前斩波盘的应力变化范围为(252±30) MPa，而优化后斩波盘的应力变化范围为(182±6) MPa，应力分布均匀性提高80%。

3.2 槽口应力与极限转速

由于U形槽口底部应力高于斩波盘平均应力，因此，斩波盘所能承受的极限转速主要受槽口应力限制，为探求优化后斩波盘的极限转速，分别在20 000，24 000，25 000和26 000 r/min这4种转速下对其进行受力分析，槽口应力分布情况如图16所示。

从图16(a)可见：斩波盘在20 000 r/min转速下槽口最大Mises应力为271 MPa，远低于屈服强度。由式(2)可知，当转速提高时，转盘内应力也随之增大，且转盘内应力与转速的平方呈正比，因此，当转速提升至24 000 r/min 时，槽口最大Mises 应力为390 MPa(如图16(b)所示)，此时，安全系数为455/390≈1.17；当转速提升至25 000 r/min 时，槽口最大Mises 应力为424 MPa(如图16(c)所示)，此时接近但仍小于屈服强度；当转速提升至26 000 r/min时，槽口最大Mises 应力为455 MPa(如图16(d)所示)，此时槽口发生塑性变形。因此，优化后斩波盘极限转速可达25 000 r/min。

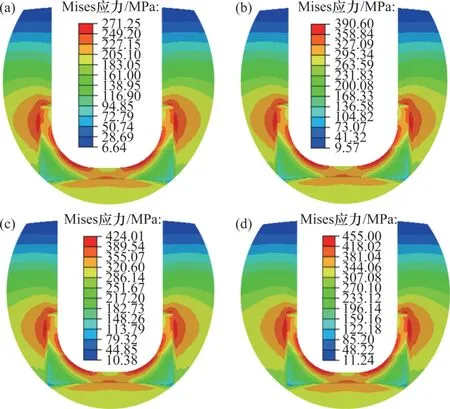
图16 不同转速下槽口应力Fig.16 Notch stress at different rotational speeds

3.3 能量分辨率

斩波盘型冷中子飞行时间谱仪通过改变斩波盘旋转频率来调整仪器分辨率[22]。通常用入射中子的弹性散射能量峰半宽度ΔEFWHM表征冷中子飞行时间谱仪的能量分辨率，具体表达式为

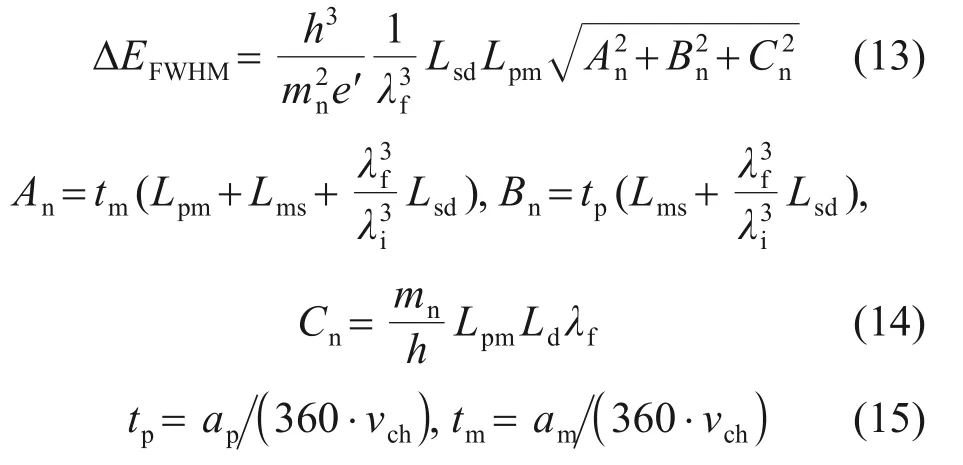
式中：h为普朗克常数；mn为中子质量；e′为基本电荷；Lsd为样探距；λi为入射中子波长；λf为散射中子波长；Lpm为第一个斩波盘和最后一个斩波盘的间距；Lms为最后一个斩波盘与样品之间的间距；ap为脉冲斩波器切口角度；am为单色斩波器切口角度；Ld为飞行距离误差；vch为斩波盘旋转频率。

取λf=λi，忽略小项Cn，则可近似得出

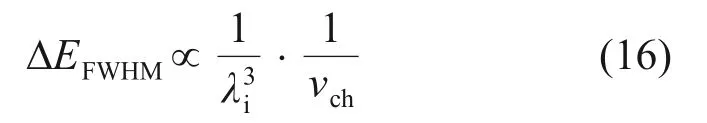
由式(16)可知：当λi不变时，增大斩波盘旋转频率vch能有效提高谱仪的能量分辨率。优化前的斩波盘无法满足20 000 r/min 的工作要求，而经过优化后的7050铝合金斩波盘在1.17倍安全系数下，最大转速可提升至24 000 r/min，因此，冷中子飞行时间谱仪的能量分辨率显著提高，适用于更高频率的材料微观动力学测量。

4 结论

1) 针对7050 材质铝合金斩波盘结构设计不合理、无法满足高速旋转的问题，提出了一种连续变厚度轮廓曲线，可实现斩波盘等强度优化设计，并通过局部尺寸优化可大幅度降低斩波盘槽口的应力集中现象。

2) 结构优化后的斩波盘平均应力明显减小，应力分布均匀性大幅度提高。在20 000 r/min 转速下，7050 铝合金斩波盘基本处于等强度状态，与优化前相比，斩波盘平均应力降低26.7%，应力分布均匀性提高85%。

3) 斩波盘中心孔应力及槽口底部应力大幅度减小。在20 000 r/min 转速下，与优化前相比，7050铝合金斩波盘中心孔应力降低33.8%，槽口应力降低40.4%。

4) 斩波盘的最高转速显著提升，冷中子飞行时间谱仪的能量分辨率显著提高，适用于更高频率的材料微观动力学测量。在屈服强度为455 MPa、安全系数为1.17 的基本条件下，优化后的7050 铝合金斩波盘最大许用转速可达24 000 r/min；当转速提升至25 000 r/min 时，槽口应力为424 MPa，接近屈服强度；当转速提升至26 000 r/min 时，槽口应力达到屈服强度，发生塑性变形。