PTFE材料正交切削切屑成形特性研究

倪 敬 孙静波 何利华 崔 智 薛 飞

1.杭州电子科技大学机械工程学院，杭州，310018 2.浙江启尔机电技术有限公司，杭州，310018

0 引言

聚四氟乙烯(polytetrafluoroethylene，PTFE)材料因优秀的自润滑性能和耐化学腐蚀性能而在半导体领域广泛应用[1]。结构简单的PTFE材料元件(如管道、棒材等)大都采用推压、模压、挤出等成形方法设计制造[2]，但结构复杂的PTFE材料元件(如泵和阀)则需要在上述成形方法的基础上进行二次切削加工。然而，王春震等[3]、王平等[4]、朱富军等[5]进行PTFE材料车削加工时发现，PTFE材料导热性差，弹性模量低，刚性较差却又有高弹性，这使机加零件难以保证较高的尺寸精度，材料去除并不均匀，而切屑的微观形貌可以反映材料去除过程中复杂的塑性变形和力学变化，所以研究不同切削参数条件下材料的切屑成形特性对理解和评估材料切削加工机理与切削加工性能有重要作用。

PTFE等聚合物材料在切削过程中的材料去除行为与金属不同,干式切削中，在切削力作用下，切屑断裂表面有“撕裂”现象出现[6]。AZMI[7]利用高速相机观察了纤维增强聚合物端铣过程中切屑沿着纤维取向的断裂过程。LI等[8]描述了正交切削UD-CFRP过程中的切屑形成特征，并揭示了切削深度对切屑形态的影响。ERENKOV[9]研究了热塑性塑料在切削过程中切削区的不均匀压缩变形和局部剪切变形，以及关节状切屑的形成原因。苑伟政等[10]观察非晶态聚合物动态切屑形成过程后指出，裂纹的扩展导致切屑的初始剥离。CARR等[11]对几种聚合物进行了单点金刚石加工，指出当剪切应力超过聚合物的剪切模式断裂时，裂纹形成并沿力矢量方向扩展。

在切屑成形机理的研究方法方面，WANG等[12]研究了塑性聚合物的切削机理，发现工-屑间是通过断裂分离的，之后又根据剪切平面理论，阐述了两种不同固化物固化后环氧树脂的切屑断裂与连续现象[13]。很多研究人员都认为断裂是材料去除的主导机制，认为切削过程中看不到明显的裂纹，是因为裂纹聚集于刀具刀尖处，裂纹的扩展与刀具进给方向保持一致[14-16]。LU等[17]基于未在刀具切削刃前发现可见裂纹这一观察结果，利用塑性流动理论来解释刀具切削刃周围的材料去除过程。

李强等[18]基于绝热剪切理论研究了DD5镍基单晶高温合金在高速铣削状态下切屑毛边的形成机理，并利用毛边定量结构评价方法探究了切屑毛边随着切削速度的形态变化。宁福达[19]、肖茂华[20]针对镍基高温合金高速铣削状态下的切屑毛边进行分析，发现切屑毛边高度和间距随着切削参数的变化有一定变化趋势，而且对切削力波动也有一定影响。周俊[21]对高速切削GH4169的切屑形态进行了机理分析，发现绝热剪切面上的应力分布和作用时间决定了裂纹扩展形态，从而形成切屑毛边。邹中妃[22]认为在切削GH4169时，刀具形状、切削速度对切屑毛边的形态都有一定影响。

以往研究多集中于金属以及纤维增强聚合物的成屑特性，但金属材料、纤维增强聚合物材料与高纯聚合物材料的去除过程有很大差异，关于高纯PTFE材料的成屑特性更是鲜有报道。本文通过单因素正交切削实验和准静态力学实验，探究了PTFE材料的切屑成形特性,结合材料断裂理论分析了切削参数对PTFE切屑毛边演化规律的影响,利用分形理论研究了切削力的波动和切屑毛边数量和出现频率的关系。

1 实验条件和方法

本实验在晶研4060数控雕刻机上进行，采用型号为BAP300R C10-10-100-1T的数控铣刀杆，前角γ0=30°、后角β=11°的陶瓷铣刀片。工件材料为聚四氟乙烯(PTFE)，型号为大金M111，密度为2.17 g/mm3,规格为30 mm×20 mm×20 mm矩形棒料，生产厂家为华尔卡(上海)贸易有限公司。切削力由Kistler三向力传感器、电荷放大器5080A、数据采集系统5697A1测得并采集，采样频率为1 kHz，如图1所示。

图1 实验装置

正交切削采用单因素实验方法，实验参数见表1。将收集到的切屑置于VHX-700F超景深显微镜和扫描电子显微镜(scanning electron microscope，SEM)下观察，并记录其数量和形态。切屑厚度通过电子数显卡尺进行测量，取3次测量的平均值。

表1 实验参数

PTFE材料力学性能见表2。准静态力学实验按照GB/T16421—1996《塑料拉伸性能小试样实验方法》、GB/T 1039—1992《塑料力学性能试验方法总则》在WDW-100微机控制电子万能实验机上进行，拉伸实验所用试样为Ⅱ型试样，拉伸速度为10 mm/min；压缩所用圆柱形材料试样尺寸为φ15 mm×10 mm，名义应变率为1×10-3s-1，压缩速率为0.605 mm/min，进行了两次测试，如图2所示。

表2 PTFE材料力学性能

图2 实验试样与万能实验机

2 实验结果与讨论

2.1 连续切屑形成机理

PTFE连续切屑形成过程如图3所示，实验过程中，PTFE材料切屑一直保持连续状态，此外，SAITO[23]在研究PTFE的切屑变形时发现，刀具前刀面上的工件材料经历了很大的压缩变形，这表明切屑是由刀具前刀面上的压缩变形撕裂而形成的。因此，可利用MERCHANT[24]提出的剪切面理论来分析切屑形成过程，该理论假设工件材料是理想的塑性材料，并在临界剪切应力σs下屈服。如图4所示，切屑经历剪切变形，在刀尖和工件未加工表面之间形成一个角度为φ的剪切平面，当材料去除时，切屑沿着前刀面向上流动，产生的剪切应变γ可表示为

图3 PTFE连续切屑形成过程

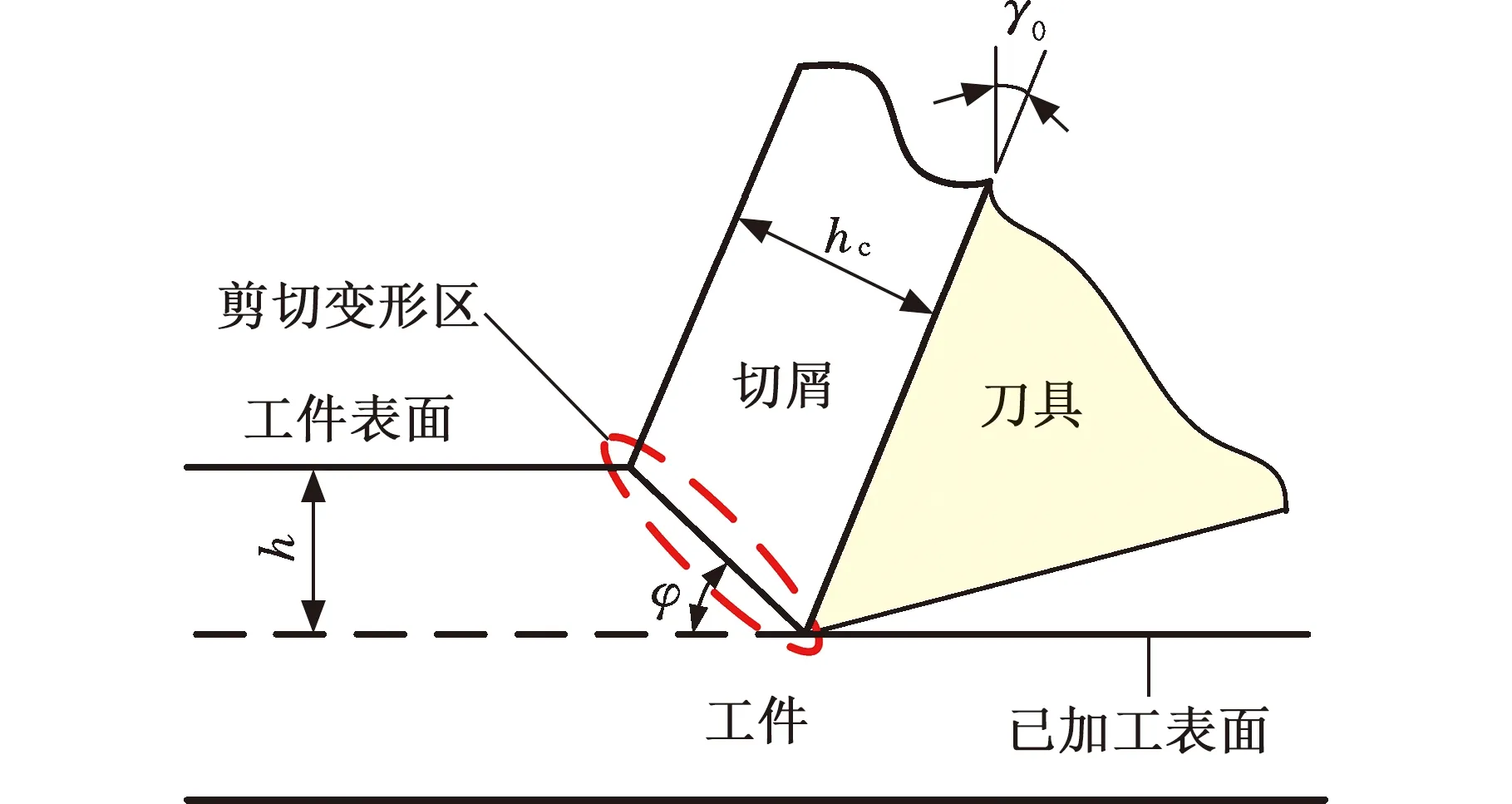
图4 剪切平面模型

(1)

(2)

式中，hc为切屑厚度；h为切削厚度；γ0为刀具前角；φ为剪切角。

(3)

利用上述理论计算每种切深的等效应变，见表3。PTFE是塑性材料，具有很大的屈服应变，图5所示为PTFE材料准静态压缩过程中的真实应力-应变关系，三种不同切削厚度下的真实应力均未超过材料的压缩断裂应力，这表明PTFE正交切削时切屑连续，并未出现断裂现象。

表3 等效应变

图5 PTFE压缩应变-应力关系

2.2 切屑毛边形成机理

针对PTFE材料在正交切削过程中出现的切屑边缘毛边现象(图6)，需要对其形成机理进行探究。如图7a所示，在刀具进给过程中，由于PTFE材料的塑性，切屑中部的材料随着刀尖的移动被前刀面挤压，滑移并堆叠在切屑边缘，出现厚度不均匀、不规则的片层状结构(图7b)，并且出现应力集中区和形状不规则的侧边。

图6 SEM下的切屑毛边

(a)片层状结构

如图8所示，材料所受应力未超过名义屈服点σs，应力释放后发生回弹；而在应变硬化阶段，材料在应力作用下发生了不可逆转的塑性变形；之后应力继续增大，材料到达其拉伸强度σm后发生断裂。在正交切削PTFE材料的过程中，PTFE切屑边缘由于刀具剪切应力的作用，在形成片层状结构之后会发生和单轴拉伸相似的拉伸断裂过程，应力集中区的材料随着刀尖的运动迅速经历弹性变形阶段，在名义屈服点σs处发生屈服，并迅速经历应变硬化阶段，在此过程中，单位面积内材料都发生了不可逆转的拉伸变形，在局部材料的厚度较小位置无法承受刀具的剪切力作用，达到拉伸强度σm后发生断裂。

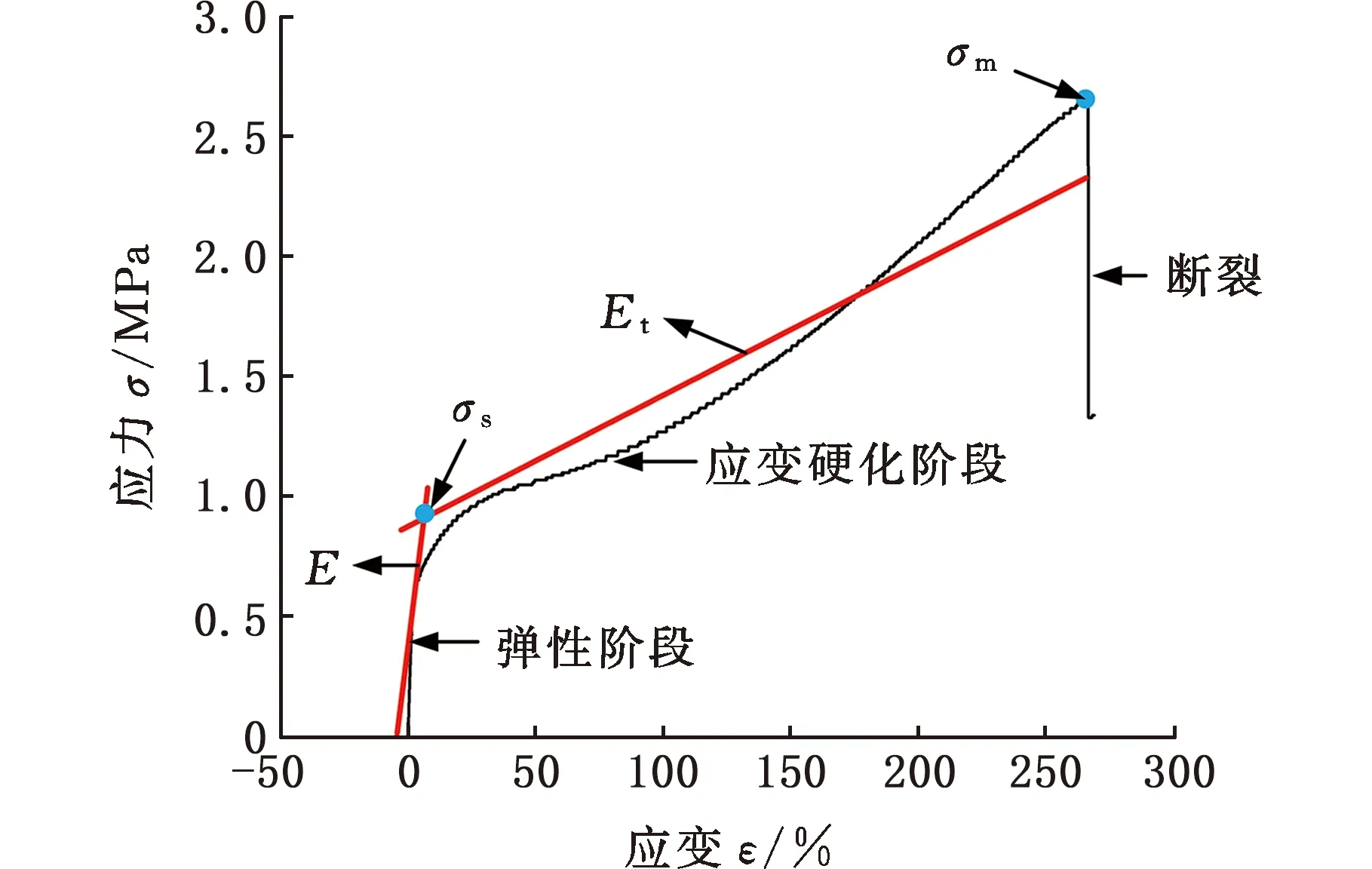
(a)准静态拉伸曲线

图9是切削厚度0.3 mm、切削速度300 mm/min条件下切屑毛边的SEM图像，因为切削速度的增大，切屑毛边的形成过程很不稳定，出现一个并未完全“撕裂”为切屑毛边的椭圆形裂纹，这更有助于探究切屑边缘材料的断裂机理。

图9 裂纹尖端的应力集中情况

图9中，撕开型裂纹的两侧受到一组大小为σ0的相对作用力，而处于裂纹尖端的材料则会出现应力集中现象，受到高应力σm作用，裂纹尖端处的应力可由以下方程表征[25]：

σm=σ0(1+2a/b)

(4)

σm与σ0的比值可用来衡量裂纹尖端应力集中效应的强弱。当a=b时，微裂纹的形状为圆形，裂纹尖端的应力σm是材料所受平均应力σ0的3倍；对于一个形状尖锐的裂纹，可知a≫b，材料裂纹尖端会产生非常大的应力集中效应。毛边形成的瞬间可视为平面应变状态，由Griffith理论可知，材料的断裂强度σb和a-1/2之间存在比例关系，裂纹越长，材料的断裂强度就越低。因此，裂纹前沿足够大区域的应力σ都达到断裂强度的值，导致裂纹在主切削力的作用下沿着材料堆积的侧边失稳扩展和“撕扯”断裂，最终形成大小形状不一的毛边；而毛边多数都是向上卷曲的，这是因为在拉伸断裂之后，由材料的塑性而产生的塑性回弹。

2.3 切削参数对切屑毛边形态的影响规律

在正交切削的过程中，随着切削厚度和进给速度的改变及PTFE材料本身塑性的影响，在第一变形区产生应力集中，影响了裂纹的形核，并改变材料去除过程中裂纹失稳扩展的模式，产生了尺寸和形态不同的毛边。

如图10所示，毛边结构定量评价采用切屑毛边间距Pc和高度Hc两个因素。切屑毛边间距Pc是通过测量6个连续毛边的相邻毛边最高点间距l′并取平均值得出的;切屑毛边高度Hc则是选择5个形态完整的毛边，测量毛边最高点与最低点高度差h′并计算其平均值得出的。即

(a)v=100 mm/min

Pc=(l′1+l′2+l′3+l′4+l′5)/5

(5)

Hc=(h′1+h′2+h′3+h′4+h′5)/5

(6)

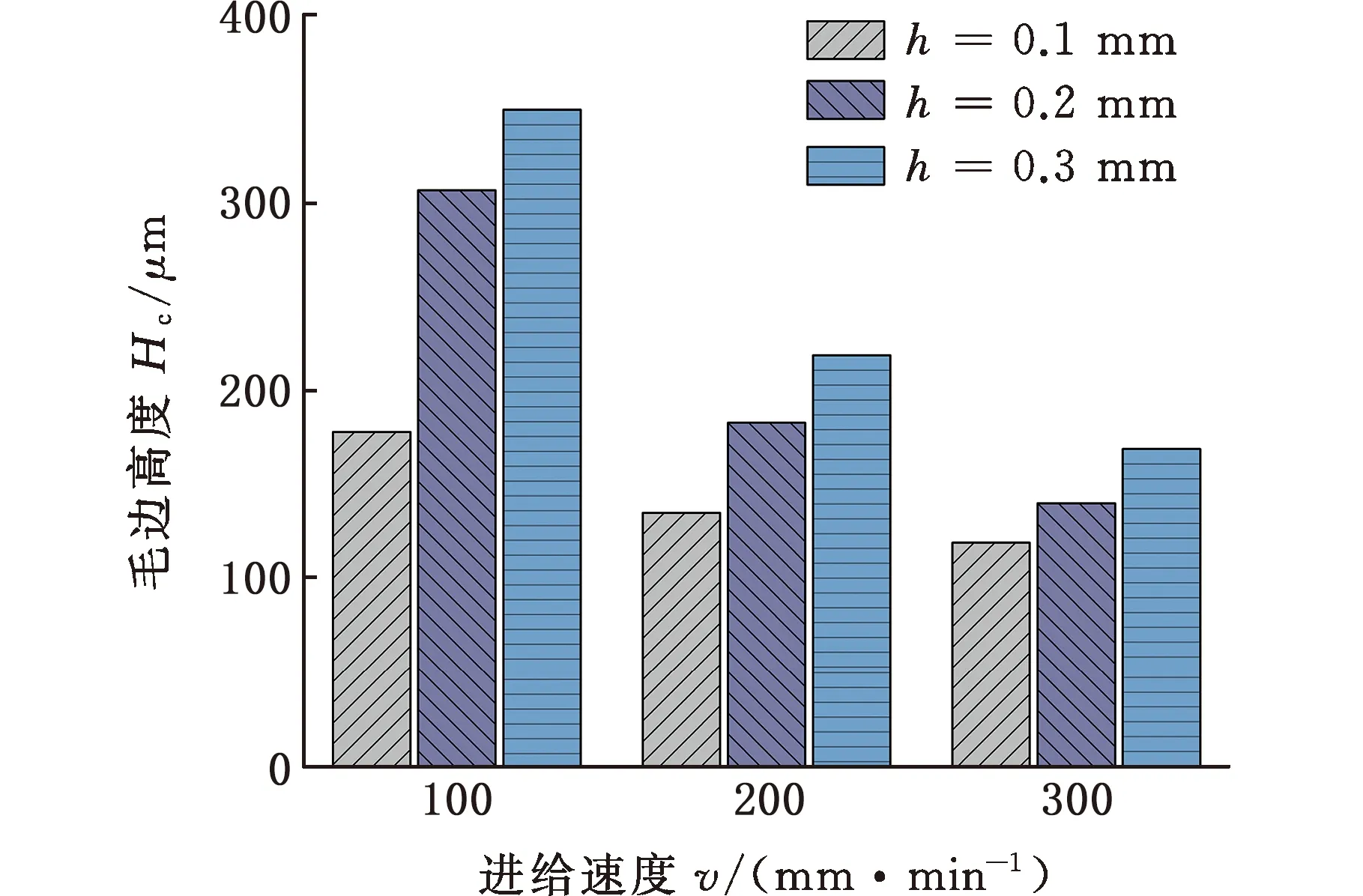
如图11所示，在相同切削厚度的工况下，毛边间距Pc和高度Hc均随着切削速度的增大呈下降趋势，这一现象的产生是由于当切削速度增大时，切屑边缘应力集中速度较快，刀尖处材料的挤压堆叠效应减轻，裂纹迅速在片层状结构的应力集中区形核并扩展断裂，毛边高度减小，毛边形成的周期也因为断裂过程的加快而加快，使得毛边间距变小，切屑边缘更为粗糙。

(a)切削参数对毛边高度的影响

进给速度一定时，毛边高度Hc随着切削厚度的减小而减小。产生这一现象的原因是，小切削厚度有利于切削力的减小，使材料去除更为容易；切屑和前刀面的摩擦力变小，切屑在前刀面上的流动阻力变小，刀尖处的材料塑性挤压堆积减少，减小了第一切削区的应力集中。根据WANG等[13]对聚合物断裂韧性的研究结果，切削厚度减小时，材料的断裂韧性也变小。因此，应力集中区的材料更容易产生裂纹并撕裂为断口，断口在主切削力的作用下沿着材料堆积的侧边扩展。可以看出，切削厚度对毛边间距的影响规律不够明显。

在PTFE材料切屑毛边形成与扩展的过程中，涉及了大量力学变化，具有强烈的非线性特征，引起切削力在其均值上下两端波动，因此可用切削力的稳定性来侧面表征。分形理论对描述复杂的非线性信号和混沌特征有很好的效果[26]，其中，分形维数D是理论中最重要的参数，它反映了图形轮廓的复杂、不规则和精细程度，具有细分轮廓结构的能力，而盒维数法的计算方法简单、高效，故本文通过盒维数法来计算分形维数，对一维切削力信号稳定性进行定量评价。当切削力相对稳定时，切削力波动小，图形细节少，分形维数小[27]。

盒维数法是基于正方形覆盖的思想，将分形曲线用一个边长为r的方盒子覆盖起来，统计不是空盒子的个数，记为N(r)，然后将盒子尺寸进行迭代缩小，当r→0时，分形维数为

(7)

具体计算流程如图12所示。

图12 盒维数计算流程图

毛边的形成过程微观上伴随着各个方向力的变化，因此，分析三向力的合力F有助于全面考虑切削过程中的切削力细节。切削合力F的计算公式为

(8)

式中，Fx为横向力；Fy为切向力；Fz为轴向力。

图13a所示为各个切削区的示意位置，图13b所示为稳定切削区分形维数的求解过程，本文选取每组切削参数下稳定切削区的4699个采样点进行分析，初始方格子边长r需大于数据长度且应取2的幂次，本文取r=213=8192，采用盒维数法拟合直线的斜率即为分形维数D的值，计算每组切削参数下对应的分形维数。

(a)各切削区示意图

如图14所示，将每组切削参数下切削力合力的均值与其对应的分形维数进行对比，结果表明：在同一切削厚度下，随着切削速度的增大，切削合力也大致呈增大趋势；在同一进给速度下，切削合力又随着切削厚度的增大而增大。就分形维数来说，当切削厚度一定时，分形维数随着切削速度的增大而增大，表明切削合力越不稳定，波动越大。产生这一趋势的原因是，切削速度的增大使裂纹快速形核与扩展，单个毛边产生的周期缩短，宏观上毛边的数量增加，切削力的波动变大，分形维数变大。当切削速度一定时，随着切削厚度的增大，分形维数表现出递减的趋势，这是因为在切削厚度增大时，材料的去除越不容易，裂纹越不容易失稳断裂，从而越不容易产生毛边，宏观上表现出毛边数量的减少，使得切削力波动变小，分形维数变小。综上所述，切削速度为300 mm/min、切削厚度为0.1 mm时，分形维数最大，切削力波动最严重，毛边数量最多；切削速度为100 mm/min、切削厚度为0.3 mm时，分形维数最小，切削力最稳定，切屑边缘最平整，这与电镜下观察到的毛边现象是一致的，说明毛边结构随着切削参数的改变而改变，对切削力的稳定性产生了影响。

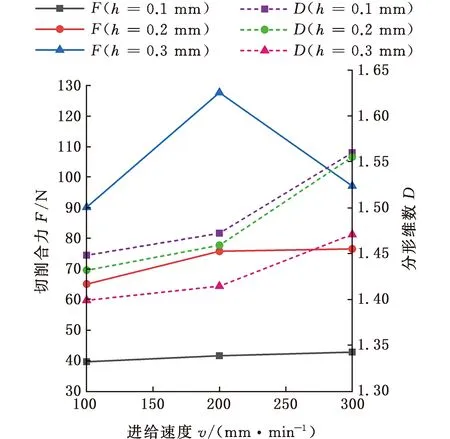
图14 切削参数对切削合力和分形维数的影响

3 结论

(1)基于剪切面理论对三种不同切削厚度对应切屑的等效应变进行计算，发现其对应的真实应力均未超过材料的压缩断裂应力，故PTFE材料切屑为连续状态。

(2)基于断裂理论对PTFE材料切屑边缘的SEM图像进行分析，由于刀具前刀面对PTFE材料的挤压堆叠，使得材料向切屑边缘流动，继而在切屑边缘形成片层状结构，而片层状结构前端的应力集中区聚集了大量应力，超过了其拉伸强度并断裂，首先出现裂纹，随后裂纹在主切削力作用下沿着材料堆积的侧边进行扩展，最终形成了切屑毛边。

(3)利用毛边结构定量评价分析了切削参数对PTFE材料切屑毛边形态的影响规律，结果发现：当切削速度增大时，切屑毛边高度和间距均呈减小趋势；当切削厚度增大时，切屑毛边高度增大，而对切屑毛边间距的影响不明显。

(4)运用分形理论对正交切削PTFE材料的切削力稳定性进行了评估，发现切削力的波动宏观上反映出毛边形成的数量和出现的频率；之后对比了不同切削参数下切削力的稳定性，发现当切削厚度为0.3 mm、切削速度为100 mm/min时，切削力波动最小，PTFE材料切屑边缘最平整。