数学竞赛、强基计划中不定方程解法探究
徐小花 李丽荣 杨 平 (北京市日坛中学 100020)
1 因式分解法
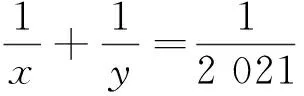
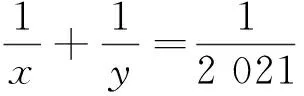
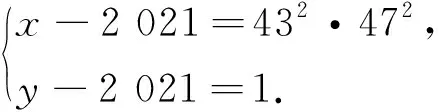
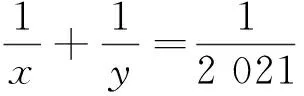
例2(2021清华大学领军计划第1题)已知a,b,c,d都是正整数,且a3=b2,c5=d4,c-a=77,求d-b.
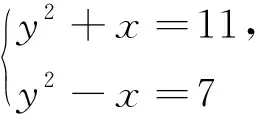
例3(2021北京大学优秀中学生寒假学堂第4题)若m3+n3+99mn=333,且m,n∈N*,则(m,n)有组.
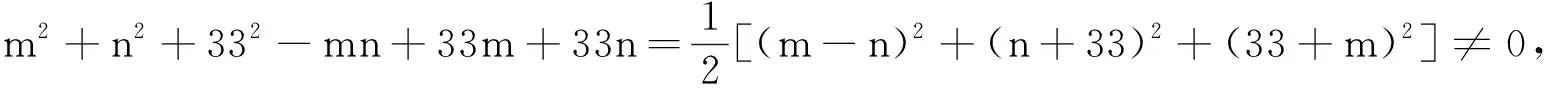
点评通过例2和例3可以看出,运用因式分解法求解不定方程的最大困难点就是对所给条件进行因式分解,而且是通过利用整数分解的有限性和唯一性来解决的,不是彻底分解,也就是常常将因式分解法与整除结合起来.下面给出的几道小题供读者练习因式分解法.
练习1 (2020北京大学强基计划第7题)方程19x+93y=4xy的整数解的个数为( ).
A.4 B.8 C.16 D.前三个答案都不对
提示 19x+93y=4xy⟹(4x-93)(4y-19)=19×93=3×19×31.(参考答案:B)
练习2 (2020中国科技大学创新班初试第5题)x2-y2=4p2,x,y为正整数,p为素数,则x3-y3=.
提示x2-y2=4p2⟹(x-y)(x+y)=4p2=22·p2.(参考答案:6p4+2)
练习3 (2020上海交通大学强基计划第14题)方程x(x+1)-1=y2的正整数解的个数为.
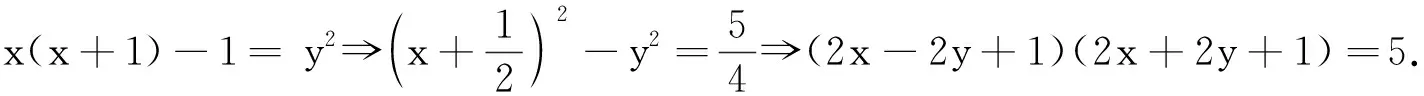
2 取模同余法
例4(2020复旦大学自主招生第21题)方程3x+4y+12z=2 020的非负整数解的组数为.
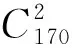
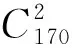
例5(2021北京大学语言类保送试题第11题)设a,b是正整数n的正因素,使得(a-1)(b+2)=n-2,则n可以等于( ).
A.2 0202 020B.2×2 0202 020
C.3×2 0202 020D.前三个答案都不对
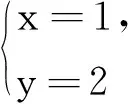
点评充分利用条件“a,b是正整数n的正因素”,等价转换为n≡0(moda),n≡0(modb),再利用同余定理可以进一步获得a与b之间的数量关系,在问题的解决过程中也用到了因式分解法.同样我们给出两道小题供读者练习取模同余法.
练习4 (2016清华大学领军计划第13题)关于x,y的不定方程x2+615=2y的正整数解的组数为.
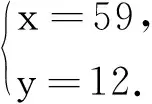
练习5 (2020北京大学优秀中学生暑假体验营第1题)已知正整数a,b,n满足a!+b!=5n,求(a,b,n).
提示 由奇偶性原则可以判断出a=1,b为偶或b=1,a为偶.不妨设a=1,再由5n≡0(mod 5),可知当b≥5时,a!+b!≡1(mod 5)不符合题意,对b=1,2,3,4逐一检验.(参考答案:(1,4,2)或(4,1,2))
3 分类讨论法
例6(2021全国高中数学联赛福建预赛试题第10题)若整数a,b,c满足0≤a≤10,0≤b≤10,0≤c≤10,10≤a+b+c≤20,则满足条件的有序数组(a,b,c)共有组.
方法1 设a+b=t,则0≤t≤20.
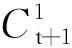
当11≤t≤20时,满足条件的(a,b)有(21-t)对,此时0≤c≤20-t,c的取值有[(20-t)-0]+1种,即(21-t)种.此时满足条件的有序数组(a,b,c)共有(21-t)2组.
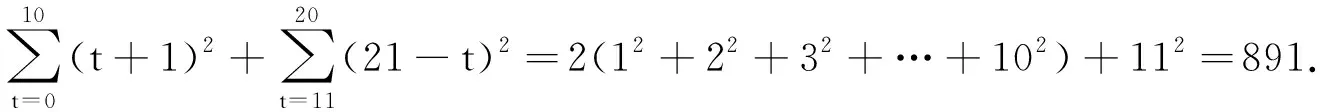
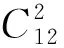

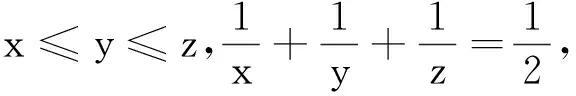
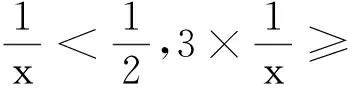
本文仅列举了求不定方程整数解的三种常用策略,其实在求解不定方程问题时常常还会用到格点法、枚举法、奇偶分析法等更加基本的方法.很多问题往往需要先用本文介绍的因式分解法、取模同余法和分类讨论法这三种方法转化构造后再借助基本方法得到最后结果.

