基于稳健方差分析的多重与多元线性回归模型比较——以美国共享单车公司CapitalBikeshare为例

刘佳仑

（首都经济贸易大学 北京 100026）

一、数据集介绍及数据预处理

本文以美国华盛顿特区的共享单车公司CapitalBikeshare，在2011—2012年间所记载的数据为目标数据集，选取当天是否为工作日、所处季节、天气状况、气温、体感温度、湿度、风速这七个关键指标作为解释变量，探索其与每日临时用户数量、注册用户数量、用户总量之间的关系。对所选变量的具体说明如表1所示。

表1 所选变量及相关信息

接下来做数据预处理。首先，将数据集中tmp、atmp、hum、windspeed的标准值还原为实际值；其次，删除2011年3月10日的异常数据，因为这一天的hum值显示为0，实际生活中不可能出现这样的情况；最后，为避免建模时出现多重共线性的情况，对含有两个以上值的定性变量season和weathersit分别进行独热编码处理，对应转化为3个和2个哑变量。其中，将weathersit转化为2个哑变量，是因为它的实际取值中并没有出现过（大雨、大雪、大雾））极端天气。

二、多元与一元方差分析

（一）多元单因素方差分析

做多元单因素方差分析时有两个假设前提，分别为待检验总体的多元正态性和方差—协方差阵的同质性。前者可用Q-Q图来进行检验，对于后者本文采用似然比检验。

1.多元正态性检验

多元向量的Q-Q图通过展示卡方分布理论值与样本值的关系，来判别待检验总体是否满足正态性假设。如果所有点都落在斜率为1、截距为0的直线附近，则认为正态性假设成立。应用R软件，得到响应向量（casual,registered）针对三个因素workingday、season、weathersit的Q-Q图如下。

图1（casual,registered）的Q-Q图

结果显示，响应向量（casual,registered）在不同因素下均服从多元正态分布。

2.协方差阵同质性检验

本小节中，响应向量（casual,registered）将针对三个因素workingday、season、weathersit分别做三次似然比检验，以验证待检验总体协方差矩阵的同质性假设。

这里以workingday为例来说明检验流程。首先，应用R软件的str函数来查看workingday在不同水平下响应向量的数据条数，所得结果记为n0=231，n1=499。将组别0和组别1中响应向量的数据矩阵分别记为Z0和Z1，在正态性假设下有Zi～Nni*q( )μi,Ini⊗Σi(i=0,1)。然后构造幂等矩阵，令其中1ni为全1列向量，于是有根 据 幂 等 矩 阵 性 质 可 得，Ui=其分布为且在U0和U1之间相互独立。

所检验的问题为：H0:Σ0=Σ1v.s.HA:Σ0≠Σ1；似然比检验统计量为：

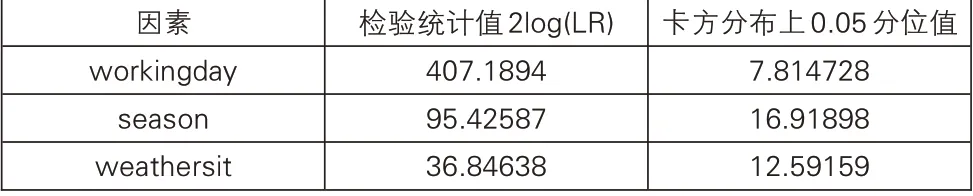
表2 似然比检验结果

各检验统计值均大于相应原假设下卡方分布上的0.05分位数。因此，在0.05的显著性水平下拒绝原假设，认为针对上述三个因素进行多元方差分析时，协方差矩阵同质性的检验均未能通过，即协方差矩阵不齐，于是后续采用稳健多元方差分析的方法继续进行检验。

3.稳健多元单因素方差分析

若多元正态性或者协方差矩阵同质性假设不满足，又担心多元离群点，那么需考虑采用稳健的MANOVA检验，此方法可通过R语言rrcov包中的Wilks.test函数来实现。检验结果如表3。

表3稳健单因素MANOVA

根据表3，所检验的三个因素对应的p值均小于0.05，于是在0.05的显著性水平下拒绝原假设，认为共享单车每日临时用户数量与注册用户数量所构成的响应向量，在工作日与非工作日之间、在不同季节之间、在不同天气状况下的均值，都存在显著性差异。

（二）一元单因素方差分析

以共享单车每日用户总数cnt作为响应变量，以workingday、season、weathersit作为影响因素，分别做一元单因素方差分析。由于此方法的相关研究已经非常普遍，故本文不再详细阐述其检验步骤。检验正态性仍使用Q-Q图；判断方差齐性选用Bartlett检验。值得注意的是，当检验因素各水平总体难以满足方差分析假设条件（独立性、正态性、方差齐性）时，可采用克罗斯考尔和瓦里斯在1952年提出的Kruskal-Wallis稳健检验方法。

对假设前提进行检验，cnt在各因素下基本满足正态性假设，并且除season外在其他因素下满足方差齐性假设，故对season使用Kruskal-Wallis稳健检验。方差分析检验结果表明，在0.05的显著性水平下，cnt在工作日与非工作日的均值不存在显著性差异，在不同天气状况下的均值存在显著性差异，在不同季节的均值存在显著性差异。

三、多元与多重线性回归模型的建立

构建多元线性回归模型，以casual和registered作为响应向量，以workingday、season_1、season_2、season_3、weathersit_1、weathersit_2、temp、atemp、hum、windspeed作为解释变量；构建多重线性回归模型，以cnt作为响应变量，其解释变量与多元线性回归模型的设置相同。然后将分别对上述两个模型进行估计、检验及修正，以达到最优。

（一）多元线性回归模型

1.参数估计

设Y=(Y1,Y2)为casual和registered构成的响应向量，x=(1,x1,x2,…x10)为解释变量，R为随机误差项。于是可构建多元线性回归模型：

在上述模型中，β的估计量为的估计量为其 中n＝730为 总 样本量，p＝11为x的列数，l＝2为β的列数。根据以上表达式应用R软件，即可输出β和ΣR的估计值。

2.β中行参数的Hotelling’sT2检验

（1）提 出 原 假 设 与 备 择 假 设：H0∶βi=0v.s.H1∶βi≠0

（2）应用R软件，计算βi的F检验统计值。

表4 行参数的F检验统计值

3.模型修正

在原多元线性回归模型的基础上，剔除掉自变量atemp后，再做一次回归，得到新模型中未知参数β′的估计值如表5。

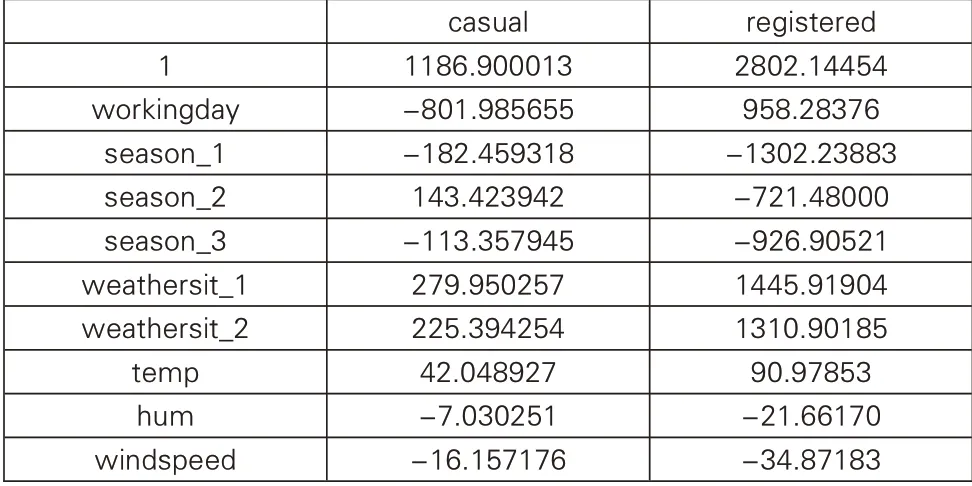
表5 β′的估计值

对β′的行参数做Hotelling’sT2检验，得到行参数的F检验统计值如表6。

表6 行参数的F检验统计值

（二）多重线性回归模型

1.参数估计及t检验

设Y3为共享单车每日用户总数cnt，x同多元线性回归模型，R为随机误差项，构建多重线性回归模型：

应用R软件的lm函数，得到β*的估计值及其各元素相应的t检验p值如表7。

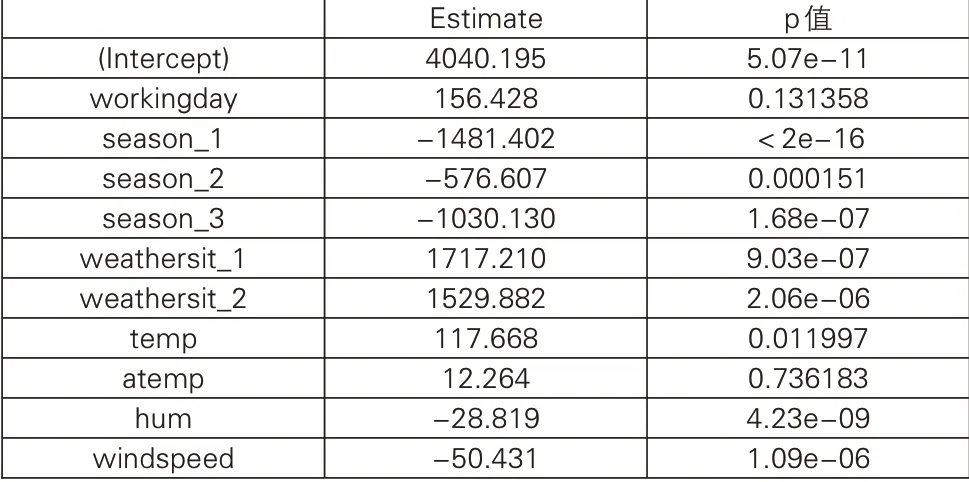
表7 β＊的估计值及t检验结果

当p＜0.05时，在0.05的显著性水平下拒绝原假设，即认为相应的当p＞0.05时，在0.05的显著性水平下不拒绝原假设，即认为相应的通过观察表7可知，解释变量workingday和atemp的参数均未能通过检验，于是需对此模型进行修正以达最优。

2.逐步回归法修正模型

R语言做逐步回归分析时，以赤池信息量AIC值的最小值作为确定最优模型的准则。采用逐步回归分析方法对上述多重线性回归模型进行修正，依次剔除解释变量atemp和workingday，修正后的模型为：

cnt＝4125－1482season_1－581season_2－1049season_3＋1700weathersit_1＋1524weathersit_2＋134temp－29hum－51windspeed

R语言运行结果显示：在修正模型中，每一个解释变量对于响应变量cnt的线性影响都是显著的。

四、结论

多元线性回归和多重线性回归对于没有统计学背景的研究人员而言，确实是两个非常容易被混淆的概念，通常会认为二者是等价的，但通过上文叙述，可以很明确地看出二者之间的区别与联系。多重线性回归（multiplelinearregression）是简单直线回归的推广，研究的是一个因变量与多个自变量之间的数量依存关系。而多元线性回归（multivariate linearregression）则是多重线性回归的推广，研究的是具有相关关系的多个因变量组成的响应向量，与多个自变量之间的数量依存关系。虽说从形式上来看，多元线性回归模型是多重线性回归模型的简单叠加，但实际上，它的用途和研究意义都比后者更加广泛。一方面它能够衡量响应向量在不同维度之间的相关关系，另一方面它可以探究某一解释变量对研究总体在不同维度的综合影响。接下来，对两类模型的构造方式和建模流程进行详细的分析和对比。

在多元单因素方差分析部分，响应向量（casual,registered）针对三个因素workingday、season、weathersit均通过了显著性检验，说明这三个因素对响应向量都具有显著影响。于是在构建多元线性回归模型时，应纳入上述三个因素作为解释变量，从表5呈现的信息来看事实也正是如此。一元单因素方差分析检验结果显示，响应变量cnt在workingday各水平下的均值并无显著性差异，但对因素season和weathersit都通过了显著性检验，这与构造多重线性回归模型时，不纳入workingday但纳入其余两个因素作为解释变量的事实相符。

综上，无论多元还是一元方差分析结果，都与各自所构造的回归模型相互验证了彼此的正确性。另外，被解释变量的维数设置体现了两类回归模型在构造方式上最明显的差别，多元模型设置多维响应向量，多重模型仅设置一维响应变量。

在多元线性回归部分，从表5可以看出，解释变量workingday对临时用户数量具有负的线性影响，而对注册用户数量有正的线性影响，意味着工作日相比于非工作日，临时用户数量将减少，而注册用户数量增多。解释变量season经分解后形成了代表春、夏、秋季的哑变量，对比冬季，春、夏、秋季的注册用户数量均呈现出负增长，春季和秋季的临时用户数量也呈现出负增长，但夏季的临时用户数量呈现出正增长，这表明夏季的临时用户数量比冬季更多。解释变量weathersit经分解后形成了代表好天气和较好天气的哑变量，对比较差天气，好天气和较好天气下的临时用户数量和注册用户数量均呈现出正增长趋势。此外，在所设定的气温范围内，温度越高，临时用户数量和注册用户数量越多；在所设定的湿度和风速范围内，湿度和风速水平越高，临时用户数量和注册用户数量越少。上述分析结果基本符合实际情况。

在多重线性回归分析中，对比冬季，春、夏、秋这三个季节对每日用户总数均呈现出负的线性影响，意味着春、夏、秋三个季节的每日用户总数少于冬季。对比较差天气，好天气和较好天气对每日用户总数具有正的线性影响，意味着天气越好每日用户总数越多。此外，在定量解释变量的研究范围内，温度越高，每日用户总数越多；湿度、风速越高，每日用户总数越少。以上内容基本与多元线性回归的分析结果保持一致，但获得的信息明显少于多元模型。