耦合MaxEnt模型的望谟县滑坡易发性对比研究
张泽方
(贵州民族大学 建筑工程学院,贵州 贵阳 550025)
滑坡易发性评价指根据已经发生的滑坡灾害的特征,对可能发生滑坡灾害的倾向性进行评价,确定成灾概率的大小。早在20世纪70年代,国外学者就已经开展滑坡易发性研究工作,Brabb等[1]主要考虑地质因素,制作了美国加州San Mateo地区的派生地图,更加简洁地表达了滑坡易发区信息。我国滑坡易发性研究起步较晚,1991年,狄君靖[2]对云南省地质灾害控制因素进行了分析研究,并在此基础上作了滑坡易发性分区,为后续研究提供了数学模型参考。目前,国内外滑坡易发性评价模型主要包括概率统计模型、机器学习模型等,其中概率统计模型包括信息量模型[3]、确定性系数模型[4]、证据权模型[5]、二元逻辑回归模型[6]等,机器学习模型包括神经网络模型[7]、随机森林模型[8]、决策树预测模型[9]、支持向量机模型[10]等。然而,对于单一模型,在环境因子的状态分级与量化处理中存在主观因素干扰的问题以及无法客观确定不同环境因子权重的缺陷。因此,两种甚至多种模型耦合的评价方法逐渐成为近年来探索的热点。郭子正等[11]将WOE模型和BP神经网络模型结合用于三峡万州区滑坡易发性评价,研究表明WOE-BP模型较两种单一模型更为精确;张玘恺等[12]以九寨沟县为研究区,基于I、CF和LR模型,提出LR-I和LRCF耦合模型,显著提高了评价精度;仪政等[13]通过信息量与多模型耦合的方法对三峡库区秭归县侏罗系地层区进行滑坡易发性评价,结果表明耦合模型比单一信息量模型具有更高的预测精度;刘璐瑶等[14]将证据权与逻辑回归模型结合用于浙江省永嘉县滑坡易发性评价,此评价结果的合理性与精确度均优于两种单一模型。上述分析表明,滑坡易发性评价的模型丰富多样,对不同区域而言不一定存在相同的最优模型[15],耦合模型的精度总体上高于单一模型。因此,本文尝试将最大熵模型(MaxEnt)与信息量模型(I)、确定性系数模型(CF)进行耦合,通过各模型对比研究,探讨适用于望谟县的滑坡易发性评价模型。
1 模型方法
1.1 最大熵模型(MaxEnt)
最大熵(MaxEnt)模型是由Phillips等[16]基于机器学习和数理统计方法开发的预测物种地理分布的生态位模型,当前已经有学者在滑坡易发性评价中引入MaxEnt模型[17]。MaxEnt模型的特征函数f(a,b)可表示a,b的某种定性关系,当a,b符合特定条件时,特征函数赋值为1;不符合特定条件时,特征函数赋值为0[18]。给定一个约束条件,将训练数据视为随机变量(a,b)产生,令p(f)表示特征函数f(a,b)关于经验分布p(a,b)的期望,如下式:
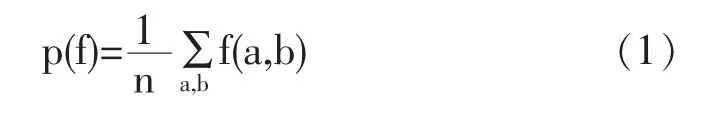
若符合约束条件,则p(b|a)关于函数f的期望,与经验分布关于f(a,b)的期望相等:
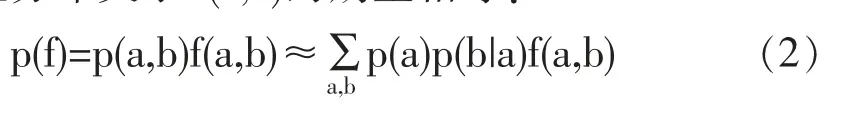
再求解带有约束条件的最优化问题,根据归一化指数exp(1-ω)[17],令Zω(a)表示exp(1-ω),得:
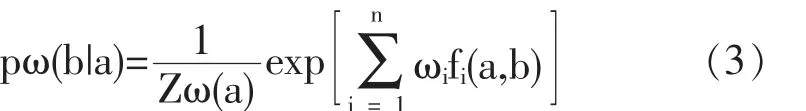
1.2 信息量模型(I)
信息量模型是一种基于信息论的统计模型,它能将代表环境因素的数值转化为反映滑坡易发性的信息量值,信息量值越大表示发生滑坡的可能性越大,信息量值越小表示发生滑坡的可能性越小,其计算公式如下:
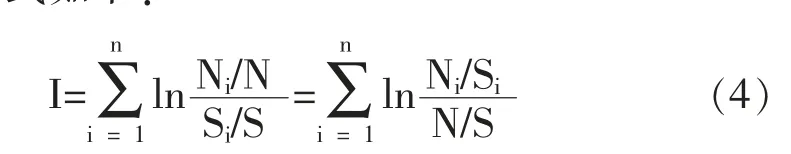
I为单个栅格内的总信息量值,n为环境因子个数,Ni为研究区某特定环境因子内滑坡灾害分布面积;N为研究区内滑坡灾害分布总面积;Si为研究区内某特定环境因子的面积;S为研究区总面积;N/S为研究区的滑坡灾害分布密度,Ni/Si为滑坡灾害在某图层特定级别内的分布密度。
1.3 确定性系数模型(CF)
确定性系数模型是由Shortiffe等[19]提出的一种概率函数模型,目前已广泛应用于滑坡灾害易发性评价研究,CF值越大表示该环境下越易发生滑坡,反之则表示越不易发生滑坡,其计算公式如下:
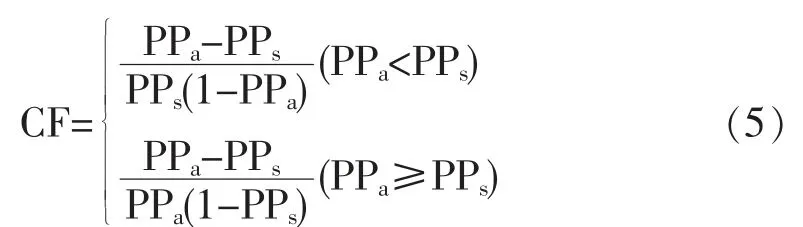
式中CF为滑坡灾害发生的确定性系数;PPa为滑坡灾害在环境因子分类a中发生的条件概率,可用环境因子分类a中的滑坡灾害面积与分类面积的比值表示;PPs表示滑坡灾害在整个研究区中发生的先验概率,可用滑坡灾害总面积与研究区总面积的比值表示,在研究区确定的情况下,PPs通常是一个定值。
1.4 多模型耦合
信息量模型和确定性系数模型可以获取到各环境因子的信息量值和确定性系数值,这些值虽然从不同角度反映了各环境因子对滑坡的影响程度,但是并未确定各环境因子的权重,而最大熵模型可以根据模型中各环境因子的贡献率确定其权重,因此本文将最大熵模型和信息量模型、确定性系数模型耦合,从而对研究区进行更加准确的滑坡易发性评价。
2 研究区概况及评价流程
2.1 研究区概况
研究区为望谟全县,地理位置介于东经105°49′~106°32′、北纬24°53′~25°38′之间,总面积约为3018km2,如图1所示,研究区地形地貌、地质构造与滑坡灾害点分布情况。望谟县地处云贵高原向广西丘陵过渡的斜坡地带,平均海拔高度为868米,地势北高南低,地貌形态以山地、丘陵为主,盆地较少。研究区内属亚热带季风湿润气候,年均气温19.5℃,年均降雨量为1421.1mm;褶皱断裂发育,新构造活动强烈,岩土体组合复杂多样,东西部岩溶发育较为典型;地表水系发育,其中河流长度大于10km或流域面积大于20km2的河流共27条,属山区雨源性河流,侵蚀作用较强烈。区内突发性地质灾害类型有滑坡、崩塌、泥石流、地面塌陷等,其中滑坡最为突出,且造成的危害最大。

图1 研究区地理位置及概况
2.2 数据来源及技术路线
研究数据包括滑坡数据和各环境因子数据,其中滑坡数据、年平均降雨量数据来源于中国科学院资源环境科学与数据中心(https://www.resdc.cn);DEM数据和卫星影像数据取自地理空间数据云(https://www.gscloud.cn),在DEM基础上提取了高程、坡度和坡向,NDVI是通过ENVI5.3软件对卫星影像处理得到;地质数据取自国家地质资料数据中心(https://www.ngac.org.cn)1:250万中国地质图,包括岩性和断层分布数据,将岩性按照坚硬程度划分为坚硬岩、较坚硬岩、较坚硬岩夹软岩和软岩,另外计算断层的欧氏距离得到距断层距离数据;土地利用数据来源于GlobeLand30数据集(http://www.globallandcover.com);水系和道路分布数据取自全国地理信息资源目录服务系统(https://www.webmap.cn),通过计算道路和水系的欧氏距离得到距道路距离和距水系道路数据。
望谟县滑坡易发性评价技术路线如图2所示。通过ArcGIS软件的裁剪、投影和重采样等功能模块,将各环境因子的投影坐标统一为WGS_1984_UTM_48N,栅格大小设置为30m×30m;从滑坡数据库中随机选取2/3的样本点作为训练样本,和环境因子共同参与各模型的训练,剩余1/3的样本点作为验证样本对各模型的精度进行检验。
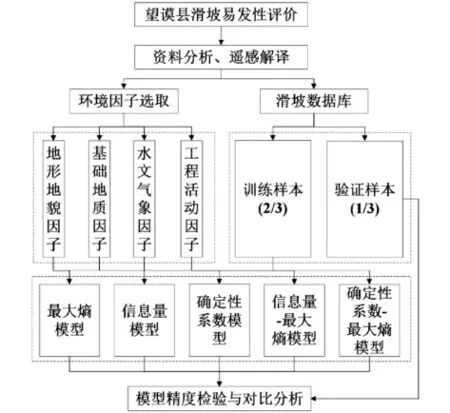
图2 技术路线
3 环境因子分析
3.1 环境因子选取
滑坡灾害的发生受多种环境因素共同作用的影响,本文综合地形地貌、基础地质、水文气象、工程活动等因素,选取高程、坡度、坡向、NDVI、地层岩性、距断层距离、距水系距离、年平均降雨量、土地利用和距道路距离共10个环境因子作为评价指标,如图3所示。

图3 环境因子
对于离散型的环境因子,采用固有的自然分组进行分级,对于连续型的环境因子,采用等步长进行分级。在ArcGIS中使用多值提取至点工具将环境因子数值提取到滑坡训练样本上,再通过公式(4)和公式(5)求出各分级状态下的信息量值和确定性系数值,如表1所示。

表1 各环境因子分级和结果值
3.2 环境因子独立性检验
为了保证各环境因子间的相互独立性和评价结果的可靠性,运用GIS主成分分析功能,进行因子独立性检验,各因子之间的相关系数矩阵见表2(X1~X10分别表示土地利用、高程、地层岩性、坡度、坡向、距断层距离、距水系距离、距道路距离、NDVI、年平均降雨量)。根据金勇进[20]对相关性大小的划分标准,当R小于0.3时,认为各因子之间不相关。如表2所示,各环境因子相关性均符合独立性检验。
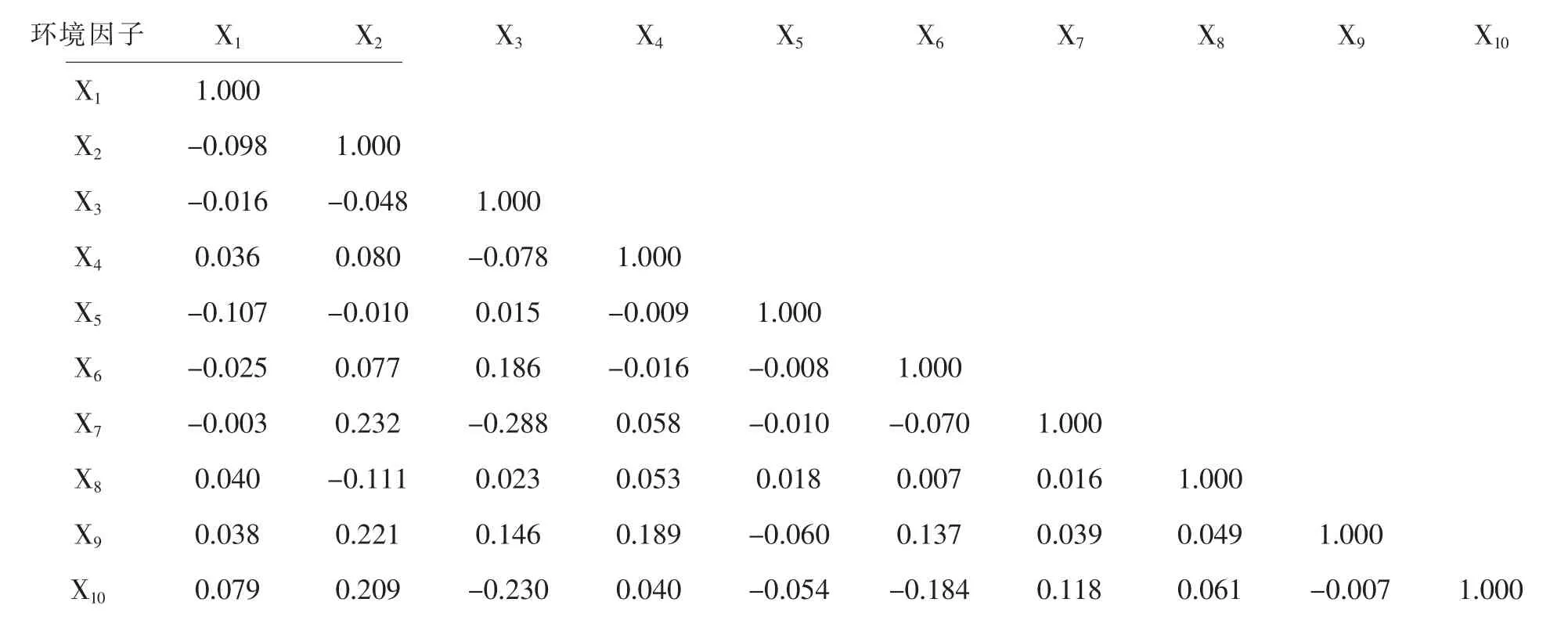
表2 环境因子间的相关系数矩阵
4 评价结果及检验
4.1 滑坡易发性区划
在GIS平台分别将各环境因子的信息量值、CF值进行叠加,得到滑坡信息量值分布图、滑坡CF值分布图;将各环境因子图层和滑坡训练样本导入到MaxEnt软件中,得到基于MaxEnt模型的滑坡易发性概率分布图;分别将各环境因子的信息量值、CF值和滑坡训练样本导入到MaxEnt软件中,得到基于I-MaxEnt模型、CF-MaxEnt模型的滑坡易发性概率分布图;然后将上述分布图根据自然断点法划分为5个易发区:高易发区、中高易发区、中易发区、中低易发区、低易发区,最终得到各模型滑坡易发性区划,如图4所示。
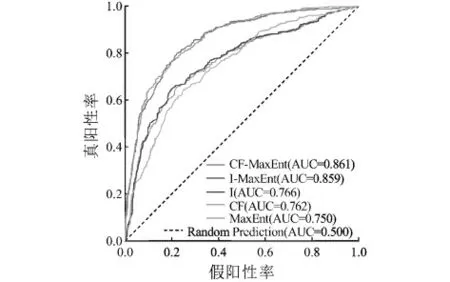
图4 各模型ROC曲线
4.2 频率比检验
频率比即滑坡比与分级比的比值,用以辅助判断分类级别内滑坡易发性程度。频率比越大,易发性程度越高,反之则越低。将易发性区划图和滑坡验证样本进行叠加分析,具体结果如表3所示。I模型在高易发区、中高易发区中分级比共占15.86%,滑坡比共占52.39%,CF模型在高易发区、中高易发区中分级比共占16.05%,滑坡比共占51.39%,MaxEnt模型在高易发区、中高易发区中分级比共占22.93%,滑坡比共占46.84%,I-MaxEnt模型在高易发区、中高易发区中分级比共占19.43%,滑坡比共占73.59%,CF-MaxEnt模型在高易发区、中高易发区中分级比共占18.66%,滑坡比共占73.26%。5种模型的频率比值从低易发区到高易发区均在增大,说明各模型的评价结果与实际相符;其中耦合模型在高易发区的频率比显著大于单一模型对应的频率比,即耦合模型在高易发区中包含了更多的滑坡信息,因而能更加有效地评价望谟县的滑坡易发性。

表3 各模型不同易发区比值
4.3 ROC曲线检验
目前认可度较高的模型评价指标为受试者工作特征(ROC)曲线,其纵轴为真阳性率(灵敏度),即实际上是滑坡灾害且模型判断为滑坡灾害的概率;其横轴为假阳性率(特异度),即实际上非滑坡灾害且模型判断为非滑坡灾害的概率。ROC曲线下面积为AUC值,AUC值介于0~1范围,其越接近1,模型预测效果越好,在0.5~0.6、0.6~0.7、0.7~0.8、0.8~0.9、0.9~1.0时分别表示预测效果失败、较差、一般、好、特别好。由图5可知,MaxEnt、I、CF、IMaxEnt和CF-MaxEnt的AUC评价精度分别为0.750、0.766、0.762、0.859和0.861,其中I-MaxEnt和CF-MaxEnt耦合模型精度优于单一的I、CF、MaxEnt模型精度,且预测效果达到“好”的水平,这表明MaxEnt与多模型耦合的方法适用于望谟县的滑坡易发性评价研究。
5 结论
本文以望谟县为研究区,选取了高程、坡度、坡向、NDVI、地层岩性、距断层距离、距水系距离、年平均降雨量、土地利用和距道路距离共10个环境因子,分别采用信息量模型(I)、确定性系数模型(CF)、最大熵模型(MaxEnt)以及耦合模型建立相应的滑坡易发性区划。
通过受试者工作特征(ROC)曲线检验各模型精度,MaxEnt、I、CF、I-MaxEnt和CF-MaxEnt的AUC评 价 精 度 分 别 为0.750、0.766、0.762、0.859和0.861,耦合模型的预测精度明显优于单一模型,其中确定性系数-最大熵耦合模型(CF-MaxEnt)预测效果相对较好。
本文考虑的环境因子未必全部表达望谟县的环境特征,添加更多环境因子参与模型构建可能会提高评价的精度,另外,本文提出的易发性评价模型也许并非最佳,需要再增加其他评价模型进行对比分析,这些将在后续研究中做进一步探讨。

