基于GWO-LightGBM的冲击地压预测模型
郑 豫
(安徽理工大学 经济与管理学院,安徽 淮南 232000)
在煤矿的开采工作当中,冲击地压是一种十分常见的地质灾害,冲击地压指由于积压在巷道或工作面周围的岩体的弹性变形能的瞬间释放而产生剧烈破坏的现象[1],其往往伴随着岩石体的抛出,工作巷道的破坏和闭合。
世界上许多国家都发生过冲击地压灾害,在1738年英国南史培福煤田发生了第一例有记录的冲击地压灾害,我国有记录的最早冲击地压现象于1933年发生在抚顺胜利煤矿[2]。数十年来,由于我国经济发展的需要,对煤矿的开采深度和强度在不断地增加,这也导致冲击地压逐渐成了我国煤矿开采工作中的巨大危害。2001年1月6日和12日抚顺老虎台矿的两次2.8级冲击地压造成4人死 亡36人负伤[3],2011年11月3日,河南省义马千秋煤矿发生一起重大冲击地压事故,巷道发生严重的挤压垮冒,造成10人死亡[4],2021年10月11日,陕西胡家河煤矿发生较大冲击事故,造成4人死亡[5]。
冲击地压灾害的频繁发生引发人们对冲击地压预测技术的高度关注,传统的冲击地压预测常采用经验类比法和综合指数法,即在综合分析冲击地压指标得基础上,判断是否有冲击地压发生的危险。而大多数综合评价法和经验类比法都需要确定各项指标的权重和对应的分类标准。由于指标的权重和分类标准具有高度的主观性,因此传统预测方法并没有很好的预测效果。而利用机器学习来预测冲击地压则能有效地避免类似的不一致性问题,因此,越来越多的人使用机器学习去预测冲击地压,例如支持向量机(SVM)、BP算法、随机森林(RF)、神经网络等。陈刚等人通过基于神经网络与退火算法来预测冲击地压,这是国内较早的基于机器学习的冲击地压预测模型[6];管少君等人将决策树应用于冲击地压预测中,结果也比较理想[7]。Liang将RF、GBDT、Adaboost、XGBoost和LightGBM分别对冲击地压的微震数据进行分析,预测其危险性,得出RF预测准确度最高[8]。上述方法在预测过程中虽然表现出了一定的准确率,但是处理速度慢需要较长的调参时间和训练时间,并且由于传统的网格调参方法在面对多维度变量时,运行速度特别慢,而且不能将已经搜索过的参数有效转化为先验信息,并与后续的最优参数选择(即后验)建立联系。因此最终得出的模型可能不是最佳预测模型。因此,本文通过灰狼算法预先对LightBGM算法的超参数进行快速择优,其将已搜索过的参数作为参数的先验信息并以其为基础选择出最优(后验)参数。建立GWO-LightBGM预测模型,该模型不仅可以解决这些问题,而且操作简单,预测准确率较于传统的XGboost和支持向量机(SVM)也有明显的优势。
1 GWO优化LightBGM的基本理论
1.1 灰狼优化算法
灰狼优化算法是一种基于灰狼群捕食过程的群智能优化算法,灰狼群一般分为四个等级,如图1所示。

图1 狼群社会等级结构
α、β、δ分别代表狼群的三个首领,ω则表示狼群的普通成员,它们的等级依次降低,等级高的狼对等级低的狼对等级低的狼有绝对的领导权,在头狼的领导下狼群不断更新位置,不断靠近猎物。
1.2 GWO的数学模型
在n维的空间中,灰狼α的位置为Xα(Xα,1,Xα,2,Xα,3,…,Xα,n),灰狼β的位置为Xβ(Xβ,1,Xβ,2,Xβ,3,…,Xβ,n),灰狼δ的位置为Xδ(Xδ,1,Xδ,2,Xδ,3,…,Xδ,n),灰狼捕食过程的位置变化可以用下面的数学公式表示:

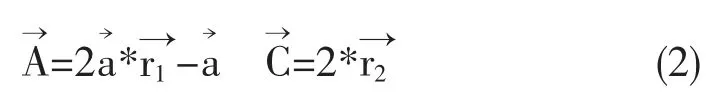
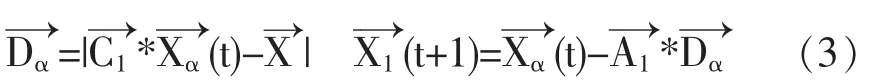
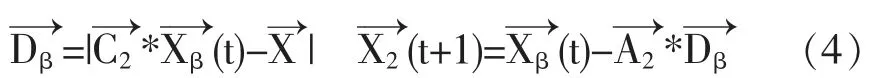
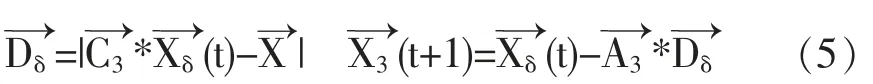
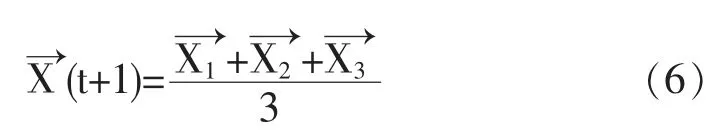
1.3 LightBGM算法
LightGBM是由微软研发基于决策树算法的高性能、分布式的梯度提升框架。LightGBM可以看作是GBDT的加强版,在不降低精度的情况下,不仅减少了运行时间、提高训练效率,而且降低了内存的使用。
1.3.1 Histogram算法
直方图算法利用分桶的思想把连续的特征离散为k个整数特征,并构造一个宽度为k且含有k个bin的直方图,在遍历时,不需要直接遍历数据,而是通过遍历k个bin来获取最佳分裂点。在计算特征分裂增益时,预排序方法每次遍历特征都要计算该特征的增益,而直方图算法只需计算k次,可以有效地降低时间复杂度。
1.3.2 基于GOSS的数据处理
由于目标函数的增益大部分来源于梯度绝对值较大的样本,梯度小的样本对目标函数的贡献相对较小,全部计算的话效率不高,但是直接抛弃梯度小的样本数据,会改变样本数据的分布,进而降低预测模型的准确率。而LightGBM通过使用单边梯度抽样算法(GOSS)对样本进行抽样,GOSS对梯度较大的样本会全部保留,对梯度较小的样本则采取随机抽样的方式,为了不让数据分布影响最终模型的准确率,在计算目标函数的增益时,GOSS会引入了一个常量乘法器进行平衡,过程如图2所示。
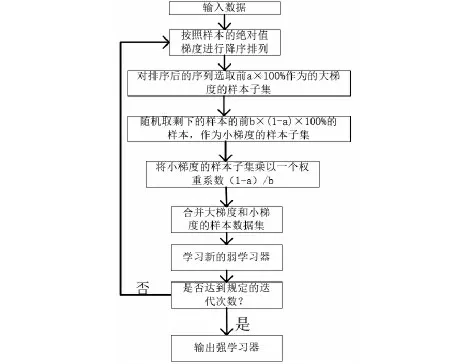
图2 基于GOSS的数据抽样
1.3.3 基于(Leaf-wise)的叶子生长策略
大多数GBDT工具在树的生长过程中使用按层(level-wise)的生长方式,即使处于同一层的某些叶子节点的分裂增益很低,level-wise仍然不加以区分地将它们进行搜索,虽然不容易过拟合,却增加了很多不必要的运算。而使用Leaf-wise的生长策略只需要分裂增益效果最好的那个节点,减少了运算,但是为了防止过度拟合,应该设置一个最大树深加以限制。
1.3.4 EFB算法
在某些应用场景下,数据集可能会出现大量的稀疏特征,即少部分不为零,大部分为零的特征,通常我们认为这些特征是互斥的(不会同时取非零值),LightGBM通过使用EFB将一些互斥特征进行融合绑定,从而减少特征数量,增加计算速度。由于本文的数据并不涉及这方面的问题,故在此不过多叙述。
1.4 GWO-LightBGM模型
LightBGM因其高效的计算能力被广泛地应用在分类,回归等机器学习任务中,但是在实际使用LightBGM做预测时,涉及众多超参数的设置,而这些超参数又直接影响模型的预测精度。因此,为了快速提高LightBGM的预测准确率,本文引入灰狼优化算法对LightBGM的几个重要超参数(learning_rate、n_estimators、num_leaves、max_depth),进行快速择优,建立GWO—LightBGM预测模型,流程如图3所示。
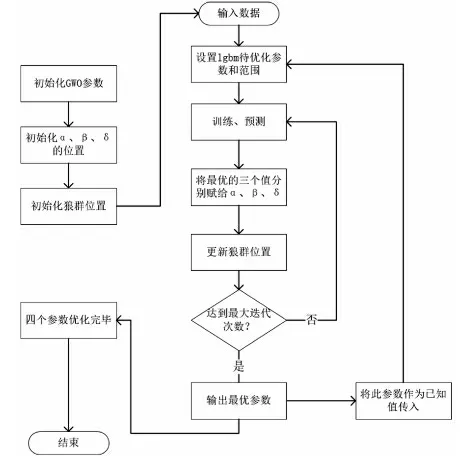
图3 基于GWO-LightGBM的流程图
建立GWO—LightBGM模型的主要步骤为:
步骤一:筛选出对LightBGM预测精度影响比较大的四个超参数。
步骤二:设置灰狼算法的参数,如狼群数量,最大迭代次数等。
步骤三:初始化α、β、δ和狼群的位置。
步骤四:引入样本数据集,设置LightBGM待寻优的参数,并且设置寻优的范围。
步骤五:计算灰狼个体的适应度,将适应度最高的三个值分别进行保存,
步骤六:将最优的三个值分别设置为Xα,Xβ,Xδ,并且根据公式(3)~(8)更新狼群的位置。
步骤七:判断是否满足终止运算条件,不满足则返回步骤五,如果满足则进入步骤八。
步骤七:将输出的参数作为先验信息传入步骤四,并设置下一个待寻优的参数和范围。
步骤八:将得到的四个参数代入LightBGM算法中,输出预测结果。
2 实验数据及评价指标
2.1 冲击地压预测指标和危险等级的确定
在煤矿开采工作当中,因为冲击地压往往发生突然、征兆不明显,且冲击地压又是由于多种因素共同导致的。因此,确定主要的影响因素、选取合适的预测指标是正确预测冲击地压所必须的条件。
结合国内外相关研究文献和实例分析,本文选取四个影响冲击地压的关键指标,分别是:Wet:岩石的弹性变形能量指数、σθ:围岩切向应力、σθ/σc:围岩的切向应力和单轴抗压强度的比值、σc/σt:岩石脆性指数。
根据冲击地压发生时的特征以及参考其他相关研究文献,本文将冲击地压的评价结果分为4个等级[10]:Ⅰ级:无冲击地压危险,Ⅱ级:弱冲击地压危险,Ⅲ级:中等冲击地压危险、Ⅳ级:强冲击地压危险。
为验证GWO—LightBGM预测模型的可行性,本文根据相关文献[11,12],收集到国内外多个矿区共计67组历史真实数据,其中无冲击地压危险的样本数据为12条,弱冲击地压危险的样本数据为12条,中等冲击地压危险的样本数据为29条,强冲击地压危险的样本数据为14条,样本数据并无缺失值,部分样本数据如表1所示。
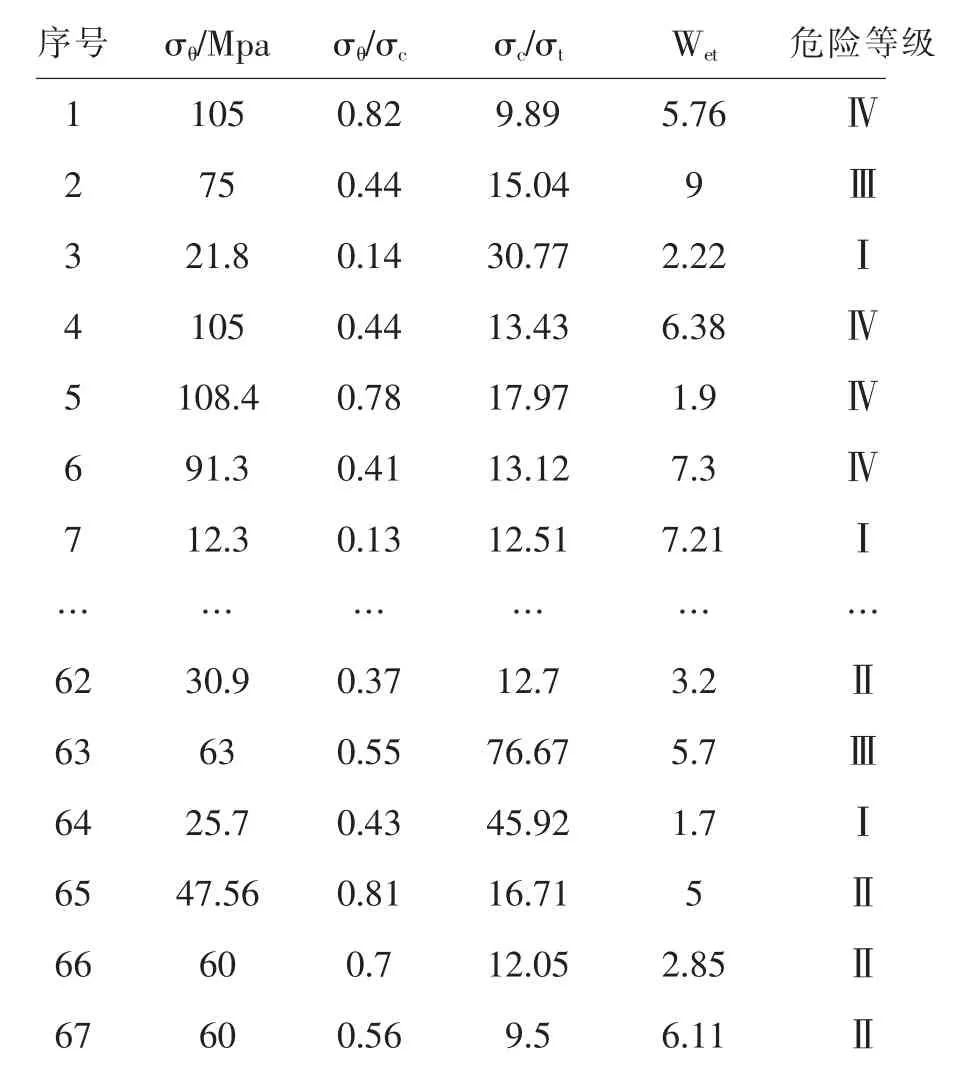
表1 部分样本数据表
2.2 评价指标的选取
为了多方面综合的评价模型的预测性能,本文选取三个用于评价该模型的指标。分别是准确率,均方根误差和杰卡德系数。
其中均方根误差(RMSE)可以用来衡量预测值与真实值之间的差异,计算结果越小,代表预测的精度越高,反之则表示预测的精度越小。计算如公式(7)所示:
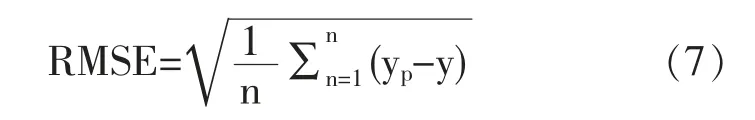
其中yp代表预测值,y代表真实值,n表示预测次数。
杰卡德系数(JaccardIndex)也称为杰卡德相似系数,可以用来描述两个集合之间的相似度[13],与均方根误差不同的是,杰卡德相似系数计算布尔值度量的个体之间的相似度而不计算差异具体值的大小,也就是说它只关心个体之间具有的特征是否一致。杰卡德系数越大,说明相似度越高,杰卡德系数越小,说明相似度越低。因此,如果把真实冲击地压等级定义为集合A,把预测等级定义为集合B。杰卡德相似系数可用公式(8)来表示:
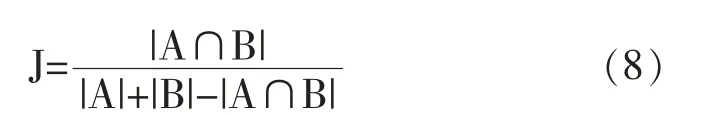
3 实验结果与分析
将样本数据按照8:2的比例分别划分成训练集和测试集[14],使用GWO-LightGBM模型对数据进行预测,为了比较说明,文章中还使用了XGboost和SVM在相同样本的基础上分别进行了预测。由于LightGBM和XGboost都是基于树形结构的算法,因此不需要对于数据进行无量纲化处理,而支持向量机(SVM)属于线性模型,一旦特征值相差较大就会影响模型的性能,因此在使用SVM作预测时,需要按照公式(9)进行标准化处理。

其中xi代表原始数据,表示样本的平均值,s表示样本的标准差。
在使用GWO-LightGBM作预测时,部分参数设置如下:灰狼种群数量为20,最大迭代次数为100,num_leaves的 搜 索 范 围 为[20,50],max_depth的搜索范围为[3,10],n_estimators的搜索范围为[50,500],learning_ratede搜索范围为[0.01,0.3]。当模型达到最大迭代次数后,运算得到num_leaves的值为39,max_depth的值为6,n_estimators的值为85,learning_ratede的值为0.062,将得到的4个参数值代入LightGBM预测模型中预测结果如图4所示。
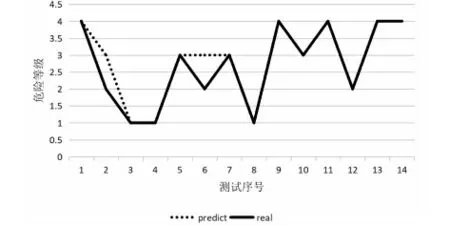
图4 GWO-LightGBM预测结果
从图4可以看出,在14组测试样本中,只有第二组和第六组预测结果有误,其他12组数据均与实际情况完全符合,模型的预测准确率为85.7%,说明GWO-LightGBM在预测冲击地压时,有着良好的效果。
为了突出该模型的优越性,将GWO-Light-GBM,XGboost和SVM的预测结果和评价指标综合作比较,结果如表2和表3所示。

表2 不同模型的预测结果
表2展示的是三个预测模型对14组测试数据的详细预测结果,从中可以看出,支持向量机对于小样本冲击地压数据的预测效果最差,14组测试样本中,预测错了4组。XGboost的预测效果优于SVM,仅在第2、6、7组数据 预测错 误。GWOLightGBM的预测效果最好,只在第2和第4组数据预测错误。
表三展示的是三个预测模型在不同评价指标上的表现结果,从数据中可以得出,无论是准确率、均方根误差还是在杰卡德系数的比较上,GWOLightGBM的评价结果都明显优于XGboost和SVM。因此可以说明,GWO-LightGBM在对非线性、小样本的冲击地压预测中,预测效果良好。
4 结论
针对传统调参方式存在的问题,本文引入灰狼优化搜索算法对LightGBM的超参数进行快速择优,简化了调参的过程。将GWO-LightGBM应用于冲击地压的预测中,并与传统的XGboost和SVM进行比较,结果表明GWO-LightGBM模型在面对非线性和小样本的冲击地压的预测时,GWOLightGBM无论在准确度、均方根误差和杰卡德系数方面,均明显高于其他两个模型。本文使用的GWO-LightGBM模型在对小样本的冲击地压作预测时,有一定的优势。但是在给大样本数据的冲击地压作预测时,参数的搜索时间会变长,有待于进一步优化。

