BDS-3、BDS-2/BDS-3融合双频信号精密单点定位精度分析
卢福康,肖星星,魏 民,刘金涛
(1.安徽理工大学 空间信息与测绘工程学院;2.安徽理工大学 矿区环境与灾害协同监测煤炭行业工程研究中心;3.安徽理工大学 矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽 淮南 232001)
引言
全球卫星导航定位系统 (Global navigation satellite system,GNSS)可向全球提供高精度的定位服务,授时服务,已成为空间信息基础设施重要的组成部分,已是在强国和强军的建设发挥着十分重要的作用。按照“三步走战略“,我国的北斗导航系统(BeiDou navigation satellite system,BDS)已从BDS-1的双星定位系统发展到BDS-2区域导航定位系统,最后到建设完成BDS-3全球定位系统。2020年7月31号BDS-3卫星系统正式宣布开通,联合BDS-2为全球提供高精度、高质量的定位、导航、授时服务。BDS-2和BDS-3均是混合星座,都包含了3个类型的星座,分别是地球静止轨道(geostationary earth orbit,GEO)卫星、中圆地球轨道(medium earth orbit,MEO)卫星、倾斜地球同步轨道(inclined geosynchronous orbit,IGSO)。BDS-2卫星星座由15颗卫星组成,分别包含5颗GEO、有3颗MEO和7颗IGSO在轨运行卫星;BDS-3卫星星座由30颗卫星组成,分别包含3颗GEO、3颗IGSO、24颗MEO[1-4]。对比BDS-2和BDS-3,BDS-3采用了更多轨道低、定轨精度高,卫星的空间几何结构变化快的MEO卫星,这样有利于提高定位精度和收敛时间[5,6]。
随着我国BDS-3系统正式组网并正式宣布开通,关于BDS定位性能质量有了大量的研究,文献对BDS-3的单双频及不同信号进行了质量分析,实验表明双频加入BDS-2系统后,定位精度提升不明显,但收敛速度有了提升;单频BDS-3的B1C定位信号最优,与GPS L1信号在同一水平上[7],文献对BDS-3进行在不同的高度角下的伪距单点定位分析,研究结果表明,BDS-3 SPP的定位精度先增加后降低,最优的定位精度在高度角20°时达到最优,但没有对BDS-3的定位精度进行分析[8],文献[9]对BDS-3的定位服务性能进行了综合分析,在不同的定位模式下,BDS-3/BDS-2与BDS-2相比,在收敛时间上有所提升,但在定位精度上没有太大的提升[9],对BDS-3新频点信号的测距精度和定轨精度分别进行了分析和评估,结果表明,BDS-3新信号B1C&B2a测距多经误差分别为0.43、0.24m,测站坐标静态精密单点定位精度达到0.025m[10],上述参考文献大都都是对BDS-3的定位精度进行分析,对BDS-2/BDS-3融合定位性能的方面研究较少,大都都是忽略了系统之间的误差,由于BDS-2和BDS-3信号的调制方式不同,即使在频率相同的情况下,两者也存在不同,所以就会造成BDS-2信号系统和BDS-3信号系统存在系统性偏差ISB(inter-system bias)[11]。
鉴于当前的研究,由于传统的无电离层组合,虽然消除了电离层误差的影响,但是也造成了观测误差和其他误差的放大,因此本文采用非差非组合的函数模型进行解算,对于BDS-2/BDS-3之间的ISB采用白噪声估计,先对PPP定位原理和处理策略简单介绍,重点对BDS-3系统、BDS-2/BDS-3融合系统进行精密单点定位精度和收敛时间进行分析。
1 PPP函数模型
一般地,接收机r接收到卫星Q发出的频率(i=1,2)组成的非差非组合伪距和载波观测值表达式为:
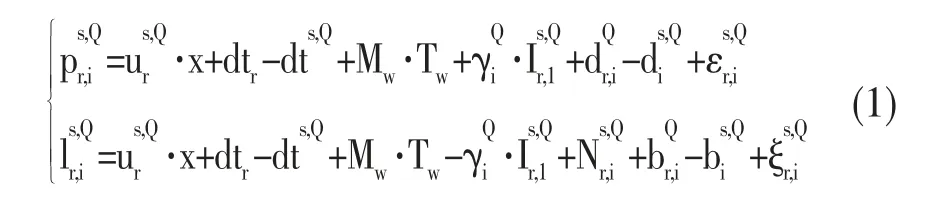
由于BDS-2与BDS-3之间存在系统性误差,也叫时间延迟误差,因此加上一个时间延迟偏差参数ISB,同时引入GPS接收机钟差作为参考,另外也要考虑所下载的精密钟差存在通过双频无电离解算所吸收的伪距硬件延迟,即又其中可同时被接收机钟差和电离层参数吸收,可通过列方程组解得,接收机吸收部分为。再加入卫星差分码偏差(DCB)改正,得到最终的非差非组合函数表达式为:
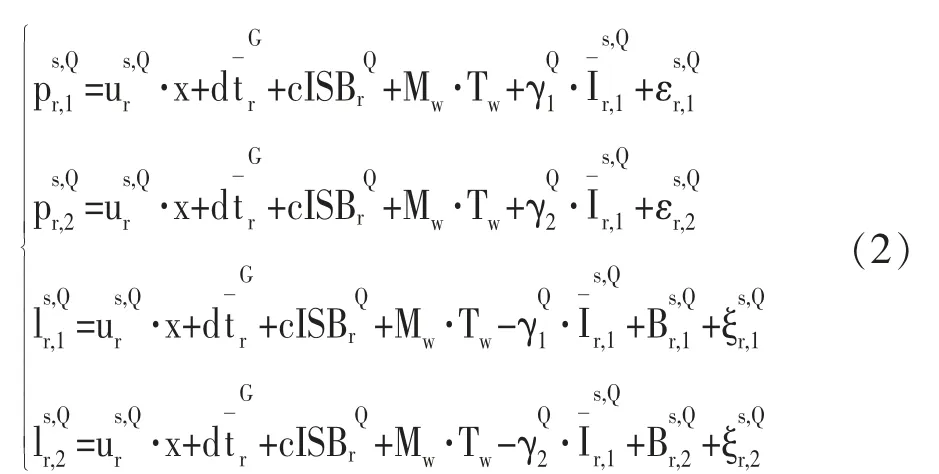
其中
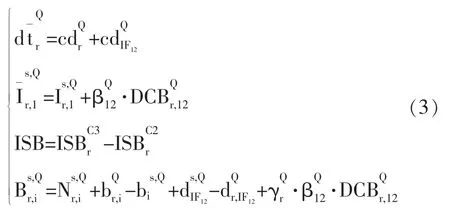
2 随机模型
在对GNSS进行PPP定位时,不仅要考虑函数模型,还要考虑随机模型的选择,在PPP中比较常用的时高度角随机模型和信噪比随机模型。本文采用的时高度角随机模型,其原理是构建高度角E和测量噪声σ2之间的函数关系,其通用公式为:

式中E为卫星高度角,a和b是常数,值均为0.003。
3 数据来源和数据处理策略
本文的实验数据是来源MGEX(multi-GNSSexperiment,MGEX)数据中心下载的观测数据,采取的2021年积日57-63共7天的观测数据进行实验分析,测站的分布见图1,其他精密产品均来自武汉大学IGS中心。在数据处理过程中,BDS处理采用的频率是B1I和B3I,试验分析采用的是静态和仿动态两种PPP解算方式,静态和动态PPP的坐标参数解算方式分别为常数估计和白噪声估计,精度验证是通过解算的结果与IGS所下载snx文件周解值比较,然后分析三个方向E(east)、N(north)、U(up)的定位精度和收敛时间。收敛时间的依据是根据各个方向定位误差达到0.1m并且在稳定在20个历元所需要的时间,并将三个方向收敛后的定位精度的均方根(root mean square,RMS)作为定位误差的统计值。PPP主要的处理策略如表1所示。
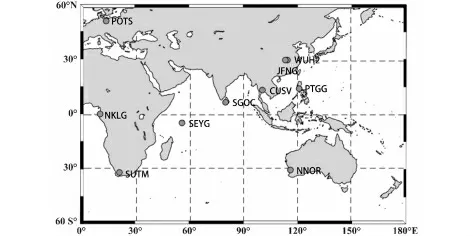
图1 选取的10个MGEX测站分布

表1 PPP处理策略
4 BDS-3、BDS-2/BDS-3双频PPP定位性能分析
本节对BDS-3、BDS-2/BDS-3不考虑ISB及考虑ISB的PPP静态和动态进行定位精度和收敛时间进行对比分析。
4.1 PPP静态定位性能分析
随机选取了3个测站CUSV、JFNG、WUH2年积日为57天的进行了分析。对3个测站画出了BDS-3、BDS-2/BDS-3不考虑ISB及考虑ISB的静态PPP定位误差、可用卫星数及对应的PDOP值,见图2和图3。可用卫星是指如果该卫星参与了PPP模型的解算,则认为该卫星可用。对于定位结果可以看出,BDS-2/BDS-3的可用星数比BDS-3可以卫星数明显增多,使得其PDOP值明显降低,表明BDS-2/BDS-3卫星空间分布结构比BDS-3卫星系统空间分布结构好,使得其定位精度和收敛时间有明显得提高,3个测站在E、N方向上,BDS-2/BDS-3卫星系统比BDS-3卫星系统能在较短的时间内收敛到很小的定位精度,之后的历元定位精度误差相当,在U方向可以明显看出在整个历元,前者的定位精度高。对比3个测站而言,CUSV测站和JFKG测站的可用卫星数相当,但CUSV测站1100历元之后有1小段的PDOP值较差,导致定位误差有一点略微上升,其他时候两测站的定位精度相当,与WUH2测站相比而言,前者可用卫星数比之高,WUH2测站的BDS-3卫星系统的PDOP值较差,使得其定位精度较差,尤其在U方向上,定位精度整体比前面两个测站的定位精度差。对于BDS-2/BDS-3考虑ISB而言,定位精度有一定的提高,但不明显,收敛时间提升不大。
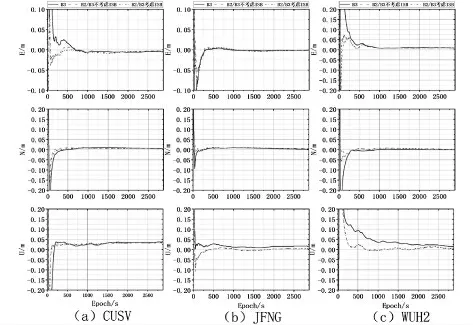
图2 3个测站BDS-3、BDS-2/BDS-3不考虑ISB及考虑ISB的静态PPP定位误差序列图
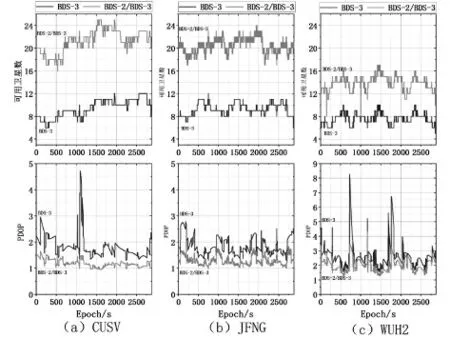
图3 3个测站可用卫星数及PDOP值图
对10个测站7天的观测数据进行PPP解算,表2给出了BDS-3、BDS-2/BDS-3不考虑ISB及考虑ISB的PPP静态定位误差和收敛时间统计结果。可以看出,BDS-3卫星系统的PPP各个方向的收敛时间和定位精度低于BDS-2/BDS-3卫星组合系统,对于考虑BDS-2/BDS-3卫星系统的ISB后,三个方向的收敛时间和定位精度有了一定程度上的提升。BDS-2/BDS-3卫星系统较BDS-3卫星系统,在E、N、U三方向上,收敛时间分别提升了20.8%、32.5%、17.9%,定位精度分别提升了3.7%、8.0%、5.9%。对于BDS-2/BDS-3加入考虑ISB后,在E、N、U各个方向上,收敛时间分别提升了12.2%、12.1%、8.6%,定位精度分别提升了8.3%、4.4%、2.6%。

表2 10个测站静态PPP收敛时间和收敛后定位精度统计表
4.2 PPP动态定位性能分析
图4给出了3个测站CUSV、JFNG、WUH2的BDS-3、BDS-2/BDS-3及考虑ISB的卫星系统的动态PPP一天的定位误差序列。可以看出BDS-3卫星系统定位精度和收敛时间没有BDS-2/BDS-2组合卫星系统的高,从3个测站的定位误差序列可以看出,在E、N方向上明显比U方向上的定位精度高,且比U方向定位误差稳定,对CUSV和WUH2测站进行分析,结合图3和图4,在CUSV测站1100历元左右和WUH2测站的760、1300、1800历元,可以明显分析出当卫星系统的PDOP值上升时,定位精度会有明显的降低,特别在U方向上,定位精度浮动较大,可以看出PDOP值对U方向的定位精度更敏感,加入BDS-2系统后,两测站的卫星空间结构有了明显的提高,使得PDOP值异常的地方有了明显的改善,定位精度有了明显的提高,对CUSV、JENG与WHU2测站进行对比分析,也可以看出前者的PDOP值更低,说明卫星得空间结构好,使得定位精度高。对于BDS-2/BDS-3卫星系统加入考虑ISB后,可以看出收敛时间和定位精度有一定程度上得提升。

图4 3个测站BDS-3、BDS-2/BDS-3不考虑ISB及考虑ISB的动态PPP定位误差序列图
对10个测站7天的观测数据进行PPP动态解算,表3给出了BDS-3、BDS-2/BDS-3不考虑ISB及考虑ISB的PPP动态定位误差和收敛时间统计结果。可以看出BDS-3的动态PPP解算定位解算结果比BDS-2/BDS-3卫星定位系统精度低,对BDS-2/BDS-3卫星组合系统加入ISB考虑之后,三个方向的收敛时间和定位精度有了一定程度上的提升。BDS-2/BDS-3卫星组合系统比BDS-3卫星系统,在E、N、U三方向上,收敛时间分别提升了21.6%、41.9%、37.2%,定位精度上分别提升了3.3%、10.5%、3.4%,在加入考虑ISB之后,收敛时间分别提升了18.6%、17.1%、3.9%,定位精度上E、N方向上分别提升了6.3%、6.5%,U方向上的定位精度相当。

表3 10个测站动态PPP收敛时间和收敛后定位精度统计表
4.3 BDS-2/BDS-3系统偏差ISB
BDS-2和BDS-3由于调制方式和信号频率的不同会导致接收机接收信号的延迟有所不同,因此BDS-2与BDS-3之间存在一定的系统偏差ISB参数,通过解算,给出来3个测站CUSV、JFNG、WUH2的ISB的时间序列图,如图5所示,可以看出3个测站ISB的变化趋势总体来说是相差不大的,CUSV和JFNG测站变化趋势是一致的,只是总体上存在差异,最大差异在4.8ns。
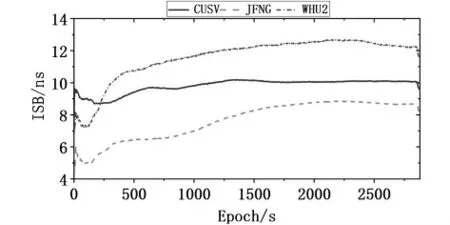
图5 三个测站一天ISB时间序列图
图6给出了10个测站7天天内的ISB的STD(Standard Deviation)的时间序列图来衡量其稳定性,图7给出了10个测站BDS-2/BDS-3的ISB的7天间的STD平均值。可以看出,10个测站中有大部分测站的ISB天内整体上有较好的稳定性,天与天之间,每个测站整体上表现差异不是很大,只有在一定程度上下波动,综上所得,BDS-2/BDS-3的天内大部分测站STD在0.25ns~1.0ns范围内,个别也在2.0ns内,说明天内具有较好的稳定性,天与天每个测站的STD都表现在同一个水平上,说明天与天之间的稳定性较好。
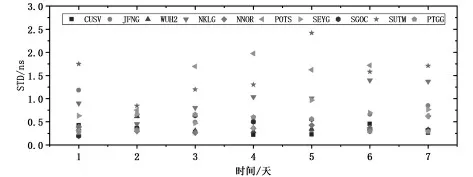
图6 10个测站天内的STD平均值
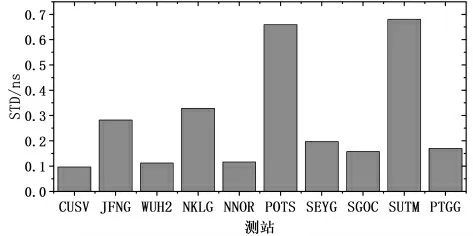
图7 10个测站天间的STD平均值
5 总结
本文基于MGEX测站的数据中心实测北斗观测数据,选取10个测站对BDS-3卫星系统、BDS-2/BDS-3组合卫星系统及考虑ISB的组合卫星系统,采用非差非组合函数模型对其双频静态和仿动态PPP定位性能进行分析,得出以下结论。
(1)测站观测到的卫星数越多,其PDOP值就越小,表明该测站的卫星空间分布越好,能够提高定位精度和收敛时间。因BDS-2/BDS-3卫星系统比单BDS-3卫星系统有更多的可用卫星数,其PDOP值异常部分,得到了有效的改善,使得BDS-2/BDS-3卫星系统比BDS-3系统定位精度高,BDS-2/BDS-3之间的ISB的天内和天间的STD的稳定性表现良好。
(2)BDS-3卫星系统PPP定位性能分析得出,在静态模式下,在E/N/U各个方向上的收敛时间分别为57.0/25.8/46.3min,收敛后的定位误差精度能够达1.86/1.23/3.21cm,在动态模型下,在E/N/U三个方向上的收敛时间分别为106.8/51.2/91.8min,收敛后的定位误差精度能够达到3.03/2.56/4.64cm;BDS-2/BDS-3卫星组合系统定位性能分析得出,在静态模式下,在E/N/U各个方向上的收敛时间分别为45.1/17.4/38.0min,收敛后的定位误差精度能够达到1.79/1.13/3.02cm,在动态模式下,在E/N/U三个方向上的收敛时间分别为83.7/29.7/57.6min,收敛后的定位误差精度能够达到2.93/2.29/4.48cm。
(3)对于BDS-2/BDS-3组合系统加入考虑ISB参数估计后,可以得出在静态模式下,在E/N/U各个方向上的收敛时间分别提升了2.2%、12.1%、8.6%,定位精度分别提升了8.3%、4.4%、2.6%,动态模式下,收敛时间分别提升了18.6%、17.1%、3.9%,定位精度上E、N方向上分别提升了6.3%、6.5%,U方向上的定位精度相当。

