高速公路应急救援资源调度管理策略研究

谭中楠,曹明月,郭 飞

(1.河南省交通运输发展集团有限公司郑州分公司,河南 郑州 450000；2.河南北斗卫星导航平台有限公司,河南 郑州 450003)

0 引言

近年来,以计算机、网络、通信、大数据、物联网等技术为支撑[1-3],高速公路智能管理系统[4-5]得到了迅速发展。然而,直到目前为止,我国公路管理水平与事故处理速度仍无法满足人们的需求,道路拥堵和交通事故频发现象十分严重。

为此,有研究将物联网、云计算引入智能交通系统[6-7]，从而改善高速公路信息收集不准确和未及时反馈的问题。文献[8]基于物联网技术对隧道洞口结冰动态监测技术进行研究。文献[9]设计了基于故障状态演化的高速公路机电设备智能维护系统,实现高速公路机电设备故障检测。文献[10]基于深度学习方法搭建了高速公路智能监控分析平台。然而,上述研究主要是对历史数据进行分析,对事故处理及资源调度等方面的研究较少。目前,在解决突发事件应急资源调度方案的构建问题时,主要采用优化建模方法。主流的优化建模方法有分层序列法[11]、遗传算法[12-13]等。然而,目前多目标优化算法在处理3个以上的目标函数时仍存在很多问题。首先,优化目标数量的增加导致种群中非支配解的比例增加,从而降低求解效率；其次,在高维目标空间中,保持多样性指数的计算复杂度过高；最后,在高维对象空间的情况下,复合算子的搜索效率较低。

考虑到高速公路资源调度管理时效性要求,本文将处理高速公路应急事件资源调度问题转化为多目标优化问题,并提出利用改进的多目标优化算法实现资源的最优调度方案。该方案充分结合非支配排序遗传算法(non-dominated sorting gentic algorithm,NSGA-Ⅲ)和高斯估算法优点，可有效解决高速公路应急处理与资源调度多目标优化问题。

1 处理与资源调度建模

考虑到高速公路紧急情况发生的不确定性,这些应急事件可能发生在多个地点。同时,由于紧急情况的关联性,如极端事件(暴雪、台风、地震、洪水等),可能使许多潜在地点受到影响。因此,需要考虑灾难现场和潜在灾难现场的共同需求。这也导致资源调度模型的多目标优化特性。为最大化满足高速公路灾难现场和潜在灾难现场资源调度需求，本文研究以最小化调度时间、调度成本、灾难现场损失和最小化潜在灾难现场不满意度为目标函数,建立高速公路多目标优化模型。因此,该资源调度模型能够最大程度地满足现实生活中应对突发事件的需求。

1.1 相关假设

为简化计算,本文作如下假设。

①本文只考虑从1个救援站点到多个灾难站点和多个潜在灾难站点的场景。

②已知从救援现场到每个灾难现场的距离和资源调度的速度。

③每个灾难现场对不同资源的需求是已知的。

④在调度过程中,灾难现场的调度成本和每个资源的损失是已知的。

1.2 优化模型

资源调度模型目标函数如式(1)所示。

(1)

式中：f1(X)为最小化调度时间目标函数；f2(X)为最小化调度成本目标函数；f3(X)为最小化灾难现场损失目标函数；f4(X)为最大化潜在灾难现场满意度目标函数。

式(1)显示了应急资源调度模型的总体优化目标。

(2)

式中：R1,R2,…,Rr为r个可调度的资源；N1,N2,…,Nn为n个灾难现场；ti(i=[1,N])为第i个资源的单位调度时间；Xik为救援点向第i个灾难现场分配的第k个资源量；Di为从救援点到第i个灾难现场的距离；vi为从救援点到第i个灾难现场的资源调度速度。

(3)

式中：ci(i=[1,N])为第i个资源的单位调度成本。

(4)

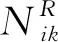
(5)

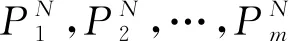
约束条件为：

(6)

(7)

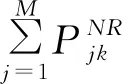
2 结合NSGA-III和高斯估计的混合进化算法

2.1 算法思路

NSGA-III在高维目标空间中具有明显优势。NSGA-III使用广泛分布的参考点来维持群体中个体的多样性。在优化目标构建的超平面中选择个体时,使用理想点和参考点之间的连接,即从理想点和参考点组成的直线中选择最近的个体。然而,NSGA-III使用传统的交叉变异算子在父种群中随机选择个体。这种操作显然只考虑个体的局部特征。因此,本文设计了1种结合NSGA-III和高斯估计的混合进化算法。混合算法在每个种群中选择非优势个体计算总体特征,并使用高斯估计算法生成新一代种群。这可以大大提高最优解的搜索效率和准确性。

令父种群为Pt,首先计算总体的适应度函数Ft。

Ft=[f1(Pt),f2(Pt),f3(Pt),f4(Pt)]

(8)

式中：fi(i=1,2,3,4)为第i个目标函数的适应度函数。

其次,对各个适应度值执行非支配排序操作。然后,对排名最高的个体计算其高斯分布均值和协方差。再次,通过高斯分布生成后代个体。接着,对新生成的个体执行变异操作。最后,使用父种群Pt和后代个体Gt计算最小适应度函数Zmin。最小适应度函数计算如式(9)所示。

(9)

进一步,对Gt和Ft进行非显性排序,使用生成的参考点和最小适应度值Zmin进行个体选择,以获得子种群Pt+1。

混合进化算法流程如图1所示。

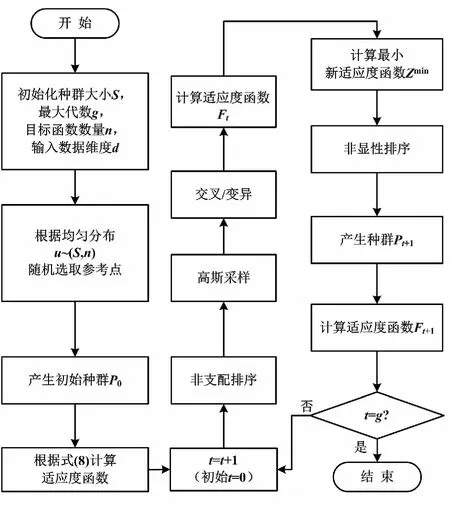
图1 混合进化算法流程图

混合进化算法流程的主要阶段包括交叉遗传算子和时变高斯变异。图1中：t为迭代步长；g为最大迭代次数。

2.2 优化策略

2.2.1 交叉遗传算子

遗传算子对于控制进化算法的优化过程具有重要意义。在本小节中,交叉和变异算子将应用于创建与初始种群大小相同的新种群。首先,随机挑选来自第t代的2个父代x1(t)和x2(t),并使用模拟二进制交叉技术执行交叉操作,从而产生2个子代x1(t+1)和x2(t+1)。

(10)

式中：γ为扩展因子,表示子代与父代绝对差异的比率。

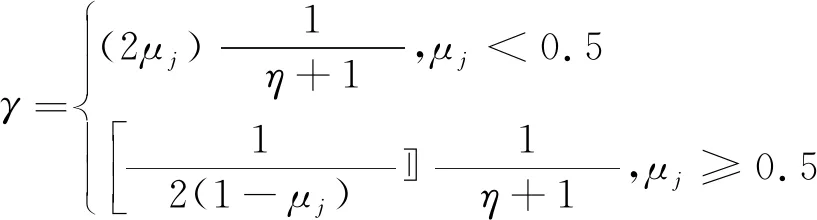
(11)

式中：μj为随机参数,且μj∈(0,1)；η为固定参数,通常取1。

2.2.2 时变高斯变异

在求解多目标优化问题时,传统NSGA-III可能会使种群过早陷入局部最优,并失去多样性。因此,为了提高解的质量,还可以增强算法的鲁棒性。本小节设计了1种时变高斯变异函数,通过变异算子产生新的种群。具体思路是在每一代对一些最差的个体使用高斯变异。一维高斯密度函数rg(x)定义如式(12)所示。

(12)

式中：μ和σ分别为高斯密度函数的均值和标准差,通常取μ=1、σ=0.5。

所提混合进化算法中,时变高斯变异函数计算如下。

(13)

式中：Pm为变异概率；rg为服从平均值为0、方差为1的高斯分布；Vu和Vl为决策变量的上界和下界；Mr为变异参数,本文取值为0.5；t为迭代次数；T为最大迭代次数。

3 仿真与分析

3.1 仿真环境

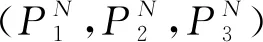
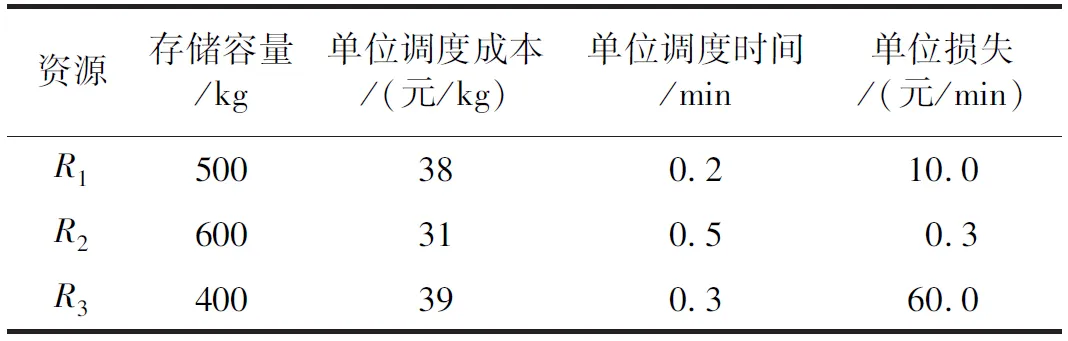
表1 救援站点对各资源参数

表2所示为灾难点/潜在灾难点对各资源需求。

表2 灾难点/潜在灾难点对各资源需求

同时，救援站点与灾难点相关参数如下：救援站点与灾难点1的距离为453 m，与灾难点2的距离为411 m，与灾难点3的距离为107 m，与灾难点4的距离为111 m。潜在灾难点灾难发生概率参数如下：潜在灾难点1灾难发生概率为0.65，潜在灾难点2灾难发生概率为0.23，潜在灾难点3灾难发生概率为0.38。试验场景相关参数信息设置如下：初始种群大小为700，最大迭代次数为150，交叉率为0.1，变异率为0.01。

3.2 性能对比与分析

图2所示为不同算法目标函数对比结果。由图2可知，传统NSGA-III将在第120代左右收敛,所提混合算法将在40～110代收敛到最优解。仿真结果表明,混合进化算法与NSGA-III相比性能更优,运算效率提升9%～200%。因此,所提算法性能优于传统NSGA-III。仿真结果进一步验证了本文方法对高速公路应急事件管理具有一定的借鉴作用。

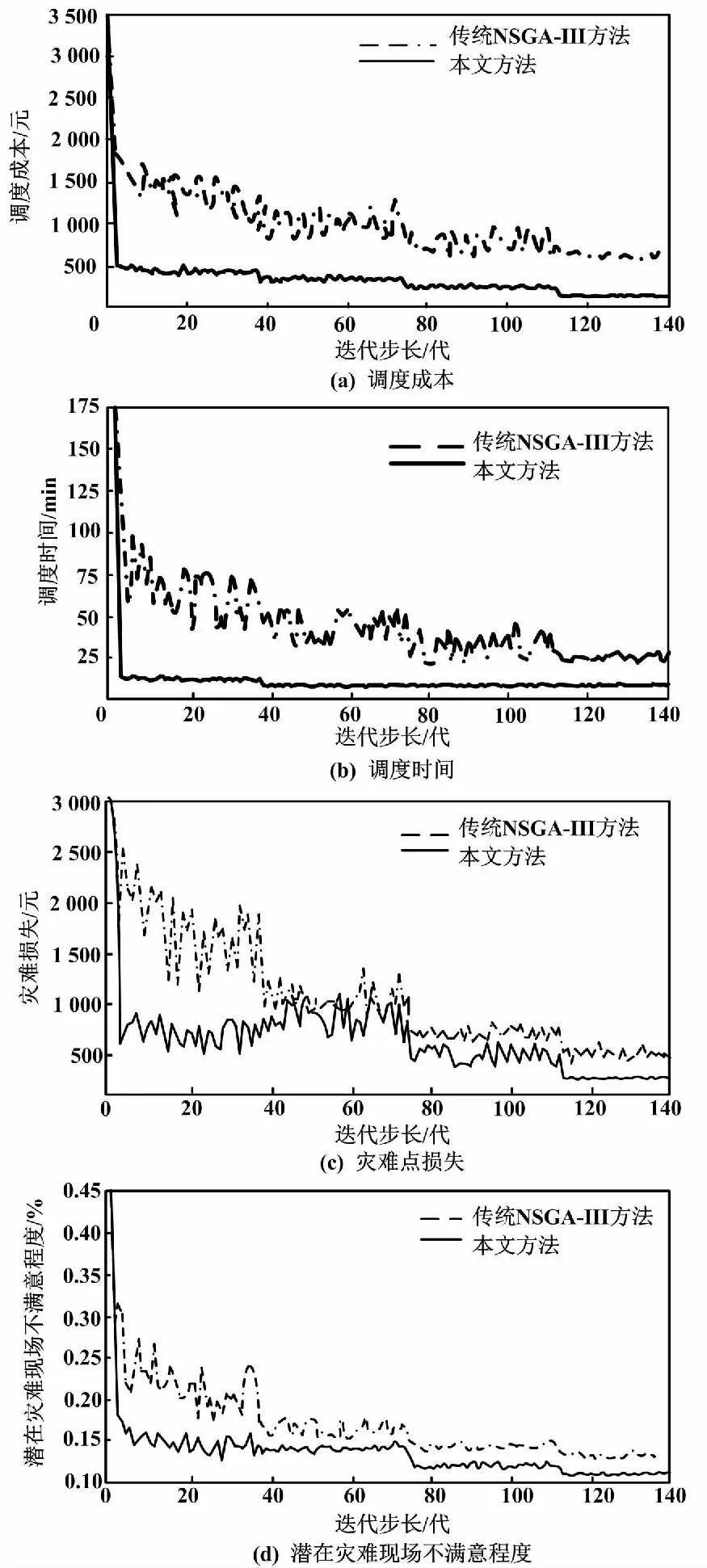
图2 不同算法目标函数对比结果

4 结论

本文对高速公路应急处理进行了研究与分析,提出了一种高速公路应急救援资源调度管理策略,实现应急事件资源调度。为查找最优资源调度方案，本文提出了混合进化算法，建立调度时间最优、调度成本最优、灾难站点损失最小、潜在灾难现场不满意程度最小的4目标资源调度优化模型。本文方法对高速公路应急事件管理具有一定借鉴作用。未来工作可对分布式节点计算进行研究,从而进一步提升调度效率。