京津冀地区NOx和VOCs协同减排成本及减排策略研究

李晓瑜，王 念，刘慧文，张增凯

1. 天津大学管理与经济学部，天津 300072

2. 厦门大学环境与生态学院，福建 厦门 361102

近年来，我国通过实施《大气污染防治行动计划》等一系列污染防控措施，空气质量水平整体上出现了改善. 但是，京津冀地区作为我国大气污染防治的重点区域，其污染形势依然十分严峻[1-2]. 2019年，我国城市环境质量最差的5个城市中有3个位于京津冀地区，分别为石家庄市、邯郸市和唐山市，且京津冀PM2.5年均浓度下降比例仅为1.7%，O3年均浓度上升比例高达7.7%，升幅高于其他重点污染区域(长三角地区和汾渭平原等). 此外，京津冀及周边地区PM2.5和O3超标天数占总超标天数的比例分别为42.9%和48.2%，大幅高于其他污染物超标天数占比. 因此，为打赢“大气污染防治攻坚战”，提升人民的蓝天幸福感，需要高度重视PM2.5和O3的协同治理[3].

研究[3-6]表明，PM2.5和O3主要来源于二次转化，而二次转化的共同前体物为NOx和VOCs. 相比于单独控制PM2.5，协同控制NOx和VOCs的排放，对于京津冀地区PM2.5和O3协同治理更具可取性和重要性[7-9]. 由于PM2.5和O3与NOx和VOCs的转化关系非常复杂，不合理的减排比例甚至会造成污染物浓度的升高，因此如何确定NOx和VOCs的具体减排比例，以实现京津冀地区PM2.5和O3浓度的协同达标，是目前大气污染联防联控政策制定的一项艰巨任务和挑战.

随着大气污染协同治理的重要性逐渐凸显，越来越多的学者开始关注污染物的协同控制. 目前关于温室气体和大气污染物之间协同控制的研究较为丰富和成熟，大致可以划分为政策[10-12]、区域[13]和行业[14-16]3个层面. 但是，关于大气污染物之间的协同减排研究尚不充足，且对象主要集中在SO2、NOx和PM2.5这3种污染物上，随着PM2.5与O3成为影响我国城市和区域空气质量的主要空气污染物，二者协同控制研究也开始得到学者的广泛关注，但内容主要侧重于评估不同减排情景或政策措施的实施效果，而对同时实现PM2.5和O3空气质量目标的减排路径选择的研究较少，尤其是考虑大气污染物与PM2.5、O3之间转换关系的协同减排路径研究也较为鲜见.

大气污染防控政策的实施势必会产生一定的经济成本，而一般利用边际减排成本(即每削减单位污染物所增加的经济成本)[17]来反映，如何评估污染物的边际减排成本也是学者们重点关注的问题，其评估方法大致可以分为基于减排技术和基于模型的方法[18-19]. 评估污染物减排成本的最终目的是确定成本最优的大气污染防治方案[20-23]. 国际社会应用较为广泛的大气污染防控成本优化模型为温室气体和空气污染协同作用模型(GAINS)、亚太地区综合模型(AIM/Enduse)和控制策略工具(CoST). 但是这些模型并不适合对中国城市区域污染物协同减排的研究，如GAINS模型，虽然其覆盖的污染物种类较多，但是无法解决污染物与其前体物存在响应关系的问题. 为解决该问题，Xing等[24]将美国环境保护局开发的空气污染控制成本效益与达标评估系统(ABaCAS)应用到中国的大气污染防治综合决策中，构建了一套较为完整的科学决策系统，且其费效达标的路径优化模块已十分完整，但是该系统仍有局限性，如其计算的减排成本只考虑了技术端的成本而未纳入其他社会经济成本.

由于环境税能够将环境污染和生态破坏的社会成本内化到生产成本和市场价格中，然后再通过市场机制重新分配环境资源，Bovenberg等[25]认为环境税应等同于边际减排成本. 可计算一般均衡模型(CGE)能够将环境和经济系统联系起来[26]，衡量整个经济系统受到的影响，而且可以描述整个经济系统中各部门和核算账户之间的关系，因此能较为准确地衡量减排政策产生的经济成本，笔者利用引入环境税的CGE模型来评估污染物的减排成本.

目前，关于京津冀地区PM2.5和O3协同控制的研究多数集中于政策层面的建议，而对于具体的PM2.5和O3的协同控制路径研究较少，且从PM2.5和O3二次组分来源角度分析京津冀地区PM2.5和O3协同控制路径的研究更少. 因此，该研究拟通过协同控制PM2.5和O3中的二次组分来达到空气质量目标的期望值，即在给定PM2.5和O3预期浓度目标下，给出满足目标的NOx和VOCs的排放策略，以期为京津冀地区PM2.5和O3协同控制方案提供成本有效的路径选择.

1 研究方法

1.1 京津冀城市CGE模型

该研究拟构建涵盖环境税的城市尺度京津冀CGE模型来评估NOx和VOCs的边际减排成本. 该研究构建的CGE模型的结构框架如图1所示，该框架描述了商品中间投入、居民储蓄、企业储蓄、政府转移支付等社会要素在整个经济系统中的流动关系，可用于评估某个社会要素变动对其他要素的影响. 其基本思想为实现供求关系的全局均衡，即保证生产者的供给和消费者的需求均衡. 具体包括消费者的收支均衡、生产者的供给需求均衡等. 生产者主要指国民经济中的生产部门，消费者主要包括居民、政府和企业. 限于篇幅，重点介绍生产模块和排放模块，其中排放模块的污染物主要基于图1中生产者用于生产过程以及消费者用于满足需求的能源消耗.

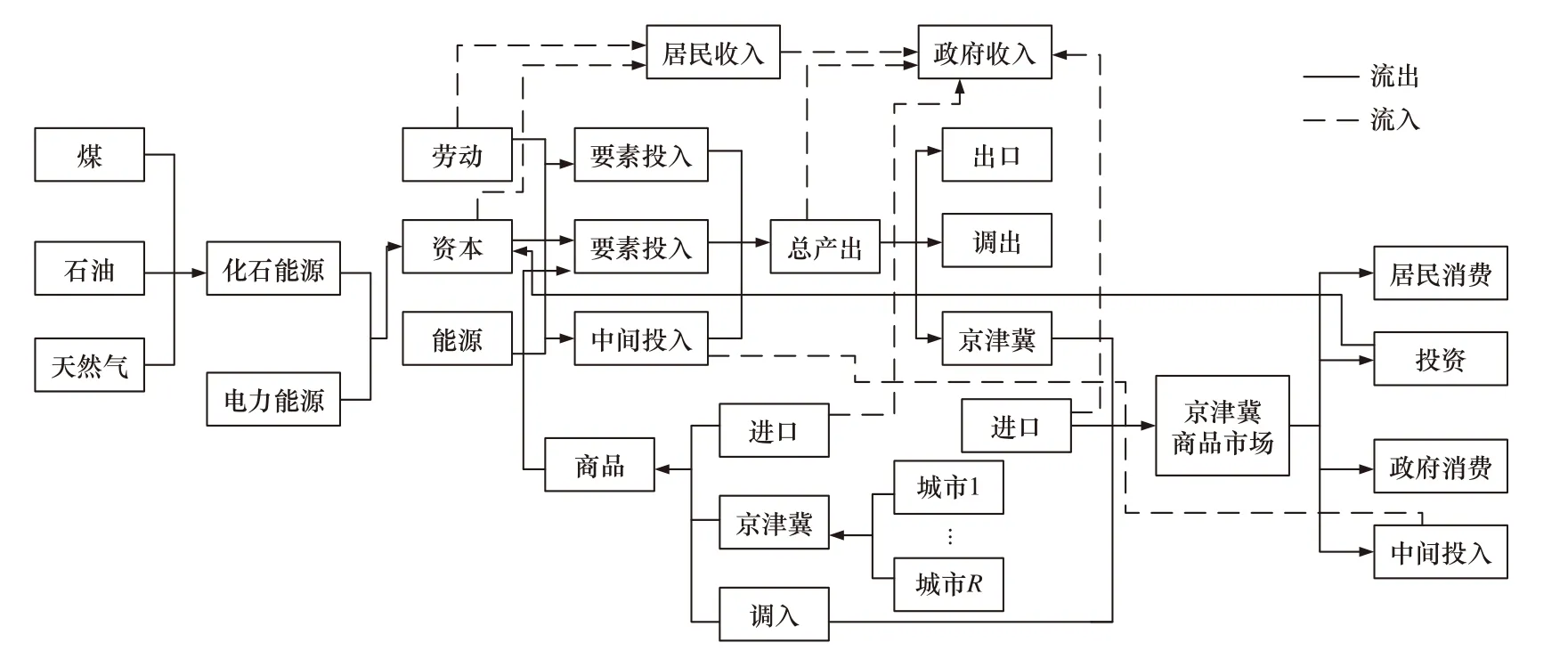
图 1 构建的CGE模型结构框架Fig.1 The structure diagram of CGE model

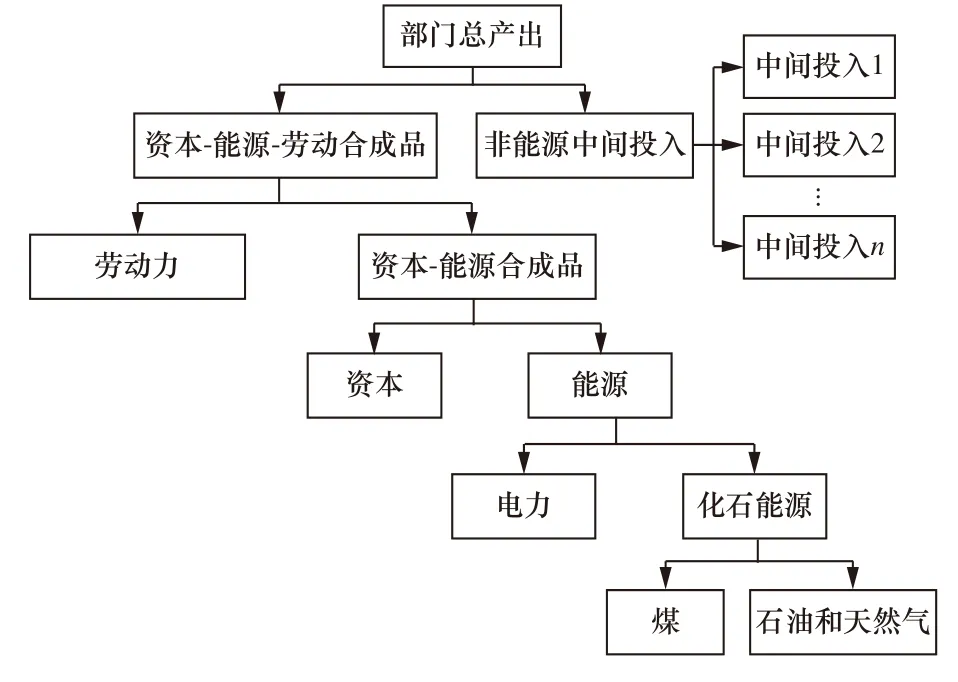
图 2 CGE模型中的生产模块嵌套结构Fig.2 The nesting structures of production module in CGE model

1.1.1生产模块

生产模块的嵌套结构如图2所示，共包含5层嵌套关系. 第一层的部门总产出由资本-能源-劳动合成品与非能源中间投入采用列昂惕夫函数(Leontief)合成；第二层的非能源中间投入之间的替代关系利用Leontief描述，同时资本-能源-劳动合成品由劳动力与资本-能源合成品采用恒替代弹性生产函数(CES)进行合成；第三层的资本-能源合成品由资本和能源采用CES函数进行合成；在第四层嵌套中将能源划分为电力和化石能源；第五层生产部门消耗的化石能源主要包含煤炭、石油和天然气，由于基础数据中将石油和天然气的行业数据进行了合并，故生产函数中表示为“石油和天然气”一种能源，其与煤炭能源的替代关系采用CES函数形式进行描述.

1.1.2排放模块

污染物的排放来自能源的使用，而生产、生活和投资等活动都会涉及能源的消耗，因此污染物的总排放量为生产消费活动的能源消耗量与相应污染物排放系数的乘积. 由于能源的消耗包括工业生产、能源投资、居民和政府消费四部分，故NOx和VOCs的来源主要为上述四部分. 四部分的能源消耗数据主要来源于投入产出表，鉴于数据的可获得性，假定四部分的污染物排放系数是一样的. 由于过程排放也是VOCs的重要来源，如工业生产过程中溶剂的使用也会产生VOCs的排放，故度量VOCs的排放量时需要考虑VOCs的过程排放.

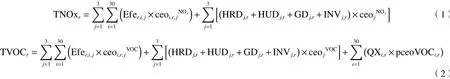
式中：T NOxr、 TVOCr分 别为区域r中NOx、VOCs的排放量，t； Efer,i,j表示区域r行业i对化石能源j的消耗量，108元； ceoi,r,jNOx和 ceoi,r,jVOC分别为区域r行业i中化石能源j的NOx和VOCs排放系数，t/(108元)；H RDj,r、HUDj,r分别为区域r中农村、城镇居民对能源j的消耗量，108元； GDj,r为 政府对能源j的消耗量，108元；INVj,r为能源投资量，108元； Q Xi,r为工业产出，108元；pceoVOCi,r为过程排放系数，t/(108元).

区域r中能源j中间投入部分征收的环境税税额(T AXr,j)的计算公式如式(3)所示. 计算出化石能源的环境税税额后，可将环境税的税率(ttcr)转化为从价税率(t cvr,j)，即对某种化石能源征收的环境税税收与该化石能源的国内需求的价值量之比〔见式(4)〕.通过设置不同的环境税率求解相应的减排比例，从而得到污染物的边际减排成本. 由于污染物的边际减排成本函数常用二次曲线形式〔见式(5)〕[27]，故利用二次型函数形式对污染物的边际减排成本函数进行评估，参数从基于Matlab程序拟合得到的边际减排成本曲线中获得.

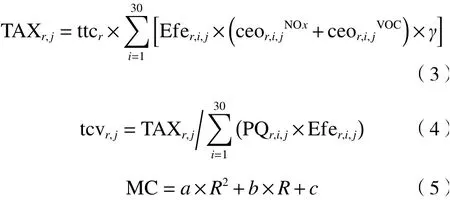
式中：γ表示将碳税收入单位与模型中价值型变量单位进行统一的系数；PQ表示能源商品的价格，108元；MC 表 示用CGE模型得到的边际减排成本，元/t；R表示污染物的减排比例，%；a、b与c均表示边际减排成本曲线拟合得到的参数.

1.2 京津冀PM2.5和O3协同控制评估模型

为制定考虑成本的减排策略，构建了PM2.5和O3协同控制评估模型〔见式(6)~(11)〕. 整体上，该模型为非线性优化模型，空气质量目标为约束条件，最小减排成本为目标函数. 此外，由于区域间还存在污染物的传输效应[28]，故也将区域间的传输关系考虑在区域最终空气质量的测算过程中，以保证所制定的模型更加贴近大气污染来源的现实状况.

式中：T Cost 表示污染物减排总成本，108元；n为 区域r的总个数；p为污染物的种类数； Costrp表示污染物p(NOx和VOCs)在区域r的减排成本，108元. 区域r中O3浓度和PM2.5浓度对污染物p排放比例的响应关系如式(7)(8)所示，其中，函数和RSMPM2.5为非线性响应关系函数〔见式(12)〕；表示达到空气质量目标时的O3浓度，表示达到空气质量目标时的PM2.5浓度，表示NOx的减排量小于基准排放量，单位均为t；表示VOCs的减排量小于基准排放量，单位均为t. 当考虑区域传输时，京津冀地区各城市PM2.5和O3的最终浓度可用传输矩阵(An×n，Bn×n)与污染物初始浓度的乘积表示. 该研究用到的污染物非线性响应关系基于CMAQ模型模拟得到[29].

由于污染物减排与空气质量的改善在很多情况下呈现非线性的复杂关系，其对于污染控制决策的制定带来很大的困难，因此为达到协同控制PM2.5和O3的目的，最为关键的是量化PM2.5和O3与其共同前体物(NOx和VOCs)的非线性响应关系. 非线性响应关系函数的基本框架有以下几点：①根据决策需求确定关键的控制因子，选取NOx和VOCs作为PM2.5和O3的控制因子；②借助采样方法设计一系列排放情景；③确定试验参数，即控制因子数、采样方法及采样数；④对每种情景通过CMAQ模型模拟得到的结果进行非线性归纳来获取响应关系. 基于此，参考文献[30]利用多项式函数对该非线性响应关系进行显性表达〔见式(12)〕.

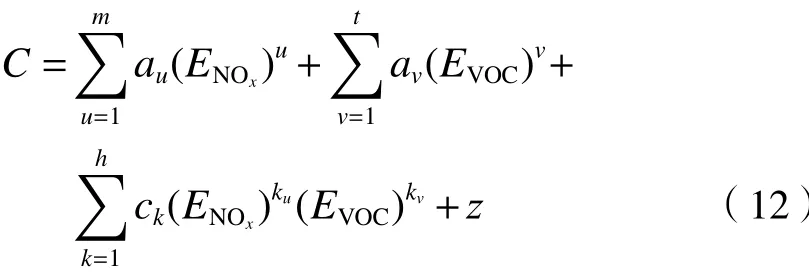
式中：C表示PM2.5和O3对其前体物排放量变化的响应浓度，μg/m3；ENOx、EVOC分别为NOx和VOCs的排放比例，%；au、av和ck分别表示NOx、VOCs和两污染物组合的排放系数；m和t分别为NOx和VOCs排放比例的最高阶数；u和v分别为NOx和VOCs不同非线性程度的拟合阶数；h为两种前体物相互作用的总次数；ku和kv表示两种前体物(NOx和VOCs)不同线性程度的相互作用关系；z为多项式拟合过程中的常数项.

2 结果与讨论

2.1 京津冀地区NOx和VOCs的边际减排成本

利用京津冀城市尺度CGE模型评估NOx和VOCs的边际减排成本，可得到不同减排比例对应的边际减排成本，进而利用回归分析的方法得到NOx和VOCs的边际减排成本函数以及对应的边际减排成本曲线，其拟合效果较好，拟合优度均高于0.95. 由于京津冀地区城市较多，考虑到结果的可视性，该研究只展示几个代表城市的NOx和VOCs的边际减排成本曲线(见图3).

图 3 京津冀地区部分城市NOx和VOCs的边际减排成本曲线Fig.3 The marginal abatement cost curves of NOx and VOCs in some cities of Beijing-Tianjin-Hebei Region

由图3可见：随着减排比例的提高，各城市NOx和VOCs的边际减排成本均不断上升，且边际减排成本的上升速度高于减排比例，即边际减排成本函数为凹函数. 此外，在相同减排比例下，NOx的边际减排成本低于VOCs. 当减排率为50%时，各城市NOx的边际减排成本不超过515元/污染当量，且主要集中在90~150元/污染当量范围内；各城市VOCs的边际减排成本最高值超过750元/污染当量，大部分城市的VOCs边际减排成本在200~300元/污染当量之间. 比较各城市的边际减排成本可以发现：北京市NOx和VOCs的边际减排成本相对较高，且升幅最快，这与北京市的经济发展状况和减排现状相符，北京市各部门的经济运行联系较为紧密，一个部门的生产出现变化(如减少化石能源的投入)，整个经济系统就会受到较大的影响；天津市和河北省各城市的边际减排成本较低且差距较小，随着减排比例的上升，成本差距逐渐增大. 若通过减排成本来评估减排潜力，则张家口市NOx和VOCs的减排潜力最大，因为相同减排比例下其边际减排成本最低.

通过对比已有研究[31-32]发现，利用自下而上和自上而下的方法构造出的污染物边际减排成本曲线多为二次凹函数形式，即与笔者构建的边际减排成本曲线形式相同. 为方便与其他研究成果进行比较，将笔者研究中边际减排成本的单位(元/污染当量)换算为元/t. 秦昌波等[33]利用GREAT-E模型评估发现，当NOx总排放量减少1.7%时，NOx的税率为5 040元/t，而笔者研究中相应NOx减排率下京津冀地区平均税率约为5 991元/t. 刘昌新等[34]指出，当VOCs的减排量为5.05%时，间接税税率为50%，按照其计算税额的方法，可计算出VOCs的税率约18.8×104元/t，而笔者发现，当VOCs减排量为5.05%时对应的京津冀地区VOCs平均税率为12.6×104元/t. 笔者研究结果与已有研究出现偏差的原因可能有以下三点：①各研究的基准年份不同，不同的基准方案的设置会对结果产生一定的偏差；②各研究关于替代参数的设置等基本假设可能存在偏差；③直接税和间接税的税率值不同，所以导致VOCs的税率存在差距. 孙新丽等[35]利用大气污染防治综合决策支持技术平台评估得到，当NOx总排放量减少20%时，NOx的税率为3 000元/t左右，VOCs的税率为5 000元/t左右，而笔者研究中相应减排率下京津冀地区NOx和VOCs平均税率分别为3.5×104和6.8×104元/t. 成本差距较大的原因在于孙新丽等[35]研究中以济南市《2018年大气污染治理“十大措施”实施方案》实施后的PM2.5浓度为总体减排目标，降幅仅为19%，且以60 μg/m3为PM2.5预期达到的设定标准，减排幅度远低于笔者研究设定的减排目标(35 μg/m3)下污染物的减排幅度，故减排成本相对较低. 虽然，笔者研究与已有研究结果存在差距，但差值在可接受范围内，故笔者研究中构造的边际减排成本曲线是可行的.

2.2 京津冀地区PM2.5和O3协同控制方案

中国计划在2035年实现各城市空气质量达到《国家环境空气质量标准》(GB 3095−2012)二级标准限值，即PM2.5浓度不超过35 μg/m3，O3浓度不超过160 μg/m3. 因此，以实现京津冀地区PM2.5和O3浓度协同达到GB 3095−2012二级标准为目标，利用上述PM2.5和O3协同控制评估模型，确定经济成本最小化下京津冀地区NOx和VOCs的具体减排方案.基准年份为2017年，将基准年份的排放数据以及其他基础数据代入PM2.5和O3协同控制评估模型，进而测算出京津冀地区各城市NOx和VOCs所需的减排比例，且在该减排比例下减排成本最小(见图4).

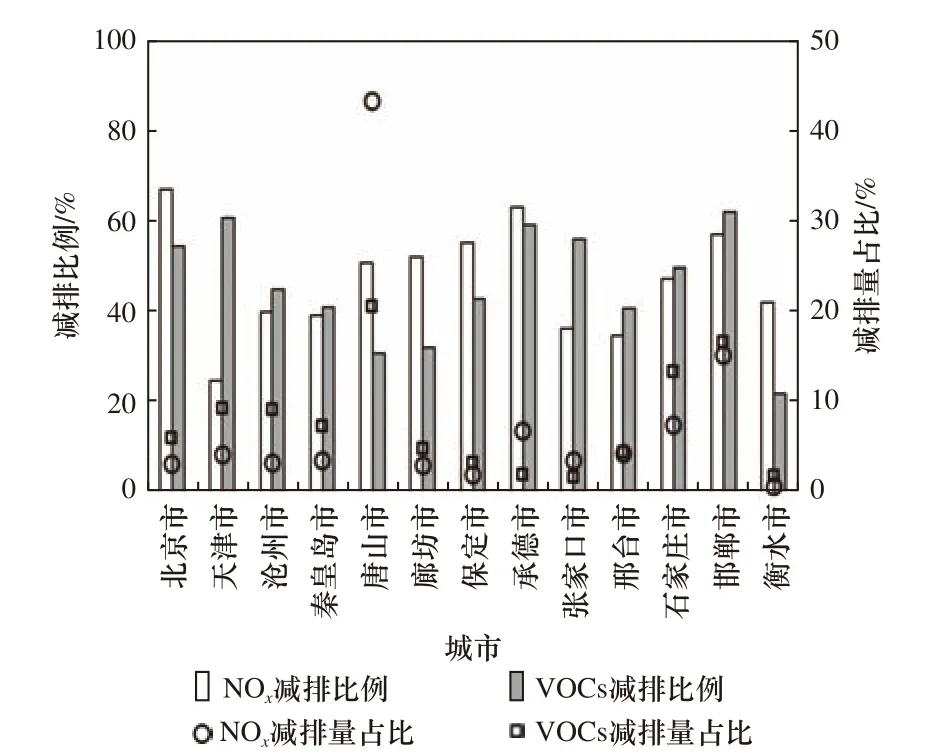
图 4 京津冀地区协同减排方案Fig.4 The collaborative reduction strategy in Beijing-Tianjin-Hebei Region

由图4可见，为实现京津冀地区PM2.5和O3协同达标，相较于2017年，京津冀各城市需要减少NOx和VOCs的排放比例分别为25%~67%和22%~60%.从污染物减排力度来看，京津冀地区13个城市中，NOx减排比例超过60%的城市为北京市和承德市，VOCs减排比例超过60%的城市为天津市和邯郸市，NOx减排比例为40%~60%的城市包含6个，VOCs减排比例为40%~60%的城市包含8个. 从污染物类别来看，各城市NOx和VOCs减排比例差距较小，但是超过半数城市的VOCs减排比例高于NOx，特别是天津市的VOCs和NOx减排比例差值高于30%. 从区域的角度来看：北京市NOx和VOCs的减排比例均超过50%，与Xing等[24]研究中北京市实现PM2.5和O3同时达标时NOx和VOCs减排比例均高于50%的结果一致，且与河北省承德市的减排比例较为接近；天津市的VOCs减排比例居于第二位，而其NOx的减排比例处于末位；对于河北省来说，将河北省的城市分东部(沧州市、秦皇岛市、唐山市、廊坊市和保定市)、北部(承德市和张家口市)和南部(邢台市、石家庄市、邯郸市和衡水市)3个区域，相较于南部和北部区域城市，东部区域城市NOx和VOCs的减排比例较小.

此外，为衡量各城市在协同减排任务中的责任，计算了各城市的减排量占比(即某城市污染物的减排量与该污染物在京津冀地区总减排量的比值). 可以发现，由于唐山市、石家庄市和邯郸市NOx和VOCs的排放量基数较大，故其减排量居于前三位，尤其是唐山市，其NOx和VOCs的减排量占比均接近45%，邯郸市NOx和VOCs的减排量占比分别为15.2%和16.6%. 对于北京市和天津市，NOx的减排量占比较为接近，分别为3.1%和4.2%，VOCs的减排量占比存在差距，分别为5.9%和9.2%，但是与唐山市和邯郸市相比，减排量占比较低. 总的来说，相较于北京市和天津市，河北省对于京津冀地区协同减排的责任更大.

基于边际减排成本曲线，评估了京津冀各城市PM2.5和O3达标时需要的总减排成本，北京市为177.5×108元，天津市为83.6×108元，河北省为731.8×108元，京津冀地区总减排成本为992.9×108元. 邢佳等[30]研究表明，当2035年PM2.5浓度达标时，北京市NOx和VOCs的总减排成本在160×108元左右，天津市NOx和VOCs的总减排成本在60×108元左右，略低于笔者研究结果. 其主要原因是笔者研究考虑了PM2.5和O3同时达标，减排目标更严格，减排成本会更高，一定程度上也验证了笔者研究结果的可靠性.多数城市的减排成本占本城市GDP的比例都不超过1%，减排成本较高的前3个城市分别为唐山市、邯郸市和北京市，减排成本均超过100×108元. 由图5可见，京津冀地区VOCs的总减排成本高于NOx的总减排成本，VOCs减排成本(超过70×108元)较高的城市为邯郸市、北京市、天津市、石家庄市，NOx减排成本较高的城市为唐山市、邯郸市、北京市.

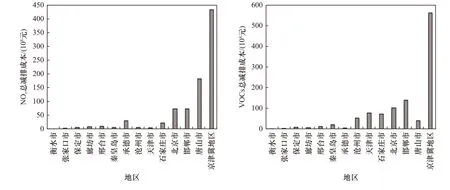
图 5 京津冀地区2017年NOx和VOCs的总减排成本Fig.5 The total abatement cost of NOx and VOCs in 2017 in Beijing-Tianjin-Hebei Region

为评估上述京津冀地区PM2.5和O3协同控制方案的实施效果，进一步预测了NOx和VOCs减排后PM2.5和O3的浓度. 由图6可见：北京市和天津市的O3浓度有较大改善，约为140 μg/m3，河北省各城市的O3浓度虽然未低于150 μg/m3，但都达到了GB 3095−2012二级标准；与O3浓度的变化状况不同，河北省北部和南部区域城市(除石家庄外)PM2.5浓度相对较低，北京市、天津市和河北省东部区域大部分城市的PM2.5浓度在30~32 μg/m3范围内，也均达到目标. 此外，减排方案实施后，唐山市和石家庄市PM2.5和O3的预测浓度均居于前列，因此与其他城市相比，这两个城市的空气质量改善任重道远.

图 6 协同减排方案实施后京津冀地区的PM2.5和O3浓度Fig.6 The concentrations of PM2.5 and O3 in Beijing-Tianjin-Hebei Region under the collaborative emission reduction strategies

2.3 稳健性检验

为了使该研究的结果更有说服力，首先对计算减排成本的CGE模型做了敏感性分析，主要对生产替代弹性参数、阿明顿替代弹性参数和CET替代弹性参数进行了敏感性分析. 该研究随机选择北京市和保定市的1个或2个部门的生产替代弹性参数、阿明顿替代弹性参数和CET替代弹性参数进行分析. 结果表明，当3个弹性参数改变±10%和±20%时，各变量的变化小于0.01%. 对模拟结果的影响较小，说明了该研究所建立模型的可靠性.

此外，考虑到不同前体物对空气质量影响等方面存在不确定性，该研究从两方面对构建的协同控制模型进行了稳健性检验. 首先，对模型采用的非线性响应关系函数的拟合程度进行了检验，发现其拟合效果较好，拟合优度均高于0.9，表明模型可以较好地反映PM2.5和O3与其共同前体物NOx和VOCs之间的响应关系，进而提高测算出的京津冀地区各城市NOx和VOCs所需的减排比例的准确性；其次，通过反算模型给出的减排量及减排方案推算出相应的PM2.5和O3浓度，并验证了二者浓度均满足达标需求，这在一定程度上印证了该研究建立的PM2.5和O3协同控制模型的可靠性.

3 结论与展望

3.1 结论

a) NOx和VOCs的边际减排成本均随着减排比例的提高而上升，且边际减排成本的上升速度高于减排比例. 相同减排比例下，NOx的边际减排成本低于VOCs. 北京市NOx和VOCs的边际减排成本明显高于天津市和河北省各城市，天津市和河北省各城市的边际减排成本差距较小，但随着减排比例的升高，差距逐渐增大.

b) 为实现京津冀地区PM2.5和O3浓度的协同达标，并保证减排成本最低，相较于2017年，京津冀地区13个城市NOx和VOCs的减排比例分别为25%~67%和22%~60%. 京津冀地区需要投入的总减排成本为992.9×108元.

c)从具体的减排路径上来看，北京市和承德市的NOx减排比例，以及天津市和邯郸市的VOCs减排比例居于前两位，河北省各城市的污染物减排量远高于北京市和天津市，特别是唐山市、石家庄市和邯郸市，此外河北省东部城市的减排压力低于北部和南部区域城市.

3.2 展望

a)该研究结果的政策启示体现在以下几方面：①该研究发现，北京市、天津市和河北省的边际减排成本逐步递增，为我国当前环境保护税实施的差异化税率提供了支撑. 中国自2018年实施的《中华人民共和国环境保护税法》规定大气污染物的税率为1.2~12元/污染当量，如北京市实施的是最高上限税率. 建议京津冀地区在其他类型大气污染协同减排策略设计过程中也能进一步体现地区之间的差异性. ②该研究在减排成本最小化目标下，设计了京津冀地区PM2.5和O3浓度达到GB 3095−2012二级标准时各地区NOx和VOCs的协同减排方案，研究结果可以为京津冀地区减排目标的分解提供参考. 此外，河北省唐山市、石家庄市和邯郸市是实现京津冀地区空气质量改善的关键，承担的减排损失也相对较大，然而目前我国空气质量补偿机制仍局限在各省份内部，建议建立京津冀地区跨区域横向空气质量补偿机制，助力京津冀地区大气污染协同治理. ③该研究构建的京津冀城市CGE模型以及PM2.5和O3协同控制评估模型丰富了京津冀地区大气污染治理的分析工具，为京津冀地区城市层面环境政策模拟仿真提供了新的平台.

b)该研究构建的模型可以在未来进一步改进：①污染物之间的响应关系只考虑了PM2.5和O3与其共同前体物之间的关系，但是其他一次污染物也分别会对PM2.5和O3产生作用，因此可以扩充污染物响应关系的因子库. ②PM2.5和O3之间也存在相互影响，研究两污染物之间的影响机制对于二者协同减排也十分重要. ③深化协同减排的研究层面，目前研究主要侧重于区域间污染物的协同减排，未来的研究可以深化到各区域行业层面的污染物协同减排. ④污染物减排成本不仅包含对企业造成的成本，还包括对宏观经济造成的影响，如何耦合经济成本和减排技术成本，也是一个值得关注的问题.