基于支持向量机的飞机颠簸预测方法研究
李朝潞,吴俊杰,万连成
(中国民用航空飞行学院 空中交通管理院,四川 广汉 618300)
0 引言
实践和研究表明,多变地形对飞机近地面飞行的安全影响极大[1],飞机颠簸是其表现形式之一。与地形有关的飞机颠簸主要是由风吹过多变地形形成的动力湍流引起的,大多发生在飞机起飞和下降过程,且在飞行高度较低区域。
飞机颠簸是指在飞行中飞机突然出现的忽上忽下、左右摇晃及机身振颤的现象。大气湍流是造成飞机颠簸的主要原因,可分为动力湍流、热力湍流、晴空湍流、尾涡湍流和山地波等[2]。其中,引起飞机低空颠簸的大气湍流主要为动力湍流和热力湍流[3-4]。
由于低空颠簸多发且复杂,为对其进行准确预测,基于实测数据进行准确的定量分析就显得尤为重要。飞机在低空飞行时,尤其是在起飞和降落阶段,地形条件的影响尤为严重[5]。风吹过多变地形会产生风切变,风切变在近地飞行区发生时,飞机会突然不受控制上升或下降[6]。此时,飞机距地面较近,调整空间有限,是飞机起降的危险阶段。
在地形多变的山区,动力因子和热力因子会相互影响形成不同类型湍流,其程度与山脉的形状和大小有关。山地波是气流流经山地时,随山地高度分布不均匀产生的,能产生上升和下沉气流速度很大的湍流[7-8]。飞机在该区域,经常会产生强颠簸。由于山区动力因子和热力因子的共同作用,常见湍流形式有山谷环流、山地湍流和山地波。此外,地形和分层气流的相互作用会在山脉背风面形成各种尺度的湍流涡旋,产生重力波和背风转子环流等,严重影响飞行安全[9]。这些都与水平风的垂直变化有关,可见,低空飞行时飞机颠簸主要源自水平风的切变[10]。
虽有少量基于实测资料对多变地形上空飞机颠簸的研究,但结合实际飞行航线,考虑机场附近多变地形并引入地形物理参数的相关研究鲜有报道。本文以开普福尔德地区为研究对象(该地风向稳定且飞机颠簸受山顶影响较为明显),使用5种与地形有关的物理量参数,通过支持向量机算法,探求近地面飞机颠簸区的预测方法。
1 数据预处理
飞机颠簸数据来源于美国国家航洋和大气管理局的AMDAR飞机数据。大气数据选用欧洲中期天气预报中心的再分析数据资料。其数据原始格式为经纬度每0.125°×0.125°一个采集点,每24小时采集4次。根据飞机颠簸高度选择合适气压高度的水平风速、垂直风速与温度数据。将下载后的nc格式数据文件用MATLAB中的netcdf函数库进行处理,使用ncdisp和ncread指令可以对nc文件的数据信息进行查看和读取。地形数据取自地理信息云提供的免费DEM数据,使用ArcGIS对其进行解码,将开普福尔德上空航线附近的地形数据按照0.25°×0.25°的范围分成18个栅格,并求出每个栅格中的地形局部高差与最高高度。地形起伏度可根据DEM数据使用ArcGIS中的插值函数计算得出,其算法原理为局部高差算法,计算公式为
ra=emax-emin
(1)
式中:ra为地形起伏度;emax和emin分别为每个栅格范围内的最大和最小高程,结果如图1所示。
地形最高高度同样可以在ArcGIS中生成,结果如图2所示。
图1和图2中栅格的颜色越浅,表示其对应的数值越大。排除飞行航线不经过的栅格,留下航线两旁的18个栅格作为研究对象。
2 支持向量机算法
聚类分析是数据分析的主要方式。可以用来计算数据空间上的密集区域、间隔或分成不同类别,可将其视为多目标规划问题。目前已有超过100种聚类算法,这些算法由于所用数据集的特点不同,应用的范围也不同。统计学习理论专门研究实际应用中有限样本情况的机器学习规律,并发展了支持向量机(Support Vector Machine, SVM)算法,该算法基于结构风险最小化(SRM)原理,具有很多优于已有方法的性能[11]。
设样本为(x1,y1),(x2,y2),…,(xn,yn),最优化函数为f(xi,w),在统计学中,利用风险最小化准则的经验风险为
(2)
式中,L为拉格朗日函数。将实际风险代入经验风险中,经验风险与实际风险之间满足如下关系
(3)
式中,n是样本数,函数h表示了函数的复杂性[12]。从式(3)可以看出,函数的复杂性与真实风险和经验风险之间的差别成正比。当两者的差别较大时,证明机器学习的过程出现了过学习的现象,因此在机器学习过程中要控制上述两者间的差值才能得到较好的预测结果[13-14]。
SVM的最初只能用于将数据集合分为两类,即用可描述的线段将数据分割成两个类别,如图3所示。图中上面和下面的点表示两类样本,直线为判别函数(区分多类问题可将直线描绘为一个超平面),该直线将机器训练集合分割为正负两类。
按照经验风险最小化的要求,图3中的直线(超平面)对数据的分类效果良好,若更换训练样本数据集,其效果将显著降低,难以将其推广到其他数据集上进行其他模式的数据预测。按照结构风险最小化的要求,图3中的直线(超平面)应在将两种数据集分开的同时实现分类间隔最大。SVM可将这种预测推广到其他的问题中去。
SVM最大分类间隔是在两类未被分类的数据之间找到临界函数,将这两种数据分割开来。但这种临界函数存在无数个,SVM找到其中最优的,并将其作为这个分类问题的最优解。此时,最优的分类间隔为最大分类间隔。假设一个n维超平面方程为:
w·x+b=0w∈Rn,b∈R
(4)
最优超平面可通过求解‖w‖2/2的极小值得到。对其增加约束条件:
yi(w·xi+b)-1≥0i=1,…,n
(5)
该约束优化问题可用拉格朗日方法求解,其函数表达式如下:
(6)
式中,αi为第i个样本的拉氏因子(αi≥0)。由式(6)分别对w和b求导,并令所得导数方程等于0,有
(7)
(8)
选择超平面时,拉氏因子为0的样本向量对选择分类超平面没有意义,可选解向量的拉氏因子均不为0。这样,从训练集中就可得到描述最优分类超平面的决策函数(支持向量机),其分类功能由支持向量决定。决策函数表达式为:
(9)
在线性不可分的情况下,如果存在没有被分类的数据,可在式中增加一个松弛项ξi(ξi≥0),则
yi(w·xi+b)≥1-ξii=1,2,…,n
(10)
则目标函数可改为求下式最小值
(11)
由决策函数式(9)可知,(x·xi)为x和xi的相似度。在一般情况下,对任意两个样本向量x和xi,都存在核函数来描述两者的相似度。对于难以线性分类的问题,待分类样本可通过非线性变换映射到高维特征空间,使待分类样本在目标高维空间转化为线性可分问题。若非线性转换函数为Φ(x),则超平面决策函数式可表达为:
(12)
实际中经常遇到的是线性不可分问题。核函数先将样本数据在低维空间进行运算,再将运算后的结果转换到高维空间,实现问题从低维到高维转换,且可避免运算效率低的问题。但核函数种类较多,在一种核函数下观察到的特征不一定能在其他核函数下保持。因此,选择合适的核函数解决具体问题非常重要。
3 支持向量机最优核函数的确定
为分析开普福尔德地区多变地形对飞机颠簸的影响,本文采用常见的四种核函数[15]进行分析,其中一个为线性核函数,三个为非线性核函数。
线性核函数表达式如下:
K1(x·xi)=x·xi
(13)
非线性核函数有如下三种:
(1)多项式核函数的表达式为:
Kp(x·xi)=[(x·xi)+1]q
(14)
式中,q表示多项式阶数为q阶。
(2)径向基核函数的表示式为:
(15)
(3)Sigmoid核函数的表示式为:
Ks(x·xi)=tanh[υ(x·xi)+c]
(16)
基于上述4种不同核函数建立SVM模型,根据4种模型的预测结果,选择其中结果最好的为最优核函数。
将开普福尔德地区航线附近区域划分为18个栅格,整理每个栅格中2019年一整年的相关数据,包括栅格上空气象数据、栅格内地形起伏度以及每天发生飞机颠簸的次数,将上述数据作为训练集代入四种SVM模型中。为评价航线附近栅格中飞机的颠簸等级,统计每个栅格中飞机日颠簸次数,并按照统计结果划分为不同的等级。日颠簸次数小于1次的为非颠簸区,记为0;日颠簸次数大于等于1次小于3次的为中度颠簸区,记为1;日颠簸次数大于等于3次的为重度颠簸区,记为2。SVM模型训练集中的部分统计数据如表1所示。
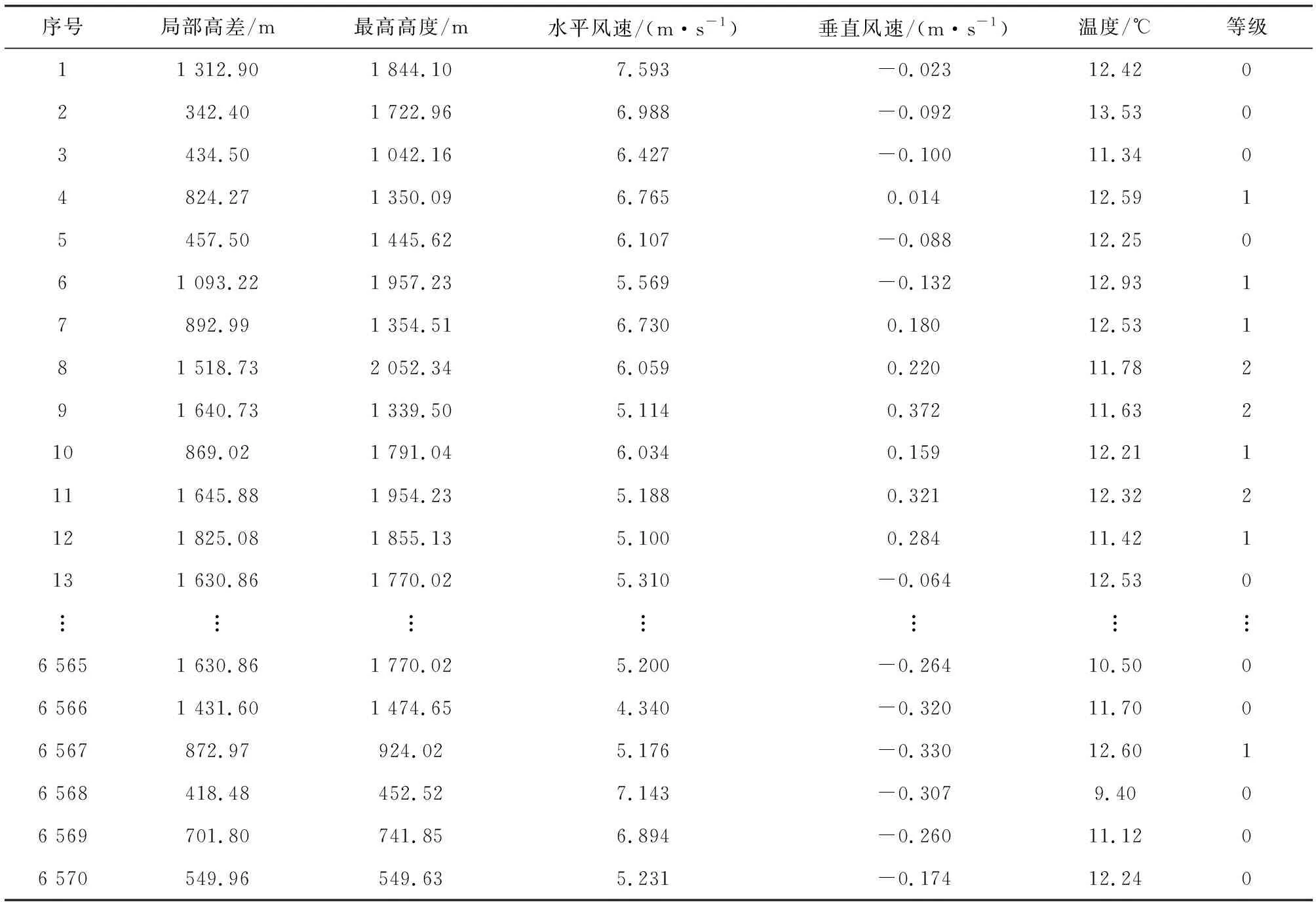
表1 SVM模型训练集中的部分统计数据
使用Python将整理好的训练集数据分别代入四种不同核函数的支持向量机对飞机颠簸进行预测结果,如图4所示。图中linear为线性核函数预测结果,poly、rbf、sigmoid分别为多项式、径向基、Sigmoid核函数预测结果,real为实际结果。
由图4可知,线性核函数、多项式核函数、径向基核函数和Sigmoid核函数四种核函数预测正确率分别为61.0%、83.3%、61.0%和44.4%。显然,多项式核函数的预测效果最好。将不同的地形参数组合分别代入训练集,使用多项式核函数的支持向量机求出预测结果,并确定最优的参数组合。
4 最优地形参数组合的确定
为了验证所选择的与地形相关的参数是否全部与飞机颠簸在栅格上空发生次数相关,再次建立SVM模型,带入不同的参数组合,并对飞机颠簸次数进行预测。表2为测试集所对应的参数组合。

表2 15种参数组合
图5中可以看出预测准确率最高的参数组合的序号为3,预测准确率为94.44%。其中,序号为3的模型所选取的参数为局部高差、最高高度、水平风速、垂直风速。序号为2与4的模型预测效果也较高,其余模型测试结果不太理想。因此可以推测栅格上空的飞机颠簸发生次数主要与地形的局部高差、地形最高高度、水平风速、垂直风速相关。
5 结论
本文分别建立4种不同核函数下的支持向量机模型。对比4种核函数的预测结果得出结论,多项式核函数对上述5种参数的预测效果最佳。找出5种与地形相关参数的不同参数组合的情况并列出表格,将15种不同参数组合分别代入多项式核函数下的支持向量机对飞机颠簸强度进行预测,预测结果表明地形局部高差、最高高度、水平风速与垂直速度的参数组合的预测准确最高,即得出结论,这4种参数与飞机在地形上空发生颠簸的关系最大。

