沉管隧道底板减重方案下结构受力分析

黄鹏志

（广州市市政工程设计研究总院有限公司 广州 510060）

0 引言

城市的发展离不开交通建设，面对横穿城市的江河，过江通道成为了连接江河两岸交通的重要基础设施。但过多地采用桥梁的形式显然会对两岸江景、内河航运、岸边土地利用造成不利影响，因此，水下隧道愈来愈广泛地被用于城市复杂环境的过江通道建设中［1-5］。在众多水下隧道形式中，沉管隧道由于具有埋深浅、两岸接线短的特点［6-8］，成为了城市过江水下隧道的首选形式。

沉管隧道的建设若采用独立干坞方案，首先需要在干坞中预制隧道管节［9-10］，后将管节通过浮运航道浮运至设计隧址区进行沉放对接［11］。而在沉管浮运过程中，管节浮于水中需满足一定的干舷高度，且保证管节底板与河床底之间留有安全距离［12］，因此在城市内河河道较浅的区段，必须对河床进行开挖疏浚。若沉管自重过大，则在浮运过程中吃水较深，浮运航道河底的清淤疏浚工程量也较大［13］。因此，对沉管隧道管节进行减重，可降低管节在水中的吃水深度，提高管节在浮运过程中的通过性，同时可减少浮运航道的疏浚开挖量，节约成本。本文通过改变沉管隧道管节底板的截面形式，减少底板混凝土的体积，达到管节减重的目的，并使用有限元模拟软件对减重方案中沉管结构受力进行了计算分析，同时将其与传统截面形式沉管结构受力作对比。

1 沉管底板减重方案概况

沉管隧道管节总长101 m，横断面如图1 所示，管节宽29.6 m，高9.2 m，顶底板厚度为1.25 m，侧墙厚度为1.0 m，管节整体截面面积为272.23 m2，实体结构截面积为99.85 m2，每节沉管混凝土总重25 500 t。

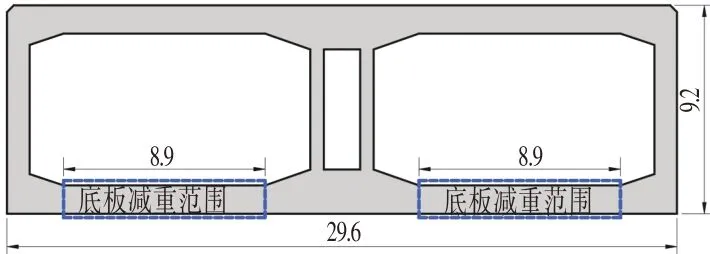
图1 沉管隧道横断面示意图Fig.1 Schematic of Cross Section of Immersed Tunnel （m）

为减少沉管隧道底板混凝土用量，将沉管下部左右两撇脚间的底板截面由原有的1.25 m 厚的矩形板状形式转换为翼缘相连的连续倒置T 形梁，如图2所示，相当于在底板左右两撇脚之间每隔1.0 m 挖除一块8.9 m×2.0 m×0.5 m（长×宽×高）的混凝土，并将所形成的凹槽之间的梁加高0.5 m 作为倒T 梁的腹板。经截面转换后，每节沉管管节可减少702.96 t混凝土，提升干舷高度0.25 m。

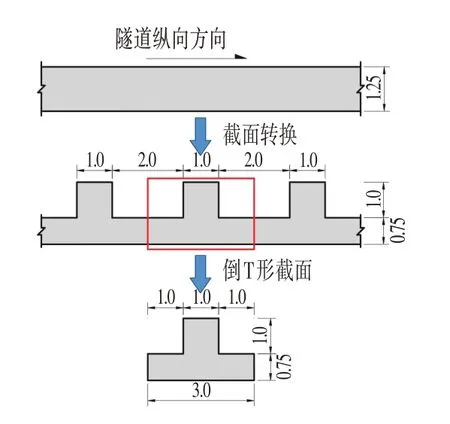
图2 底板截面转换示意图Fig.2 Schematic of Bottom Plate Section Conversion（m）

2 沉管隧道截面有限元模型建立

2.1 几何模型的建立

采用MIDAS Civil 有限元结构计算软件进行模拟计算，在软件中建立了截面转换前后的沉管隧道结构二维模型，如图3所示。模型尺寸与实际尺寸相同，为29.6 m×9.2 m（长×宽）。

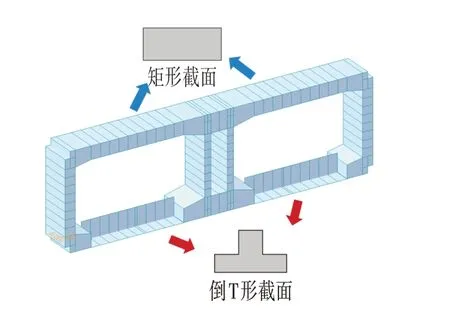
图3 沉管隧道结构模型Fig.3 Immersed Tunnel Structural Model

模型采用二维梁单元模拟隧道结构，其中，传统沉管隧道结构中的梁单元为矩形截面梁，而在减重方案模型中隧道底板减重部分的梁单元被替换为倒T 形截面梁。模型中底板原矩形截面梁梁高1.25 m，转换后的倒T 形梁梁高1.75 m，翼缘厚度0.75 m，翼缘宽度1.0 m，腹板宽度1.0 m。为了使两者计算结果可直观进行对比，原矩形截面梁与转换后的倒T 梁的梁宽均为3.0 m。

2.2 材料参数的确定

沉管隧道管节采用C40混凝土，其容重γ=25.0 kN/m3，弹性模量E=3.25×107kPa，泊松比为0.2。由于内河沉管隧道一般采用换填式复合基床，根据工程经验，本次模拟的地基弹性系数取5.0×103kN/m3。

2.3 荷载计算

本次模拟采用荷载-结构法，沉管隧道结构承受的荷载主要考虑有结构自重，顶板处的水压力、回填土压力，侧墙处的水压力、侧向土压力，底板处的浮力、地基反力，其荷载如图4 所示。由于减重后的倒T 形梁截面宽为3.0 m，因此作用于模型上的荷载应为隧道纵向3.0 m内荷载之和，即每延米荷载的3倍。

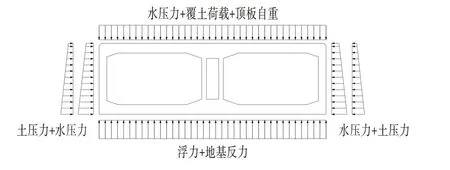
图4 沉管隧道横断面荷载Fig.4 Cross-section Load of Immersed Tunnel

荷载计算如下：

⑴顶板处每延米水压力：计算断面顶板上表面标高取-4.97 m，水位按+7.79 m的百年一遇水位计算，重力加速度g=9.8 m/s2，水的密度ρ=1.0×103kg/m3，则顶板每延米水压力为P=ρgh=0.125 MPa。

⑵顶板每延米土压力：顶板覆土高度h=5.66 m，覆土有效重度γ=7.6 kN/m3，因此顶板上表面土压力为q=γ h=43.02 kPa。

⑶侧墙处每延米水压力：根据水压力计算公式P=ρgh，可得侧墙上边缘每延米水压力为0.137 MPa，侧墙下边缘每延米水压力为0.203 MPa。侧墙水压力呈梯形分布，由0.137 MPa递增至0.203 MPa。

⑷侧墙处每延米土侧压力：根据朗肯土压力计算公式，计算可得侧墙顶部土侧压力为19.3 kPa，侧墙底部土侧压力为58.7 kPa，侧墙土压力呈梯形分布，由19.3 kPa递增至58.7 kPa。

⑸ 底板处每延米浮力：底板下表面标高取-14.17 m，水位按+7.79 m 的百年一遇水位计算，重力加速度g=9.8 m/s2，水的密度ρ=1.0×103kg/m3，根据水压力计算公式P=ρgh，底板底面浮力为0.215 MPa。

3 计算结果分析

将各个荷载输入模型中进行模拟计算，得出底板截面转换前后的沉管结构受力图。其中，底板截面转换后沉管结构的弯矩图、剪力图如图5所示。

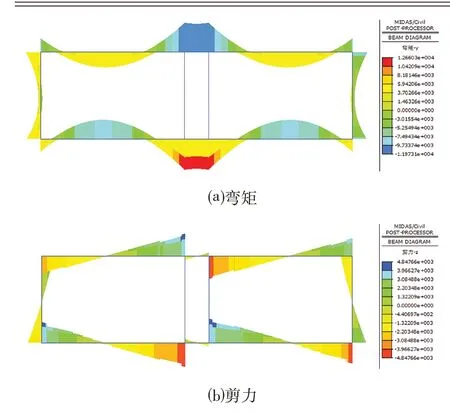
图5 截面转换后沉管结构弯矩及剪力Fig.5 Bending Moment and Shear Force of Immersed Tunnel Structure after Section Conversion

对计算结果进行分析：

⑴底板截面转换对沉管顶板受力的影响：截面转换前后，隧道两孔顶板跨中处弯矩变化值为51.2 kN·m，顶板中墙端弯矩变化值为196.8 kN·m，顶板侧墙端弯矩变化值为189.9 kN·m；顶板中墙端剪力变化值为30.1 kN，顶板侧墙端剪力变化值为35.4 kN。由以上数据可知，不论是弯矩还是剪力，其变化值占比最大为3.88%，可见底板的截面转换对隧道顶板的结构受力影响几乎可以忽略不计。

⑵底板截面转换对沉管侧墙受力的影响：截面转换前后，隧道侧墙顶板端弯矩变化值为203.4 kN·m，侧墙底板端弯矩变化值为421.1 kN·m；侧墙顶板端剪力变化值为106.3 kN，侧墙底板端剪力变化值为94.5 kN。变化值占比最大为3.91%，可见底板截面转换对隧道结构侧墙的影响也很小。

⑶底板截面转换对沉管底板受力的影响：截面转换后，隧道两孔底板跨中处弯矩增加了887.9 kN·m，增加幅度为13.36%；底板中墙端弯矩减小了825.1 kN·m，减小幅度为6.61%；底板侧墙端弯矩减小了534.3 kN·m，减小幅度为8.56%；底板中墙端剪力减小值为16.2 kN，减小幅度仅为0.33%；底板侧墙端剪力增加值为39.1 kN，增加幅度仅为0.97%。分析底板受力数据可以发现，底板截面转换对于底板跨中所受弯矩大小的影响较大，其次对底板中墙与侧墙两端的弯矩大小也有一定影响，而截面转换对于底板所受剪力的影响很小，可忽略不计。

通过以上对模拟结果数据的分析可以发现，由于沉管隧道结构所受的荷载不变，且顶板与侧墙的截面形状不变，因此顶板与侧墙处的结构内力大小几乎不受到底板截面转换的影响；而隧道底板处由于转换截面后底板结构自重减小，重力对地基反力的抵消作用减弱，导致地基反力对于底板竖直向上的作用力相对加大，使得底板跨中弯矩相应增大；而底板中墙端与侧墙端处撇脚位置由于底板跨中所分配承受的荷载相对变大，因此两处弯矩会有一定程度上的减小。

4 结论与建议

本文提出在沉管隧道底板左右两撇脚之间挖除一定量的混凝土，将原底板矩形截面形式转换成翼缘相连的倒置T 形梁形式，从而达到对结构减重，提高沉管浮运干舷高度的目的。使用MIDAS Civil 有限元分析软件对截面形式转换前后沉管结构受力进行分析，通过计算结果的对比得出以下结论：①底板截面形式转换后，顶板与侧墙处的结构内力大小几乎不受影响；②隧道底板跨中处由于结构自重减小，地基反力作用相对增强，导致底板跨中弯矩相应增大；③底板中墙端与侧墙端处由于底板跨中所分配荷载相对变大，因此两处弯矩有一定程度上的减小。在实际设计施工中，还可进一步对倒置T 形梁的截面参数进行优化，以期提高减重效果，同时满足结构的受力要求。