基于有限元分析的螺纹应力与旋合深度的研究

李维俊，汪小芳

(1.浙江同济科技职业学院，杭州 311231； 2.浙江运达风电股份有限公司，杭州 310012)

0 引言

由于进水球阀的结构外形比较复杂，所以分瓣结构的阀体1和阀体2基本采用铸件，并用双头螺杆连接。螺杆的一端旋合螺母，另一端与阀体2的内螺纹部分相配合。机械设计手册和企业设计基准均要求螺纹旋入铸件内螺纹的深度不得低于1.5倍的螺纹公称直径，经典计算结果只能得到螺纹旋合范围以内的平均应力，无法判定1.5倍旋合深度是否合适。螺纹旋合深度是否可以选1.25倍或是1.0倍，这个问题值得深入研究和探讨。

对于螺纹应力与旋合深度之间的关系，无法找到合适的经典计算和经验计算方法，只能采用有限元分析的手段进行。目前，多数学者对螺纹副的研究，主要集中在螺牙的应力分布状况和变形情况，并以螺纹牙根最大应力相等为优化目标，对螺纹牙高进行优化设计；螺纹牙根部的应力主要集中在内外螺纹啮合部分的第一扣的螺纹牙根部，距离此部位越远的螺纹所受应力变得越小；有限元分析软件可以采用简化模型对螺栓受轴向力后的应力变化进行模拟分析，结果显示简化模型的计算结果是有效的[1-3]。

但是，以前的研究很少关注到铸件内螺纹旋合深度不低于1.5倍螺纹公称直径这个点。文中在前人的研究基础上，建立铸件内螺纹和螺杆外螺纹有限元模型，通过有限元分析，根据螺纹应力分布状况的计算结果，分析了铸件内螺纹和合金钢外螺纹的螺牙应力与旋合深度之间的关系，为设备制造企业合理设置连接螺杆参数提供一定的参考。

1 进水阀主要参数

以某电站进水阀为例，其进水阀主要参数见表1，该进水阀为当时国内设计水头和公称直径综合参数最大的进水阀，在设计阶段无法找到相关业绩进行参考。由于进水阀的水头高、尺寸大，因此阀体连接螺杆参数的设计是否合理事关整个电站的运行安全。

表1 某电站进水阀主要设计参数

进水阀阀体分阀体1和阀体2，常规材料为ZG20Mn，通过高强度螺杆连接，螺杆常规材料选用锻34CrNi3Mo，如图1所示。阀体和螺杆常规材料的机械性能见表2。由于内外螺纹材料的机械性能相差较大，施加的预紧力较高，因此有必要关注螺纹旋合深度和预紧力两方面对铸件内螺纹强度的影响。

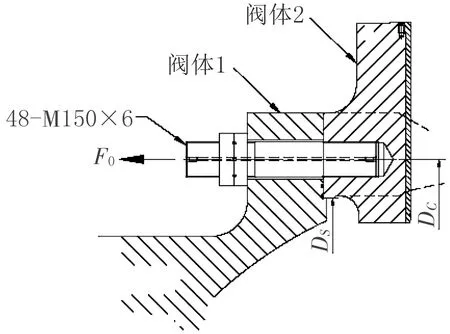
图1 阀体装配示意图

2 经典计算

螺杆的基本参数见表3。

正常工况螺杆所受轴向工作载荷F为

异常工况螺杆所受轴向工作载荷F′：

表2 材料性能对照表

表3 螺杆基本参数

出于对电站运行安全性考虑，项目合同要求重要部件连接螺栓的预紧力不低于工作载荷的2倍，所以取预紧力Fo=4 754 895 N，即：Fo/F>2。机械设计手册和企业计算标准规定在计算和校核螺杆强度时，一般按螺杆的螺纹谷径面积进行计算，以螺杆的许用应力进行校核。螺杆应力计算如式(1)～(3)：

正常工况工作应力：

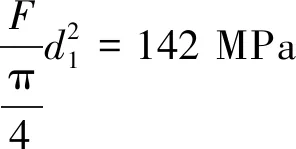
(1)

异常工况工作应力：

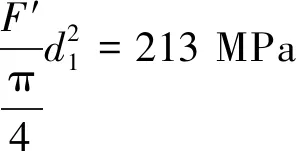
(2)

预紧应力：

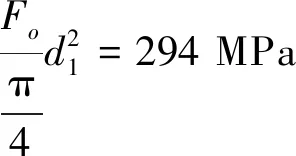
<σs=295 MPa。

(3)

从机械设计手册和企业计算基准的计算过程和计算结果中只能得到螺纹旋合深度(L)范围以内的平均应力，整个计算过程中都没有用到旋合深度(L)这个参数。关于铸件1.5倍公称直径的旋合深度与螺纹应力之间的关系，无法找到合适的经典计算和经验计算方法，只能采用有限元分析的手段进行。

3 有限元模型

3.1 几何模型

已有学者分别对螺纹副的2D模型和3D模型进行了有限元分析，计算结果表明2D轴对称模型对于螺纹副的载荷分布求解是非常有效的[4]。当不考虑螺纹升角时，内、外螺纹的啮合模型是轴对称的，可以在很大程度上降低有限元模型的网格数量，而不影响计算的精度。如图1所示，M150螺杆分布圆直径为Φ3 950，螺杆间距为258.3 mm，阀体2(内螺纹)部分取直径Φ300，高度取350 mm；阀体1取直径Φ300，高度按实际法兰的厚度；螺杆和螺母均按实际尺寸建立轴对称2D几何模型，如图2所示。

3.2 网格划分

采用八节点四边形单元对2D模型进行自由网格划分；对内、外螺纹啮合部分采用单元边长0.05～0.1 mm的网格。网格大小经过不断地调试，单元大小满足静力学求解要求。内、外螺纹单元类型均为轴对称二阶四边形单元，如图3所示，由83 144个单元和262 064个节点构成。

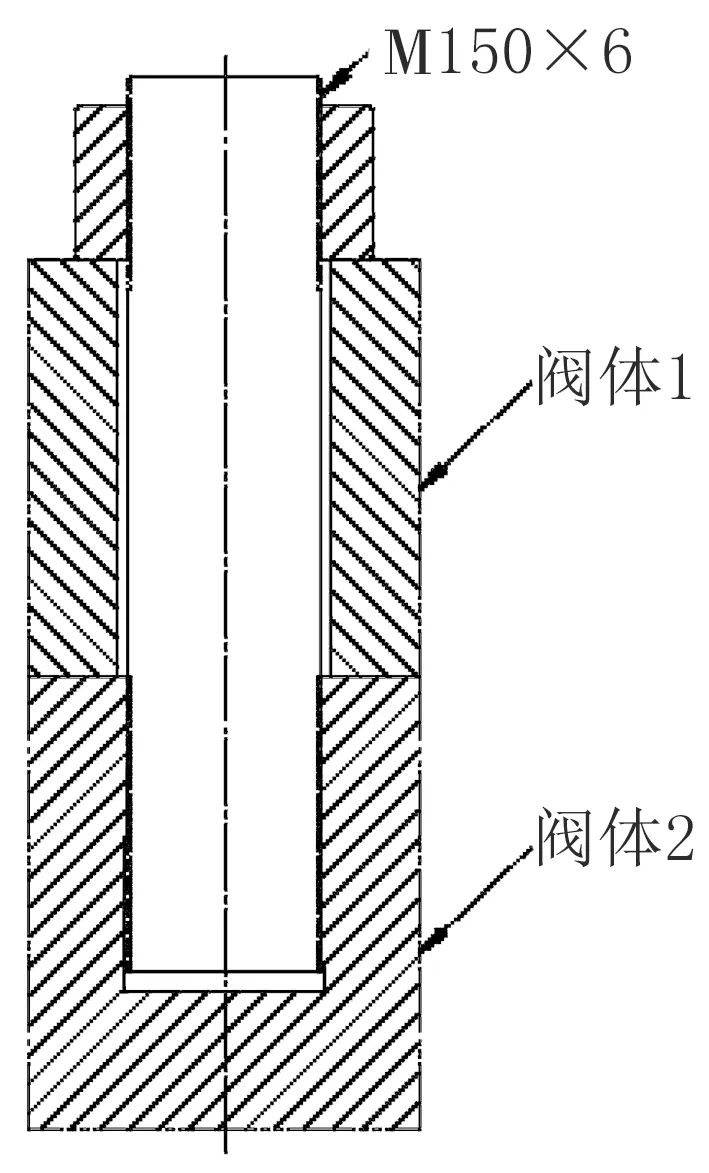
图2 几何模型

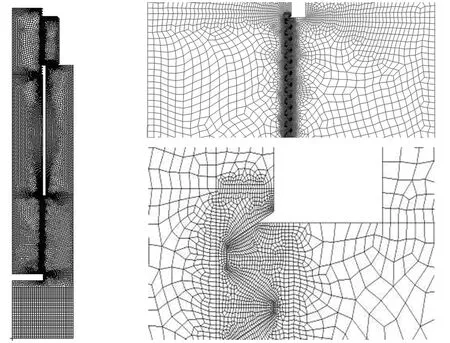
图3 有限元模型

3.3 边界条件的设置

对螺杆施加预紧力，即Fo=4 754 895 N；由于建立局部模型模拟阀体2，因此对阀体2内螺纹部分的底面施加固定约束。阀体2、阀体1、螺母相互之间建立摩擦接触；螺杆与螺母之间的螺纹副、螺杆与阀体2之间的螺纹副也均为摩擦接触；所有摩擦接触的摩擦因数均为0.15。

4 计算结果

4.1 应力分布

经过仿真计算，2D轴对称单元模型的Von Mises应力分布状况如图4所示，将螺纹旋合部位放大后，如图5所示。

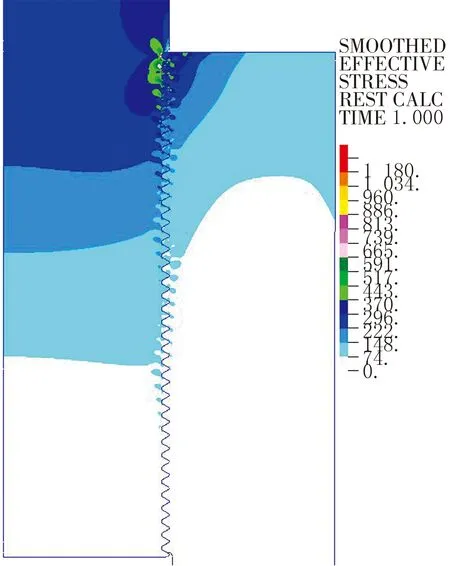
图4 Von Mises应力云图

图5 Von Mises应力云图(局部)

4.2 结果分析

由于内螺纹的牙型不完整，实际内螺纹的第1扣螺牙也达不到整圈，因此内螺纹只从第2扣螺牙开始进行分析。从图4～5中可以清晰地看到外螺纹前3扣和内螺纹前四扣螺牙所受的应力最大。随后，螺纹应力随着旋合深度的增加，内外螺牙的应力迅速减小，距离螺纹第1扣越远，螺牙的应力越小。这与以往学者的研究吻合。

从图5中可以看到内外螺牙在接触的一侧出现应力集中，应力跨度比较大，应力分布比较复杂。因此取内外螺牙接触面背侧的螺纹中径附近节点的应力进行数据分析，其节点位置如图6所示。

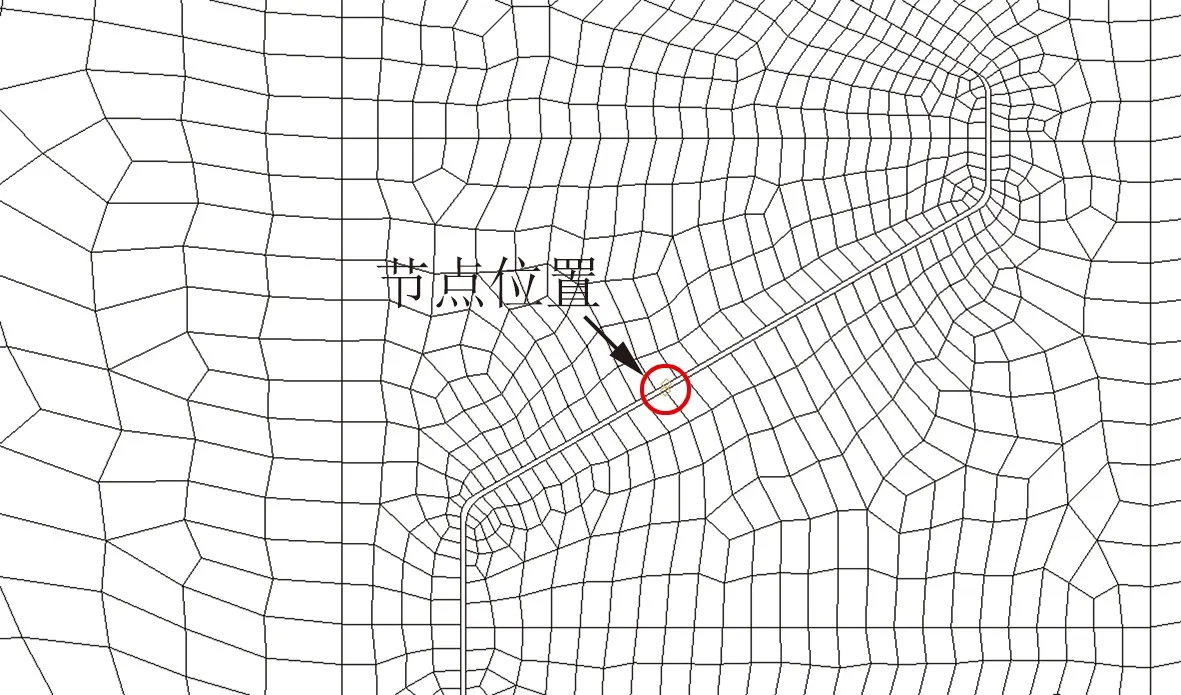
图6 取螺牙应力节点位置

内外螺纹在该节点处的应力与旋合牙数的对应曲线如图7所示。

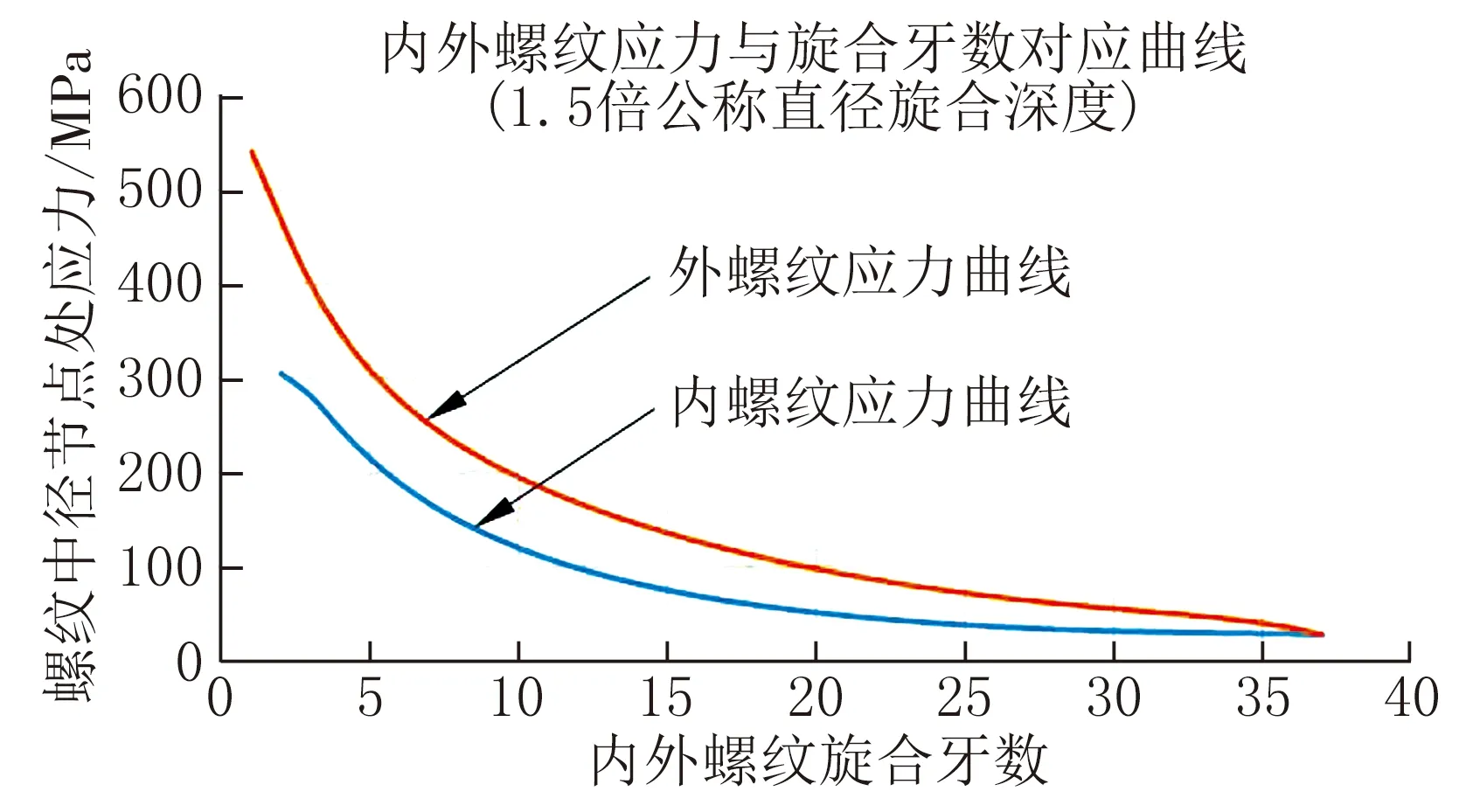
图7 内外螺纹应力与旋合牙数对应曲线

从图7的曲线中可以获得的信息：

1)外螺纹应力比内螺纹应力高，第2扣内外螺牙应力相差162 MPa。

2)外螺纹前几扣应力下降得比较快，第6扣应力是第1扣螺牙应力的51%。

3)内螺纹前几扣应力比外螺纹前几扣应力下降得缓慢，第8扣是第2扣螺牙应力的49%。

4)内外螺纹在第18扣螺牙之后的应力占比均低于20%。

5)内螺纹在22扣之后的应力几乎是一条水平线。

4.3 不同旋合深度计算结果

重复前述过程，施加相同边界条件，继续考查不同旋合深度条件下，内外螺纹应力分布状况。经过计算，得到旋合深度分别为192 mm和150 mm时的内外螺纹应力分布，分别如图8和图9所示。

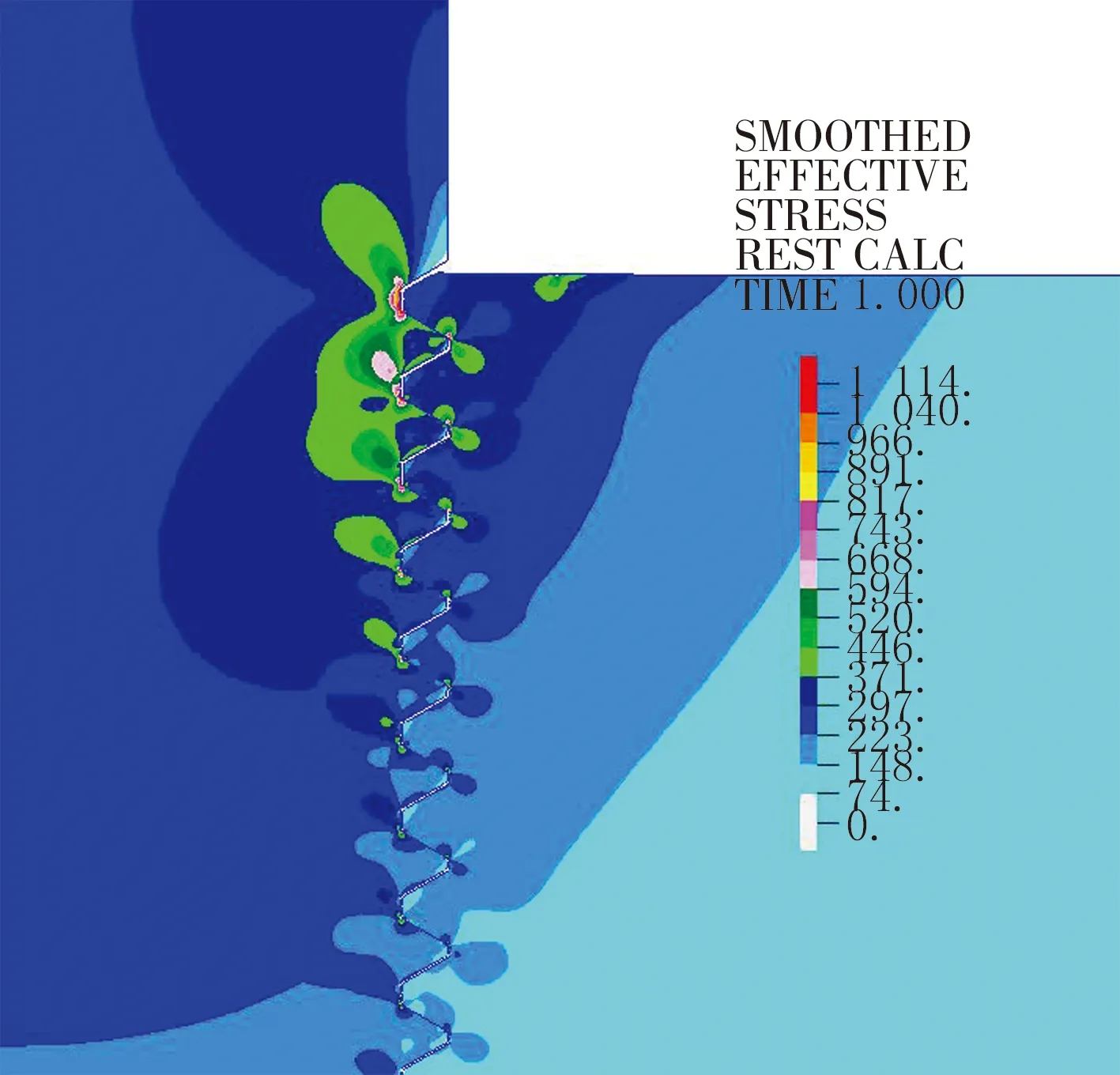
图8 旋合深度为192 mm时的应力云图

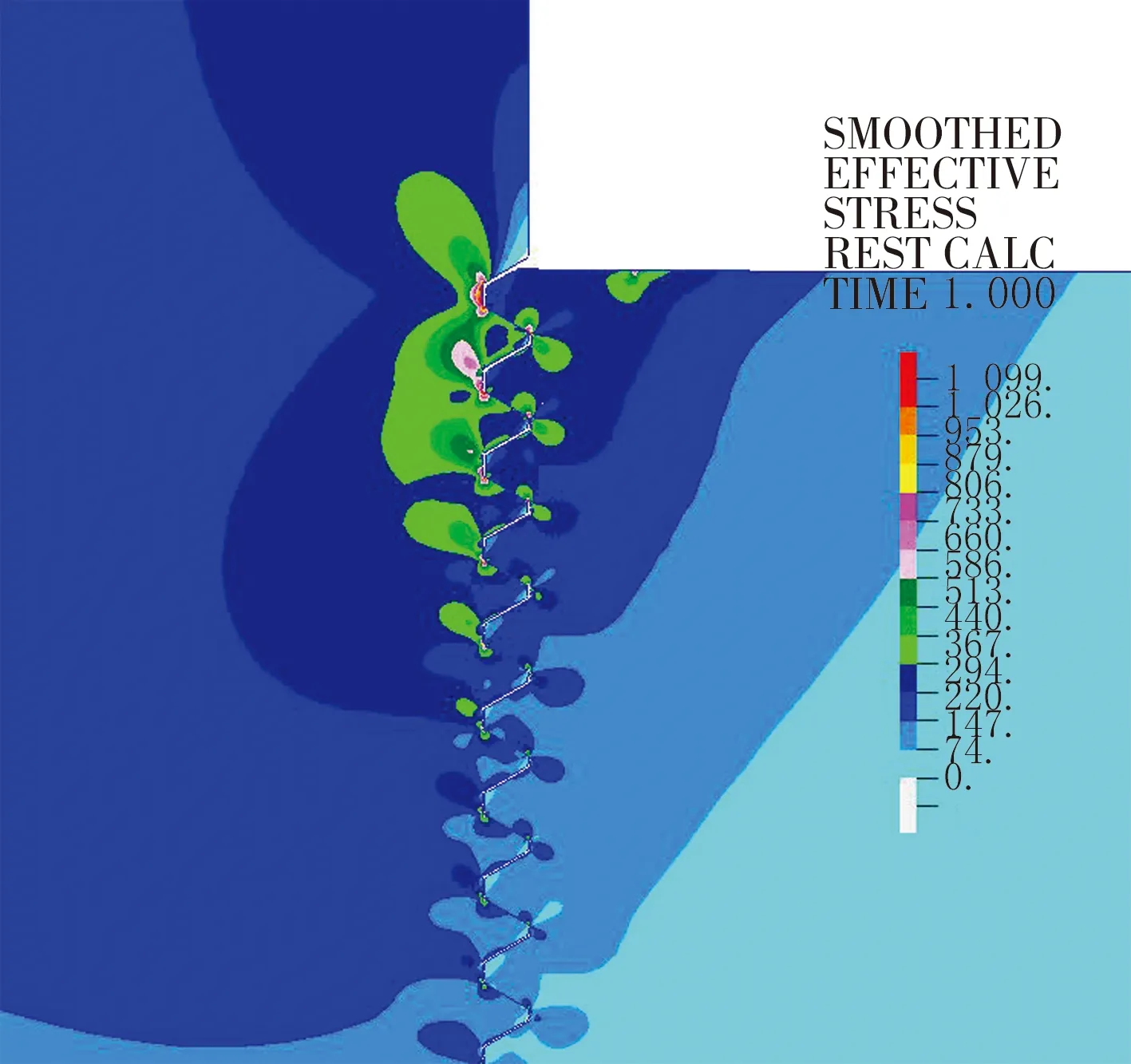
图9 旋合深度为150 mm时的应力云图

旋合深度分别为192 mm和150 mm时，内外螺纹应力分布状况和分布特点与旋合深度为225 mm时类似。

4.4 计算结果比较

225 mm、192 mm和150 mm 3种旋合深度在同一边界条件下，前8扣内外螺牙应力见表4；由于内螺纹材料的机械性能远低于外螺纹材料，所以重点分析内螺纹，前8扣内螺牙应力与旋合牙数对应曲线如图10所示。

不同旋合深度下，内螺纹第2扣中径节点处的应力与铸件材料的屈服极限和极限强度对照表，见表5；其螺牙应力与旋合深度对应曲线如图11所示。

5 结论

通过对不同旋合深度在同一边界条件下的计算结果进行分析，可以得到的结论：

1)旋合深度越深螺纹所受应力越小，呈递减趋势。

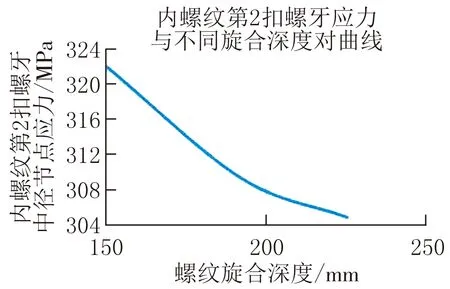
图11 第2扣螺牙应力与旋合深度对应曲线

2)1.5倍和1.25倍旋合深度下的内螺纹应力相差不大。

3)294 MPa预紧应力下，已经超过铸件ZG20Mn材料的机械性能的极限。

这些计算结果可为以铸件为内螺纹时，施加预紧力条件下，设计螺杆参数时提供一定的参考。由于计算模型为2D轴对称模型，无法获得螺杆受到弯矩时的螺纹应力。如果要获取更真实、受力状态更复杂条件下的螺纹应力，需要进一步对螺杆进行3D仿真计算。