考虑执行机构饱和的迎角跟踪控制
高 丽,曲志刚,梅 丹
(海军航空大学,山东青岛 266041)
0 引言
动态逆是飞行控制领域中应用较为广泛的非线性方法[1-10]。基于比例积分及指令滤波器的比例微分结构的动态逆控制,在不确定性不严重的情况下对提高系统鲁棒性有一定作用,但是鲁棒性还需进一步提高。解决动态逆鲁棒性问题常用的方法有鲁棒控制和自适应误差补偿。鲁棒控制方法,如内环使用动态逆,外环使用结构奇异值、QFT、μ 综合等鲁棒设计方法进行综合设计[11-14];误差补偿方法,即使用神经网络自适应、模糊自适应等方法对误差进行补偿[4-9]。也有文献应用L1自适应控制有效补偿不确定性的影响[3,10,15]。
考虑到执行机构饱和对动态逆控制的影响,本文主要研究如何将基于动态逆的自适应控制方法应用于迎角跟踪控制上,并且重点研究执行机构饱和特性对动态逆自适应控制的影响。
1 动态逆控制L1 自适应补偿
考虑如下二阶系统:

式(1)中:x为系统的状态量;δ为控制输入量;x,ẋ∈ℝn,δ∈ℝm,m≥n。引入伪控制量v,可得系统的状态量与伪控制量的线性关系:

伪控制量是由期望控制输入量δcmd得到的动态响应:

f(x,ẋ,δ)是系统的精确非线性模型,而f-1(x,ẋ,δ)是其精确逆模型。由于飞机模型的复杂性,一般在建模时难以得到精确的动力学模型,所以,计算中用近似模型f̂(x,ẋ,δ)代替,故动态逆误差可表示为:

式(6)中,xm表示理想跟踪状态,该模型由有界的、线性时变(或时不变)的参考指令xcmd驱动。式(6)可以表示为如下状态空间形式:

为了保证跟踪误差的稳定性,在伪线性系统设计中,可采用比例微分控制器;如果存在稳态误差,那么可采用积分环节加以消除。控制结构如图1所示[16]。

图1 具有L1 自适应补偿的动态逆结构Fig.1 Dynamic inversion with L1 adaptive compensation
由于飞行包线内飞行条件变化剧烈,纵侧向耦合严重,且具有外界干扰的影响,逆误差函数是非常复杂的非线性函数,很难用具体的解析表达式描述。而动态逆控制方法应用的条件是对系统数学模型有准确的了解,因此,逆误差无法由动态逆控制方法自动消除。为了消除逆误差,在动态逆控制器中增加自适应控制环节,其输出信号vad用于抵消逆误差及不确定性的影响。于是伪控制量由3部分组成:

为了方便进一步分析,系统满足如下假设[17]。
假设1(f(t,0 )的一致有界性):对于任意δ>0,存在Lδ,B>0,使得‖f(t,x1)-f(t,x2)‖∞≤Lδ‖x1-x2‖∞,∀‖x‖∞≤δ<∞;|f(t,0) |≤B,∀t≥0。
假设2(偏导数的半全局一致有界性):f(t,x)在论域内是连续的,而且对于∀δ>0 ,存在dfx(δ)>0 和dft(δ)>0,使得对任意‖x‖∞≤δ<∞,f(t,x)关于x和t的偏导数是分段连续且有界的,

注1:该引理使得非线性函数f(t,x)能够使用2个时变参数线性参数化。条件比使用神经网络逼近要严格,但是相比于神经网络逼近又具有以下优点:不必选择基函数、能得到半全局结果和不必调整参数即可保证瞬态性能。
假设Δ(x,ẋ,δ)满足上述参数线性化条件,那么自适应信号vad可由L1自适应控制器[17]生成。将Δ(x,ẋ,δ)=θ(t)‖X(t)‖∞+σ(t)代入式(13),那么

根据L1自适应控制理论,设计C(s)为合适的低通滤波器,要求C(s)为稳定的严真系统,且C(0)=1。L1控制器由式(15)∼(17)组成,且满足L1-范数上界约束。预测误差动态:
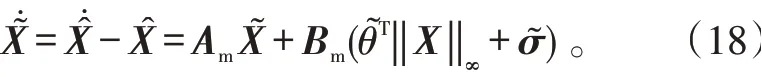
式(18)中:估计误差θ͂=θ̂-θ,σ͂=σ̂-σ。考虑如下Lyapunov候选函数:

相应的,闭环系统逼近L1参考系统(假设参数精确已知):

参考系统控制信号:

式中,Δref≜Δ(Xref,t)。满足L1-范数上界约束,那么Xref有界。
2 伪控制保护改进
非线性动态逆除了须改善鲁棒性以外,还有个重要问题,就是执行机构的饱和特性对系统稳定性和性能的影响。伪控制保护(Pseudo Control Hedging,PCH)的概念由Johnson 提出[18],目的是针对输入特性(如作动器位置限制、作动器速率限制及线性输入动态)补偿参考模型信号,避免执行机构进入饱和。NDI对飞行器动态求逆,未包括作动器的输入特性,这是由于一旦考虑则使得动态逆设计变得非常复杂。Holzapfel[13]将该概念应用于基于NDI的自适应控制中。
考虑二阶系统(1),假设系统方程能够写为仿射形式:

由于控制执行机构的饱和非线性特性,使得真实控制位置δact与指令控制位置δcmd不同。下一步,基于真实控制位置δact,计算虚拟输入的估计值v̂:

将指令虚拟输入减去估计值得PCH补偿信号vh:

该信号作为补偿信号反馈到参考模型中,如图2所示。

图2 伪控制保护结构配置Fig.2 Setup of the Pseudo Control Hedging structure
从图2 可以看出,PCH 将指令信号减小至作动器动态可以到达的幅值。该结构对NDI来说,优点是当计算虚拟输入的估计值ν̂和PCH 信号νh时,自动地考虑辨识动力学模型和控制舵面偏转的破坏信息,从而有效避免了作动器饱和。但是可能存在|δcmd|=|δact|=δmax的情况,即系统实际已经进入饱和后,PCH信号才起作用。


注2:引入虚拟位置约束的目的主要是保证稳定性并限制性能下降。引入正常数λ的主要目的是为作动器位置约束定义“安全区域”,当指令控制进入该区域时,即开始修正指令控制,使得所有时刻作动器位置均不会饱和。
将指令虚拟输入减去估计值得到补偿信号:

当指令控制信号进入“安全区域”但是还未达到饱和时,保护信号开始工作,引入到参考模型中修正指令控制,而不必等到进入饱和时才开始修正,选择合适的λ能够使得所有时刻作动器位置均不会进入饱和。具有保护信号的参考系统模型,如图3所示[5]。
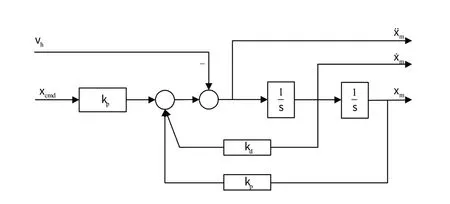
图3 具有保护信号的参考系统模型Fig.3 Reference model with hedging signal
由图3 知,引入保护信号vh,改变了参考模型动态特性,故还需研究参考模型的稳定性。定义参考模型指令跟踪误差ecm=[xcmd-xm,ẋcmd-ẋm]T,表示参考模型的状态xm与指令输入xcmd之间的误差,可得到如下结论[5]。
对ecm求导,得参考模型指令跟踪误差动力学方程:


注3:为保证参考模型指令跟踪误差的稳定性,伪控制保护信号vh应尽量小。
3 仿真
将上述基于L1自适应补偿的动态逆控制方法应用于某舰载机的六自由度全量非线性模型,通过研究对动态逆慢回路中的迎角跟踪控制,以提高系统的鲁棒性和抗干扰能力。对于L1自适应控制器,设自适应增益Γ=1 000,低通滤波器C(s)=15 (s+15) 。仿真初始条件:初始迎角4.27°,指令为方波输入;并且具有如下参数不确定性:俯仰静不稳定性增加20%,俯仰阻尼降低20%;未知时变干扰sin( πt4 )。
由图4仿真结果可以看出,采用自适应补偿后,超调下降,迎角曲线几乎与参考输出曲线重合,表明设计的自适应补偿可改善系统鲁棒性,并且自适应估计值均有界。


图4 迎角跟踪L1 自适应补偿Fig.4 Compensation with L1 adaptive control
但是上述仿真未考虑执行机构的饱和特性,升降舵偏转进入饱和,如图5 所示,并且舵面出现剧烈抖动。选取λ=0.6,采用改进PCH 信号补偿,如图6 所示,迎角跟踪性能几乎不受影响,升降舵偏转不会进入饱和,并且舵面抖动得到抑制,表明设计补偿信号的有效性。

图5 无PCH补偿的迎角跟踪Fig.5 Angle of attack tracking without hedging signal

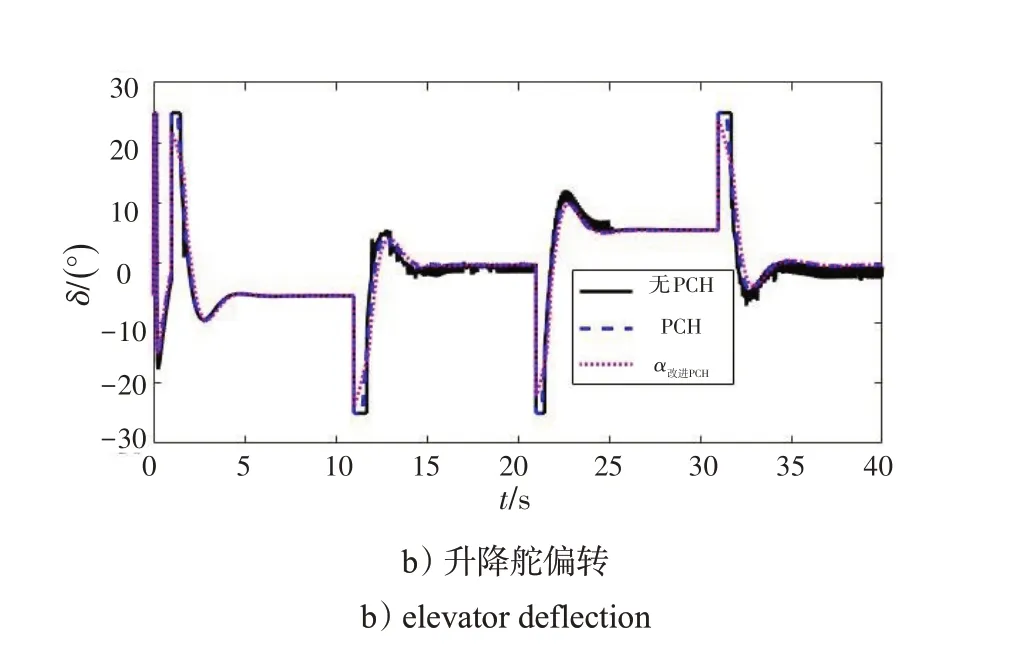
图6 具有改进PCH(λ=0.6)的迎角跟踪Fig.6 Angle of attack tracking with hedging signal(λ=0.6)
4 结论
为了进一步改善鲁棒性,基于非线性动态逆控制器设计L1自适应补偿环节,提出了1种改进的伪控制保护方法,产生伪控制补偿信号修正参考输入信号,使得执行机构在任何时刻都不会进入饱和。上述研究表明:为保证参考模型指令跟踪误差的稳定性,伪控制保护信号vh应尽量小;仿真结果验证了具有伪控制保护的L1自适应补偿对迎角跟踪控制的有效性。

