异构型样本次序统计量的排序性质——2013年至今的研究进展及展望

张 靖，方 睿

（1.香港大学统计与精算学系，香港 999077；2.汕头大学数学系，广东 汕头 515063）

0 引言

次序统计量在诸如统计推断、拟合优度、可靠性理论、经济金融、运筹学、保险精算、拍卖理论等研究领域中具有十分重要的研究价值.记Xi:n表示来自随机样本X1，…，Xn的第i小次序统计量，随机样本服从某些具体的分布模型，样本彼此之间相互独立或者具有某些相依性结构.在过去的三四十年间，国内外多位学者围绕次序统计量的随机比较问题进行了深入的研究，其中有大量的工作建立在样本独立同分布的假设之上.由于相依或异构型样本的分布理论较为复杂，文献中只有为数不多的研究结果.独立异构型样本的次序统计量随机比较研究可参阅文献[1-4].相依样本的次序统计量随机比较研究可参阅文献[5-7].

近年来已有若干文献针对不同时期次序统计量随机比较的研究进行了阶段式的回顾综述，如 Kochar[8]，Boland 等[9]，Boland 等[10]，Khaledi和 Kochar[11]，Kochar和 Xu[12]以及Balakrishnan和Zhao[13]分别对1998之前、2002之前、2007之前以及2013年之前的研究工作进行综述.从2013年之后，得益于分布模型、相依性理论、优化序理论的发展，次序统计量的随机比较研究进入新的阶段，涌现出很多新的成果，也带来新的挑战.本文对2013年至今十年间该领域的重要研究结果进行梳理和综述，并力争对下一个十年的研究方向做部分展望.

本文的结构编排如下：第一节中对若干重要概念定义进行介绍，第二节主要关注失效率参数的有关研究结果，第三节围绕反失效率参数的情形进行综述，第四节回顾了尺度参数的相关研究结果，第五节针对形状参数进行文献梳理，最后在第六节中讨论了几个仍未解决的重要问题，展望了未来的研究方向.

1 预备知识

本节对一些本文将用到的重要概念进行回顾，包括随机序、优化序、联结函数等.约定后文中出现的“递增”表示单调非减，“递减”表示单调非增.

1.1 随机序

定义1.1假设X和Y是两个非负的随机变量，其分布函数分别为F，G，分布函数的

右连续逆函数分别为F－1，G－1，生存函数分别为，，密度函数分别为f，g.

（iii）若对 x＞0，G（x）/F（x）关于x是递增的，则称X依反失效率序小于Y，记做X≤rhY；

（iv）若对0＜a≤b＜1，F－1（b）－F－1（a）≤G－1（b）－G－1（a），则称X依色散序小于Y，记做X≤dispY；

（v）若对 x＞0，G－1F（x）/x关于x是递增的，则称X依星序小于Y，记做X≤*Y；

（vi）若对x∈∪{supp（X），supp（Y）}，f（x）/g（x）关于 x 是递减的，其中 supp（X）＝{x:f（x）＞0}表示随机变量X的支撑集，则称X依似然比序小于Y，记做X≤lrY.

更多关于随机序的内容可参考专著[14-15].

1.2 优化序

定义 1.2 设 x＝（x1，…，xn）∈Rn，y＝（y1，…，yn）∈Rn，令 x1:n，…，xn:n是 x 的递增排序.

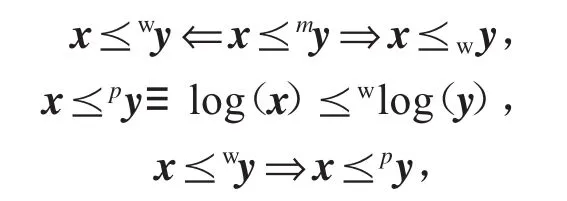
其中logx是x取对数后得到的向量.更多关于优化序的内容可参见专著的研究结果[16].

1.3 联结函数

Sklar首次提出联结函数用于刻画随机变量之间相依性结构[17]，其定义如下：

定义1.3假设随机向量X＝（X1，…，Xn）的单变量边际分布函数为F1，…，Fn，边际生存函数为，则存在函数 C:[0，1]n[0，1]和，使得对 xi，1≤i≤n，X的联合分布函数可表示为

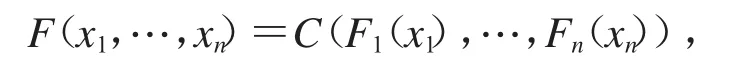
X的联合生存函数表示为

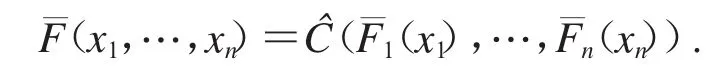
C（u1，…，un）和分别称为 X 的联结函数和生存联结函数.

1.3.1 Archimedean联结函数

联结函数的族类很多，其中一类具备良好解析性质并且涵盖众多常用联结函数的族为Archimedean联结函数族[18].

定义 1.4 对 ui∈（0，1），1≤i≤n，若存在 ψ:［0，＋∞）（0，1］，满足 ψ（0）＝1，ψ（＋∞）＝0，且（－1）jψ(（j)x）≥0，j＝0，1，…，n－2，同时（－1）n－2ψ(n－2（)x）为递减凸函数，则

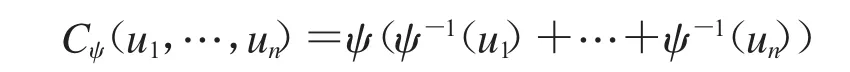
为Archimedean联结函数，ψ称为该联结函数的生成元.

Archimedean联结函数族包含许多著名的联结函数，包括独立（乘积）联结函数，Clayton联结函数，Frank联结函数等.特别地，生成元ψ（t）＝e－t对应独立的情况，相应的Archimedean联结函数表示为

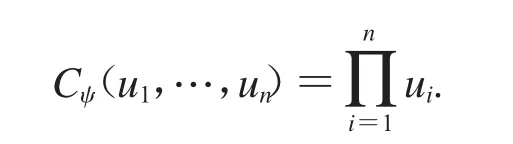
1.3.2 FGM联结函数

另一类被广泛关注和应用的联结函数族为Farlie-Gumbel-Morgenstern（FGM）联结函数族[19].

定义1.5含有n个变量的FGM联结函数的表达式为

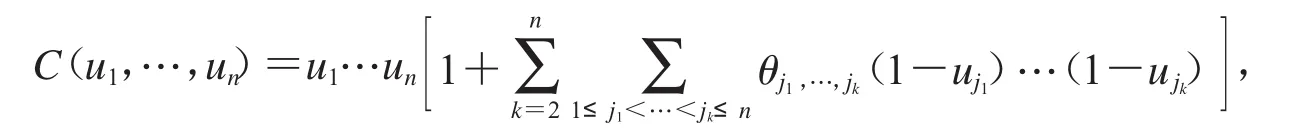
其中对 j1，…，jk，－1≤θj1，…，jk≤1.本文中定理结果引用以下简化版本：

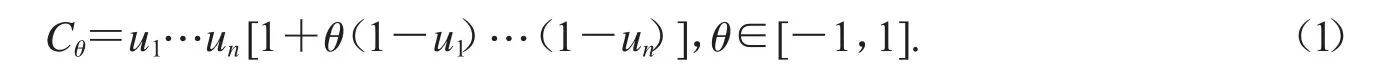
1.4 Schur凸性与Schur凹性

Marshall等[16]详细回顾探讨了优化序在函数不等式等方面的应用，其中重点包含一类与优化序密切相关的函数性质：Schur凸性和Schur凹性.

定义 1.6 设 I是 R 上的开区间，x＝（x1，…，xn）∈Rn，y＝（y1，…，yn）∈Rn，若存在一个函数ϕ:InR，使得

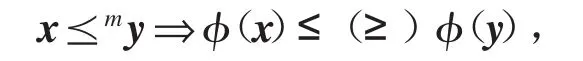
则称ϕ是In上的Schur凸（Schur凹）函数.

1.5 超可加性

在涉及次序统计量排序性质的研究中，还有一类具有特殊性质的函数经常被使用.定义1.7 设I是R上的开区间，f为定义在I上的函数.若对 x，y∈I，有f（x＋y）≥f（x）＋f（y），则称 f是 I上的超可加函数.

2 失效率参数

本节主要回顾关于失效率参数对次序统计量排序结果影响的研究.文献中围绕失效率参数的研究主要从比例失效率模型入手，具体的：如果随机变量X1，…，Xn服从比例失效率模型，则对于i＝1，…，n，Xi的生存函数可以表示为

2013年之前的研究主要基于独立的情况讨论指数分布、Weibull分布以及一般比例失效率模型相关结果[13].近十年来陆续有文献围绕相依的情况展开研究，如Li和Fang[5]假设随机变量X1，…，Xn服从比例失效率模型，采用Archimedean联结函数刻画样本间的相依性结构，研究了最大次序统计量的随机比较问题.记随机样本为X＝（X1，…，Xn），考虑，则 X 的联合生存函数为其中 ψ为Archimedean联结函数的生成元.针对最大次序统计量，Li和Fang得到如下通常随机序的比较结果[5]：

除了上述结果，Li和Fang还给出了使得定理2.1结论成立的其他充分条件，同时也讨论了色散序的结果[5].类似地，Fang等讨论了最小次序统计量间存在通常随机序的充分条件[6]：

此外，Fang等还给出了若干最小次序统计量间存在色散序、星序的充分条件，同时也得到了第二小次序统计量随机比较的结果[6].对于具有FGM联结函数的比例失效率样本，Wang和Fang讨论了第二小、第二大和最大次序统计量的结果[20]：

定理2.3：假设X1，…，Xn的联结函数为（1）中所给的参数为θ的FGM联结函数且Xi～PH（，αi），Y1，…，Yn具有相同的联结函数且Yi～PH（，βi），其中－1≤θ≤1.若（α1，…，αn）m（β1，…，βn），则有 Xn:n≤rhYn:n.

一些文献也关注相依情况下特殊分布的随机比较结果，Barmalzan等针对具有相同相依结构的布尔XII型样本，讨论了失效率参数异构性对最小、最大次序统计量随机大小比较的影响[21].在独立的假设下，近十年来一些文献开始关注失效率参数异构性对Pareto分布和其他分布的随机比较的相关研究[22-25]，同时也有部分文献进一步补充了指数分布、Weibull分布关于似然比序等随机序的结果[26-30].

3 反失效率参数

本节主要回顾关于反失效率参数对次序统计量排序结果影响的研究.文献中围绕失效率参数的研究主要从比例反失效率模型入手，具体的：如果随机变量X1，…，Xn服从比例反失效率模型，则对于i＝1，…，n，Xi的分布函数可以表示为

其中F（x）是某个随机变量X的分布函数，记Xi～PRH（F，μi）.对于具有形如（3）式的分布函数的随机变量，我们称μi为该随机变量分布的反失效率参数.常见具有反失效率参数的分布有广义指数分布，其分布函数为（1－exp（－λx））α，其中α为反失效率参数；复合指数型分布族，如指数型伽马分布，其分布函数为（1－（λx＋1）exp（－λx））θ，其中θ为反失效率参数.

2013年以来的研究主要围绕具有反失效率参数的特殊分布，针对一般反比例失效率模型的研究较为零星分散，Torrado假设独立随机变量X1，…，Xn服从比例反失效率模型，针对最小次序统计量，得到如下失效率序的比较结果[31]：

定理3.1：假设 X1，…，Xn相互独立且 Xi～PRH（F，ai），Y1，…，Yn相互独立且Yi～PRH（F，bi）.若（a1，…，an）W（b1，…，bn），则有X1:n≥hrY1:n.

类似地，Zhao等给出了最大次序统计量间存在反失效率序的充分条件[32]：

定理3.2：假设 X1，…，Xn相互独立且 Xi～PRH（F，ai），Y1，…，Yn相互独立且Yi～PRH（F，bi）.若（a1，…，an）W（b1，…，bn），则有Xn:n≥rhYn:n.

同样考虑独立样本的情况，Bashkar等将定理3.2中关于反失效率参数的条件弱化后，得到样本最大次序统计量基于似然比序的结论相似的比较结果[33].

Fang等[6]采用Archimedean联结函数刻画样本间的相依性，研究了比例反失效率模型中反失效率参数的异构性对最大次序统计量的作用.具体的，考虑随机样本为X＝（X1，…，Xn），X～PRH（F，μ，ψ），则 X 的联合分布函数为其中ψ为Archimedean联结函数的生成元.针对最大次序统计量，可以得到如下通常随机序的比较结果：

定理3.3：假设 X～PRH（F，a，ψ1）和 Y～PRH（F，b，ψ2），（i）若 ψ1或 ψ2为对数凸函数且 ψ1－1ψ2是超可加函数，则由 aWb可得 Xn:n≤stYn:n；（ii）若ψ1或 ψ2为对数凹函数且ψ2－1ψ1是超可加函数，则由aWb可得Xn:n≥stYn:n.

除了上述结果，Fang等还给出了若干最大次序统计量间存在色散序、星序的充分条件，同时也得到了第二大次序统计量随机比较的结果[6].对于具有FGM联结函数的比例反失效率样本，Wang和Fang得到了如下结果[20]：

定理3.4：假设X1，…，Xn的联结函数为（1）中所给的参数为θ的FGM（生存）联结函数且Xi～PRH（F，λi），Y1，…，Yn具有相同的（生存）联结函数且Yi～PRH（F，ηi），其中－1≤θ≤0.若（λ1，…，λn）W（η1，…，ηn），则有Xn:n≥stYn:n（X1:n≥stY1:n）.

其他关于反失效率参数异构性对特殊分布随机比较的研究可以参见[20，31，33-37].

4 尺度参数

本节主要回顾关于尺度参数对次序统计量排序结果影响的研究.文献中围绕尺度参数的研究主要从尺度模型入手，具体的：如果随机变量X1，…，Xn服从尺度参数模型，则对于i＝1，…，n，Xi的分布函数可以表示为

其中F（x）是某个随机变量的分布函数.对于具有形如（4）式的分布函数的随机变量，我们称μi为该随机变量分布的尺度参数.很多分布的一些参数格式下，某些参数可以同时看做失效率参数或尺度参数，如分布函数为1－exp（－μx）的指数分布；或者反失效率参数或尺度参数，如分布函数为exp（－（μx）－1）的Frechet分布等.这种情况的参数本文中分别归为失效率参数或反失效率参数.

2013年以来围绕具有尺度参数的特殊分布的研究不多.Li等[38]假设随机变量X1，…，Xn服从尺度参数模型，采用Archimedean联结函数刻画样本间的相依性结构，记随机样本为 X＝（X1，…，Xn），考虑 X～S（F，μ，ψ）和两种情形，分别对应 X1，…，Xn的联合分布函数为以及X的联合生存函数为的情况，其中ψ为Archimedean联结函数的生成元.分别针对最小、最大次序统计量，获得了如下通常随机序的比较结果：

定理4.3：假设 X～S（F，λ，ψ1），Y～S（F，μ，ψ2），ψ1或 ψ2为对数凸函数，ψ1－1ψ2是超可加函数，若有（i）λPμ且F具有递减比例反失效率；或者（ii）λWμ且F具有递减反失效率，则有Xn:n≤stYn:n.

除了上述结果，Li等[38]还给出了若干最小次序统计量间存在色散序、星序的充分条件.在独立的假设下，Wang针对一般尺度模型，讨论了最大次序统计量间存在似然比序的充分条件[39]；Fang等[40]和Zhang等[41]先后将Li等[38]中的尺度参数模型推广到同时具有失效率参数或者反失效率参数的尺度参数模型，并讨论了尺度参数、失效率参数或反失效率参数的异构性对最小、最大次序统计量随机大小的影响.

5 形状参数

除了前述三种参数（失效率参数、反失效率参数、尺度参数）之外，有些概率分布族还会依赖其它参数，由于这些参数通常对分布族的密度函数及分布函数的形状具有直接影响，可统称为形状参数.如贝塔分布、布尔XII型分布、Dagum分布及推广的指数分布等均具有形状参数.由于不同分布族的形状参数数学性质不同，围绕形状参数的研究多假设总体服从某一特定分布.

2013年之前的研究多围绕贝塔分布开展，近十年来陆续有文献关注其它分布形状参数的作用.Dagum分布的分布函数具有形式F（x）＝（1＋λx－δ）－β，其中δ即为形状参数，记为Da（λ，δ，β）.Fang等考虑总体服从Dagum分布的独立随机样本，在另外两个参数固定的情况下，得到以下结果[36].

定理5.1：假设 X1，…，Xn相互独立且 Xi～Da（λ，δi，β），Y1，…，Yn相互独立且Yi～Da（λ，δ*i，β）.若，则有 Xn:n≥stYn:n.

定理5.2：假设X1，…，Xn的生存联结函数为式（1）中所给的参数为θ的FGM联结函数且 Xi～Γ（αi，β），Y1，…，Yn具有相同的生存联结函数且 Yi～Γ（ηi，β），其中α1≥α2≥…≥αn≥1，η1≥η2≥…≥ηn≥1.若（α1，…，αn）m（η1，…，ηn），则有 X1:n≥stY1:n.

除了上述两个重要结论之外，更多关于形状参数异构性对最小、最大次序统计量随机大小影响的最新研究结果可以参见[36，42-43].

6 总结

本文通过文献所研究的参数类型，按照失效率、反失效率、尺度以及形状参数进行分类，系统综述了异构型样本次序统计量随机比较的研究进展.受限于篇幅和笔者水平，主要围绕单一参数的影响，回顾了比较重要或者考虑半参数总体分布的研究结果.一些分布族往往具有多个参数，相比单一参数，多个参数的异构性之间的交互作用对最小、最大次序统计量随机大小的影响机制更为复杂，有关多参数异构性作用的研究可以参阅文献[24-25，31，37，40，44-45].此外，除了本文考虑的4种参数类型外，有为数不多的文献研究了位置参数的作用[46].受限于分布函数或生存函数表达式的复杂性，除了最小、最大次序统计量外，有关其余次序统计量的结果绝大多数基于独立样本的假设下[47]，而相依样本的随机比较研究结果很少，并且为数不多的结果仅仅讨论了第二小、第二大次序统计量，相关结论零星散布于最小、最大次序统计量的文献中[6，20].此外，随着联结函数理论的发展，近年来有越来越多研究将相依性一并纳入，但多采用Archimedean联结函数或FGM联结函数[20，30，41-42，48-49].对于具有更多相依结构的样本第二小、第二大及其它次序统计量、以及其它更多类型参数的随机比较问题，仍有待进一步的研究.