基于局部模体分布相似性的重叠社区发现算法
杨贵,徐乾
(山西大学 计算机与信息技术学院,山西 太原 030006)
0 引言
复杂系统中个体间通过相互作用形成功能模块,因此通常将现实中的复杂系统抽象为复杂网络,节点表示系统个体,边表示个体间的相互作用[1]。个体间相互作用所形成的功能模块对应复杂网络中的社区结构,社区内节点间通常存在特殊的连接模式,利用这些特殊连接模式进行社区结构发现是目前的研究热点之一。大量社区发现算法已被广泛应用到商品推荐、社会关系分析、疾病网络分析等诸多领域[1-3]。
早期的社区发现算法侧重于进行非重叠社区发现,即任意两个聚类间不存在公共节点。实际上,重叠社区在真实网络社区分布中普遍存在,如在线社交网络不同社交群体间可能存在相同的用户[4]、科研协作网络中的不同研究群体可能存在交叉合作的科学家[5]、复杂生物网络中的不同生物过程可能包含相同的生物要素[6]。重叠社区发现算法根据网络中社区内节点间特殊的拓扑连接模式对其中的复杂社区归属关系进行解析。
2005 年 Palla等[7]提出了派系过滤算法CPM,将k-团作为构成社区的主要连接模式进行重叠社区发现。k-团是网络中包含k个节点的完全子图,以稠密子图作为社区典型连接模式,可发现内部连边非常稠密的社区结构。除k-团外,现有工作也提出了极大团、准团等多种稠密子图的定义方式[8]。基于稠密连接模式的社区检测算法通常假设社区内部节点间存在大量连接,这种假设不利于发现实际网络中普遍存在的内部连接不够稠密的社区。此外,由于不同网络连接密度差异较大,度量这些网络中子结构的连接稠密程度耗时较多,无法通过遍历大规模网络中的子结构发现其中的社区。
基于信息传播机制的重叠社区发现COPRA算法[9]假设社区内节点间更容易进行信息传播,因此其基于信息传播影响力最大化原理,根据邻域社区标签信息迭代更新节点的社区归属。由于仅考虑直接邻居对社区标签的影响,COPRA算法可能会产生较多规模偏小的社区。已有工作对其进行改进,包括基于历史标签信息传播算法SLPA[10],基于局部结构的标签传播算法DEMON[11]等。该类算法基于信息在网络上的传播模式进行社区发现,节点更新顺序和标签更新过程存在较大的随机性,因此发现的社区结构通常不稳定;且社区发现结果与网络中影响力大的节点关系密切,这些影响力大的节点对应于网络中存在较多连接的节点。这类算法往往将这些节点及其邻居节点分配到一个巨大社区中[12]。
基于局部核心扩展策略的重叠社区发现算法对网络中局部拓扑结构的连接特征进行解析,首先确定社区代表性强的节点作为社区核心,设计合理的核函数计算网络其他部分与社区核心的相似性,选取相似性高的子结构对社区核心进行扩展,以发现网络中社区结构。该类算法的关键在于社区核心选取及核函数定义。早期的核心扩展策略通常为每个可能的社区选择单个节点作为社区核心进行扩展,也称为“种子扩展”策略。算法LFM[13]在网络中无社区归属的节点中采用随机方式选取种子节点,随着网络规模的增大,种子选取过程中的随机性更容易导致不稳定的社区发现结果。重叠节点一旦被选为种子节点,算法倾向于将两个重叠社区识别为一个社区。算法CFCD[14]选择k核中心性高的节点作为种子,算法LOCD[15]假设不同社区的种子节点具有较高的连接度且不同社区的种子节点相距较远。算法GCE[16]选取网络中k-团作为初始种子进行扩展,在一定程度上提高了算法稳定性。算法LFM和GCE对比社区内外连边比例评价一个社区的显著性,选择可增大社区内外连边差异的节点扩展初始社区;算法LOCD选择可增大社区内部节点间Salton相似性的节点扩展社区;算法CFCD选择可增加社区内节点的k核中心性的节点扩展社区。这些社区扩展方式所定义的社区适应度函数可发现网络中内部连接相对稠密的社区结构,但对大规模网络中内部结构差异较大的不同社区结构识别效率不高。
个性化PageRank的社区扩展算法NISE[17]对采用导电性对种子节点邻域的信息传递能力进行度量,发现社区间信息传播最小化的社区结构。算法Node_Perception[15]在各节点局部邻域子图内利用标签传播算法发现局部社区结构,将连边较多的局部社区合并最终社区发现结果。以上方法在种子节点选择及扩展过程中考虑的节点邻域的连接模式,通过合理的社区扩展过程更好地检测重叠社区。
然而,网络中往往存在一些特定的模体来行使特定功能,这些模体表现为节点子集内特定的连接模式。模体结构体现了网络内节点间连接的高阶特征,一个社区内往往存在一种或少数几种典型的模体结构。利用模体信息对网络功能模块进行分析和挖掘有助于深入理解网络功能和演化机制。本文提出了一种基于局部模体相似性的重叠社区发现算法SLMD,首先统计网络中3-模体和4-模体的分布信息,基于k-WL核计算基于局部模体信息的节点中心性,发现网络中模体相对集中的一些局部拓扑结构作为初始社区种子;根据邻域结构内模体分布的一致性定义了子结构间的相似性,选择相似性较高的子结构对初始社区进行扩展;最后,合并重叠度较大的社区得到最终社区发现结果。
基于网络局部模体分布的高阶信息可以选择相对稳定的社区核心,因此所提算法SLMD具有良好的稳定性;基于模体分布一致性进行社区扩展,算法可以发现网络中内部连接差异较大的社区结构。在7个有真实社区标签、4个无标签的网络上的对比实验表明了所提算法的有效性。
1 背景知识
1.1 基本概念与术语
给定一个包含n个节点的图G=(V,E),其 中 节 点 集 V={v1,v2,…,vn},边 集 E={(vi,vj)|1≤ i≠ j≤ n}。令 A∈ Rn×n为图 G 的相邻矩阵。若边(vi,vj)∈E,则Aij=1,称u和v互为相邻节点。令 Nv={u|(u,v)∈E∧u∈V}表示节点v的相邻节点集合,也称v的直接邻域。记节点vi的度di=|Nvi|,也可以记作di=。对图G'=(V',E'),若V'⊆V,E'⊆E,则G'是G的一个子图,记作G'⊆G。若V'⊆V且边E'={(vi,vj)|vi,vj∈ V'∧(vi,vj)∈ E},则 称 子 图 G'是图G的导出子图,记为G[V'],简记为[V']。顶点子集S(⊆V)的体积为Vol(S)=∑v∈Sdv,表示S中所有节点的度数和。
对两个图 G1=(V1,E1)与 G2=(V2,E2),如果存在双射函数f:V1→V2,且对于V1中的任意 两 个 顶 点 u 和 v,若 (u,v)∈E1当 且 仅 当(f(u),f(v))∈ E2,则图 G1和 G2是同构的,记作G1≅G2。设顶点子集S(⊆V)的导出子图为[S],若图G中与[S]同构的子图出现频率远高于在随机网络中出现的频率,则[S]称作图G的一种模体。模体是网络中一些具有特定结构的小规模子图,刻画了网络内部节点间连接存在的特定模式。
复杂网络中节点通过连接形成不同的团簇行使特定的功能,这些团簇也称为社区,分析网络中的社区结构是复杂网络分析的重要任务之一。对一个图G和它的k个若干节点子集,满足V=C1∪C2…∪Ck,则称 Ω={C1,C2,…,Ck}是 G的一种社区结构,k为社区个数。若对任意的1≤i,j≤k,有 Ci∩Cj=∅,则 称 Ω 是 非 重 叠的;否则Ω为一种重叠社区结构[18]。
节点间连接稠密是社区结构内最常见的连接特征之一,在已有社区发现算法中被广泛使用。然而,除连接相对稠密之外,社区内节点间往往还存在一些特殊的连接模式而形成特定类型的模体。发现网络中具有统计意义的模体信息,并有效利用模体与网络社区结构的关联关系,可以发现网络中连接模式差异较大的社区结构。
1.2 基于种子扩展策略的社区发现算法
早期的社区发现算法往往需要网络的全局结构信息,因此当网络规模急剧增大时,遍历网络全局结构的计算代价过高。而“种子扩展”策略在社区发现过程中不需要对网络全局结构进行遍历,仅需分析节点或子结构的局部邻域内的拓扑特征,因此,基于种子扩展策略的局部社区发现算法可以更有效发现大规模网络或未知全局信息的动态网络中的社区。其中一个关键点是确定候选社区的初始种子,早期的基于种子扩展策略的社区发现算法过程通常首先选择一个中心性较高的节点作为社区种子,再根据一定的相似性度量方法计算其他节点与社区种子的距离或相似性,选择与种子较近(或相似性较高)的节点对社区种子进行扩展,最后对未聚类节点或聚类模糊的节点进行后处理。
在网络规模较小,且社区内部连接稠密的情况下,选择单个节点作为社区种子在实际应用中取得了比较好的效果。然而,当社区中无中心节点时,无法找到合适社区种子进行扩展,则应根据社区内节点间特定的连接模式进行社区发现。GCE算法利用社区中稠密连接所形成的团派连接模式进行社区发现,但不易发现内部不存在完全连接的社区结构。ATCO算法利用社区内三角形连接情况发现社区[19]。
团派和三角形在一定程度上刻画了社区内节点间特殊的连接模式,然而不同网络内有统计意义的模体各不相同,即使同一网络中的不同社区内可能也存在不同的模体。如何有效利用网络中的模体信息及模体结构间的连接方式进行社区发现是本文的重点研究问题。
2 基于局部模体分布相似性的节点中心性度量
本节利用网络中的模体信息及模体结构间的连接方式进行社区发现,首先给出网络模体相邻矩阵,统计网络中节点邻域结构内的模体及模体间连接关系;基于模体分布计算节点间的局部邻域结构的相似性,并给出了基于模体分布的节点中心性度量指标。
2.1 节点k邻域模体分布熵
对v∈V(G),定义Ht(v)表示由其t步闭邻域内所有节点导出的子图,即Ht(v)=[Nt(v)∪{v}]。本节利用邻域内包含3个节点和4个节点的连通模体度量节点邻域模体分布的相似性。节点个数为3或4的连通模体共有8种,如图1所示。k-模体分布Γk:V→R|T|为节点集到|T|维欧氏空间的映射,其中T为模体集合,表示节点的k步邻域内模体分布情况。对节点v∈V(G),,其 中 γi(v)表示节点v的k步邻域内模体Ti的出现次数,本文仅考虑图1所示的8种连通的3-模体和4-模体。
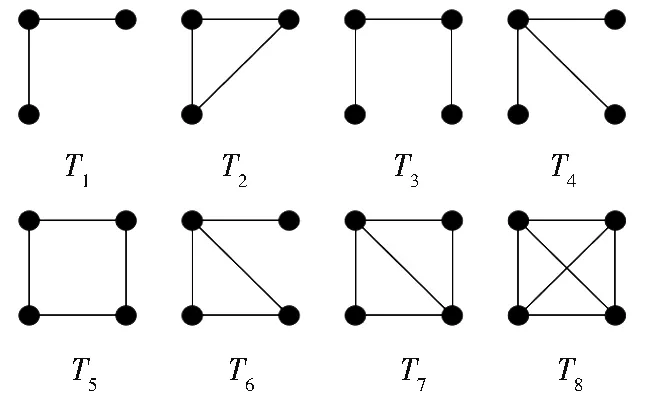
图1 连通的3-模体和4-模体Fig.1 Connected 3-motifs and 4-motifs
计算模体分布Γk(v)的香农熵来度量节点的第k步邻域内模体分布的分散程度,称节点v的模体分布熵,如公式(1)所示。
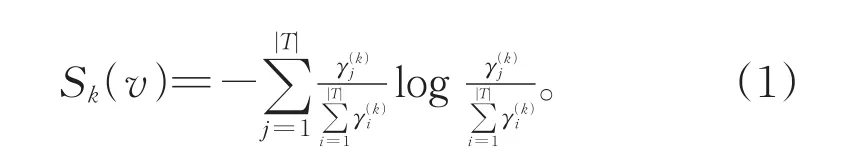
由于度数较低的节点周围通常模体较少,可能出现其模体分布向量为0,或某些分量为0的情形。因此在公式(1)中规定,若Γk(v)为0向 量 ,则 规 定 其 Sk(v)=0;若 Γk(v)的 分 量,则令。节点度数大且模体分布熵越高,说明节点v局部邻域内的模体分布越丰富,可能位于社区中心或者处于社区的重叠部分;否则,若节点度数低或模体分布熵偏低,说明节点v的局部邻域内模体结构比较单一,成为社区中心的可能性较低。
2.2 基于k-WL核的节点特征序列生成
Weisfeiler-Lehman(WL)方法是 Boris等提出的图同构检测方法,将节点的特征信息和结构信息映射相结合,对节点进行重标签,在同一同构轨道的节点被赋予相同标签。本文基于节点v邻域内的3-模体和4-模体分布情况,采用WL核方法对网络节点进行重标签,生成节点特征序列。算法1给出了基于k-WL核的节点特征序列生成方法。

2.3 基于模体分布的社区适应度
社区内节点间连边相对社区间较多,社区结构的显著性通常利用社区内节点间的连接稠密程度来衡量,但这无法体现模体结构对社区的影响。社区内的连边往往会形成一些特殊的连接模式以行使特定社区功能,社区内存在某种模体的出现频率会高于随机连接情况。基于此,用社区内某种模体的显著性定义社区适应度,如公式(2)所示。
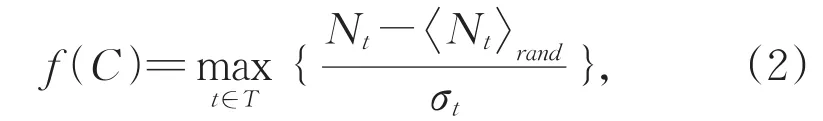
其中,Nt表示C中模体t的出现次数,和σt分别表示与C具有相同节点数和边数的随机零模型中模体t的出现次数和方差。
3 基于局部模体分布相似性的社区发现算法
基于以上提出的基于邻域模体分布的度量指标及节点特征表示,本节给出基于局部模体分布相似性的重叠社区发现算法(overlapping community detection method according to Similarity of Local Motifs Distribution,SLMD),算法基于中心扩展策略进行社区发现,首先根据模体分布情况确定初始社区核心,再利用模体分布相似性的对初始社区核心进行扩展,最终将存在较多连边的社区进行合并。
3.1 初始社区核心确定
对图G=(V,E)中的每个顶点v,首先计算节点v的k步邻域内各类3-模体和4-模体的出现频次,再根据公式(1)计算节点v的k步邻域内模体分布熵。一个节点度越大且模体分布熵越高,成为社区中心的可能性也偏大。因此本节结合节点度与模体分布熵定义节点的社区中心性,如公式(3)所示。
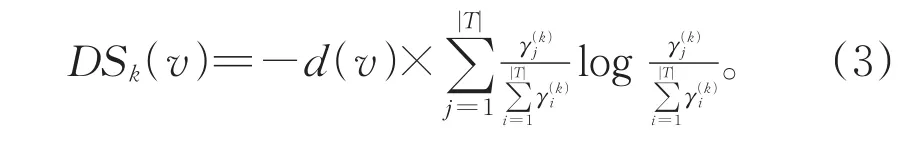
将G中节点按照中心性非递增排列,假设排序后结点编号为 V={v1,v2,…,vn}。 对于1≤i<j≤ n,有 DSk(vi)≥ DSk(vj)。选择中心性高于平均值的节点作为初始社区中心节点集,其中为图G中节点中心性平均值。首先获取中心性高于平均值的节点集导出子图的连通分支,每个连通分支作为一个社区的初始中心节点集。将连通分支作为初始中心节点集,可以避免两个不同社区中心节点相邻而导致的过大社区,同时,可以无需用户预先确定社区个数,导出子图的连通分支个数即为社区个数。初始社区中心节点选择过程如算法2所示。

3.2 社区扩展阶段
在社区扩展阶段,利用第2.2节定义的基于k-WL的节点特征分布序列,比较当前节点与初始社区中心节点间的距离,将其分配至距离最近的社区。由于每个社区可能有多个初始中心节点,因此用节点与社区中心节点集的平均距离作为社区分配的依据。采用相对熵计算节点u和v间节点特征分布的相似性,如公式(4)所示。
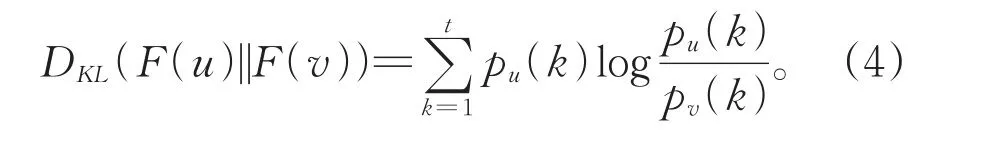
为确保两点间相似性计算的对称性,本文采用公式(5)计算节点间相似性。
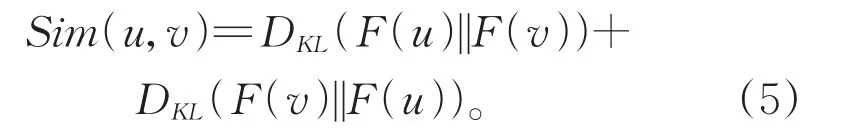
初始中心节点集扩展为社区的过程如算法3所示。

3.3 合并重叠度高的社区
采用以上步骤进行重叠社区发现,通常会产生很多重叠度较大的社区,导致发现过多社区。因此,算法最终将所发现社区的构成进行比较,若两个社区间的公共节点比例高于设定阈值,则将这两个社区进行合并。合并重叠度较高的社区可以更准确的识别网络中重叠社区。两个社区重叠度的计算如公式(6)所示,其中 CC={C1,…,Ck}为图 G 的一种社区发现结果,Ci和Cj为其中两个不同社区。
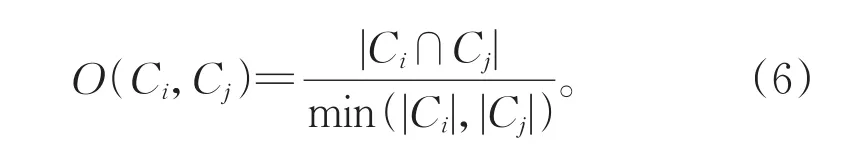
本文中合并重叠度大于0.8的社区。
4 实验结果
为验证所提算法性能,本节将在7个带标签网络和4个无标签网络上,将本文算法SLMD与6个经典重叠社区发现算法SLPA[10]、DEMON[11]、CPM[7]、节 点 感 知 算 法(Node_Perception)[20]、Ego_Networks[21]、Ego_Splitter[21]进行比较实验。表1给出了实验数据集的基本信息。
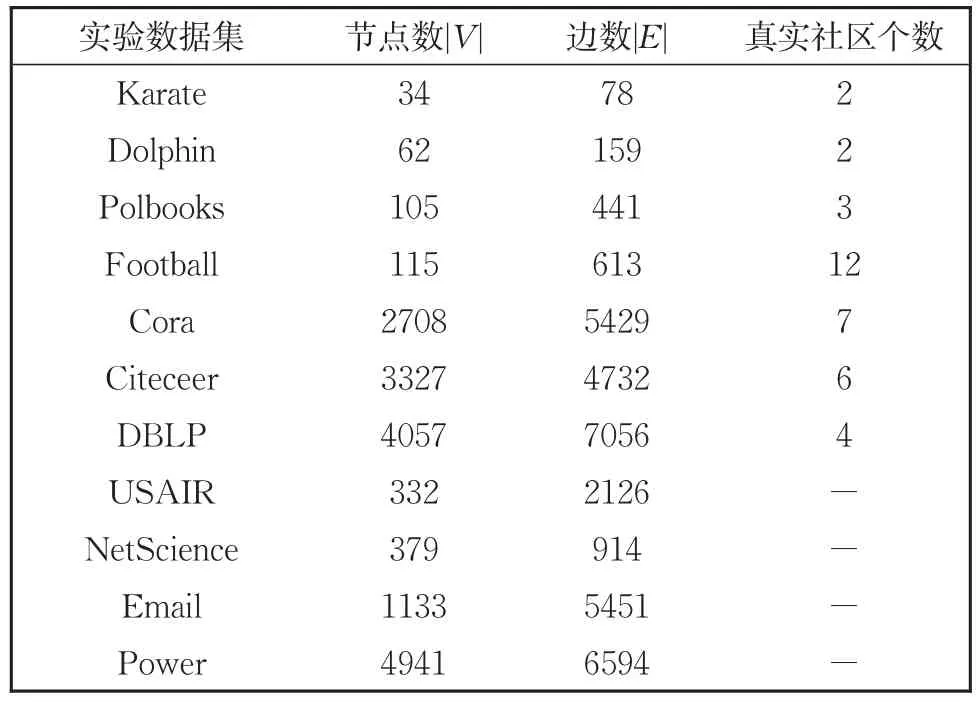
表1 实验数据集信息Table 1 Information of experimental datasets
4.1 评价指标
对带标签网络,本节首先采用由McDaid等[22]提出的重叠标准互信息ONMI指标对算法性能进行比较。假设 Ω ={C1,C2,…,Cm}和O={O1,O2,…,Om'}分别表示两种不同的社区结构,重叠标准互信息通过比较两种社区结构中各社区的重叠程度来衡量其一致性。此外,本节还采用Rossetti等[23]提出的F1分数对无标签网络进行算法性能比较。ONMI和F1分数的取值范围都是[0,1],符合网络真实社区划分结果的ONMI值和F1分数更接近1。
采用文献[24]提出的扩展模块度EQ对无标签网络上的社区发现质量进行评价,如公式(7)所示:

其中,v和w代表网络中任意两个节点;m代表社区个数;Ov表示在所发现包含节点v的社区数;若节点v和w间存在边,则avw=1,否则avw=0。所发现的社区结构越显著,对应的扩展模块度值EQ越接近1。
4.2 带标签网络的社区发现比较结果
表 2 和表 3 分别给出了在 Karate[25]、Dolphin[26]、Football[27]、Polbooks[28]、Cora、Citeceer、DBLP等7个带标签网络上所发现社区的对比实验结果。可以看出,本文算法SLMD在ONMI和F1分数方面明显优于对比算法,传统的重叠社区发现算法通常发现了大量的重叠社区,导致其与真实社区结构相比,ONMI和F1分数性能较低。由于本文算法SLMD在社区扩展过程和合并过程,可以将重叠度较高的社区进行合并,避免产生大量重叠度高的社区,因此在这些网络上表现良好。

表2 带标签网络上社区发现的ONMI比较实验结果Table 2 Comparative results of detected communities at ONMI on labeled networks
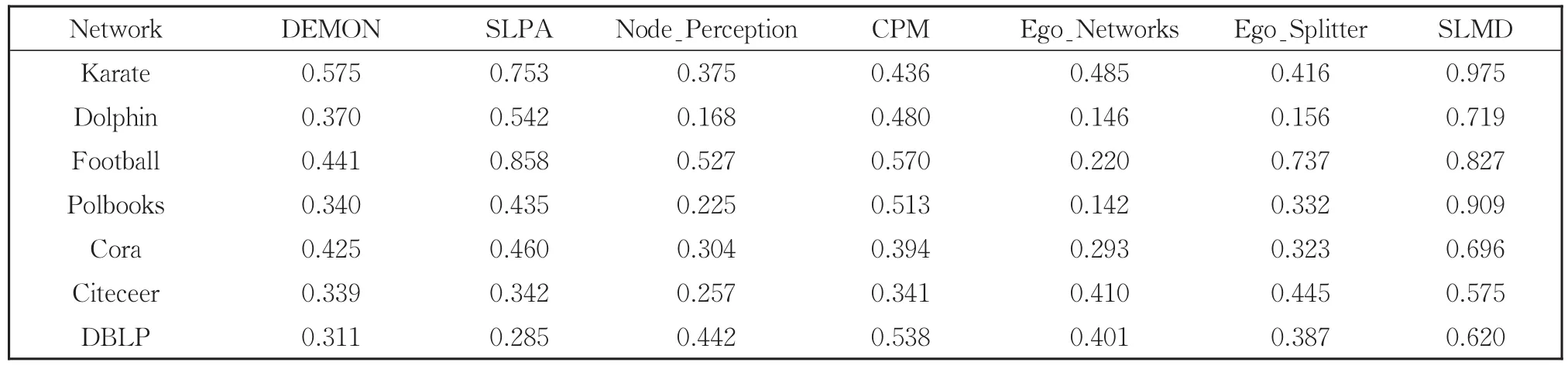
表3 带标签网络上社区发现的F1分数比较实验结果Table 3 Comparative results of detected communities at F1Score on labeled networks
4.3 无标签网络的实验比较结果
表 4 给出了在 NetScience、Email[29]、Usair、Power等4个无标签网络上的对比实验结果。可以看出,在无标签网络上,所提算法SLMD发现的社区结构比较稳定具有较好的重叠模块度。与SLPA算法相比,由于标签传播机制中的随机性较大,导致社区发现结果不稳定。而本文算法利用节点间连接所形成的特殊模体,选择模体相对集中的一些局部拓扑结构作为社区核心,并利用模体分布对社区结构进行评价,这可使算法得到比较稳定的社区结构且具有较高的模块度。

表4 无标签网络上各算法的扩展模块度(EQ)比较Table 4 Comparisons on unlabeled networks on EQ
5 结论
本文基于社区节点间特殊的连接模式信息,提出了一种基于局部模体分布相似性的重叠社区发现算法SLMD,首先统计网络中3-模体和4-模体的分布信息,基于k-WL核计算基于局部模体信息的节点中心性,发现网络中模体相对集中的一些局部拓扑结构作为初始社区种子;根据邻域结构内模体分布的一致性定义了子结构间的相似性,将相似性较高的子结构对初始社区进行扩展;最后,计算所得社区间的重叠度,得到重叠度不超过0.8的社区作为最终社区发现结果。在11个网络上将所提算法SLMD与6个经典算法的比较实验表明,所提算法SLMD在带标签网络上具有较好的重叠NMI和F1分数,在无标签网络上算法SLMD在重叠模块度上有明显优势,可发现具有特定连接模式的社区结构。

