Shuhan图分类及其应用
吴 伟 才, 刘 俊 吉, 谢 卫 军
( 湖南理工学院 数学学院, 湖南 岳阳 414006 )
0 引 言
图论在数学和数学物理的很多领域,特别是在代数的分类方面有着广泛的应用.复数域上的有限维单李代数和Kac-Moody代数的分类都可以用Dynkin图给出[1-2].在文献[3-4]中,Heckenberger 利用广义Dynkin图给出了对角型Nichols代数对应的算术根系的分类.Wang等在文献[5]中利用带参数的交换图给出了秩2的任意域上对角型Nichols代数的分类.在文献[6-7]中,Wang等利用带参数的交换图分类了所有的秩3、4的任意域上对角型的有限维Nichols代数.文献[8]利用树图给出了有限维单李代数的标准Lyndon路.在Kac-Moody代数的研究中,仿射Lie代数分为非扭仿射Lie代数和扭仿射Lie代数两种,其中非扭单边仿射Lie代数因其对应的广义Cartan矩阵是对称矩阵而有良好的性质.本文证明连通的非扭单边仿射Lie代数对应的Dynkin图恰好是全部的最小点数为1的连通Shuhan图.
1 基本定义
令I={1,2…,n},现在回顾一下图论的基本概念[9].令Γ1是一个非空集合且Γ2⊆{{u,v}|u,v∈Γ1,u≠v}⊆2Γ1,则Γ=(Γ1,Γ2)称为一个图;Γ1称为图Γ的顶点集;Γ2称为图Γ的边集;元素{u,v}∈Γ2称为一条边,写作λu,v.如果G=(G1,G2)是一个图且满足G1⊆Γ1和G2⊆Γ2,则G称为图Γ的子图.如果∅≠H1⊆Γ1且H2={λu,v∈Γ2|u,v∈H1},则H=(H1,H2)是一个子图,称为由图Γ中H1生成的子图.λumum-1…λu3u2λu2u1称为从u1到um的一条路.可以定义Γ1上面的等价关系如下:对任意的u,v∈Γ1,u和v是等价的当且仅当存在一条从u到v的路或者u=v.Γ1的每一个等价类生成的子图都叫做图Γ的连通部分.
Shuhan图是一个满足下列条件的无向图Γ(只有顶点有标记):
(i)存在I到图Γ顶点的双射φ;
(ii)对任意的i∈I,顶点φ(i)上标记为xi,xi∈N,N为正整数集;
(iii)对任意的i≠j∈I,φ(i)和φ(j)之间的边数为λi,j,这里λi,j=λj,i∈{0,1};
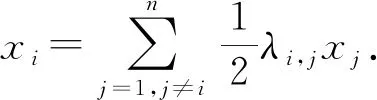
通俗来讲,Shuhan图就是任何一个顶点上面的标记恰好是所有与它相连的顶点上面的标记之和的一半的图.Shuhan图的子图是一个图,但不一定是Shuhan图.
为了表述方便,本文把顶点上面的标记a直接表述成顶点a,标记数记成点数.
2 主要结果
首先给出连通Shuhan图的分类.

(ii)如果a 证明(i)是显然的. 如果没有特殊说明,下文中图的顶点上最少的点数记为a,a∈N. 证明由图Γ的定义,若顶点a与另外的顶点相连,则只能连总数为2a-b的顶点,而2a-b 引理4对于∀l∈N,0 (ii)若给出的图是Shuhan图的连通部分,则点数为la+ra的顶点要与总点数为2ra的顶点相连,由于a最小,则r=0.5且点数为la+0.5a的顶点只能与点数为a的顶点相连,这与引理2矛盾. 证明由Shuhan图的定义,ai=ia1,1≤i≤n,考虑第n个顶点的点数,结论是显然的. 若Γ2l+1是Shuhan图的连通部分,则点数为(2l+1)a的顶点要与总点数为2(l+1)a的顶点相连,且由引理1(i)可知,新连顶点的点数不能少于la+0.5a,又由引理4,只有2种可能: (1)与点数为(l+1)a的另外2个顶点相连,此时新得到点数为(l+1)a的顶点都分别要与另外总点数为a的顶点相连,由于l≥3,与引理1(i)矛盾. (2)与点数为2(l+1)a的另外1个顶点相连,即得到了Γ2(l+1). 若Γ2(l+1)是Shuhan图的连通部分,则点数为2(l+1)a的顶点要与另外总点数为(2l+3)a的顶点相连,且由引理1(i)可知,新连顶点的点数不能少于(l+1)a,又由引理4,只有2种可能: (3)与点数为(l+1)a和点数为(l+2)a的另外2个顶点相连,由引理1(ii)可知,此时新得到点数为(l+2)a的顶点只能与另外总点数为2a的一个顶点相连,由于l≥3,与引理1(i)矛盾. (4)与点数为(2l+3)a的另外1个顶点相连,即得到Γ2(l+1)+1. 用上面的方法归纳得出,若Γk(k≥7)是Shuhan 图的一部分,则最终可以得到一个单链的Shuhan图,这与引理5矛盾. 定理1连通的Shuhan图是图1中的1个(每种情形都有n+1个顶点). 图1 连通的Shuhan图 (1)与点数为a的另外3个顶点相连; (2)与一个点数为a和一个点数为2a的另外2个顶点相连; (3)与点数为3a的另外1个顶点相连. (22)与一个点数为2a的另外1个顶点相连,新得到点数为2a的顶点要与另外总点数为2a的顶点相连.只有2种可能… (3221)与点数为3a的另外2个顶点相连,而新得到点数为3a的两个顶点分别要与另外总点数为a的两个顶点相连,这与引理1(i)矛盾. 命题1(i)连通Shuhan图Γ连接新的顶点得到的图不是Shuhan图. (ii)若Shuhan图Γ的某个子图也是Shuhan图,则Γ是离散的. 证明(i)图Γ中连接新的顶点的点数一定不满足Shuhan图的条件. (ii)由(i)可得. 本文研究了Shuhan图的分类与应用,得到了5种类型的连通Shuhan图,研究结果在矩阵论和Kac-Moody代数以及图论领域中都有广泛的应用.对于顶点之间边数大于1的图,即广义Shuhan图,它们的性质和分类也是一个值得深究的问题.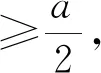



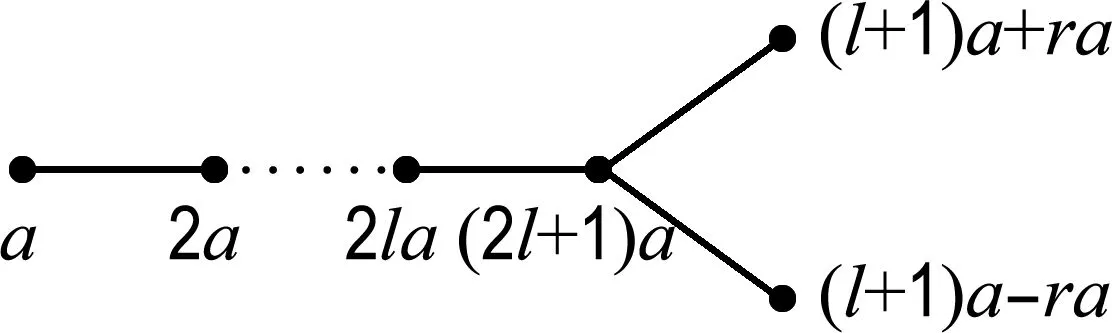
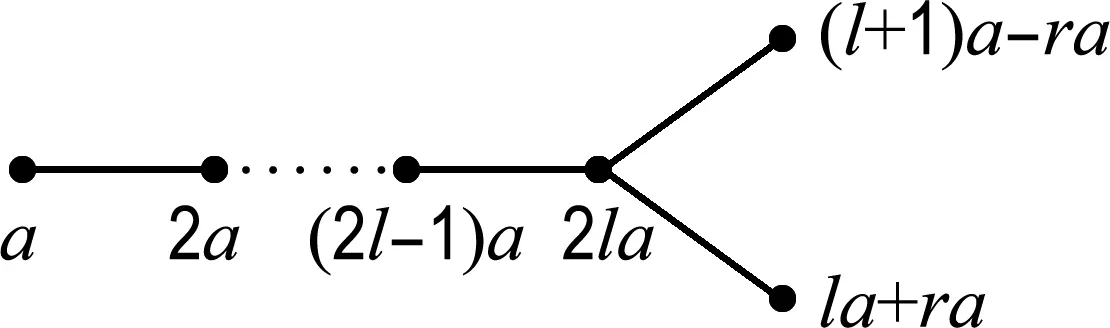
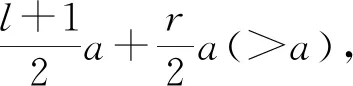



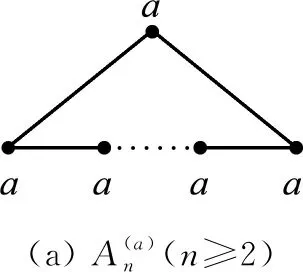

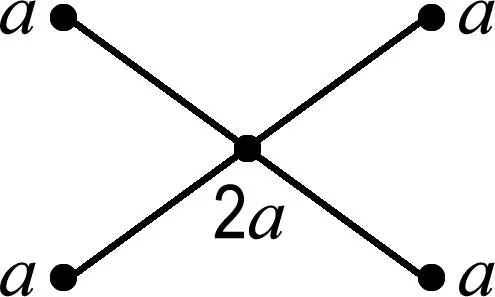


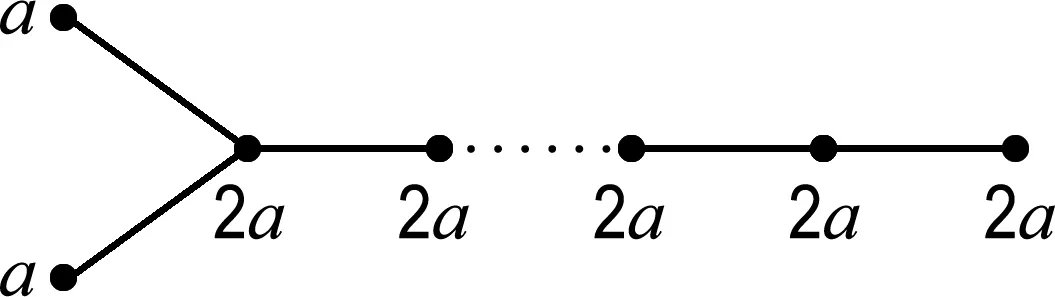
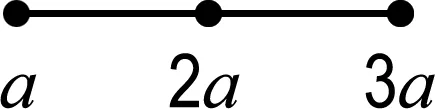
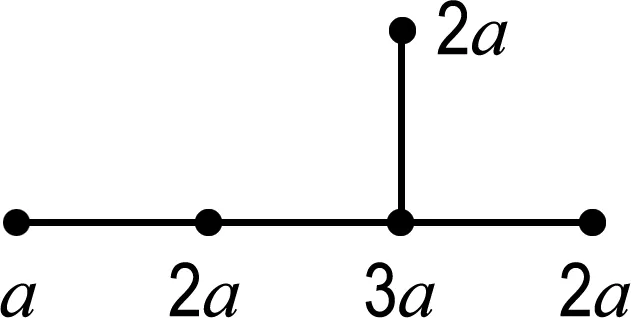

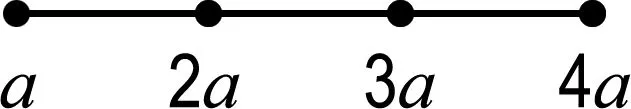
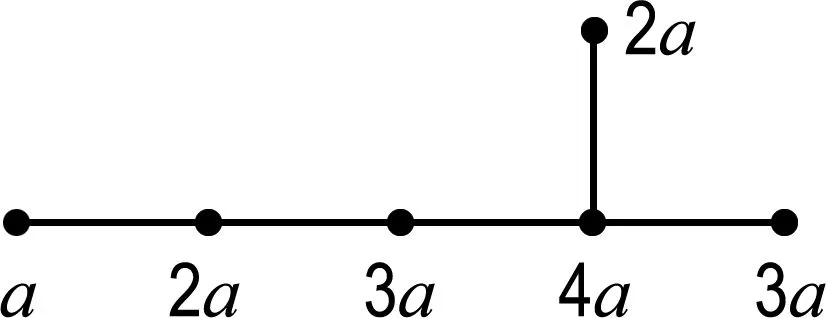
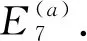
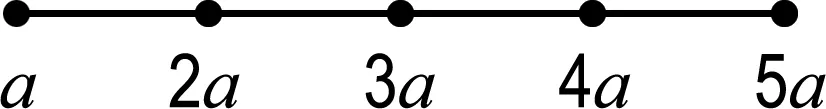


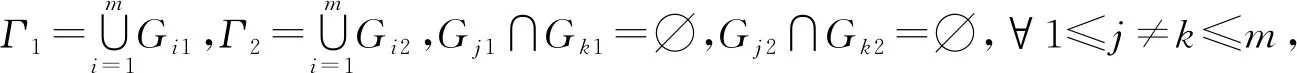
3 结 语

