冲击速度对CFRP加固RC梁动态性能的影响

张亚芳，段莉斌，卢娟，霍永杰

广州大学土木工程学院，广东广州 510006

碳纤维增强复合材料（carbon fiber reinforced plastics，CFRP）因轻质、高强和易于施工等优点，在工程结构加固中应用广泛［1-2］．目前，在静荷载下，国内外学者开展了大量CFRP加固钢筋混凝土（reinforced concrete，RC）梁的理论和试验研究，发现不同CFRP加固形式下加固梁的抗弯和抗剪强度均有所提高［3-6］，并提出了相应的强度计算公式［7-8］．亦有学者发现加固梁的受弯破坏主要有CFRP布拉断-剥离和受压区混凝土压碎-CFRP布剥离两种破坏模式［9］，并给出了CFRP受弯剥离承载力的计算方法［10］．在实际工程中，建筑结构往往还会遭受冲击作用，而钢筋和混凝土材料在冲击荷载下具有明显的应变率效应［11］，导致建筑结构的动态力学性能与静载作用下有很大区别，因此，CFRP加固梁的静态理论在冲击作用下并不适用［12-13］．文献［14-16］发现黏贴纤维复合材料可以提高RC梁的抗冲击能力和残余刚度，显著降低梁的挠度，减小梁体损伤．CANTWELL等［17］进行了不同厚度CFRP加固小尺寸梁的冲击试验，发现CFRP黏贴厚度的增加可以使冲击力有一定程度的增大．PHAM等［18］研究发现FRP加固梁的破坏模式由静载下的延性弯曲破坏变为冲击荷载下的脆性剪切破坏，并且冲击作用下FRP的脱黏应变低于静载作用下.目前对冲击作用下CFRP加固RC梁动态性能的研究相对较少，且现有研究主要从表象探讨加固前后梁的性能变化，缺乏对CFRP加固梁的冲击破坏规律和损伤机制的深入认识．鉴于此，本研究对4根CFRP加固的RC梁进行落锤试验，通过分析不同冲击速度下加固梁的破坏模式、裂缝扩展规律、动态时程响应和能量耗散，得到了冲击速度对加固梁动态性能的影响规律，为更深入认识CFRP加固RC梁的抗冲击行为提供了参考.

1 试验概况

1.1 试件设计

试验设计并制作了4根矩形截面RC梁，梁长2000 mm，截面尺寸为150×300 mm，净跨为1750 mm．混凝土强度等级为C40，保护层厚度为20 mm．梁体纵筋均为HRB400级钢筋，梁底部配置2根Φ18 mm钢筋，顶部配置2根Φ10 mm钢筋，箍筋的间距为140 mm，直径为8 mm，强度等级为HPB300.

分别在4根梁的底部跨中位置黏贴1层CFRP布，CFRP的黏贴长度为1000 mm，黏贴宽度为150 mm．CFRP采用南京海拓公司生产的高性能碳纤维增强复合材料，公称厚度为0.167 mm，抗拉强度为3585.6 MPa，弹性模量为230 GPa，伸长率为1.7%．试验研究落锤冲击速度对CFRP加固RC梁抗冲击性能的影响规律，各试件的基本参数见表1.

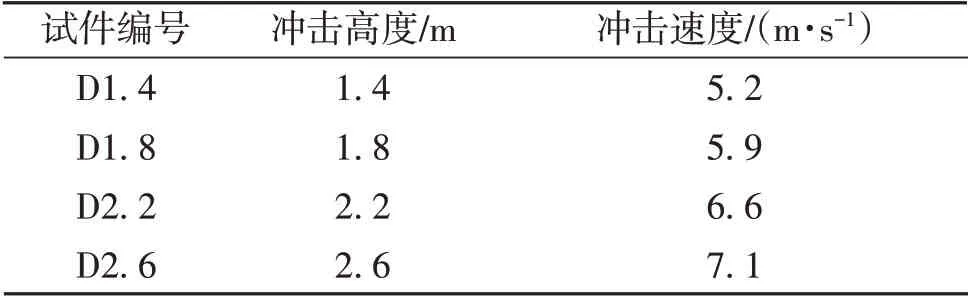
表1 试件参数Table 1 Parameters of Specimens

1.2 试验装置和数据测量

试验装置采用图1所示的高速落锤试验机，锤头为圆柱体，直径为200 mm，落锤质量为575 kg．落锤作用于梁跨中位置，两端支座为铰支座.

图1 落锤试验装置Fig.1(Color online)Drop hammer device.

采用锤头内置的冲击力传感器记录冲击力响应，采用拉杆式位移计记录梁跨中位置的位移响应，数据采样频率设定为50 kHz，采用高速摄影系统记录冲击破坏过程，拍摄帧率选择5000帧/s.

2 试验结果与分析

2.1 冲击破坏模式

4个试件的冲击破坏模式如图2，其中的数值为各试件的裂缝扩展宽度．由图2可见，在冲击作用下，各试件均产生了竖向和斜向两种类型的裂缝，以冲击处为中心形成了明显的楔形损伤区域．文献［19-20］的试验表明，冲击作用下当梁上部未配置纵筋时，支座附近顶部混凝土均产生竖向弯曲裂缝．而本试验在梁上部配置了足够的纵向钢筋，使梁具有抵抗负弯矩作用的能力，因此支座附近梁顶部未产生竖向弯曲裂缝.

试件D1.4跨中附近区域梁底形成3条主要弯曲裂缝，跨中至支座间左右各发展出3条主要斜裂缝，斜裂缝分布较为均匀，两端斜裂缝倾角最大且起始位置靠近支座边缘，靠近跨中位置斜裂缝倾角逐渐减小．随着冲击速度的增大，试件D1.8的跨中附近区域弯曲裂缝增多，跨中至支座间斜裂缝数量和倾角均减小，梁底部混凝土出现碎裂并掉落．试件D2.2出现以剪切破坏为主的破坏模式，跨中至支座间左右仅各发展出一条斜裂缝，跨中附近区域裂缝开展密集，形成宽度较大的主斜裂缝．试件D2.6的破坏最为严重，跨中区域顶部混凝土被压碎的范围最大，梁身产生较多杂乱的次生裂缝，底部混凝土被横向裂缝切断并从梁底掉落，两端斜裂缝起始位置远离支座边缘，整体裂缝分布向跨中区域聚拢.

由图2可知，试件D1.4、D1.8、D2.2和D2.6的跨中区域主弯曲裂缝宽度依次为4.05、5.81、4.61和3.03 mm，跨中区域主斜裂缝宽度依次为1.52、3.78和6.02 mm（D2.6裂缝宽度过大超出测量范围）．可见，随着冲击速度的增加，各试件的跨中区域主弯曲裂缝宽度呈现先增大后减小的趋势，跨中区域主斜裂缝宽度则一直增大．该现象表明，随着冲击速度的增加，加固梁的主要破坏截面由跨中竖向截面逐渐向跨中两侧斜截面转移，即加固梁的破坏模式由以弯曲破坏为主向以剪切破坏为主转变．本研究加固梁的破坏规律与文献［21-22］中的试验结果是一致的.

图2 不同试件的破坏模式（图中数值为裂缝宽度，单位：mm）（a）D1.4；（b）D1.8；（c）D2.2；（d）D2.6Fig.2(Color online)Failure patterns of(a)D1.4,(b)D1.8,(c)D2.2,and(d)D2.6.The value in the figure is the width of the corresponding crack with unit mm.

4个试件中的CFRP均发生如图3（a）所示的剥离破坏．落锤冲击开始后，梁底部CFRP并未第一时间剥离，而是随着梁身裂缝的发展和挠度的增大，梁底部混凝土开裂并向外凸起导致CFRP剥离．由于混凝土为非均质材料，导致梁底左右两侧混凝土的开裂程度不同，因此CFRP的剥离在梁底一侧优先发生．试验完成后对剥离下来的CFRP进行观察，如图3（b），发现CFRP上黏有从梁底剥离下来的大块混凝土以及少量碎屑，说明CFRP与RC梁之间具有良好的黏接效果.

图3 CFRP的破坏模式（a）CFRP从梁底一侧剥离；（b）混凝土骨料剥离Fig.3(Color online)Failure patterns of CFRP.(a)Stripped from the bottom side of the beam and(b)the stripped concrete aggregate.

2.2 冲击力和跨中位移时程曲线

图4 （a）为4个试件的冲击力时程曲线．为了便于观察峰值冲击力的变化规律，放大0～3.0 ms内的冲击力时程曲线，如图4（b）．从图4可见，随着冲击速度的增大，4个试件的冲击力依次在1.40、1.16、0.86和0.60 ms达到峰值，然后冲击力迅速下降至0，形成第1个呈倒三角形的主波形，4个试件的第1个波形持续时间均为1.5 ms左右．文献［20］发现，RC梁在冲击作用下的第1个波形持续时间与冲击速度无关，这与本研究试验结果吻合，说明黏贴CFRP不会改变梁的冲击力变化规律．之后冲击力迅速达到第2个峰值，经过多次循环震荡逐步降低至0．整个冲击力响应过程的持续时间为25～35 ms.

图4 不同试件的（a）冲击力时程曲线及（b）0～3.0 ms内的冲击力时程曲线Fig.4(Color online)(a)Time history curves of impact force and(b)time history curves of impact force from 0 to 3.0 ms of different specimens.

图5 为4个试件峰值冲击力与冲击速度的关系曲线．由图5可知，试件D1.4、D1.8、D2.2和D2.6的峰值冲击力依次为610.2、701.5、846.5和1022.1 kN，冲击力的大小受冲击速度的影响显著．对峰值冲击力进行拟合发现，随着冲击速度的增大，峰值冲击力近似呈线性增长，相较于前一个试件，后一个试件的增长幅度依次为15.0%、20.7%和20.7%.

图5 不同试件峰值冲击力与冲击速度关系Fig.5 Relation between peak impact force and impact velocity of different specimens.Solid diamonds are experimental data and solid line is the fitting line.

图6为4个试件的位移时程曲线．由图6可知，试件D1.4、D1.8、D2.2和D2.6的跨中位移峰值依次为43.3、49.6、60.9和69.6 mm，跨中残余位移依次为28.6、39.8、49.9和58.4 mm．结合图4和图6分析可知，位移响应相对于冲击力响应具有滞后性．在冲击初期OA段（0＜t≤3.5 ms），冲击力主要位于第1个波形阶段，此时跨中位移呈线性增长，并且4个试件的增长曲线几乎重合．在AB段（3.5＜t≤20.0 ms），冲击力进入第2个波形阶段．由于梁自身变形恢复所产生的力逐渐大于冲击力，使梁的变形速度降低，从而使位移曲线由线性向非线性转变．随后冲击力开始进入平稳震荡阶段，在此阶段，冲击速度越大，位移增长速度越快，各试件的位移曲线开始产生分离．在BC段（20.0＜t≤35.0 ms），冲击力下降，位移曲线达到最大值，此时试件的变形在自身刚度的作用下有所回弹，位移曲线开始下降．至t=35.0 ms以后，冲击力作用结束，位移曲线开始保持稳定．由此可见，整个冲击过程中，跨中位移经历了线性增长、非线性增长、回弹和保持平稳4个阶段.

图6 不同试件的位移时程曲线Fig.6(Color online)Time history curves of displacement of different specimens.

图7 为4个试件的跨中峰值位移与冲击速度关系拟合曲线．由图7可知，各试件的跨中峰值位移与冲击速度呈线性关系，这与许斌等［23］试验中得出的曲线变化关系一致.

图7 不同试件的跨中峰值位移与冲击速度关系Fig.7 Relation between mid-span peak displacement and impact velocity of different specimens.Solid diamonds are experimental data and solid line is the fitting line.

除峰值位移和残余位移外，加固梁冲击后的变形恢复能力也是评价其抗冲击性能的重要标准．挠度恢复率Q指梁在变形后恢复的位移与最大位移的比值［24］，可作为加固梁变形恢复能力的重要评价指标．Q越大，代表加固梁冲击后的变形恢复能力越强，

其中，Dresidual为残余位移；Dmax为峰值位移.

通过计算可知，试件D1.4、D1.8、D2.2和D2.6的挠度恢复率依次为34.0%、19.7%、18.1%和16.1%，可见，冲击速度的增加将会导致加固梁的变形恢复能力下降.

2.3 能量耗散

静荷载作用下，施加外力所产生的能量绝大部分被梁体变形所耗散．冲击作用下，初始动能（E）有一部分通过梁体损伤、开裂和变形耗散，这部分能量称为梁的能量耗散（Ea），另一部分以碰撞产生的动能、热能等形式耗散．王路明等［25］指出Ea可以通过对冲击力-跨中位移曲线进行积分得到．对本试验得到的冲击力-跨中位移曲线积分，并计算耗能能力Ea/E，计算结果如图8.

从图8可见，试件D1.4、D1.8、D2.2和D2.6的能量耗散依次为4840、7523、9704和11464 J，耗能能力依次为61.4%、74.2%、78.3%和78.4%，均随初始动能E的增加而增大．耗能能力可以视为评价梁体损伤程度的有效指标，当初始动能相同时，耗能能力越大，梁的变形开裂损伤越严重．试件D1.4的耗能能力为61.4%，说明在此工况下，约2/5的冲击能量被梁以变形恢复等形式转化成动能或其他形式的能量而消耗．相较于D1.4，试件D1.8的耗能能力增加了12.8%，表明随着初始动能的增加，造成梁体损伤的能量占比增大．试件D2.2和D2.6的耗能能力增长分别为4.1%和0.1%，增长幅度愈发减小．上述现象表明，冲击作用下梁体耗能能力的增长是非线性的，初始动能越大，耗能能力增长越缓慢，并最终趋向于一个特定值，即初始动能无法全部由梁体损伤耗散.

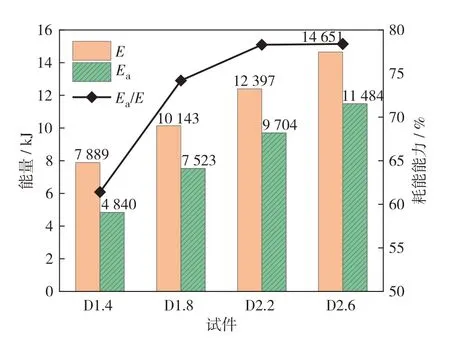
图8 各试件的能量耗散及耗能能力Fig.8(Color online)Energy dissipation,initial kinetic energy(left axis)and energy consumption capacity(right axis)of different specimens.

4 结论

对CFRP加固RC梁进行落锤试验研究，通过分析不同冲击速度下梁的破坏模式、裂缝扩展规律、动态时程响应和能量耗散，可知：

1）随着冲击速度的增加，加固梁的跨中主弯曲裂缝宽度先增大后减小，主斜裂缝宽度则一直增大，整体裂缝分布向跨中区域聚拢，破坏模式由以弯曲破坏为主向以剪切破坏为主转变.

2）在冲击荷载作用下，加固梁的冲击力峰值大小随冲击速度的增加呈线性增长趋势；不同冲击速度下冲击力时程曲线的第1个波形持续时间均为1.5 ms左右，不受冲击速度的影响.

3）整个冲击过程中，跨中位移的发展经历了线性增长、非线性增长、回弹和平稳发展阶段；初始冲击速度越大，加固梁的变形恢复能力越小.

4）随着冲击速度的增加，加固梁的耗能能力呈非线性增长，冲击速度越大，耗能能力增长越缓慢.