基于MPC的无人驾驶车辆轨迹跟踪算法
崔 振,翟陆阳,赵志强
基于MPC的无人驾驶车辆轨迹跟踪算法
崔 振,翟陆阳,赵志强
(徐州徐工汽车制造有限公司 技术中心,江苏 徐州 221000)
基于三自由度车辆运动学模型,为前轮转向的无人驾驶车辆设计了一种轨迹跟踪控制算法,建立了车辆轨迹跟踪状态方程,采用模型预测控制算法,通过滚动优化和反馈校正对无人驾驶车辆实现了最优控制。为了验证运动学模型和该算法的有效性,对运动学模型进行仿真分析,并建立Carsim-Simulink联合仿真平台,分别对直线轨迹和圆形轨迹进行仿真实验。仿真结果表明,该运动学模型和算法能够有效进行无人驾驶的轨迹跟踪。
无人驾驶车辆;运动学模型;模型预测控制;轨迹跟踪;滚动优化;反馈校正;Carsim- Simulink联合仿真平台
随着人们对汽车要求的不断提高,智能化、网联化成为目前汽车发展的重要方向,代表未来的智能网联汽车能够提高驾驶安全性和避免交通拥堵。
轨迹跟踪控制是无人驾驶研究领域的关键技术之一,控制算法主要包括纯跟踪算法PID(Pro- portion, Integration, Differentiation)控制、线性二次型调节器(Linear Quadratic Regulator, LQR)、模型预测控制(Model Predictive Control, MPC)等。纯跟踪算法因为简单易用,已经用于无人驾驶车辆多年[1],但其前视距离的最优值难以获得。早期的学者在传统PID的基础上做了改进[2-3],改进的PID控制器虽然可以较好地控制车辆跟踪期望轨迹,但其控制参数的获取需要通过大量实验进行修正,而且不能实现最优控制。LQR通过将非线性控制系统线性化,并利用该线性模型求解LQR问题得到最优解[4],但LQR无法处理多约束问题,限制了其使用。因此,本文基于模型预测控制算法,对无人驾驶车辆在给定轨迹情况下的循迹效果进行研究。
1 车辆运动学建模
无人驾驶车辆在低速行驶时,轮胎的侧偏角较小,不考虑动力学问题,此时可以使用三自由度的单车模型作为无人驾驶汽车的模型[5]。
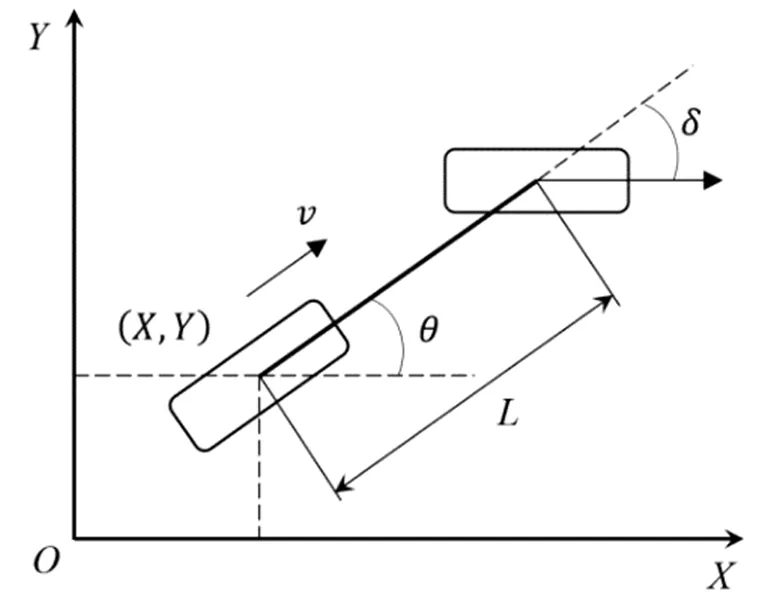
图1 运动学模型
如图1所示,坐标系--为固定在地面的惯性坐标系,(,)为车辆后轴中心坐标,为前轮转角;为横摆角;为车辆后轴中心速度;为车辆轴距。
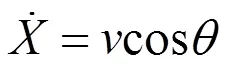
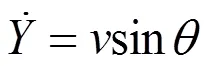
所以可以得到车辆的横摆角速度为
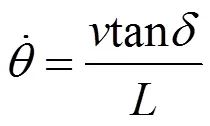
此时车辆的运动学模型为
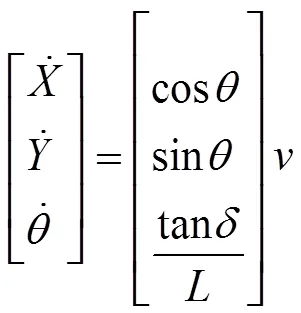
模型预测控制算法具有预测模型、滚动优化和反馈校正几个特征[6],首先建立能够预测系统未来状态的预测模型;其次是建立适当的目标函数,并综合考虑车辆行驶的稳定和迅速的要求,建立合适的约束条件,在每个采样时刻计算出有限时段的最优控制序列,实现系统的滚动优化;最后将最优控制序列中的第一个控制量作为输入,实现反馈校正功能。
1.1 预测模型
由式(4)可知,系统的状态量为=[,,]T,控制量为=[,]T,因此,连续状态方程为
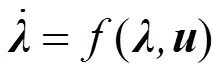
参考轨迹可以表示为
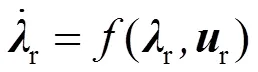
式中,r=[rrr]T,r=[rr]T。
将式(5)在参考轨迹点泰勒展开,只保一阶项并忽略高阶项,得到线性化的无人驾驶车辆误差模型:
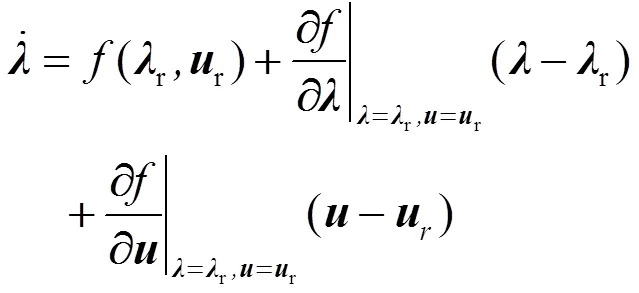
式(7)减去式(6)得
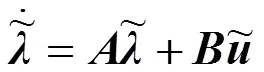
对式(8)进行离散化,得到离散形式的状态空间表达式:
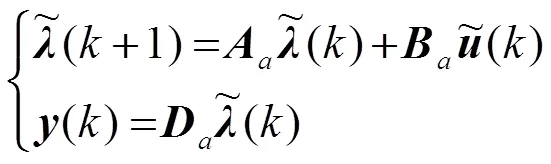
在控制器设计过程中,为防止系统的控制量发生突变,对式(9)做如下转换,将其中的控制量转化为控制增量形式:
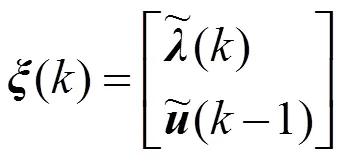
得到一个新的状态空间表达式:
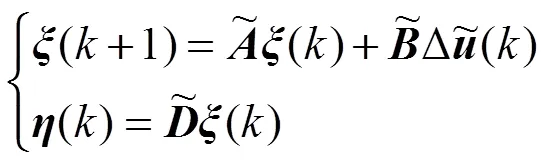
经过推导,得到系统的预测输出表达式:
=()+Δ(12)
由此,可以通过当前的状态量()和控制增量Δ,预测系统未来的状态变量和输出变量。
1.2 目标函数
系统的控制增量无法直接测量得到,因此,需要建立优化目标函数进行求解,参考文献[7]中的方法使用下面的目标函数:
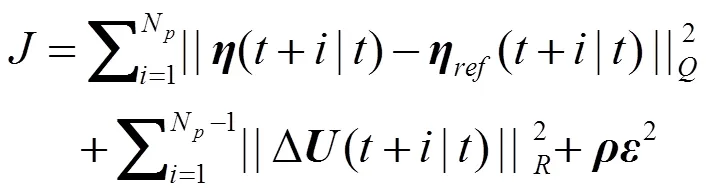
式中,p为系统的预测时域;c为系统的控制时域;实时变化的系统为了避免目标函数无解,设置了松弛因子,同时加入权重系数对目标函数进行软化处理[8]。
1.3 约束条件
在控制过程中,需要满足控制量和控制增量的约束,表达形式为
min(+)≤(+)≤max(+),
=0,1,⋯,c-1
Δmin(+)≤Δ(+)≤Δmax(+),
=0,1,⋯,c-1 (14)
将式(13)中的目标函数转为标准二次型形式,得到如下带有约束条件的公式:
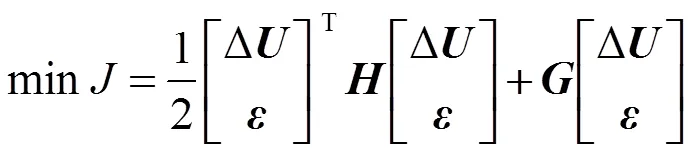
s.t.
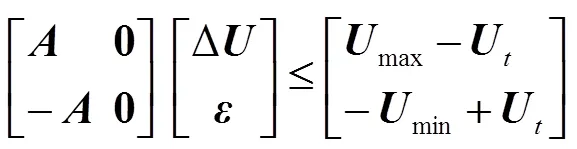
至此,连续系统的模型预测控制问题转化为最优规划问题。
在每个控制周期对式(15)完成最优求解后,得到控制时域内的一系列控制输入增量:
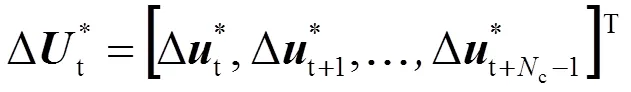
将计算得到的第一个控制增量作用于系统:
()=(-1)+Δt*(17)
系统根据状态信息得到新的控制增量序列,通过对控制过程进行周期性重复,完成对期望轨迹的跟踪。
2 车辆运动学模型验证
为了验证式(4)所得到的运动学模型的有效性,在Simulink里搭建车辆的运动学模型,在相同的速度和前轮转角输入下,与Carsim中的车辆模型输出结果进行比较。
Simulink和Carsim中的运动学模型的速度输入恒为10 m/s,车辆的初始位置和航向角均为0,车辆的前轮转角输入如图2(a)所示,得到的车辆位置和航向角输出如图2(b)和图2(c)所示。
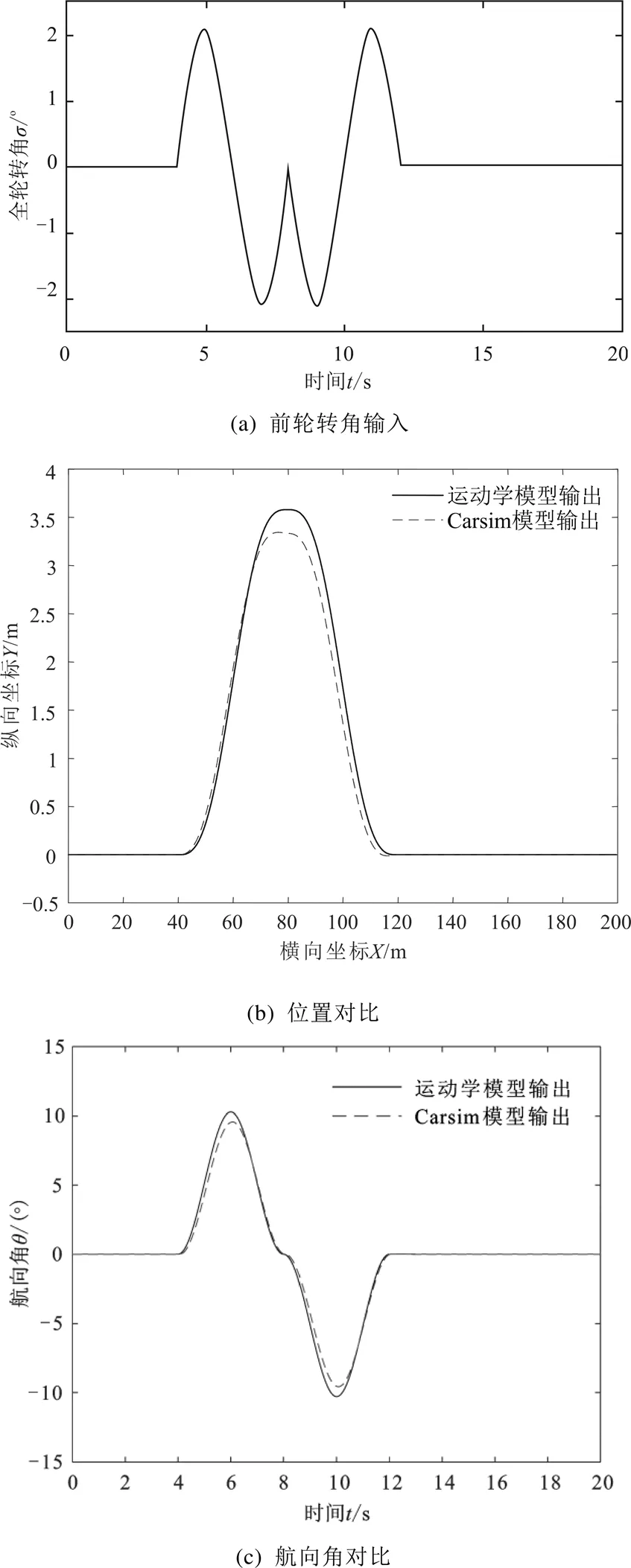
图2 仿真结果
从图2可以看出,在相同的车速和前轮转角输入下,Simulink中搭建的运动学模型输出与Carsim的输出结果十分接近,证明所建立的运动学模型与车辆的实际情况非常接近。
3 MPC算法仿真验证
为了验证模型预测控制算法,在 Carsim和Simulink中进行联合仿真,其过程为在Carsim里对车辆参数进行设置,得到精确的车辆模型,并将其发送到Simulink里,最后根据上文设计的控制器建立Simulink模型。
为了验证设计的跟踪控制器在低车速下对参考轨迹的跟踪能力,选取直线和圆形两种工况对其进行仿真测试。
3.1 直线轨迹跟踪
直线轨迹的参考车速设置为5 m/s和10 m/s,初始位置都为(0,0),航向角为0°,初始时间为0 s,采样时间=0.05 s,参考轨迹为=5的直线。
仿真结果如图3所示,可以看出,在车辆具有初始偏差的初始条件下,以两种不同的速度行驶均能迅速跟踪直线轨迹。
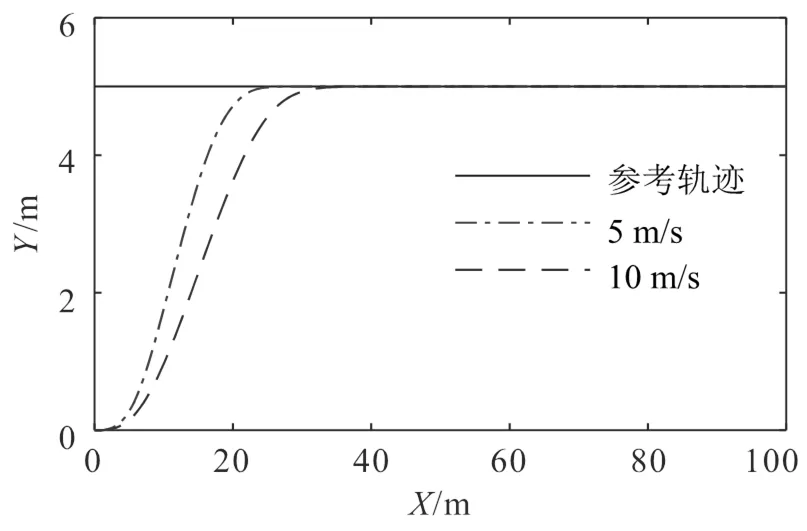
图3 参考轨迹与实际轨迹
3.2 圆形轨迹跟踪
仿真过程依然选取速度分别为5 m/s和10 m/s,车辆的初始前轮转角设置为5.96°,参考轨迹为半径为25 m的圆形,如图4所示。
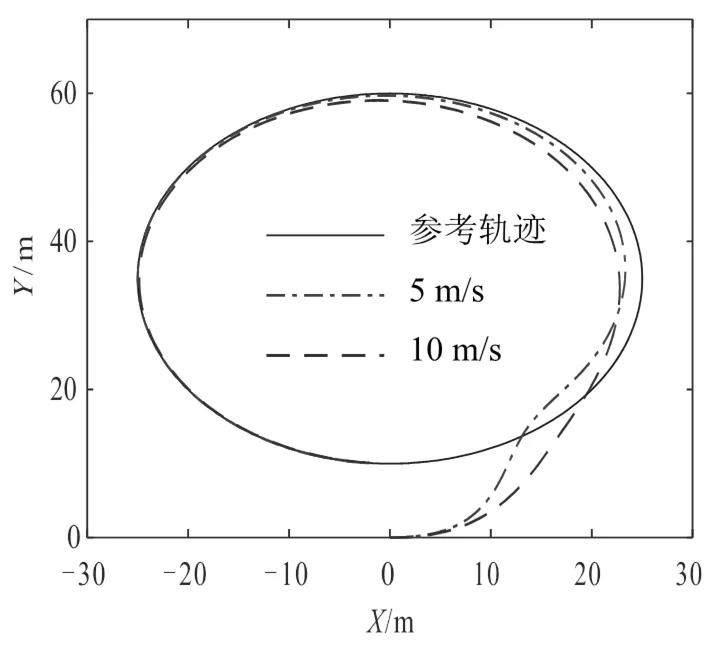
图4 参考轨迹与实际轨迹
从图4可以看出,在具有初始偏差的情况下,两种不同参考速度下,控制器都能够很好地控制车辆对圆形轨迹进行跟踪。
联合仿真结果表明,本文所研究的MPC算法是有效的,在低速时具有良好的鲁棒性和跟踪期望轨迹的能力。
4 结论
本文首先建立了三自由度的车辆运动学模型,并在Carsim和Simulink中对其进行仿真分析,验证了所建立的车辆运动学模型的准确性。对车辆的非线性模型进行线性化和离散化处理,推导出线性时变模型,将设计的控制器在Carsim和Simulink中对直线和圆形轨迹进行仿真验证,结果说明,设计的MPC控制器能够较好地跟踪期望轨迹。仿真结果显示,设计的MPC控制器能够在低速下迅速、稳定地对期望轨迹进行跟踪,对于无人驾驶车辆轨迹跟踪控制的研究具有一定的参考价值。
[1] 吕文杰,马戎,李岁劳,等.基于纯追踪模型的路径跟踪改进算法[J].测控技术,2011,30(7):93-96,100.
[2] 赵熙俊,陈慧岩.智能车辆路径跟踪横向控制方法的研究[J].汽车工程,2011,33(5):382-387.
[3] DONG E,GUO S,LIN X,et al.A Neural Network- based Self-tuning PID Controller of an Autonomous Underwater Vehicle[C]// International Conference on Mechatronics and Automation.Piscataway:IEEE, 2012: 898-903.
[4] 高兴泉,李洪涛,王瑞雪,等.轮式移动机器人的滚动LQR轨迹跟踪控制[J].吉林化工学院学报,2008(2): 38-41.
[5] 龚建伟,姜岩,徐威.无人驾驶车辆模型预测控制[M]. 北京:北京理工大学出版社,2014.
[6] 席裕庚.预测控制[M].北京:国防工业出版社,2013.
[7] KÜHNE F,LAGES W.F,SILVA J M.Model Predivtive Control of a Mobile Robot Using Linearization [J]. Prodeedings of Mechatronics and Robototics,2004(4): 525-530.
[8] 梁忠超,张欢,赵晶,等.基于自适应MPC的无人驾驶车辆轨迹跟踪控制[J].东北大学学报(自然科学版), 2020,41(6):835-840.
Driverless Vehicle Trajectory Tracking Algorithm Based on MPC
CUI Zhen, ZHAI Luyang, ZHAO Zhiqiang
( Technical Center, Xuzhou XCMG Automobile Manufacturing Company Limited, Xuzhou 221000, China )
Based on the kinematics model of three-degree-of-freedom vehicle, a trajectory tracking control algorithm was designed for the driverless vehicle with front-wheel steering, and the vehicle trajectory tracking state equations were established. The model predictive control algorithm was used to achieve optimal control of the driverless vehicle through roll optimization and feedback correction. In order to verify the effectiveness of the kinematics model and the algorithm, the kinematics model was simulated and analyzed, and a Carsim-Simulink co-simulation platform was established to conduct simulation experiments on linear trajectories and circular trajectories respectively. The simulation results showed that the kinematics model and the algorithm can effectively track the trajectory of the driverless vehicle.
Driverless vehicle; Kinematics model; Model predictive control; Trajectory tracking;Roll optimization; Feed back correction; Carsim-Simulink co-simulation platform
U461.1
A
1671-7988(2022)21-43-04
U461.1
A
1671-7988(2022)21-43-04
10.16638/j.cnki.1671-7988.2022.021.008
崔振(1988—),男,工程师,研究方向为智能网联汽车,E-mail: zhen_cui@126.com。

