分数阶不确定Sprott-E混沌系统的自适应滑模同步

王晓东，毛北行

(郑州航空工业管理学院 数学学院,河南 郑州 450015)

混沌源于20世纪60年代，随着分数阶微积分在系统建模中的应用，学者们逐渐开始用分数阶微分方程对混沌系统进行数值建模，并取得了极大成功.随着滑模方法的发展与引入,针对分数阶混沌系统进行滑模控制的研究方法得到了迅猛发展[1-2]:文献[3]针对不确定Victor-Carmen分数阶混沌系统提出了自适应滑模同步的研究方法并取得了相关的研究成果；文献[4]通过引入终端滑模方法研究不确定Duffling分数阶混沌系统的同步；文献[5]提出了两个滑模控制研究方案研究分数阶Newton-Leipnik不确定混沌系统的同步；文献[6]研究超混沌不确定分数阶金融系统的滑模同步；文献[7]研究不确定Bao超混沌分数阶系统的比例积分滑模同步.然而Sprott混系统作为非线性混沌系统的经典代表，引起了广大混沌同步方面相关专家的研究兴趣:文献[8]研究Sprott-I系统的混沌动力学行为；文献[9]研究Sprott混沌系统的分析与控制问题；文献[10]基于延迟反馈研究Sprott-O系统的同步；文献[11]研究Sprott-D系统的H∞同步；文献[12]研究不确定Sprott-C分数阶混沌系统的自适应滑模同步问题；文献[13]研究分数阶Sprott-E系统的动力学分析与投影同步.在上述研究的基础上,论文假设系统具有不确定项和外部扰动的情况下,研究分数阶Sprott-E不确定混沌系统的自适应滑模同步问题,在构造适当的滑模函数、控制器和自适应适应控制律下,获得Sprott-E不确定混沌系统自适应滑模同步的两个结论.

1 主要结果

定义1[14]Caputo分数阶导数定义为

文献[13]中，分数阶Sprott-E混沌系统可描述为

(1)

当a=0.005,q=0.987,x(0)=0,y(0)=0.5,z(0)=0.2,系统吸引子如图1所示.

图1 分数阶系统(1)的吸引子图

以(1)为主系统，设计从系统如下

(2)

其中：Δf(y)代表不确定项，y=[x1,y1,z1]T,d(t)为有界外扰,u(t)为控制器.

定义e1=x1-x,e2=y1-y,e3=z1-z,得到

(3)

假设1|Δf(y)|≤m,|d(t)|≤n,其中未知参数m,n>0.

引理1[14]若x(t)为连续可微的函数，则有

定理1满足假设1下，设计滑模函数s=e3-ke1,k>0,控制器

自适应规则

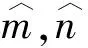
证明当在滑模面上运动时，必满足s=0,由e3-ke1=0,知e3=ke1.

不在滑模面上时，构造

由引理1，求q阶微分得

根据引理2，有|s(t)|2≤2V(0)Eq,1(-2ηktq),从而s(t)→0.

整数阶Sprott-E混沌系统可描述为如下系统(a=0.005)

(4)

整数阶Sprott-E混沌系统的吸引子如图2所示.

图2 整数阶系统(4)的吸引子图

将(4)设计为主系统，从系统如下

(5)

其中：Δf(y)代表不确定项，y=[x1,y1,z1]T,d(t)为有界外扰,u(t)为控制器.

定义e1=x1-x,e2=y1-y,e3=z1-z,得到

(6)

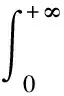
定理2在满足假设1下，设计滑模函数s=e3-ke1,k>0,控制律为

自适应规则为

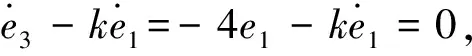
不在滑模面上运动时，构造

求一阶导得

两边积分，有

根据引理3，有s(t)→0.

2 数值仿真

利用MATLAB软件进行数值仿真，系统参数选取如下：Δf(y)=0.5cos(2πz1)d(t)=0.6sin(t),设置初值为x(0)=0,y(0)=0.5,z(0)=0.2.定理1中a=0.005,q=0.987,η=2,k=3.设计s=e3-ke1,k>0,控制律为

定理2中a=0.005，自适应规则为

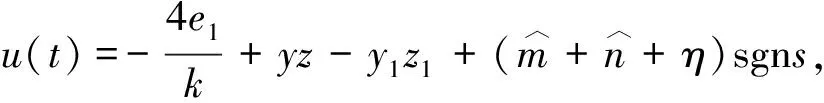
定理1,2中的系统误差如图3,4所示.

图3 定理1中的系统误差

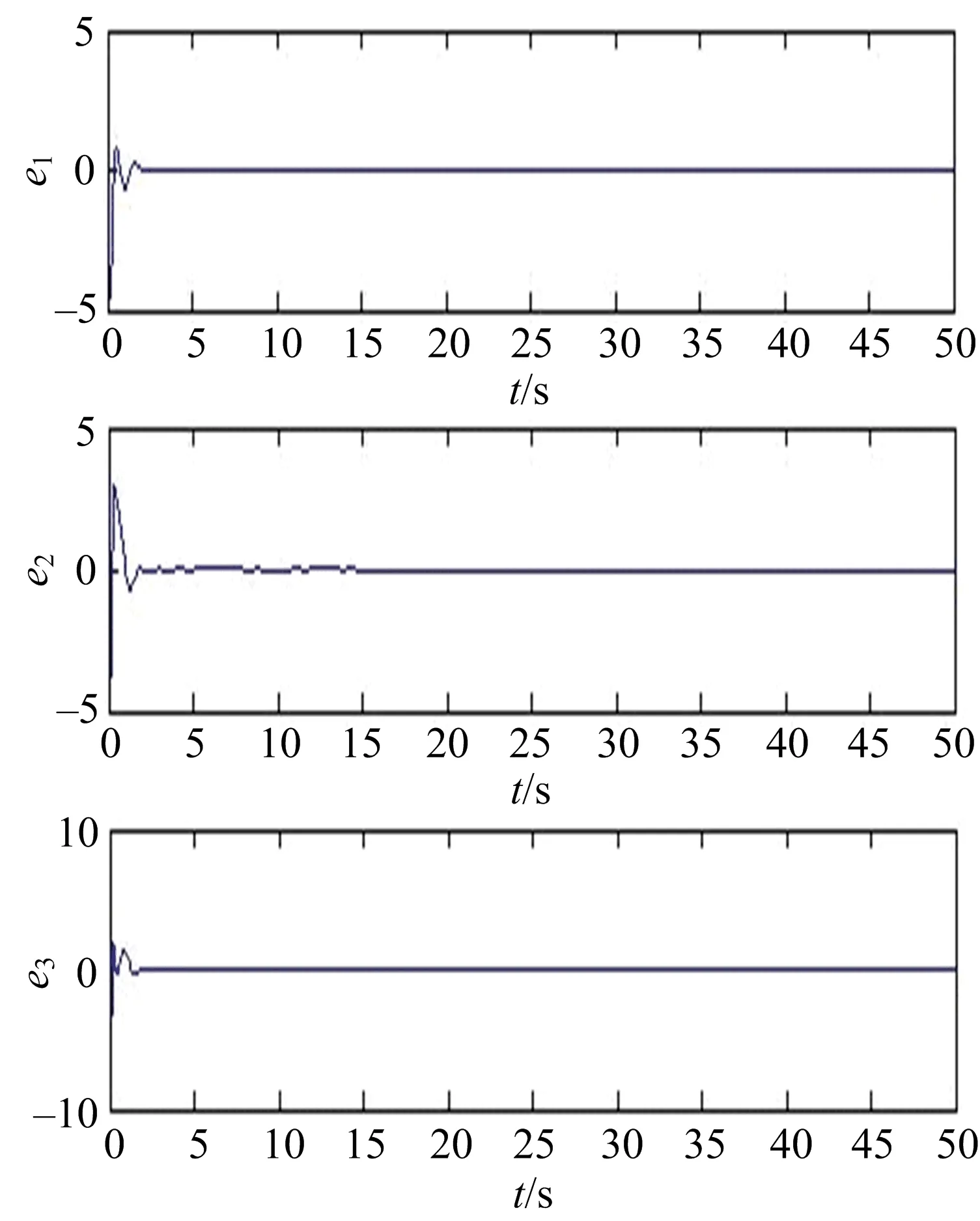
图4 定理2中的系统误差

3 结束语

研究了不确定Sprott-E分数阶具有不确定项和有界外扰下混沌系统的自适应滑模同步问题，通过设计适当的滑模函数，取得了Sprott-E不确定分数阶混沌系统自适应滑模同步的两个研究结果，结论表明Sprott-E不确定混沌系统在适当的假设下能够取得自适应滑模同步，同时将分数阶的相关研究方法和结论推广到了整数阶情形.