可否认加密的数据安全加固技术研究

董 瑞

（青岛农业大学 山东 青岛 250000）

0 引言

民用民生企业日常运营产生的数据通常具有较高的隐私性，若遭到恶意篡改则会造成运行标准或方向的错误，直接导致企业运行生产出现质量问题。例如，一些燃煤电厂等可能排放污染物的企业，若内部控制污染物标准数据遭到篡改，则会直接导致污染物排放超标等问题。对此，为进一步提高企业加密数据的安全性，将对椭圆曲线密码中椭圆曲线数字签名（Elliptic Curve Digital Signature Algorithm，ECDSA）进行研究，通过改进算法的方式对其进行优化，以期达到提高数据加密能力和提高数据加密安全性的目的。

1 网络场景中的典型加密需求

1.1 网络通信中对校验性数据的加密需求

在现阶段企业用网通信中，对校验性数据的应用相对比较广泛，存在的典型校验性数据为：数据完整性、用户鉴权信息、网络设备识别以及系统身份令牌等。对上述数据的加密要求如下：第一，不需要保障信息具有可逆向解密性。在数据加密的思想中，其加密的需求并不单纯防止数据被非法窥探，同时也不是对数据内容本身进行保护，而是出于敏感数据的特殊性，需要对其进行数据隔离，强调数据的不同与不可篡改，以期达到数据保护的目的。第二，对加密效率的要求标准较高[1]。为提高业务访问速度实现最短时间内的认证和比对，需要加密具有较高的效率和简洁的计算方法。

1.2 链路通信数据的加密需求

现阶段使用的链路通信数据加密属于一种保护性较强且严格的网络数据加密。结合已有研究提出的OSI模型能够看出，企业使用的网络通信链路属于底层结构，但其位置处于物理层之上，链路层在加密活动中主要承担对介质的访问，并完成对链路整体的管理。从此加密角度出发，其加密的实质是对链路数据整体的一次加密活动，所需加密要求如下：第一，加解密可逆。链路层通信数据的加密应当能够在每个节点还原数据，并在组织下一次传输时重新加密，因此要求加密具有解密可逆性[2]。第二，具有较高的加密效率的同时还不会占用业务系统的过多资源。因链路层数据的加密涉及很多数据的转发信息，因此链路通信数据加密活动必然会出现繁琐的加密解密和重复加密等活动，需要保障高效加密性能的同时还不占用系统的业务资源，以保障各节点的性能。

2 椭圆曲线数字签名

结合上述常规加密算法分析和已有研究中可知，椭圆曲线标量乘算法中标量乘计的开销较大，同时还会占用较多的系统资源，因此本文将重点对椭圆曲线标量乘算法进行优化，并对椭圆曲线数字签名方案进行研究，以期降低标量乘计的开销，提高数据加密保护的安全程度[3]。

2.1 改进的标量乘算法

假定“E”为椭圆曲线参数，则E（Fp，a，b，G，n，h）。其中，Fp表示素数域；a，b表示椭圆曲线参数；G表示基点；表示基点的阶；h表示协因子。在标量乘算法中，对称三进制因具有较短的表示位和良好的标量乘性能而被广泛使用，但是从该方法的使用中能够看出，该方法存在非零值权重过大的情况，导致在标量乘计算中出现过多的点加运算操作。对此，本文提出针对其异号元素特点，利用相应借位降低其表示存在的非零值权重。若密匙k=841 232，则其对称三进制的表示如下：

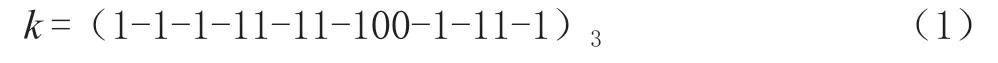
因对称三进制中-1、0、1为基本的元素，因此当基本元素存在相邻的异号元素时，即可借助借位处理的方式将高位转变为0。将k=841 232进行一次借位处理可获得一种新的表示，即：

由此表示能够看出，此表示方法能够将内存占用降低5/13，明显高于式（1）表示的对称三进制。

对算法中标量的对称三进制进行优化从而获得非零值权重的对称三进制，表示具体计算流程如流程1所示。

（3）返回k=（al，al-1，…，a0）3

借助上述方法能够将标量对称三进制中非零值的权重降至最低。

因在对称三进制中基础元素出现的概率均为1/3，所以标量的对称三进制非零值权重为2/3，由此可得出这三种元素的9种不同相邻状态。由不同相邻状态可知，存在相邻异号的组成元素占所有元素出现可能性的2/9，在经过上述算法的处理之后，对称三进制非零值权重将会由原来的2/3降为5/9。

在得到对称三进制非零值权重的表示后，可借助算法流程2进行处理得出标量乘，计算次序为自右向左，具体如下所示。

（3）返回Q

由上述算法流程能够看出，算法主要结合数串中的值进行迭代处理，但是其计算次序若按照从右向左时，其基点的坐标P每次迭代都将会进行一次更新，因而算法流程不能通过预存储操作的方式降低计算量。

结合预存储思想，本文提出一种从左向右降低对称三进制非零值权重的标量乘算法，该方法可借助预存储基点的倍点实现降低标量乘计算量的目的，具体实现方式如流程3所示：

（3）返回Q

上述改进算法流程3中，使用的改进方法为一种借助空间换时间的理念，利用存储基点得出的二倍点计算结果，节省算法流程2中所有二倍点的运算量。对于标量乘算法，若使用仿射坐标的方式进行计算，则会产生较多模逆运算。此计算方法会占用过多的计算资源，因此上述两种改进算法均可以使用雅可比坐标作为仿射坐标的替换，进而除去底层运算过程中存在的模逆运算。

2.2 改进的数字签名算法

在ECDSA算法中标量乘运算被视为最大的计算开销，针对此问题本文已经进行相关的优化研究，但是未能解决ECDSA中模逆运算存在的运算负担[4]。因此，将已改进的椭圆曲线密码数字签名方案解决的ECDSA安全缺陷为基础，在对计算开销问题进行考虑之后，提出一种以密钥隐藏数据摘要为基础的数字签名方案，以期改善ECDSA的安全缺陷问题，并提高数据加密的安全性。

ECDSA签名方程主要由随机数“K”，数据摘要“e”，签名数据“r”，私钥“d”以及签名“s”等五项元素组成。为消除验证端由模逆产生的运算，s必须视为一个单独项进行处理。因接收端验证需要借助计算的数值，所以K同时必须作为一个单独项。而当采用单独的一项时，借助上述分析可知，其能够借助攻击进行消息的更改，并针对信息伪造签名[5]。因签名方程中存在d，将d与e进行组合便可获得组合项d×e，即能够借助组合项的方式对数据摘要进行更改，所以可将签名方程更改为以下形式：

借助上述方法可获得新的ECDSA方案，其生成流程如下所示：

（1）密钥生成

结合椭圆曲线相关参数，随机生成[1，n-1]区间内存在的整数作为用户私钥，然后对进行计算，即：

由此获得(d,Q)。

（2）数字签名的生成

①从[1，n-1]区间中选取随机数k，然后计算kG=（x1,y1）。

②对进行以此取整整合，对r=x1modn进行计算，若r= 0，则返回步骤①。

③运用单向散列函数（SHA256）得到明文m的散列值，即e= SHA256(m)，并对s=（k+r+ed）modn进行计算，若s= 0，则再次返回步骤①。

④将上述操作得到的签名（r，s）附在明文m后进行传输。

（3）数字签名的验证

①首先需要对r和s进行验证，判断是否为0，若为0，则证明验证为不通过。

②将数据和签名进行分离，然后对e=SHA256(m)的散列值进行计算；计算w=（s-r）modn和，若X= 0，则验证不通过。

③令v=x2modn，进行v=r的比较，若二者相等，则验证通过，反之，验证不通过。该算法采用更安全的哈希函数SHA256以生成数据摘要，由此可改变其原始数字签名方案中因SHA1所带来的风险扰动因素，同时还可以借助此方式改写签名方程，使改进算法可以抵御第三方所发起的伪造攻击，提高加密过程与加密结果的安全。

3 算法性能分析

3.1 安全性分析

针对企业产生信息的完整性与不可替换性，在上述算法中使用SHA256作为生成明文的摘要信息方式，在使用SHA256对加密明文进行处理后，所产生的明文信息发生一个容量的变化，便会致使数据摘要发生雪崩效应，因此对数据的加密处理应当确保数据的完整性与不可替换性[6]。加密算法的机密性可视为对私钥的保护能力，因椭圆曲线数据签名的安全性完全依赖于椭圆曲线有限域内存在的离散对数问题，所以即使攻击方截取发送端的公钥，并借助基点和公钥实现私钥的反推，所需的时间是巨大的，因此不具有可行性。同理，若第三方截取签名，并借助签名获取对应的计算结果kG，如果想要继续获取随机数k，则同样需要解决椭圆曲线有限域中的离散对数问题，所以此方法能够保障随机数与私钥的安全性。对上述所提方法的不可伪造性进行验证[7]，因签名方程s=k+r+demodn中存在未知数k和d，若假设原始数据签名为s，攻击者伪造数据为m＇，伪造签名为s＇=k＇+r+d＇e＇modn，接收端接收伪造数据后的进行计算为：

因攻击者无法获得k和d的值，所以只能利用伪造的手段进行迷惑，伪造后的处理为：

由上式可知v=x2modn≠r，证明所提改进密钥隐藏数据摘要的ECDSA方案具备较高的不可伪造性，可被应用于数据的加密中。

3.2 算法性能分析

表1和表2分别汇总I/M=8和I/M=30情况下，仿射坐标系中二进制算法、对称三进制，无存储降低非零值权重的对称三进制标量乘以及存储倍点的降低非零值权重的对称三进制标量乘的计算量分析[8]。

表1 I/M=8 S/M=0.8标量乘计算量分析

表2 I/M=30 S/M=0.8标量乘计算量分析

因在仿射坐标系下标量乘的运算过程需要用到模逆运算，所以一般认为模逆运算属于计算开销最大的一种域运算。而在算法的性能对比过程中，通常需要将其按比例进行转化，以模拟乘运算的形式进行对比分析。通过对比表1和表2中数据可知，当模拟逆运算过程中计算开销越大时，其仿射坐标系下对称三进制标量乘与二进制标量乘的计算量也会随之增大，因此会在一定程度上影响计算效率[9]。

而本文所提改进后的两种标量乘算法，皆使用雅可比坐标的方式消除底层运算中存在的模逆运算，如表3所示。

表3 雅可比坐标下标量乘计算量分析

由上表数据可知，本文通过对对称三进制表示形式的改进，可以有效降低其标量中非零值的权重，从而降低标量乘计算中点加运算的次数，并能够简化计算流程和方法，证明此方法具有较大的便捷性使用性能。

3.3 算法效率分析

由上述分析可知，在加密算法的签名生成中使用一次标量乘的计算和一次模乘的计算，则需要对所提方法的效率即开销进行分析，将本文所提方法与改进的椭圆曲线密码数字签名方案和ECDSA进行对比[10]，并将对比数据汇总于表4所示。

表4 ECDSA计算开销

由上表1中数据可知，本文所提方法与改进的椭圆曲线密码数字签名方案相比可实现不增加计算开销的前提下，提高ECDSA算法的安全性的目标，证明所提方法能够在企业隐私数据加密中以同等的计算量增加数据加密的安全性。

4 结语

综上所述，本文重点对ECDSA方案进行研究，解决ECDSA方案存在标量乘运算所占计算机计算开销较大的问题。同时，在对称三进制的算法基础上提出一种控制非零值权重的算法，由此方法提高加密算法的计算效率，并结合伪造数据标签的问题分析提出一种密钥隐藏数据摘要的数字签名方案，经对比实验可知所提方法可有效提高数字签名算法的安全性与效率。