基于极值搜索算法的多旋翼无人机姿态稳定控制

孙 玉，潘 安

（1苏州农业职业技术学院 江苏 苏州 215008）

（2徐州观音机场 江苏 徐州 221003）

0 引言

多旋翼无人机因其体积小、重量轻等优点成为现阶段应用广泛的一种飞行装置[1]，在目标搜索、地形数据采集等方面均表现出了良好的应用效果[2]。但是也正是因为其存在体积小、重量轻的特点，导致其在飞行过程中极易受到环境中干扰因素的影响[3]。借助其自身具备的相对较强的控制动力[4]，在有效的控制方法下可以有效降低这种干扰因素对多旋翼飞行器姿态的扰动[5]。从该角度分析，选择有效合理的飞行控制方案成了确保无人机稳定高效飞行的关键[6-7]。针对多旋翼无人机姿态控制的研究已经取得了一定的成果，其中，高晶等[8]以四旋翼无人机为研究对象，将RFID技术融入到对其轨迹的跟踪控制中，实现了良好的控制效果，但是在应用范围上存在一定局限性。何志辉等[9]从姿态的角度展开研究，设计了建立在自抗扰模糊参数优化基础上的控制方法，在一定程度上提高了控制的精度，但是仍然存在提升空间。通过上述的分析不难看出，进一步深化对无人机姿态控制的研究是十分必要的[10]。

为此，本文提出基于极值搜索算法的多旋翼无人机姿态稳定控制方法研究，并在仿真环境中分析验证了设计控制方法的效果。借助本文的研究内容，以期为多旋翼无人机领域的相关控制研究和实际应用提供有价值的参考。

1 多旋翼无人机姿态稳定控制方法设计

1.1 基于牛顿-欧拉方程的目标参数获取

实现对多旋翼无人机姿态稳定控制的基础是对其基体运动属性有充分的理解[11]。为此，本文从运动学角度展开分析，获取无人机稳定控制的目标参数。

首先，利用牛顿-欧拉方程对无人机的动力作用机制进行分析[12]。其可以表示为

其中，F表示在运行过程中，无人机受到作用力的总和；m表示为人机自身的总重量，这里的重量既包括无人机机体的固定重量，也包括外带装置所产生的额外重量；a表示在运行阶段无人机的实际加速度参量；L表示在运行过程中，无人机受到作用力矩的总和；e表示无人机自身的转动惯量参数，该数值与无人机的设计直接相关，不受其他因素影响，在具体的计算过程中，以出厂参数为基准。ω表示当无人机的运行状态为转动姿态时，对应的角加速度。多旋翼无人机在运行过程中，获取无人机受到作用力的总和及人机自身的总重量。通过分析无人机机体的固定重量和外带装置所产生的额外重量建立动力作用分析机制，以此得到无人机运行阶段的实际加速度参量。多旋翼无人机在运行过程中，由于受到作用力矩的影响，会改变无人机自身的转动惯量参数。因此，该数值与无人机目标参数具有直接关联，所以在具体的计算过程中，应以转动惯量参数为计算基础，获取无人机运行状态为转动姿态时的对应角加速度。

根据牛顿-欧拉方程结果可知，无论是在直线运行状态下，还是在旋转状态下，无人机的姿态均与对应的角速度直接相关。结合这一特点，充分考虑了不同姿态下的角速度参量[13]。以无人机自身的运行参数为依据，获取参数输出状态与目标状态之间的偏差结果。根据多旋翼无人机在不同方向上的运行分量，计算得出无人机的输出功率。根据无人机横滚角、俯仰角以及偏航角姿态对应的运行角速度参量，获取目标状态之间的偏差。以重力系数和旋翼驱动转矩参量，计算得到无人机驱动力在横滚、俯仰以及偏航方向上对应的惯性动量参数，以此获取无人机运行阶段的升力系数和无人机运行阶段接收到的阻力系数。

通过这样的方式，就可以设定无人机稳定控制的目标参数，将其作为后续状态稳定控制的基础，确保对相关控制参数的设置与无人机实际运行模式具有较高的拟合度。

1.2 基于极值搜索算法的姿态控制

在上述基础上，要实现对无人机的控制就要确保对应的参数信息能够适应实际环境情况对无人机状态的扰动，这就涉及无人机临界状态的分析。针对该问题，本文采用极值搜索算法实现对相关控制参数的计算。

首先，根据无人机稳定控制的目标参数，计算出无人机在当前时刻的运行状态，在不施加额外控制的条件下，计算多旋翼无人机姿态稳定控制最优参数。在此基础上，为了最小化无人机的无功输出，本文设置了代价函数，并将代价函数最小值作为实现基于极值搜索算法的无人机控制器参数整定基础。那么，以代价函数为约束的控制参数计算方法可以表示为：

其中，Δ表示在t到t0期间，无人机模型的实际状态信息与目标状态的偏差，t和t0分别表示目标控制时刻与初始时刻，u表示控制参数，结合无人机的实际控制方式，该参量以对应的设置为准。

通过这样的方式，实现对最优控制参数的计算，但是需要特别注意的是，利用极值搜索算法进行计算的过程中，输出结果的阈值范围要以无人机的可执行参数范围为约束。当输出的结果超出无人机的可执行范围时，表明此时的环境干扰作用已经无法通过自身调节控制的方式得到缓解。此时就需要结合实际情况对具体的飞行方案进行适应性调整，以此确保无人机的安全飞行。

2 仿真测试与分析

在上述基础上，为了进一步分析本文设计控制方法的效果，在MATLAB/Simulink环境中进行了仿真实验测试，考虑到在无人机实际飞行的过程中接收到的干扰具有不稳定的特性，因此本文在测试阶段在测试环境内加入了具有阶跃属性的扰动信号，以此对本文设计控制方法在不同环境下的执行性能进行全面评价。

2.1 仿真测试平台构建

在本文构建的实验平台，使用的飞控装置为PIXHAWK，对应的控制装置硬件为FUTABA-T8FG，为了适应多旋翼无人机的飞行需求，将型号为X-380的机架作为无人机的主体结构。在此基础上，为无人机设置了4个机翼，分别为2对包括正反方向的9045螺旋桨、并且为每个螺旋配置了一个SUNNYSKY-X2212KV980无刷电机以及一个HOBBYING-30A电调。考虑到在实际控制阶段，无论是控制信号的接收还是状态信号的发送，都需要借助对应的数据传输装置，因此，本文为无人机搭载了CUAV RADIO模块，以此满足其通信需求。对于测试旋翼无人机具体参数的设置，具体如表1所示。

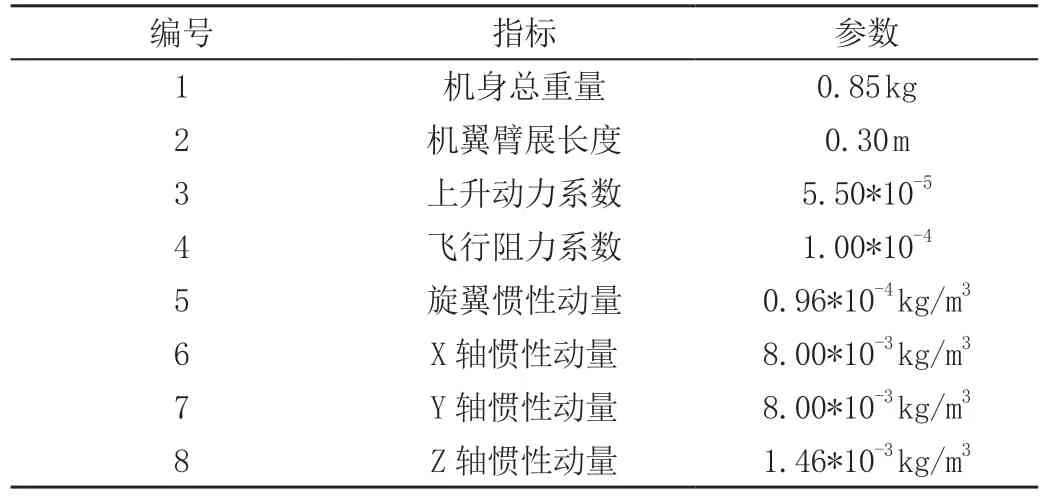
表1 测试无人机机身参数设置

在此基础上，设置无人机在测试前控制参量信息初始值为0，设定姿态角值45°为目标飞行姿态，在飞行10 s后仿真环境内加入阶跃信号，实现对无人机的扰动作用，测试本文方法下无人机姿态的控制结果。

2.2 测试结果与分析

以上述设置为基础，为了能够更加全面地分析本文设计方法的控制效果，在分析阶段，本文分别从横滚轴、俯仰轴以及偏航轴的角度，对无人机姿态的偏差情况进行统计，得到的结果分别如图1、图2和图3所示。

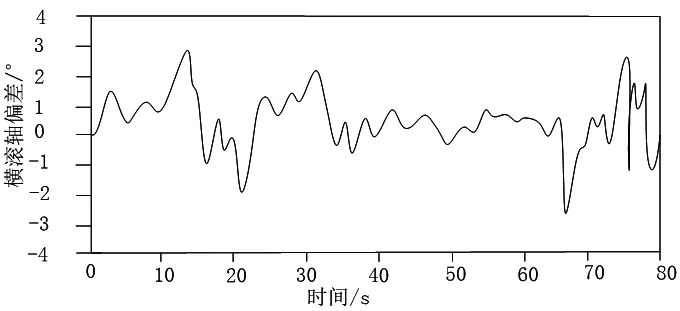
图1 无人机横滚轴偏差情况

通过观察图1可以看出，在无人机飞行期间，横滚轴欧拉角的偏差情况基本稳定在3°以内，在未加入阶跃信号扰动信号的前10 s内，无人机横滚轴欧拉角的偏差幅值为1.5°，在加入阶跃扰动信号后的初始阶段（10～30 s），无人机横滚轴欧拉角的偏差出现了较大幅度的波动，最大值达到了3°。但是在阶跃信号扰动作用中期（30～60 s），无人机横滚轴欧拉角的偏差逐渐恢复稳定，与未加入阶跃扰动信号前10 s内状态基本一致。在阶跃信号扰动作用后期（60～80 s），由于信号的阶跃属性，该阶段的信号扰动强度最大，对应无人机横滚轴欧拉角的偏差幅度再次达到了3°。测试结果表明，在本文设计的控制方法下，可以实现对多旋翼无人机横滚轴姿态的稳定控制。

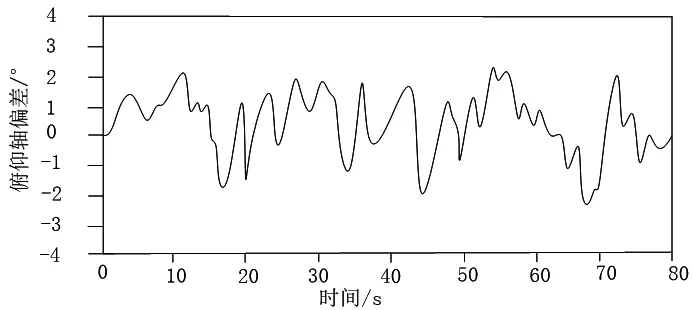
图2 无人机俯仰轴偏差情况

通过观察图2可以看出，在无人机飞行期间，俯仰轴欧拉角的偏差最大值同样为3°。对在未加入阶跃信号扰动信号前10 s内无人机俯仰轴欧拉角的偏差情况进行分析可以看出，其对应的偏差幅值为1.5°。在此基础上对加入阶跃扰动信号后，无人机俯仰轴欧拉角的偏差出现一定程度的波动，与初始阶段的1.5°相比，仅增加了1倍。测试结果表明，在本文设计的控制方法下，可以实现对多旋翼无人机俯仰轴姿态的稳定控制。

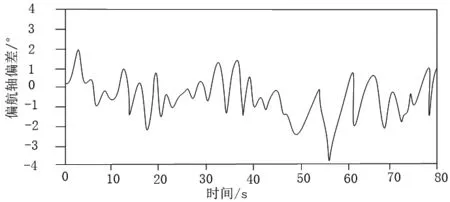
图3 无人机偏航轴误差情况

通过观察图3可以看出，飞行期间无人机偏航轴欧拉角的偏差最大值也仅为4°。对未加入阶跃信号扰动信号前10 s内无人机偏航轴欧拉角偏差情况进行分析，其误差幅值已经达到了2°。在加入阶跃信号扰动信号后的10～50 s时间段内，无人机偏航轴欧拉角的偏差在本文设计控制方法下，并未表现出明显的增加，在阶跃信号扰动作用后的50～60 s时间段内，无人机偏航轴欧拉角的偏差出现了相对较大的波动，与未加入阶跃信号扰动信号前的偏差幅度相比增加了2°，但是在阶跃信号扰动作用后期（60～80 s），无人机偏航轴欧拉角的偏差幅度再次稳定在了2°范围内。这是因为在本文设计的控制方法中，通过极值搜索算法实现了对控制参数的不断寻优，能够结合实际情况对控制强度进行适应性调节。测试结果表明，在本文设计的控制方法下，可以实现对多旋翼无人机偏航轴姿态的稳定控制。

3 结语

综上所述，在无人机的飞行过程中，由于环境等因素的干扰作用，会使得其状态与既定目标发生偏离，这不仅会影响最终的飞行轨迹，同时也会导致飞行任务难以按计划顺利完成。本文提出基于极值搜索算法的多旋翼无人机姿态稳定控制研究，实现了在阶跃信号干扰作用下对无人机横滚轴姿态、俯仰轴姿态以及偏航轴姿态的有效控制，确保对应的欧拉角偏差在允许范围内。借助本文的研究，希望可以为实际的多旋翼无人机应用提供参考价值。