无人车轨迹跟踪控制研究

刘丽霞 刘玮 夏志鹏 郑国宇

盐城工学院汽车工程学院 江苏省盐城市 224051

1 引言

随着科学技术的不断发展，轨迹跟踪的精确性也是学术界和工业界研究的热点。针对无人车轨迹跟踪精度低的问题，国内外学者探索运动控制、结构布置，研究跟踪稳定性增强、跟踪精准性优化的方法[1]。在运动控制方面，基于电驱动转矩和全轮信号反馈响应快的优势，结合了底盘系统多源异构的检测信息，复杂工况下的轨迹跟踪等运动优化是当前无人车控制系统研究的主要方向[2]。此外，四轮转向技术的出现并应用，进一步提高了无人车在运动控制和结构布置方面的优势，成为众多学者研究轨迹跟踪等问题的关键载体。传统汽车的一些机械结构慢慢被四轮转向车辆所取代，汽车的轮毂电机独立控制每一个车轮的角度和扭矩，简化了底盘的结构，并为车辆的路径轨迹跟踪控制提供了合适的条件[3]。这个时候，轨迹跟踪稳定性的难度会因为灵活的转向形式而大大增加，且轨迹跟踪的精度会大大降低。因此，徐兴等[4]在确定权系数时，对权重系数进行了优化，对分布式驱动车辆的转向灵活性与轨迹跟踪的精度有显著的提高作用。

智恒[5]对无人驾驶汽车的轨迹跟踪问题进行了钻研，进一步研究了基于预测模型控制的轨迹跟踪控制算法。张庭芳[6]等为解决四轮主动转向车辆在横向干扰和变道条件下的行驶稳定性问题，提出了一种改进的四轮滑模转向控制算法。而于树友[7]等在三步控制方法的基础上，提出了一种汽车四轮转向主动控制方法。

上述研究成果对车辆在行驶过程中的跟踪稳定性具有较明显的提高作用，但其对车辆路径跟踪精度的研究却缺乏重视，而轨迹跟踪精度是四轮转向车辆适应复杂外界环境和系统误差的先决条件。因此，现如今对于提升轨迹跟踪精度的研究已迫在眉睫。

2 车辆运动特性建模

2.1 动力学建模

如图1所示，首先建立无人车三自由度车辆动力学模型，对车辆进行受力分析。

图1 无人车动力学模型

根据其受力平衡和力矩平衡得到三自由度动力学方程如下：

纵向运动方程

横摆运动方程

式中，IZ是车辆绕Z轴的转动惯量；表示横摆角加速度；表示质心到后轴的距离；表示质心到前轴的距离；d表示车辆的左右轮距。

2.2 运动学建模

本文采用质心为[x，y]T的笛卡儿坐标系，θ为无人车前进方向与X轴夹角，v(t)、w(t)分别为无人车的平移和旋转速度，为无人车等效轮的转速，为无人车等效轮的运动速度，d为车轮直径。考虑无人车需要满足刚体及其运动规律，提出对应的运动方程如下:

3 跟踪控制器的设计

无人车在惯性坐标系中必须从一个给定的初始位置出发，然后通过控制器控制车辆尽量按照规划好的轨迹行驶。

3.1 使用Lyapunov直接法构造全局渐近跟踪控制器

采用Lyapunov直接法来直接判定平衡点是否稳定，然后基于运动学模型，复合跟踪误差的设计依据就是Lyapunov直接法，想要得到参考轨迹的全局渐进跟踪，就需要设计一个全局渐进跟踪器。

结合无人车运动学模型得到：

设计控制律，k为控制参数：

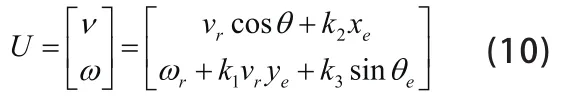
Lyapunov函数变换得到

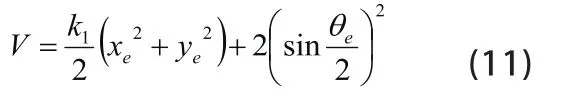
3.2 使用粒子群算法对跟踪误差参数进行整定分析

本文首先采用粒子群算法，接着整定控制参数，为求得控制器参数的大小，先假设搜索到的粒子群属于D维空间，再用c表达出来，其表达式为：

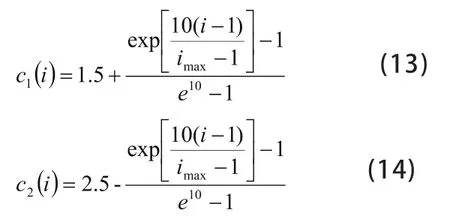
因此结合上述公式自适应粒子群表达式为：

4 基于MATLAB实验仿真

4.1 无人驾驶车辆轨迹跟踪控制仿真

为验证所提出控制策略的准确性和可靠性，在MATLAB/Simulink中对无人车辆进行轨迹跟踪控制仿真。轨迹跟踪仿真实验的基本设定为v=1m/s：坐标原点就是车辆的出发位置，设置的理想纵向速度为，跟踪的那条直线为y=1，30s则被设定为仿真所需要的时间，30ms是设置的采样时间，最终在MATLAB环境下，实现对无人车辆的直线轨迹跟踪过程的仿真。无人车的模型参数见表1：

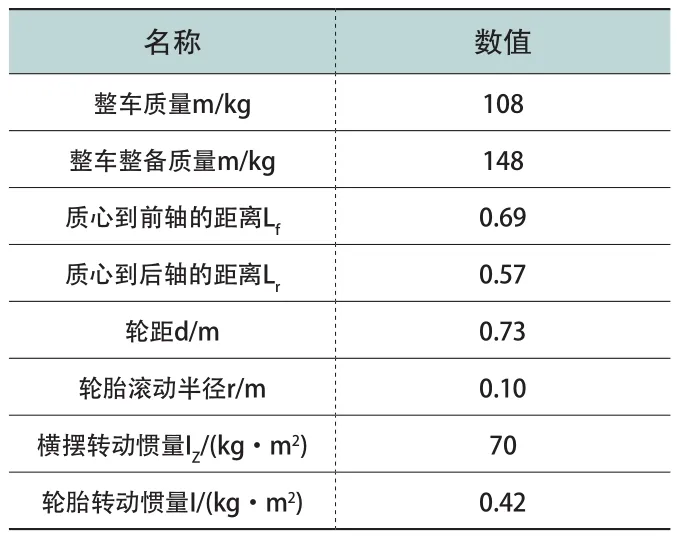
表1 无人车辆参数

利用文中第三部分设计的控制器，在MATLAB中编写相关程序，得到的仿真结果如图2所示。

图2 车辆轨迹跟踪结果

4.2 仿真结果分析

仿真结果如图2所示，期望轨迹是由图中的a曲线来表达的，车辆的位置使用星号曲线b来表示的，曲线c则表示为预测的时间段内车辆所处位置。

根据图2可以看出，经过一定的时间后，在模型预测控制器的作用下，车辆能够迅速跟随期望的轨迹行驶，最终可以稳定地沿着理想的轨迹行驶，达到期望的效果。由于是将线性误差模型用作预测模型，并且车辆位置的解是非线性运动学模型，因此，车辆实际行驶的曲线b与车辆实际输出的位置曲线c不一致。这是因为预测模型通常不是受控系统的准确建模，而是系统合适的简化建模。

在仿真过程中，如图3的曲线：表示的是系统状态量随时间变化的结果，如图4的曲线：表示的是控制量随时间变化的结果，状态量偏差随时间变化的关系就如图5所示。

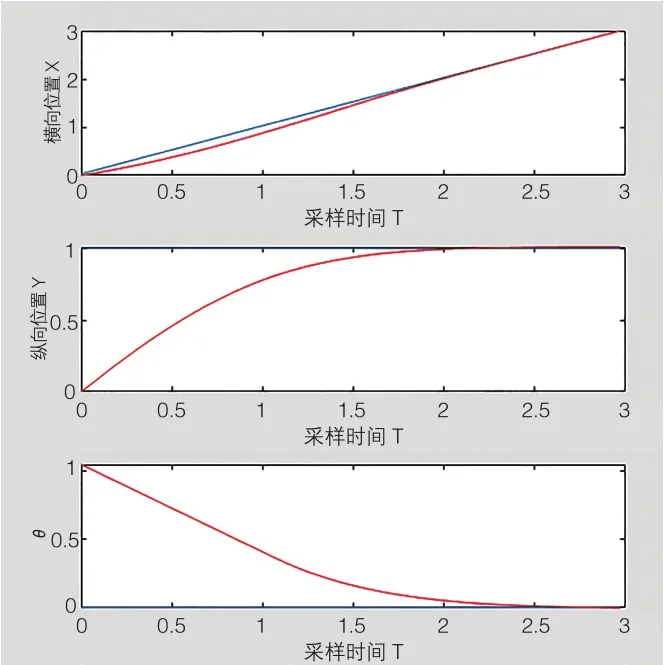
图3 系统状态量随时间变化曲线

图4 控制量随时间变化曲线

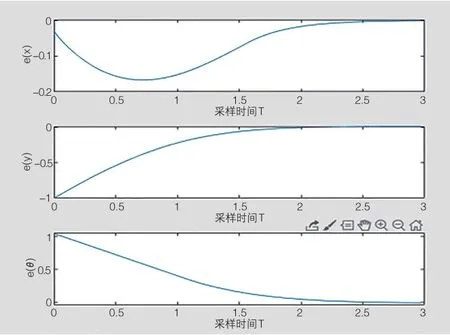
图5 状态量偏差随时间变化

所得结果误差在合理范围内，即证明了本文设计的自适应全局渐进跟踪控制器的真实性与可靠性。

5 总结

轨迹跟踪的重点有两个，一是轨迹跟踪的稳定性，二是控制系统的复杂性，这些都是国内外学者研究的热点问题。针对智能工厂内无人车轨迹跟踪精度低的问题，本文主要的研究内容如下：

建立无人搬运车动力学和运动学模型，采用Lyapunov直接法设计自适应全局渐进跟踪控制器，对该控制器进行仿真实验，仿真结果表明所研究的跟踪控制器是可行的，能够提高无人车的跟踪精度和稳定性。

上述实验证明了自适应全局渐进跟踪控制器的真实性与有效性，研究基本可以达到预期的目标，能够为智能工厂实现精准化和智能化的无人驾驶技术提供理论依据和实验基础。此外，仍存在以下问题：

1.由于仿真实验与真实的车辆之间具有一定差异，因此在环境地图探索构建中可能会出现车辆不能识别或避开障碍物等问题。

2.因为算法简单，环境地图过于复杂，导致全局规划和本地规划路径之间的差距太大，从而影响了车辆的任务和效率。