面向制造业的窄带物联网覆盖类别更新的仿真优化研究

吴菁晶

（东北大学 计算机科学与工程学院，辽宁 沈阳 110819）

0 引 言

随着物联网技术的飞速发展以及移动通信开始走向物与物的连接，传统的通信技术在成本、灵活性和覆盖性等方面已经无法满足日益增长的用户需求，面临着越来越多的挑战；而一种新的通信技术—窄带物联网（Narrow Band Internet of Things, NB-IoT）[1]的出现对现有的通信体系产生了革命性的影响。NB-IoT的关键技术主要由长期演进（Long Term Evolution, LTE）技术发展而来，当然也有对应其特点的技术革新。例如对窄带资源的利用再辅以路径损耗更低、绕射能力更强的低频部署，并支持多次的重传，从而实现广覆盖和深覆盖[2-3]。

覆 盖 类 别[4]是 3GPP（The 3rd Generation Partnership Project）针对NB-IoT引入的概念，即覆盖增强等级（Coverage Enhancement Level）。在先前的R13协议中，3GPP根据最大耦合损耗（MCL, Maximum Coupling Loss）定义了0、1、2共三个等级，可分别对抗144 dB、154 dB、164 dB的信号衰减。NB-IoT覆盖增强机制的基本思想是以更多的成功接入次数交换更多的传输功率，即在较差的信道环境中为NB-IoT终端分配更多的传输时间以积累更多的发射功率。在R15版本中，基于NB-IoT的覆盖类别定义已扩展到四个[5-6]。

当NB-IoT基站的覆盖半径[7]较大或NB-IoT终端部署在工作环境不理想的信道（如车库、地下室等）时，所有终端的覆盖类别相同会导致终端处于令人不满意的工作环境中，性能会急剧下降。预计不同的覆盖类别将增加系统访问成功的可能性，降低系统功耗并提高整体系统性能。目前，NB-IoT已逐渐成为学术界、行业内和标准化组织内的热门话题[8-9]。未来的低速率区域将越来越多地依赖这些技术和标准，NB-IoT的新技术将被更广泛地应用，并促进通信技术的不断发展。

本文针对NB-IoT的覆盖类别更新问题进行研究，建立了基于马尔可夫链的过程模型，并应用智能算法对问题进行求解。

1 NB-IoT覆盖类别更新算法建模

当信道环境发生变化导致连续接入失败/成功次数达到当前覆盖类别中规定的最大数量时，NB-IoT需要做出覆盖类别的更新调整[10]。以往这些更新都是静态的，导致很多相关的研究和应用都有局限性。因此，本文为了降低一般性能指标平均接入失败概率和减少功耗，提出了优化的动态类别更新模型，在系统正常运行时就采取一定的措施来提高系统性能。

如图1所示，初始判决覆盖类别为2时可能发生的状况为：经过最初的判决将覆盖类别定位到2上，若此时可在覆盖类别2上良好传输且一直成功传输到上限N2,max次，判决认定可以到更低级别的覆盖类别1，否则就在覆盖类别2上传输信息；覆盖类别1和0的情况同上。参考上行链路自适应和覆盖类别更新模型的部分内容研究出了有返回状态的优化过程。

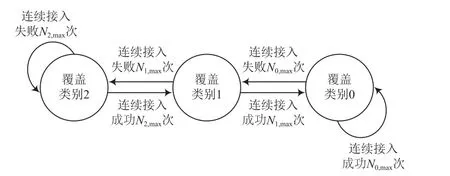
图1 覆盖类别更新优化过程模型

马尔可夫链模型是一个随机变量序列，它与系统的状态相对应，而此系统在某个时刻的状态只依赖于它在前一时刻的状态。其特性各行元素之和为：

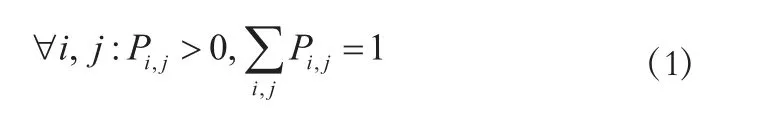
从覆盖类别更新过程可以看出，该过程可分为多个覆盖类别状态，各状态只与它之前的状态有关。因此，此随机过程可以运用马尔可夫链模型展示，只需要把相对应的条件转化为概率。状态转化只在相邻的两种状态中出现。k种覆盖类别的马尔可夫链模型需要参数设定，见表1所列。

表1 模型所需参数及其符号

若用Pi,j表示从覆盖类别i到覆盖类别j的概率，可以较容易地得到转移状态矩阵为：

也很容易发现该马尔可夫链为不可约且非周期，所以存在平稳分布，便可求出该矩阵的稳态概率分布为：

当k=3时，便是覆盖类别更新机制的马尔可夫链模型。在得出过程模型后便可以以失败接入概率和功耗等变量为目标求解模型的最优化参数。

2 NB-IoT覆盖类别更新算法优化

本章通过优化设计算法对前文建立的覆盖类别更新模型进行求解，得出模型的状态转移矩阵，然后求解出模型的稳态分布，最后通过公式分析约束条件设计遗传算法。

根据上文建立的模型，利用在每个覆盖类别的单次接入成功/失败概率的最大接入成功/失败次数的几次方，即可表示各覆盖类别状态之间的转移条件；再辅以马尔可夫链的特性，可以得到状态转移矩阵为：

式中：P[i, j]表示从覆盖类别i转移到覆盖类别j的概率，例如此处第一项为P[0, 0]，即是类别0转移到类别0的概率；Pd,i表示在覆盖类别i处的单次接入失败概率；Nd,i表示在覆盖类别i处最多接入失败次数；，表示接入失败N次后从类别0转移到了类别1，P[1，2]同理；在类别1处若设Ps,i+Pd,i=1，即单次失败概率加上成功概率为1，所以成功Ns,1次后就会从类别1回到类别0，即P[1，0]，类别3同理。其余项根据式（8）可得。以上便可完整地表示3个状态类别的覆盖类别更新算法。

平稳分布亦称不变测度（invariant measure）。假设在总功耗E下有一种概率分布会使马尔可夫过程成为平稳随机过程，给定以E={0, 1, ...}为状态空间的马尔可夫链，其转移概率矩阵为P。如果存在总功耗E下的概率分布Π=（Π0, Π1, ...）满足矩阵方程：

则称Π为链的平稳分布，或称为转移矩阵P的不变测度。故将式（8）代入式（9）可得：

以不同重复次数下减少失败概率和降低功耗为目标。为简化分析可令Ns,i=Nd,i=Ni,max，得到平稳分布后将每种覆盖类别的失败概率和功耗分别乘以相对应的Π，最后相加即可得到平均的失败概率和功耗如下：

式中，Pk-1表示在k-1覆盖类别下的总失败概率。

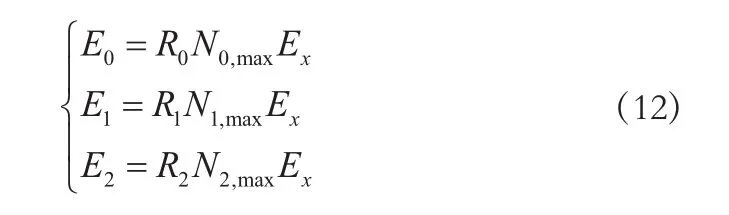
式中：Rk-1表示在覆盖类别k-1下可重复传输的次数；Ex表示建立一次连接需要的功耗；Ek-1表示在覆盖类别k-1下消耗的总功耗。

由此，展开式（4）得到：

式中，Pd,k-1表示在k-1覆盖类别下的单次接入失败概率。为了简化并与功耗相关参数结合，Pd,k-1可表示为由外界原因引起的失败概率Pd和由重复次数累计减少的失败概率的乘积（NB-IoT随机接入的特点：以重复次数换取更小的接入失败概率，但是增加了功耗）。Pd在同一环境中可视为定值。

同理，展开式（5）得到：

显然Pa和E都与一些整数类型参数有关，理论上可以用约束条件和遍历算法求解，是一个求解最优解的过程，而遗传算法正好符合这个特性。

遗传算法是一种比较基础通用的计算模型，模拟了达尔文生物进化理论的自然演化和遗传机制的生物进化过程。它是一种通过模拟自然进化过程来搜索最优解的方法。覆盖类别更新的遗传算法如图2所示。

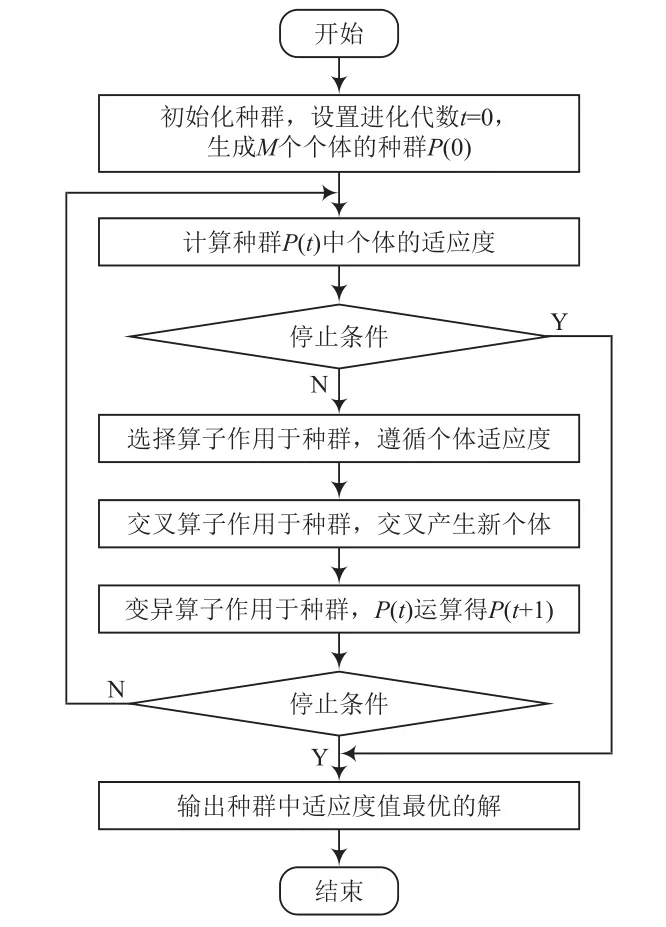
图2 覆盖类别更新的遗传算法流程

由上述分析，目标平均接入失败概率和平均功耗只与各覆盖类别最大传输次数Nk-1,max、重复传输次数Rk-1和全局最大次数N有关。

3 NB-IoT覆盖类别更新算法优化仿真

针对目标函数Pa和E，仿真分析它们与各参数之间的关系。图3（a）、图3（b）、图3（c）展示了确定参数Rk-1={1, 2, 4}、N=200、Ex=3.56×10-7Wh情况下Nk-1,max与Pa和E的关系。

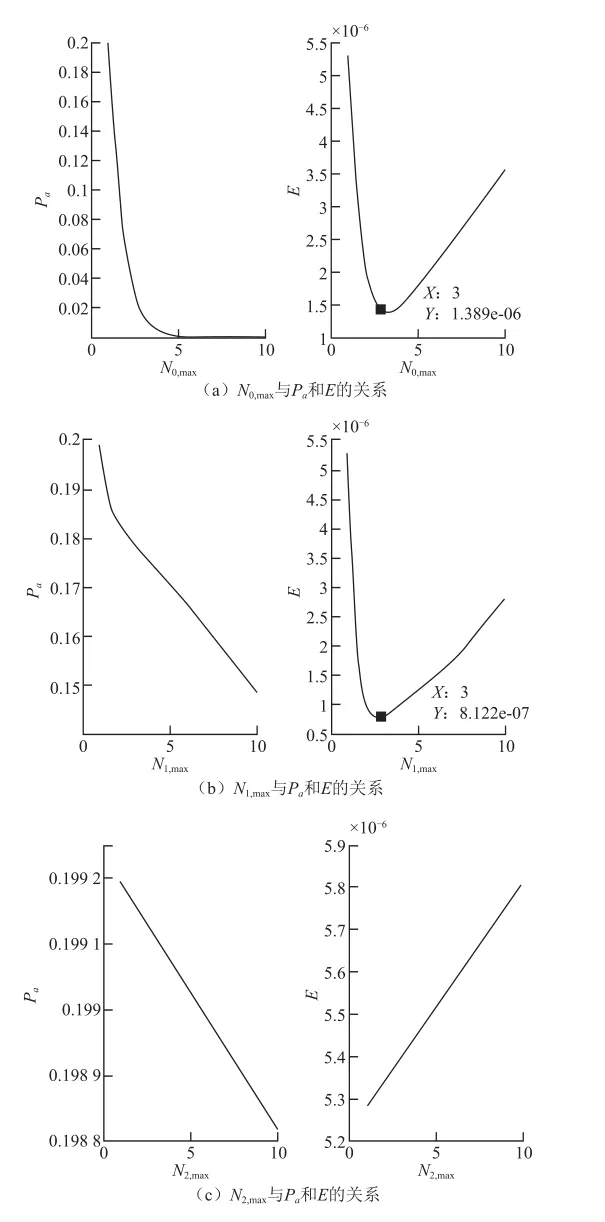
图3 各参数与Pa和E关系的仿真结果

仿真结果证明，Pa与N0,max的关系曲线呈现负指数下降趋势，随N1,max增加而下降，与N2,max的关系曲线大致呈线性下降趋势，这与NB-IoT随机过程的以接入次数换取成功概率的特征相符合。功耗E随N0,max和N1,max先下降再上升，随N2,max增加而增加。显然N0,max和N1,max在此条件下存在最小值，而N2,max尽可能取最小，该条件下的最优解为[3，3，1]。

4 结 语

当NB-IoT基站的信道环境发生变化导致连续接入失败/成功次数达到当前覆盖类别中规定的最大数量时，NB-IoT需要做出覆盖类别的更新调整。本文为了降低一般性能指标平均接入失败概率和减少功耗，针对NB-IoT的覆盖类别更新问题进行研究，建立了基于马尔可夫链的过程模型，并应用智能算法对问题进行求解。仿真结果表明，基于遗传算法能够在一定条件下找到最优解，结合参数分析验证了其正确性，并能有效降低接入失败概率，减少系统功耗。