车载动力电池箱壁板抗振疲劳分析

田天池张洪信韩明轩

(青岛大学机电工程学院,山东 青岛 260071)

为了实现汽车产能的改变,新能源汽车的发展愈发凸显优势。对于电动汽车的研究,重点之一是动力电池技术,好的动力电池能够提高电动汽车的续航能力和安全性能[1]。电动汽车电池箱的核心部件是动力电池包,安全性十分重要,对整车的安全性、稳定性有着直接的影响,电池组质量较大会对汽车的可靠性和驾驶安全性产生影响[2]。本文对动力电池箱进行全面的分析,以及可靠性验证。动力电池箱的可靠性分析,已经有一些研究方法。杨书建对某型电池箱进行优化设计,合理布置了顶盖和地板的加强筋分布[3]。冯富春等人[4]建立动力电池箱三维模型,其模态分析结果显示,电池箱的前6阶频率不在路面激励频率范围内,具有良好的抗震性能;XIA Y 等人[5]分析了地面对电池箱底部受到冲击的情况,对电池箱防护结构进行改进。秦毓等人[6]对动力电池箱进行轻量化设计,通过对电池箱稳、瞬态性能进行分析,对各零件形貌和尺寸做了优化;M.HARTMANN 等人[7]利用Optistruct对电池箱箱体进行形貌优化,实现轻量化设计;邓腾树等人[8]对某型纯电动汽车的动力电池箱模态分析分析,本文参考其优化结果建立动力电池箱模型;梁冲等人[9]对某型动力电池箱研究,电池箱的强度、刚度得到改善并实现了电池箱轻量化。目前对于电池箱的可靠性研究,主要有刚度、强度、模态、结构优化等,软件中实现在一定加载条件下的求解结果满足安全性要求,没有考虑振动引发的裂纹、疲劳受损问题,实际的情况是电池箱受到振动会由振动引发断裂等问题,使薄弱位置满足安全性要求才更符合现实意义,本文研究振动薄弱位置的断裂应力和疲劳分析,对于系统的研究此类问题具有指导意义。

1 动力电池箱模态分析

1.1 结构参数

模态分析是疲劳破坏分析的前提,需要根据结构参数建立电池箱的有限元分析模型。根据某品牌的动力电池箱实物,简化处理后建立动力电池箱几何模型,电池箱主要有电池、箱体、电池管理系统等部分组成,为了便于有限元计算,将模型简化为电池箱箱盖、箱体、底板3部分,电池箱结构简图如图1所示。

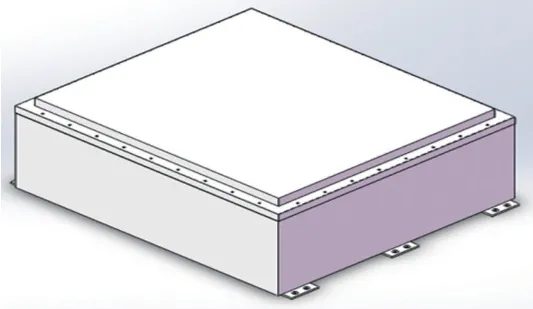
图1 电池箱结构简图

该电池箱的材料为普通碳素结构钢Q235,Q235材料参数如表1所示。

表1 Q235材料参数

1.2 模态分析

汽车行驶过程中,因路面不平度、电机转动等产生激振,从而传递给电池箱,但通常处理为电池箱随车架共振,大约为20～30 Hz。模态分析通过模拟动力电池箱受到的激励,找出动力电池箱在低阶振动频率下的共振频率,得出电池箱的固有频率,与外界的激励进行对比,避免在实际工作过程中共振对动力电池箱箱体造成破坏[10]。

根据达朗贝尔原理,惯性力引入当前研究的系统,建立电池箱有限元动力学微分方程[11]为

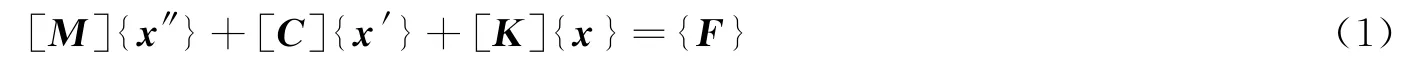
其中,[M]、[K] 和[C] 分别代表结构系统的质量矩阵、刚度矩阵和阻尼矩阵;{x″}、{x′}、{x} 分别代表单元节点上的加速度列阵、速度列阵、位移列阵;{F}是外力矩阵[12]。无阻尼自由振动方程为

通过坐标变换,式(2)的解为

其中,u是{x} 振幅列向量;ω是固有角频率。合并式(2)和式(3),得

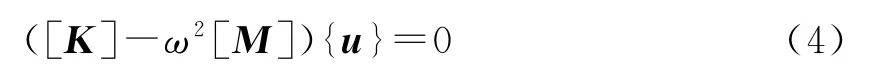
式中,ω为各个阶数所得的固有角频率的大小,振动频率为f＝ω/(2π)。将电池箱模型文件导入Hyper Mesh中,由于模型的厚度相比长、宽小很多。在网格划分过程中,采用抽取中面的方式进行网格划分,网格划分结果如图2所示。

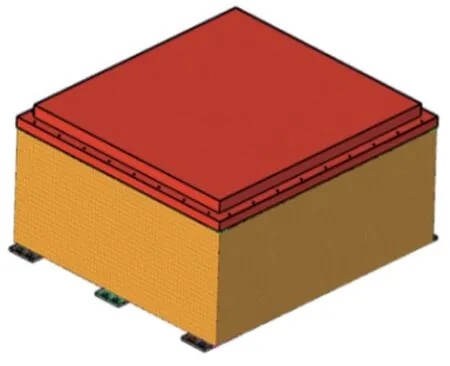
图2 网格划分结果

计算模态分析时,计算模态阶数越高,网格划分越细密[13],本研究后续进行前六阶模态分析,动力电池箱体的高度为所取网格尺寸的20倍。

模态分析结果如图3所示,由图3可以看出,动力电池箱低频范围是一阶和二阶,分别位于下箱体底部和箱盖顶部中心。

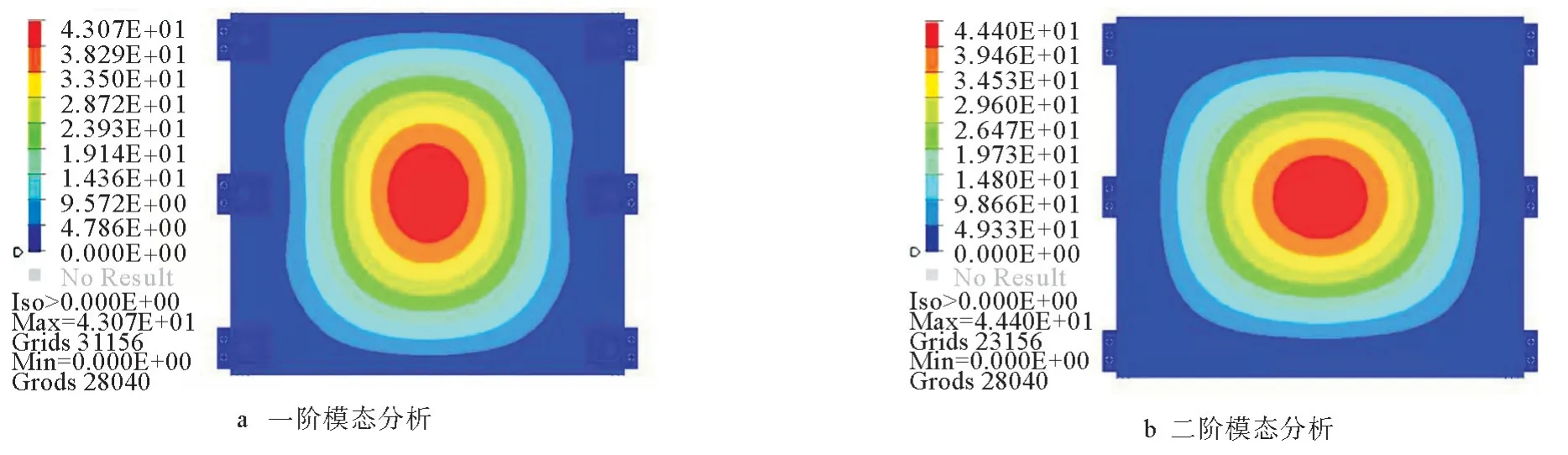
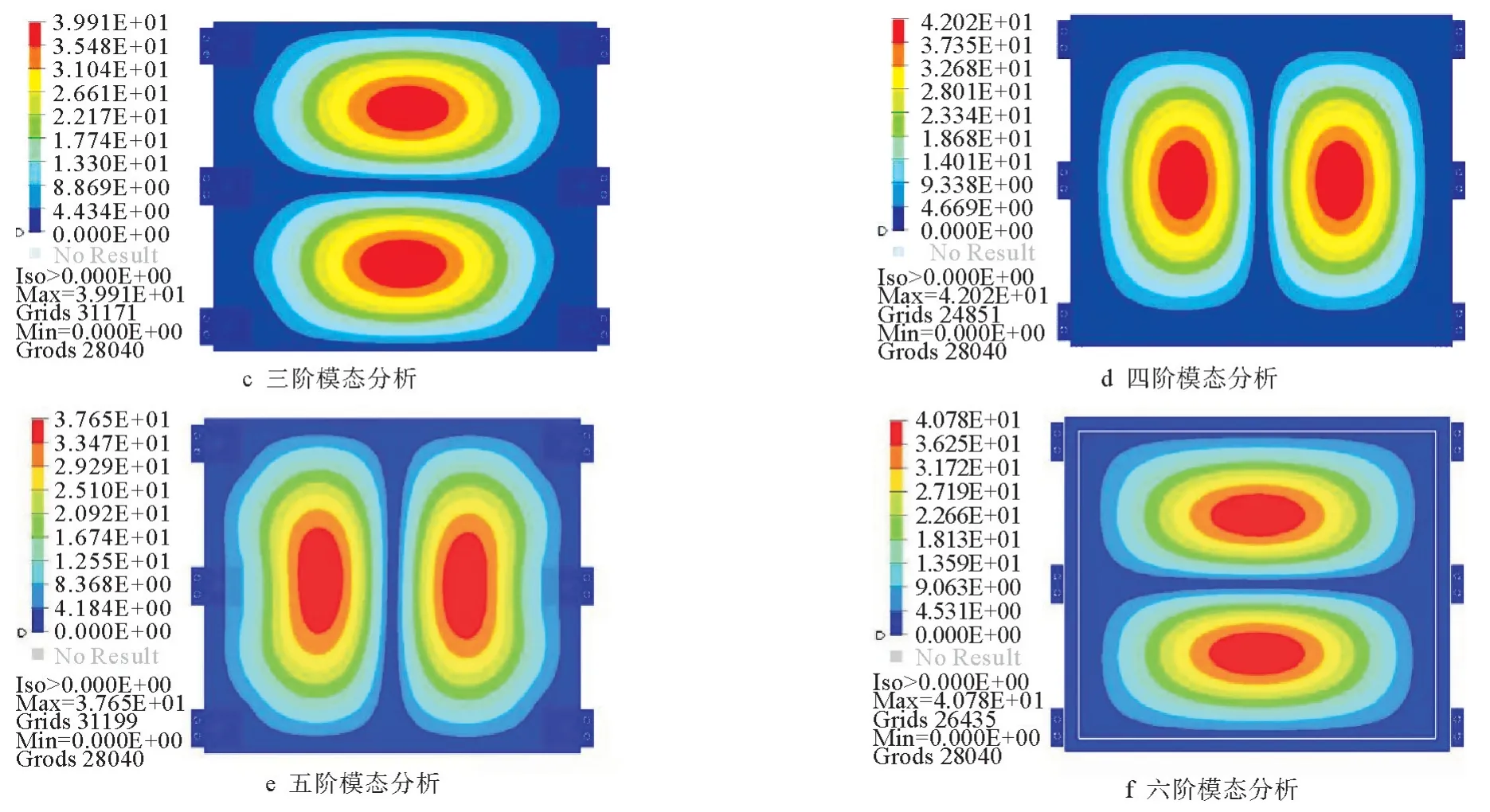
图3 模态分析结果

通过模态分析固有频率及位置,模态分析结果如表2所示。由表2可以看出,随着阶次提升,固有频率也在增大,动力电池箱的薄弱位置在不同区域。根据经验,在激励频率为30 Hz以下时,对动力电池箱的影响较大,在此频率下要尽量避免共振。一阶模态频率为22.79 Hz,二阶模态频率为23.54 Hz,处在箱盖顶部中心,电池箱的箱体和箱盖刚度不足,需要升高一、二阶固有频率。

表2 模态分析结果

2 电池箱随机振动分析

2.1 随机振动理论

随机振动仿真即研究动力电池箱时刻在随机激励下的响应,是一种概率统计方法。本章对动力电池箱进行随机振动仿真,使用Hyper Mesh的Optistruct模块将功率谱密度作为随机振动的激励谱。假设符合正态(高斯)分布的同时,随机变量的集合平均值为零,随机过程中定义随机变量X(t),自功率谱密度函数Sxx ω() 式(5)和自相关函数φxx τ() 式(6)可由傅里叶变换互相转换

其中,ω是固有频率;j是虚数单位;τ是期望。

随机变量X(t)和Y(t)为互相关函数,互相关函数为式(7),互谱密度函数为

令τ＝0,得X(t)方差方程为

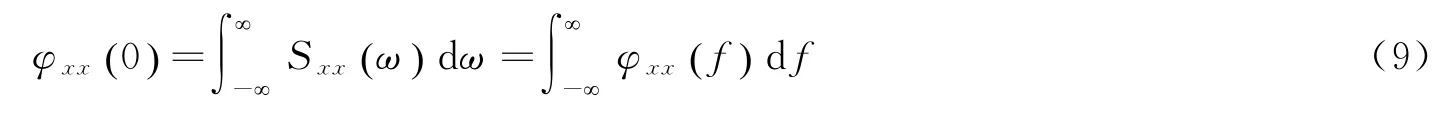
X(t)的均方根值为

仿真计算得xrms应力值,即1σ等效应力。根据正态(高斯)分布提出的三区间法,分为±1σ、±2σ和±3σ区间等效应力水平,计算得到的应力值分布在各等效应力水平区间的概率。高斯三区间法如表3所示。

表3 高斯三区间法

高斯三区间法是将应力按照正态分布化分为3个区间,分别计算3个区间的应力,将3个区间的响应分析结果线性叠[14～15]加。本文使用高斯三区间法,判定应力强度是否满足结构要求。

2.2 随机振动分析

通过Hyper Mesh软件,对随机振动分析进行设定。前处理约束示意图如图4所示。

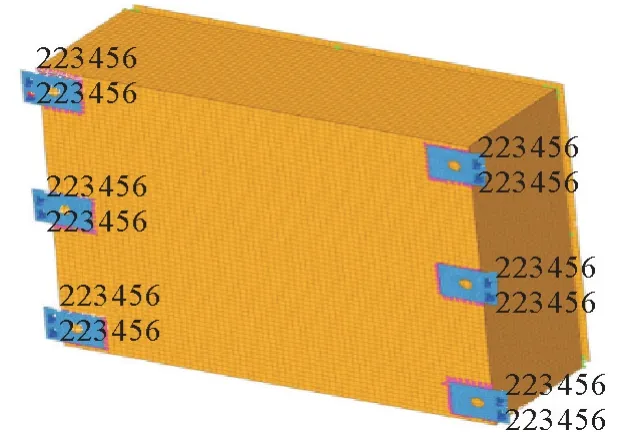
图4 前处理约束示意图

螺栓孔X、Y、Z3个方向约束自由度,施加1 g的单位载荷,频率范围定为5～200 Hz,定义求解初始频率5 Hz、增量频率2.5 Hz,频率增量数78 Hz,求解范围0～500 Hz,在托架的螺栓孔施加固定约束。完成求解设置,得到X、Y、Z3个方向应力云图如图5所示。

图5 X、Y、Z 3个方向应力云图

由图5可以看出,电池箱X方向振动工况的最大应力,其中,1σ应力为37.09 MPa,3σ应力为111.27 MPa,应力值较小,结构强度满足要求。电池箱Y方向振动工况最大应力,其中,1σ应力64.61 MPa,3σ应力是193.83 MPa,应力值较小,结构强度满足要求。电池箱Z方向振动工况最大应力,其中,1σ应力77.9 MPa,3σ应力是233.7 MPa,应力值较小,结构强度满足要求。

3 电池箱疲劳破坏分析

3.1 裂纹断裂判据

在线弹性条件下,低应力脆性裂纹处断裂的判据为式为

其中,K为应力强度因子;KIC为材料的平面应变断裂韧性,通过对材料进行试验测量得到。当应力强度因子K＞KIC时,裂纹发生扩展。本文涉及的动力电池箱的材料为Q235,经试验测其平面应变断裂韧性为KIC＝191.4 MPa·mm1/2

3.2 动力电池箱表面裂纹应力强度系数

平面半椭圆型裂纹应力强度因子K1,裂纹尖端应力场的强弱程度可以由裂纹的应力强度因子表述[16]

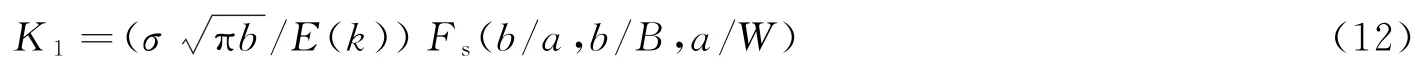
其中,a、b分别为椭圆的半长轴、半短轴;B为板厚;W为板宽。椭圆积分表达式为

裂纹的几何修正函数方程式为

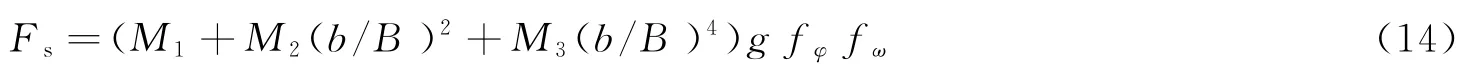
其中,M1、M2和M3是长半轴与短半轴的关系表达式,M1＝1.13－0.09(b/a),M2＝－0.54 ＋0.89/(0.2＋b/a),M3＝0.5－[1/(0.65＋b/a)]＋14(1－b/a)2;g为修正载荷;fφ为内嵌椭圆裂纹解的角度函数;fω为有限宽度校正函数。内嵌椭圆裂纹解的角度函数为

式中,φ为角函数角度;fω为有限宽度校正函数,即

经证明,当0≤b≤1/a且b/B≤0.8时,计算方法误差小于5%[17]。

在Workbench中完成材料定义、模型处理、施加边界条件、划分网格步骤和插入断裂工具,裂纹应力强度系数与裂纹扩展距离的关系如图6所示。由图6可知,裂纹处的I型裂纹应力强度系数的最大值为62.77 MPa·mm1/2,小于Q235材料的平面应变断裂韧性KIC,因此裂纹不会扩展,较为安全。

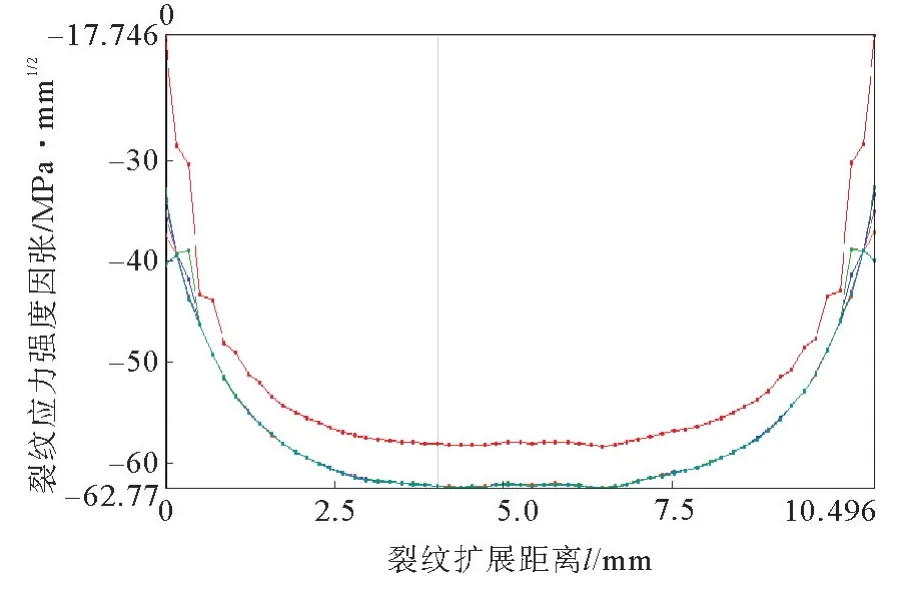
图6 裂纹应力强度系数与裂纹扩展距离的关系

4 动力电池箱疲劳寿命分析

4.1 疲劳寿命分析理论

1) 疲劳累计损伤理论。因为结构疲劳失效形成的机理较为复杂,所以机械领域中经常采用Miner线性疲劳累积损伤法计算结构疲劳寿命的均值[18]。结构吸收静功原理方程式为

式中,W1是动力电池箱循环数为n1时吸收的能量;W是动力电池箱疲劳破坏前吸收的总能量;N是动力电池箱总的循环次数。

动力电池箱吸收的能量会随着循环次数发生变化,假设加载过程由m个应力σ1,σ2,…,σm构成,各加载力对应的疲劳寿命分别为N1,N2,…,Nm,对应循环次数分别为n1,n2,…,nm,动力电池箱吸收的能量分别为W1,W2,…,Wm,得到结构吸收静功原理的一般方程式为

式中,D是部分疲劳损伤的线性叠加,当疲劳损伤的总和D达到1时[19],可以预测出现疲劳损伤失效。

2) 材料的疲劳特性。材料的疲劳性能用S-N曲线描述。当应力值S越小,材料的寿命值N就越大,当疲劳寿命循环N＞106次时,属于高周疲劳。材料S-N曲线的基本形式如图7所示。

由图7可以看出,该曲线分为Ⅰ、Ⅱ和Ⅲ分别表示低周、高周和亚疲劳区域[20],横轴是循环次数,纵轴是应力,应力越大,不发生破坏的循环次数越少。当在Ⅰ区时,会发生疲劳破坏,Ⅲ区表示无穷寿命。

图7 材料S-N 曲线的基本形式

通常情况下,标准的S-N曲线忽略了平均应力,而平均应力的存在会影响材料的疲劳极限的计算,所以要进行平均应力修正。使用Goodman法进行平均应力的修正为

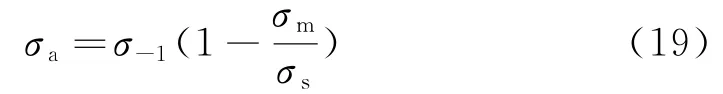
其中,σa是疲劳振幅极限应力;σ－1是对称循环下的疲劳极限应力;σm是平均应力;σs是屈服强度。

4.2 基于nCode Designlife的随机振动疲劳寿命仿真

通过Hyper Mesh软件,得到频率响应分析结果的传递函数,在nCode DesignLife软件中,选取Z方向上的加速度功率谱密度作为动态激励,联合疲劳累积损伤理论和材料的疲劳特性,预测动力电池箱的疲劳寿命。动力电池箱的235 材料,在nCode Design Life软件中,可以由强度极限、屈服极限、弹性模量等材料属性来得到相应的S-N曲线。对动力电池箱进行Z方向的随机振动疲劳寿命分析,Z方向随机振动疲劳寿命云图如图8所示。由图8可知,Z方向的最小疲劳寿命为2.369×105次,主要发生在箱盖中央和箱体底部中央。根据GB/T31467.3—2015中安全性测试振动试验的要求,每个方向进行随机振动测试的时间是21 h,即7.56×104s,比较可得Z方向的疲劳寿命符合国际要求。

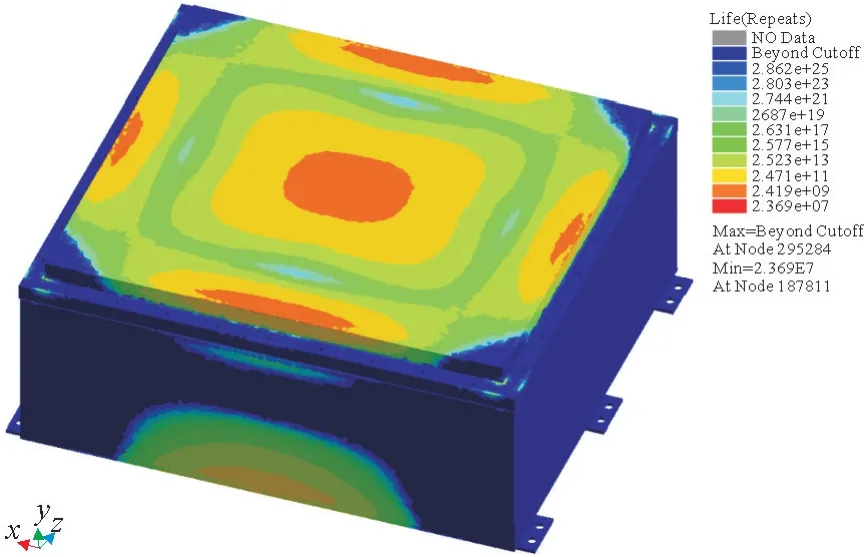
图8 Z 方向随机振动疲劳寿命云图

5 结束语

本文采用有限元方法,验证动力电池箱结构的疲劳可靠性。基于结构受载特点的网格划分原则,提高求解精度的把控,分别从模态分析、随机振动分析和疲劳分析入手,通过模态分析,激励频率小于固有频率,验证振动特性是安全的,通过随机振动验证强度可靠性,3σ小于屈服强度,通过疲劳分析,验证耐久可靠性。在理论指导的基础上,对电池箱的薄弱位置进行强度分析,验证薄弱位置强度符合第三强度理论,优化结构仿真的分析流程,得到满足工程要求的可靠性结果,对传统电池箱的结构设计具有知道借鉴意义。