考虑座椅设计对三维坐姿人体模型振动响应研究
陈 满赵清海杨景周贾继良
(青岛大学机电工程学院,山东 青岛 266071)
乘坐舒适性主要受路面不平度、轮胎、悬架系统、座椅设计、全身振动等参数影响,并取决于人体振动的持续时间、振幅和频率[1]。大量研究表明,人体对垂直方向4~10 Hz和水平方向0.5~3 Hz的振动频率最敏感[2]。因此,如何分析、预测和改善人体振动引起学者们的广泛关注[3]。近年来,国内外许多学者对多种动力学模型进行研究[4]。R.COERMANN[5]提出了一种单自由度模型,该模型将整个人体比作只有垂向运动的质量块;WEI L 等人[6--7]对单自由度模型进行了改进,建立了以头部和身体为代表的线性两自由度模型;P.BOILEAU 等人[8]提出了一种四自由度线性模型;张志飞等人[9]将集中参数模型与动力学模型相结合,建立了六自由度模型,并对模型进行了参数辨识;刘菲菲等人[10]建立了无座椅靠背的七自由度模型,并在不同频率下对人体进行振动试验;K.S.KIM 等人[11]建立了五自由度模型,很好地拟合人体在垂向和水平方向的表观质量;朱跃等人[12]通过对三自由度座椅悬架进行滑膜控制,获得更佳的动态性能;张鄂等人[13]对人体振动特性进行研究,建立了多自由度坐姿垂向振动模型。对于人体结构,以上模型过于简化,为更好地表达人体各部位在振动中的响应特性,需建立更多部位和运动方向的动力学模型。CHO Y 等人[14]建立了带有座椅靠背的九自由度多体生物动力学模型;E.PENNESTRI等人[15]提出由6个人体元素和2个汽车环境元素组成的有限元模型;颜磷娟等人[16]建立了二维有限元模型,研究了头部在受到冲击情况下的生物力学响应;舒红宇等人[17]在低频多向振动试验中建立了十二自由度人体动力学模型;LIANG C C等人[18]提出十四自由度动力学模型,研究不同坐姿对人体振动的影响;WU J等人[19]建立了三维人体模型,人体可以实现垂向、横向和滚动振动。上述模型广泛应用于研究人体对全身振动的响应,但在研究中,座椅均设定为刚性座椅,忽略了座椅设计对人体振动特性的影响。P.B.KUMBHAR 等人[20]提出六自由度座椅模型,对二维人体动力学模型进行仿真,发现不同座椅设计对人体振动具有显著影响。基于此,本文通过六自由度座椅模型[20],研究不同座椅模型对人体振动响应,建立三维坐姿人体动力学模型,并通过试验获得人体各部分的振动传递率。同时,将试验数据与模型仿真数据进行拟合,通过遗传算法进行参数辨识,得到人体各部分结构参数,并通过人体结构参数对3种座椅模型进行对比分析。该设计对研究人体关键部位振动响应具有重要意义。
1 人体动力学模型和座椅模型
1.1 人体动力学模型建立
考虑在实际驾驶中振动的多向性,为更真实反应人体每部分的振动特性,提出了四十八自由度的三维坐姿人体动力学模型,人体多体动力学模型如图1 所示。该模型由脚、小腿、大腿、躯干和头部组成,每部分都有侧向、纵向、垂向、侧倾、俯仰和横摆六个自由度。每部分关节处用J表示,关节视为由弹簧和阻尼组成的衬套元件,可以实现转动和平动。C表示人体与座椅之间等效接触点,可以实现平动。考虑模型较为复杂,需建立全局坐标和局部坐标,O为全局坐标,G为局部坐标。其中,Gil(xgil,ygil,ygil)、Jil(xJil,yJil,yJil)和Cil(xcil,ycil,ycil)(i=1,2,3)分别表示左侧大腿、小腿和脚对应部位的质心、关节点和等效受力点的坐标;Gir(xgir,ygir,ygir)、Jir(xJir,yJir,yJir)和Cir(xcir,ycir,ycir))(i=1,2,3)分别表示右侧大腿、小腿和脚对应部位的质心、关节点和等效受力点的坐标;Gi(xgi,ygi,zgi)(i=4,5)表示躯干和头部的质心坐标;J4(xJ4,yJ4,zJ4)和C4(xc4,yc4,zc4)分别表示头部与躯干关节点坐标和躯干与座椅靠背的接触点坐标。其中,α为座椅靠背倾角,β为座椅坐垫倾角。
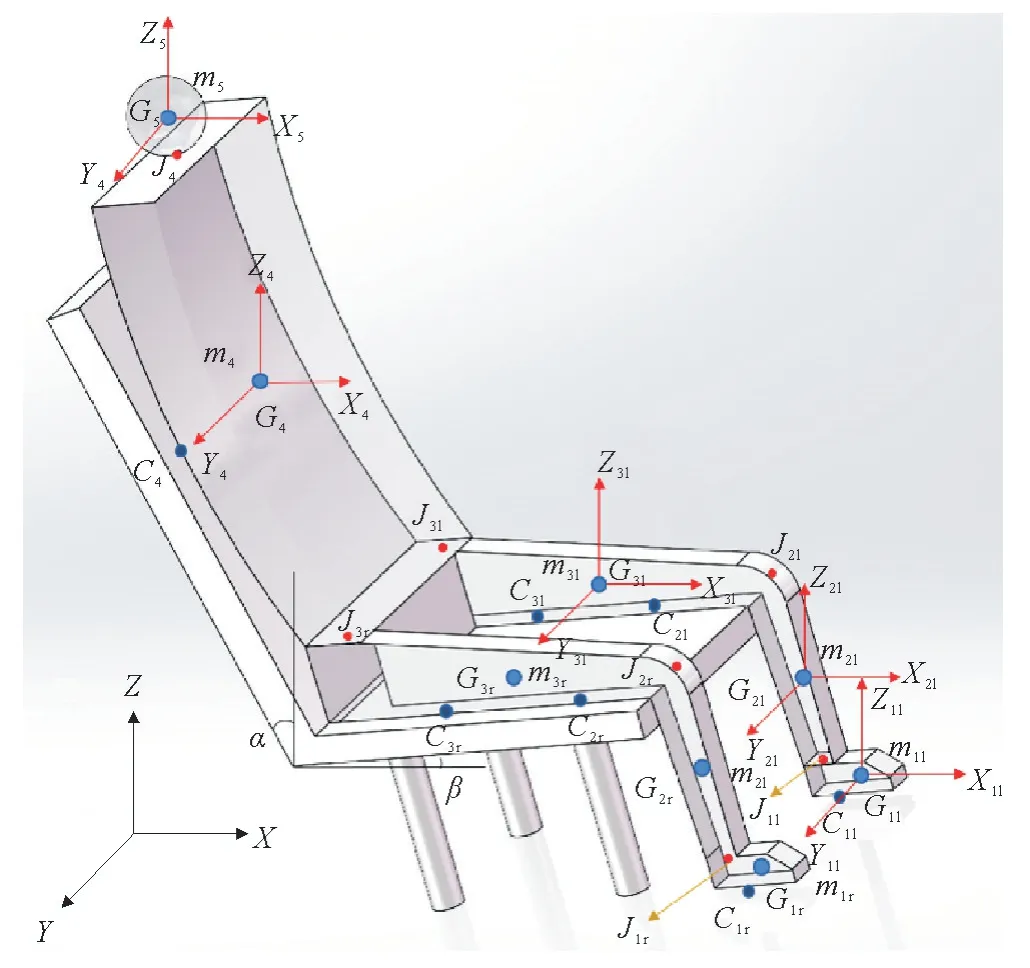
图1 人体多体动力学模型
结合人体各体段质量和转动惯量回归方程,计算其中1名试验者的人体参数。由于人体左右两侧的脚、小腿和大腿具有对称性,因此默认左右侧参数相同。以右侧为例,mi(i=1,2,…,5)表示对应于各部位的质量,每个部位用Bi(i=1,2,…,5)表示;(Iix,Iiy,Iiz)(i=1,2,…,5)表示人体部位mi绕其局部坐标各方向的转动惯量;(kix,kiy,kiz)和(cix,ciy,ciz)分别表示在Cir(l)(i=1,2,3)或Ci(i=4)点处弹簧和阻尼的水平移动刚度和阻尼系数;(kxi,kyi,kzi)和(cxi,cyi,czi)分别表示在Jir(l)(i=1,2,3)或Ji(i=4)点处弹簧和阻尼的水平移动刚度和阻尼系数;(krxi,kryi,krzi)和(crxi,cryi,crzi)分别表示在各关节点Jir(l)(i=1,2,3)或Ji(i=4)点处弹簧和阻尼绕X、Y、Z轴的转动刚度和阻尼系数;xi、yi、zi表示人体部位mi在振动过程中沿纵向、侧向和垂向产生的位移矢量;θix、θiy、θiz表示人体部位mi重心在振动过程中沿X、Y、Z旋转产生的角位移矢量;x0、y0、z0分别为振动台在纵向、侧向和垂向输入激励的位移矢量;θ0x、θ0y、θ0z表示振动台输入人体激励的转动角位移矢量。人体各部位质量和惯性特性如表1所示。

表1 人体各部位质量和惯性特性
1.2 3种座椅模型
3种座椅模型如图2所示。座椅模型分为3种情况,座椅模型1为无坐垫的硬座;座椅模型2为带坐垫但无座椅悬架的座椅;座椅模型3为带坐垫和座椅悬架的座椅。图2a中,忽略坐垫和靠垫对人体的作用,人体模型直接坐在一个硬座上,振动直接从座椅传递到人体;图2b中,人体模型与座椅模型之间增加了一个坐垫和靠背垫;图2c中,座椅模型在坐垫和靠背垫的基础上,在座椅和地面之间增加了座椅悬架,对座椅起到隔振作用。
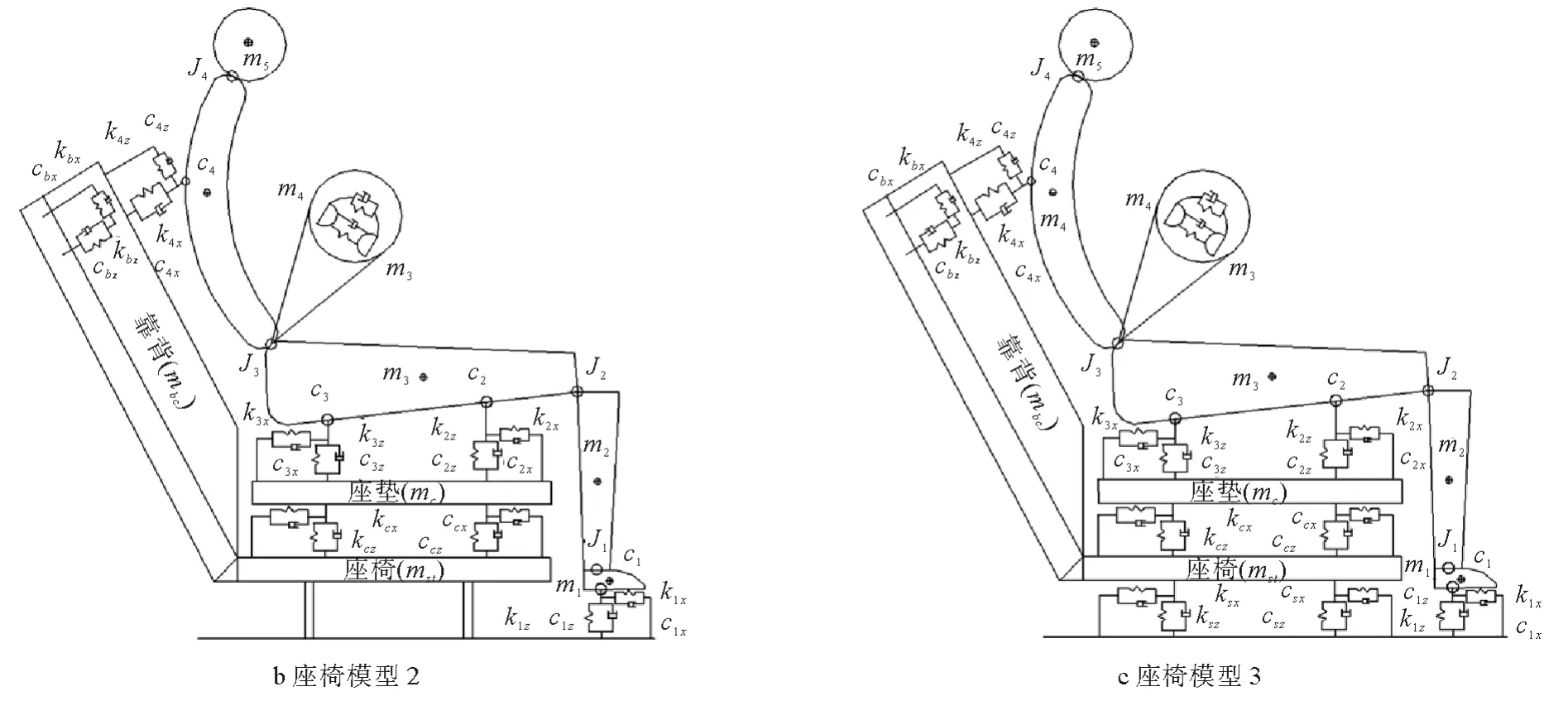
图2 3种座椅模型
为了简单方便,本研究认为坐垫和悬架的刚度和阻尼是线性的,用mc、mbc和mst分别表示坐垫质量、靠背垫质量和座椅质量,kcx、kcy、kcz和ccx、ccy、ccz分别表示坐垫3个方向的刚度和阻尼,kbx、kby、kbz和cbx、cby、cbz分别表示靠背垫3 个方向的 刚度和 阻尼。ksx、ksy、ksz和csx、csy、csz分别表示座椅悬架3个方向的刚度和阻尼。

座椅部件材料属性如表2所示。

表2 座椅部件材料属性
2 人椅模型动力学分析
由于座椅模型3较复杂,所以本文将以模型3为代表,通过不同的靠背角度和座椅角度对振动的响应,推导出人体各部分的动力学方程。以右脚m1为例,其动力学方程为
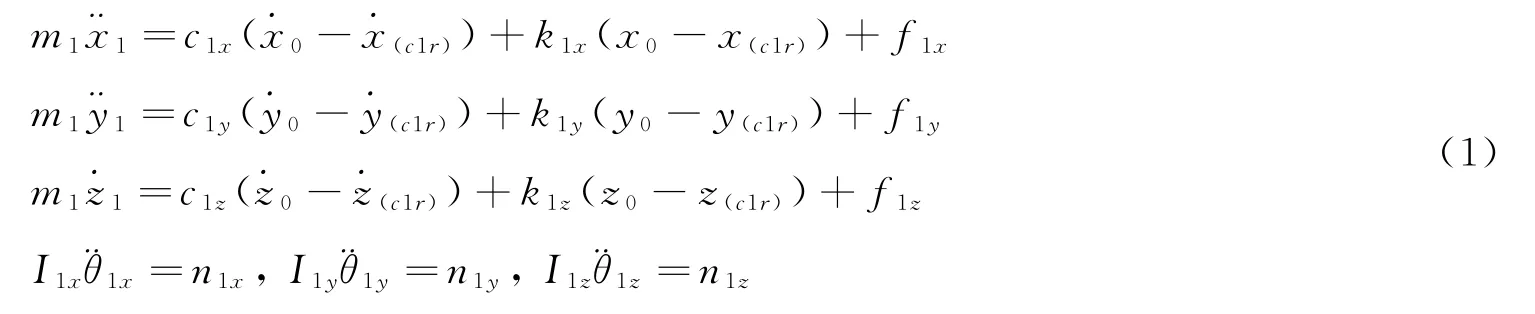
其中
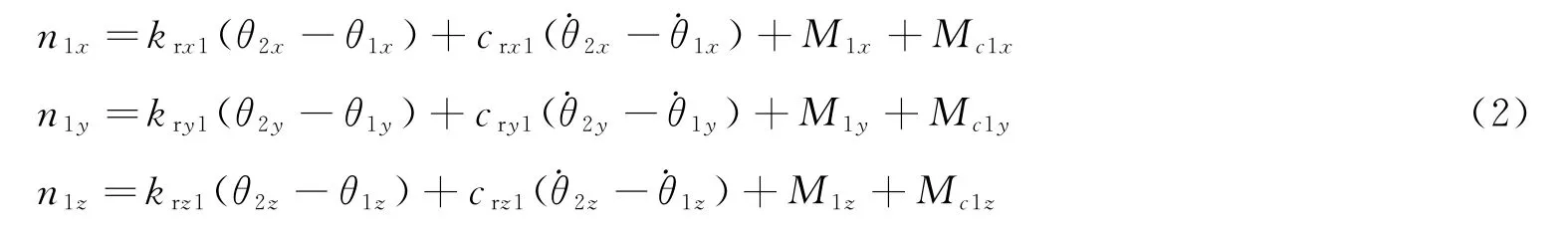
式中,x0、y0和z0分别为纵向、侧向和垂向振动输入位移;f1x、f1y和f1z分别表示关节J1在纵向、侧向和垂向所受到的作用力;θix、θiy和θiz分别表示人体部位mi在振动过程中旋转的角度;Mix、Miy和Miz分别表示关节J1对脚的质心产生的力矩;Mcix、Mciy和Mciz分别表示脚与地板接触点C1对脚的质心产生的力矩;n1x、n1y和n1z表示脚在振动过程中对其质心产生的力矩矢量和。脚的空间坐标变换矩阵为
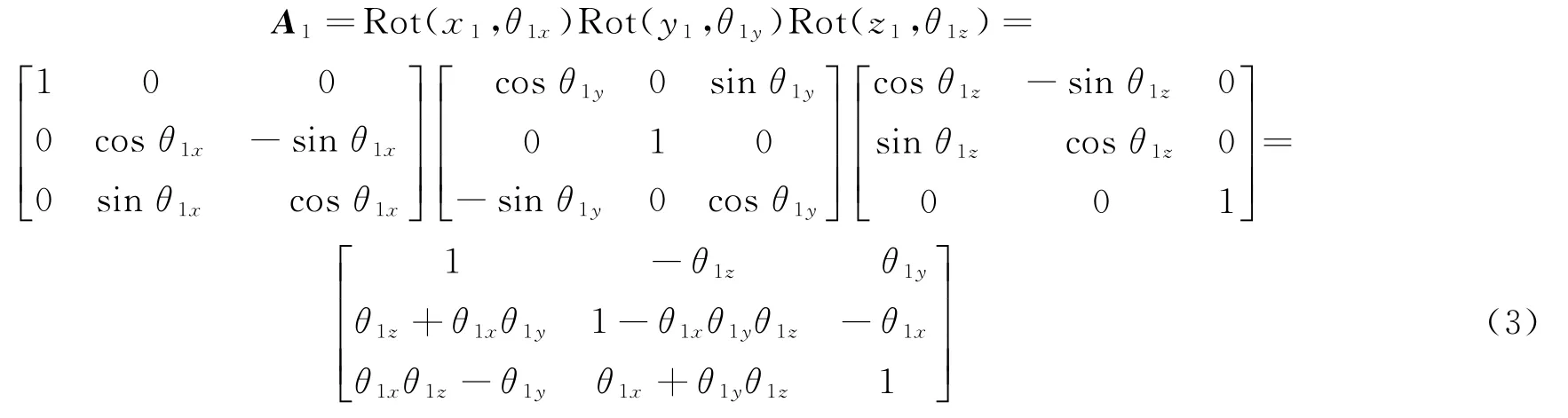
由于人体各部位转动的角度较小,因此忽略等二次项和等三次项,对矩阵A1进行线性化,得
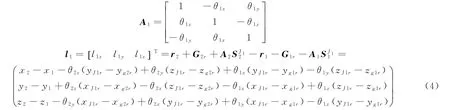
式中,l1表示小腿与脚关节点J1r在X、Y、Z上的位形向量。因此,在关节点J1r处所受到的作用力为
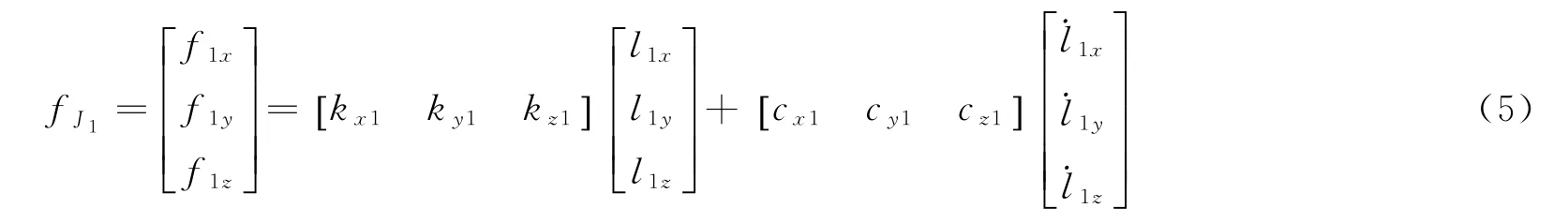
在振动过程中,关节点J1r相对于局部坐标G1r的空间坐标为
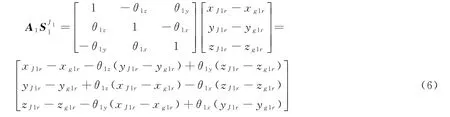
通过式(5)和式(6),求得关节点J1r对G1r点产生的力矩为
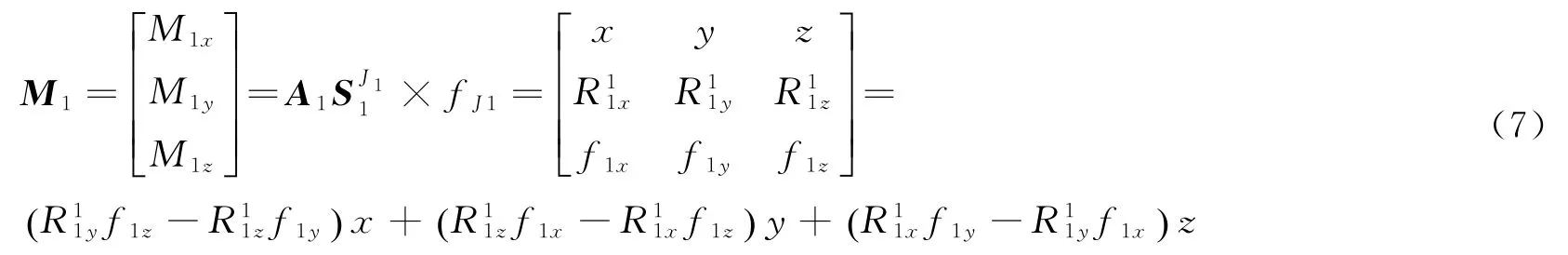
脚与地板接触点C1r对G1r点产生的力矩为
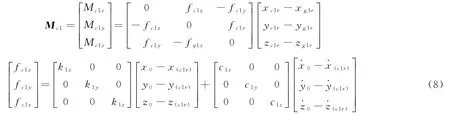
等效受力点C1r在振动过程中的位移为
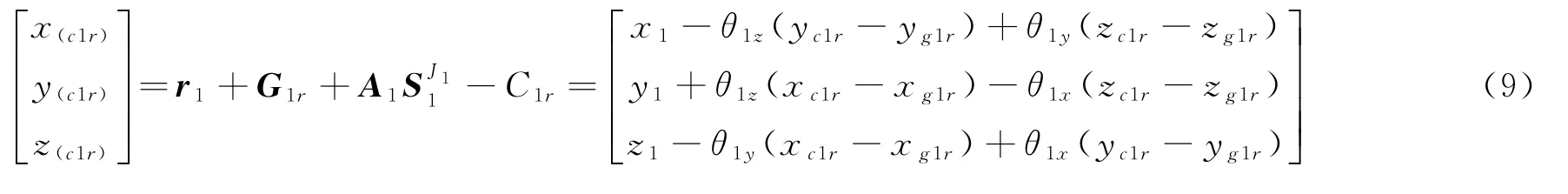
3 振动试验与参数辨识
3.1 振动试验
试验采用可根据需要调节坐垫和靠背倾角的刚性座椅,人体振动试验流程如图3所示。
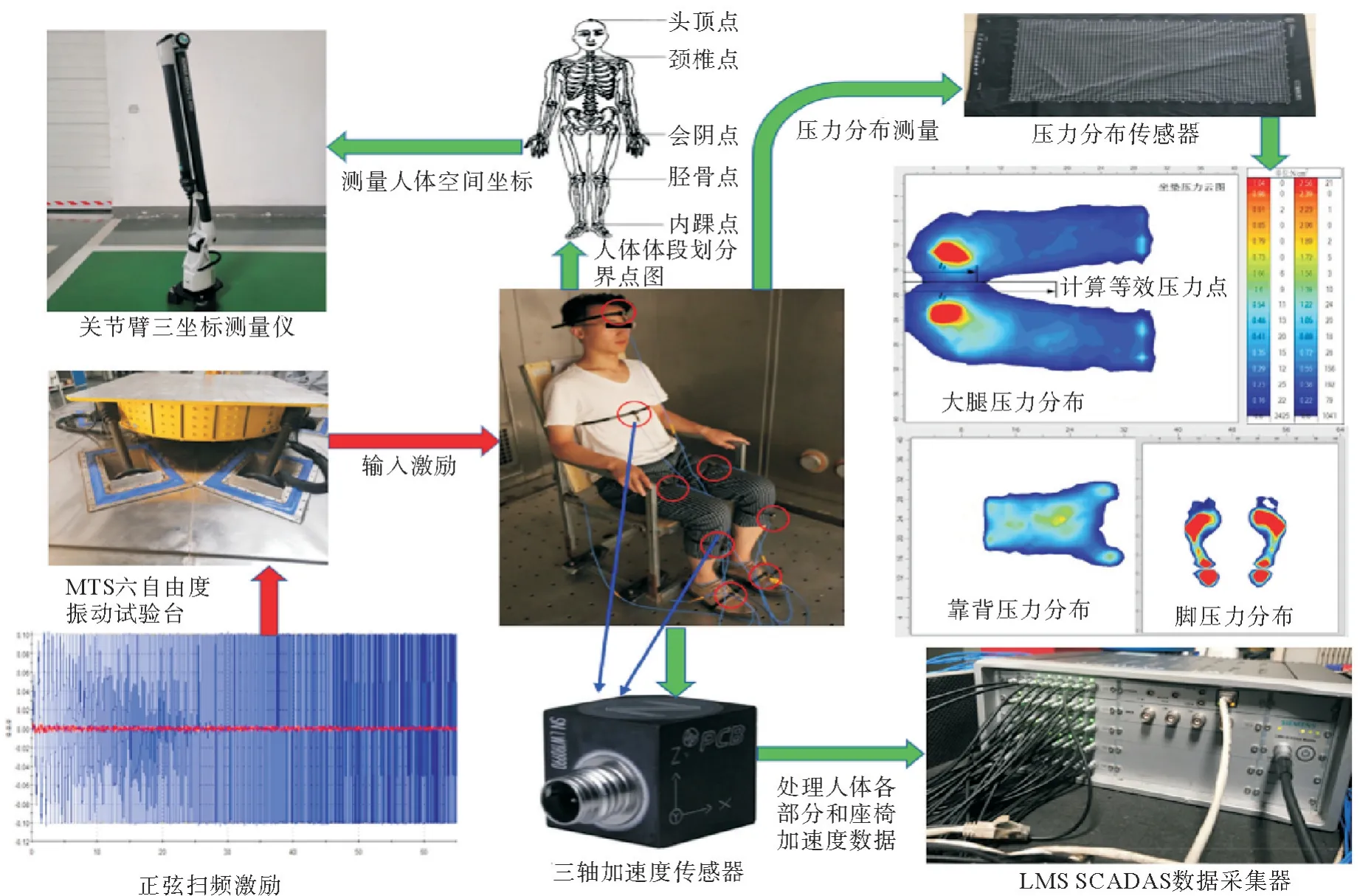
图3 人体振动试验流程
选择8名志愿者参与试验,年龄介于23~30岁,身高在170~173 cm,体重在65~68 kg,且身体健康,无肌肉、骨骼等身体疾病。通过三坐标测量仪,测出其中一位人体各部位的质心和关节点的空间坐标,关节点和质心点空间坐标如表3所示,等效接触点空间坐标如表4所示。

表3 关节点和质心点空间坐标

表4 等效接触点空间坐标
对试验台给予1~20 Hz的正弦扫频激励,每个方向上的激振强度均设定为1 m/s2。通过三轴加速度传感器测量人体的纵向、侧向和垂向的加速度数据,并通过LMS SCADAS数据采集器进行收集处理,得到8名志愿者在各方向的头部振动传递率与均值,8名试验者头部传递率与平均值如图4所示。
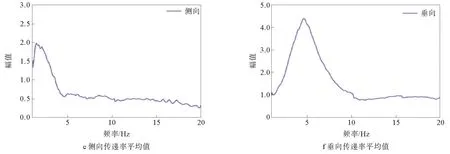
图4 8名试验者头部传递率与平均值
大腿、靠背和脚与座椅和地板之间的等效接触点,通过压力分布传感器测出的压力分布数据计算,其计算公式为
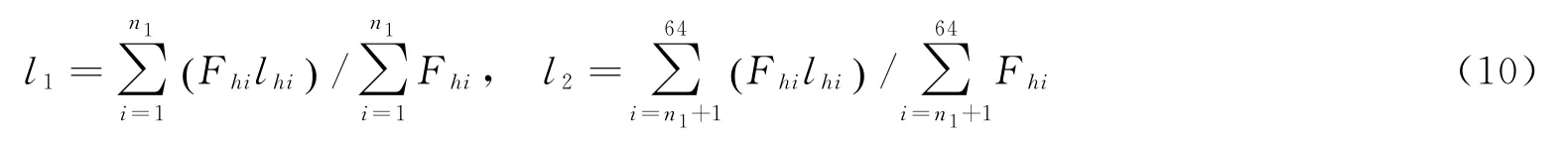
式中,Fhi是压力分布传感器上第i个方格区域压力;n1是对应其压力所在的方格号。
3.2 参数辨识
根据试验均值和数学模型进行拟合,通过遗传算法对人体纵向、侧向和垂向振动进行参数辨识。以垂向参数辨识为例,当人体受到垂向振动时,以垂向运动为主运动,侧倾运动为次运动,忽略其他方向的运动。设置待辨识参数为ζ,并对ζ的上界和下界设置边界条件,以垂向试验值与模型仿真值之差的平方和最小,建立目标函数,待辨识参数为
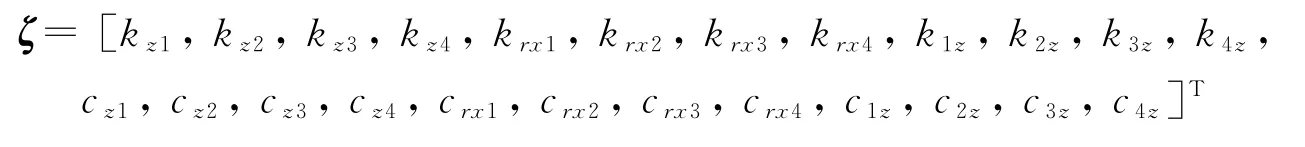
目标函数为
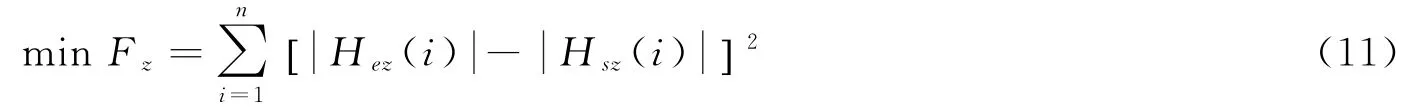
式中,Hez(i)表示在垂向振动方向上不同频率下的振动传递率试验值;Hsz(i)表示模型仿真计算值。
通过编写目标函数和遗传算法程序,最终得到人体各关节Ji和人体与座椅各接触点Ci的生物力学特性,人体模型的生物力学特性如表5所示。
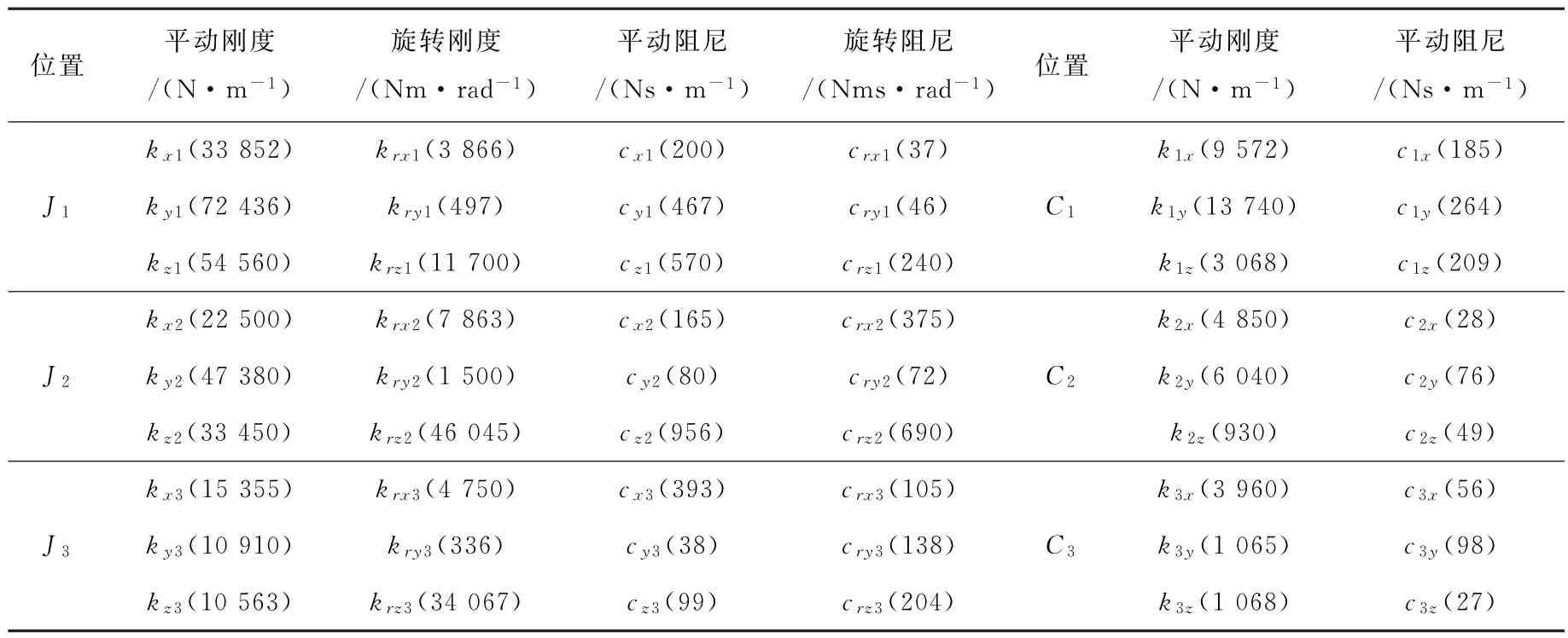
表5 人体模型的生物力学特性

续表5
4 3种模型对人体振动响应分析
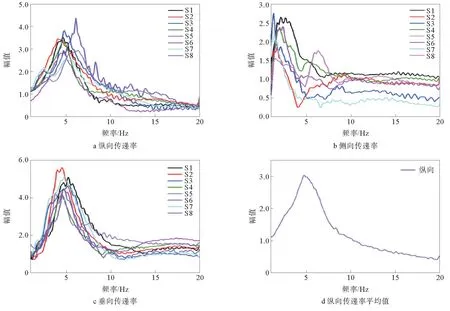
结合动力学方程,采用Matlab仿真,得到3种座椅模型中人体各部位在纵向、侧向和垂向的振动传递率。人体各部位纵向传递率如图5所示,图5a~5e分别为人体部位1~5在3种座椅模型中的纵向振动传递率。由图5可知,3种座椅模型对人体各部位的传递率曲线都具有一致性,在3~10 Hz内都具有高量值的传递率,与座椅模型1相比,座椅模型2对人体各部位的传递率明显下降,主要由于坐垫的增加降低了共振频率,说明坐垫可以衰减座椅对人体的纵向振动。
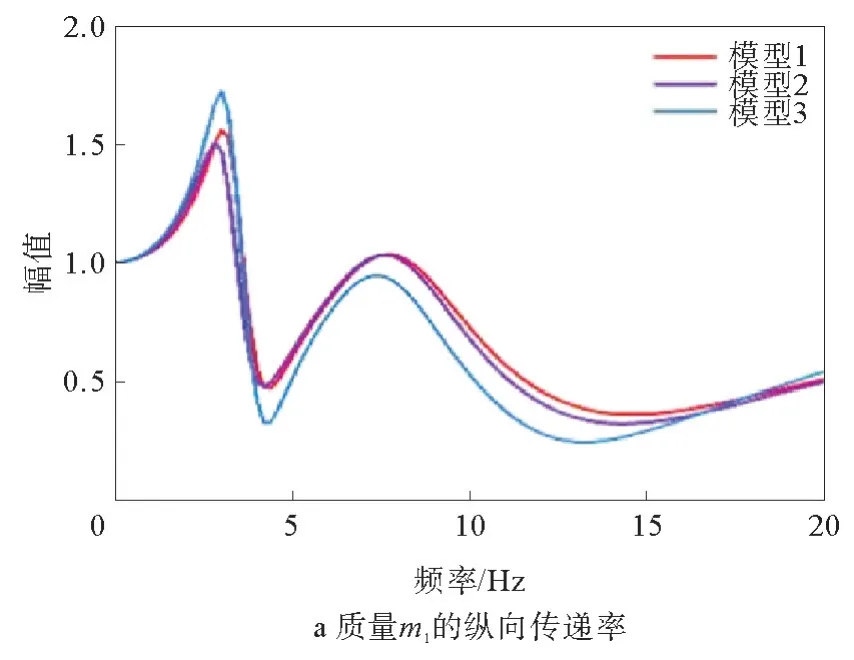
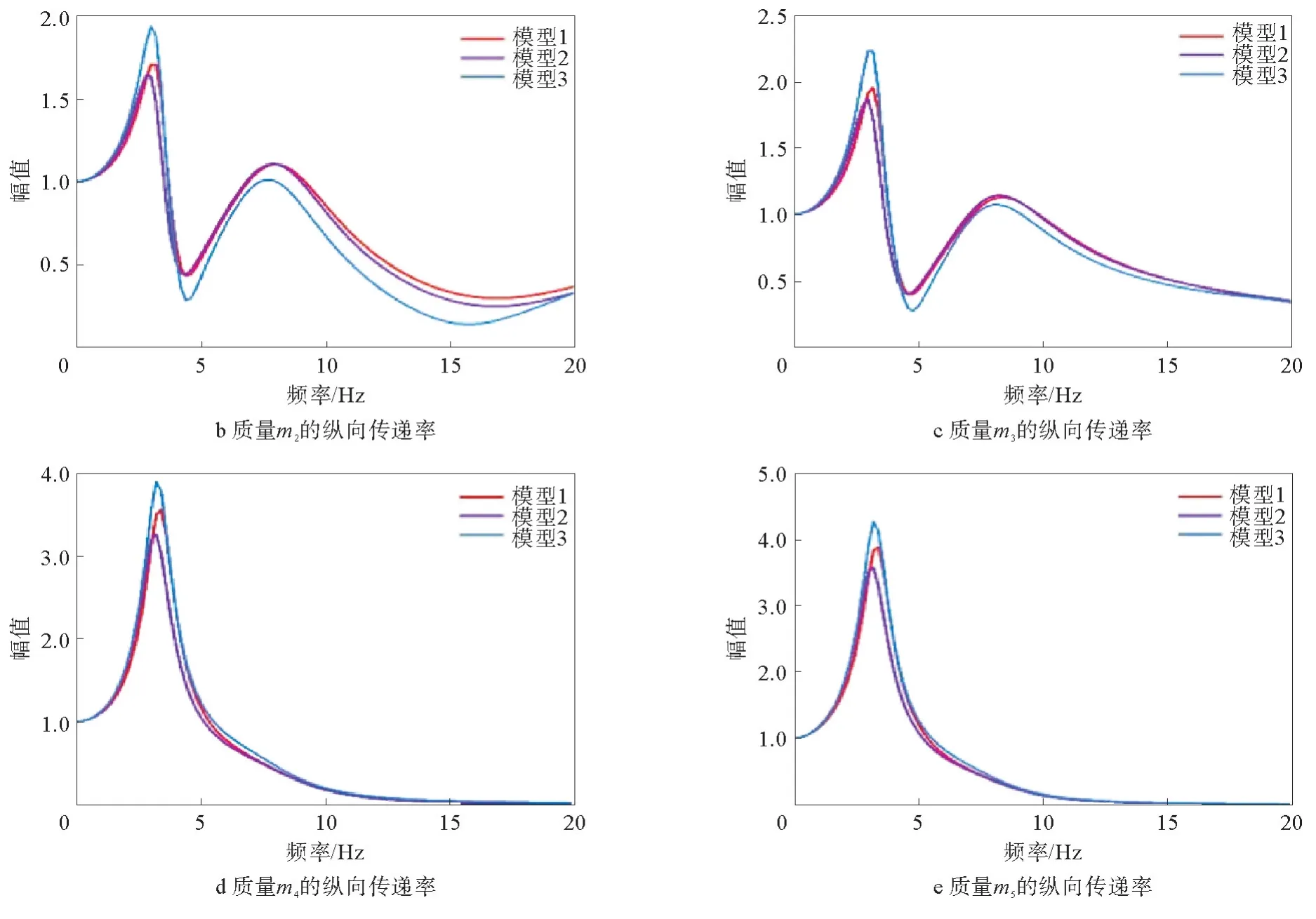
图5 人体各部位纵向传递率
由于座椅模型3的坐垫纵向刚度和阻尼系数较高,因此对人体各部位的传递率在共振频率处峰值都有所提高,但在高频率范围内对人体体段1~3的传递率却有所下降。因此,合适的坐垫和座椅悬架可以降低人体纵向传递率。
人体各部位侧向传递率如图6所示,图6a~图6e分别为人体部位1~5在3种座椅模型中的侧向振动传递率。
由图6可以看出,在侧向传递率中,由于水平方向对频率较敏感,因此3种座椅模型对人体各部位的共振频率都在1~4 Hz较小范围内。座椅模型1和座椅模型2对人体各部位传递率在峰值和共振频率上都没有显著变化,对比座椅模型3,增加了座椅悬架部分,不仅对人体各部位共振频率出现了降低趋势,还明显降低了体段4和5在共振频率处的峰值。
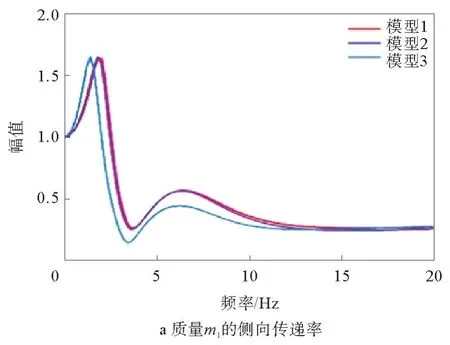
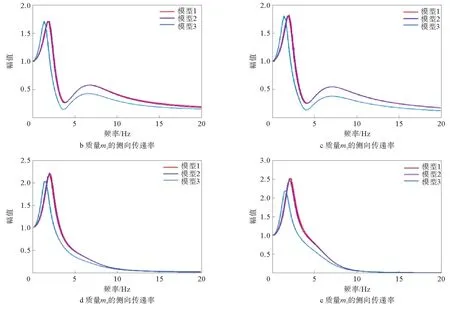
图6 人体各部位侧向传递率
人体各部位垂向传递率如图7所示,图7a~图7e分别为人体部位1~5在3种座椅模型中的纵向振动传递率。由图7可知,3种座椅模型对人体所有部位的共振频率均在3~8 Hz内,之后随着频率的增加而减小。座椅模型1中硬座对人体各部位的传递率最高,座椅模型2和模型3随着坐垫和靠背垫的增加,人体各部位在共振频率处的传递率峰值都有所下降,且共振频率出现降低的现象。因此,当地面给出激励频率时,通过选择合适的垫子及座椅刚度和阻尼系数,在该频率下可实现低传递率,以最小化对人体的振动传递,并最大化提高乘坐舒适性。
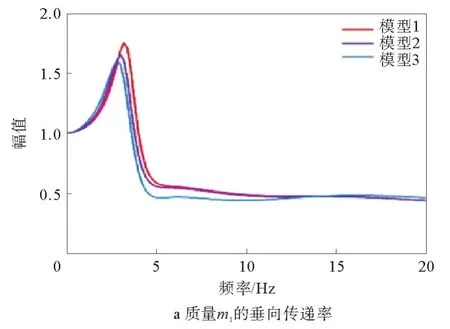
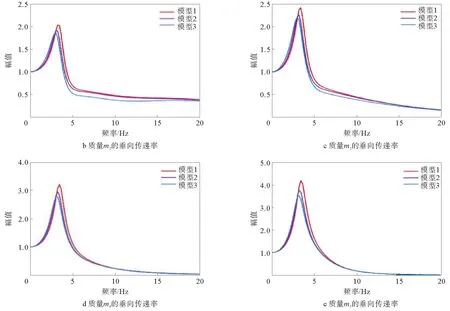
图7 人体各部位垂向传递率
5 结束语
本文通过建立三维坐姿动力学模型和3种不同座椅模型,即刚性座椅、带有坐垫的座椅、带有坐垫和座椅悬架的座椅,推导了人体各部位的运动方程表达式。以座椅到人体头部传递率为目标,通过振动试验,获取了人体头部在扫频激励下的振动传递率。采用遗传算法对头部传递率进行参数辨识,辨识出三维人体模型参数。将人体模型参数结合3种座椅模型进行对比分析,结果表明,第1种座椅模型在纵向和侧向的传递率幅值和共振频率都高于第2种和第3种座椅模型。第2种模型由于增加了坐垫和靠背垫,传递率幅值明显降低。第3种模型是隔振的最佳设置,不仅衰减了侧向和纵向的传振动,还降低侧向振动的共振频率。通过3种不同座椅模型的对比分析,说明增加坐垫和座椅悬架在很大的程度上可以提高乘客乘坐舒适性,该研究可用于座椅设计和人体振动响应预测。

