基于光节点模型的PRM 路径规划优化算法研究

韩 超杨 杰

(青岛大学机电工程学院,山东 青岛 266071)

近年来科学技术迅速发展,自主移动机器人的基础研究课题——机器人的路径规划获得了更广阔的发展空间,得到了更多学者的关注。它能够在有障碍物的环境下,于起始点和目标点之间生成一条无碰撞轨迹。在手术机器人[1]、智能汽车[2]、农业采摘[3]、船舶[4]等各个方面有广泛应用。目前常用的算法有A*算法[5-7]、快速随机搜索树算法[8--10]、概率路线图算法[11-13]人工势场法[14-15]、蚁群算法[16]等。其中,PRM 算法在多数情况下能用较少的采样点,规划出起始点至目标点的无碰撞轨迹。然而,仍存在无法通过狭窄区域,导致结果大幅偏离最优路径或规划失败的问题[17]。程谦等人[18]提出了一种基于连接点的优化方法,剔除算法在学习阶段构建的无效路径,使路径总数减少,缩短在查询阶段的搜索时间,有效地提高了PRM 算法的规划速度,但路径平滑度未改善,算法仍存在可能无解的问题;邹善席等人[19]引入随机节点生成函数和改进的节点增强法,减少了原始路径上节点数目,缩短路径长度,有效提高了路径平滑度,但引入随机节点生成函数并未改变在狭窄地图中可能无解的问题;谭建豪等人[20]提出将障碍物边界点作为PRM 算法的确定采样点,并在自由空间中构建最优可行区域,降低随机采样点的分散性,提高算法的时间和空间利用率,解决了在狭窄通道地图中可能无解的情况,但该算法运行时间增加,降低了运行效率。由此可知,上述研究无法同时解决路径平滑度低、在狭窄地图中可能无解、程序运行效率低的问题。针对这种情况,本文基于光照方法提出了一种优化PRM 算法,将起始点、目标点和采样的节点视为光源,提取未照亮范围并在其中进行采样,优化了采样方法,既减少了采样节点的数量,又解决了路径无解的问题,在狭窄直线通道地图具有良好的应用前景。

1 PRM 算法描述

1.1 学习阶段

PRM 算法是一种基于图搜索的方法,传统的PRM 算法分为学习和查询两个阶段。

学习阶段任务是构建无向网络路径图G＝(V,E),其中V代表节点集,E代表两节点之间的边集。首先,在整个地图中随机产生N个采样节点,保留在自由空间中的n个节点,构成路径图中的V;其次,将V中的每个节点与其邻居节点相连,并去除与障碍物碰撞的连线,构成路径图中的E。

1.2 查询阶段

查询阶段的任务是通过A*算法、深度优先搜索算法等搜索算法,在学习阶段构建的无向网络路径图中,找到一条连接起始点和目标点的无碰撞轨迹。传统PRM 算法为随机采样,存在采样点分布不均匀的情况,特别是在有狭窄通道的地图中,采样点会集中于空旷的自由空间,而在狭窄通道处不易产生采样点,容易出现路径无解的情况。

2 PRM 算法优化

为了解决传统PRM 算法路径平滑度低、在狭窄地图中可能无解、程序运行效率低的问题,优化后的采样方法将采样节点视为光源,在未照亮区域进行采样,可以减少采样节点的数量。

2.1 光照区域获取

将起始点Ps与目标点Pg视为两个光源,获取Ps和Pg的光照区域。光照区域获取过程如图1所示。由图1a可以看出,地图中的障碍物为黑色,以起始点Ps为光源中心,向周围360°释放射线。由图1b可以看出,沿着以光源为起点的射线,间隔相同步长多次取点,直至找到射线与障碍物碰撞的所有点,将这些点存储为多边形的顶点,构成表示光照区域的多边形。

图1 光照区域获取过程

获取光照区域的伪代码如下:

2.2 节点采样

光照区域为灰色部分,光照节点采样过程如图2所示。由图2a可以看出,将光照区域分别存储为多边形,并将其添加到多边形列表中。

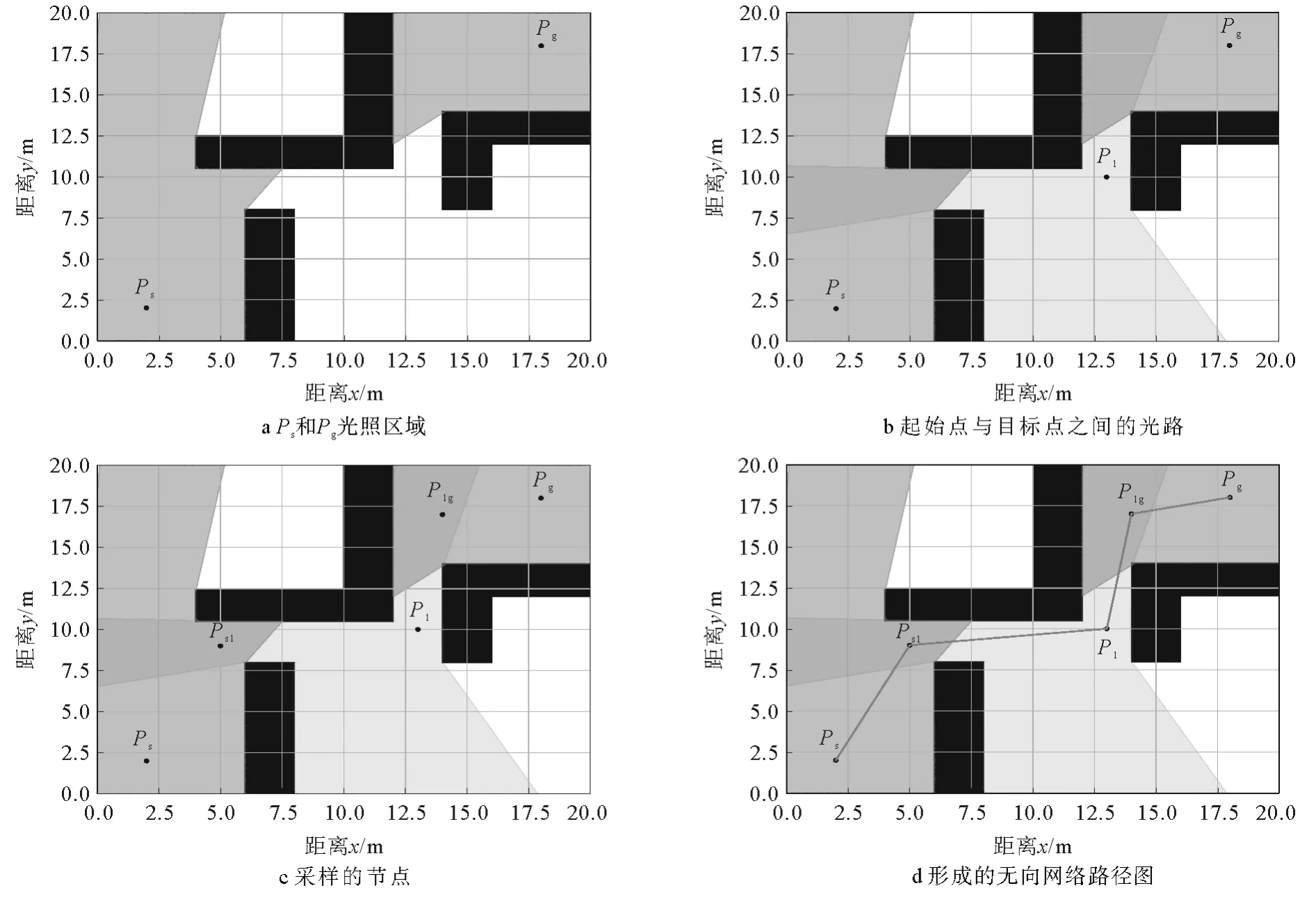
图2 光照节点采样过程

若多边形列表中所有多边形存在连接起始点与目标点的光路,则找到连通Ps和Pg的轨迹;若未找到,则在未照亮的自由区域进行采样,得到节点P1,并将P1的光照范围存储为新的多边形。重复上述步骤,将新的多边形添加到多边形列表中,继续检测多边形列表中所有元素构成的多边形是否存在连接起始点与目标点的光路,若不存在则继续采样,直至照亮的区域能够连通起始点与目标点。由图2b可以看出,构成起始点与目标点之间的光路,通过该方式采样得到的节点只会出现在未照亮区域,同时节点数量大幅减少,继而提升了路径平滑度、提高了程序运行效率。

由图2c可以看出,在多边形列表中光照范围的重合部分继续进行节点采样,得到Ps1和P1g。将Ps、Pg以及所有采样点作为节点,将所有光照范围有交集的节点两两连接,作为无向网络路径图的边。由图2d可以看出,将两个节点之间的欧氏距离作为对应边的代价值,形成的无向网络路径。构建无向网络路径图的流程如图3所示。

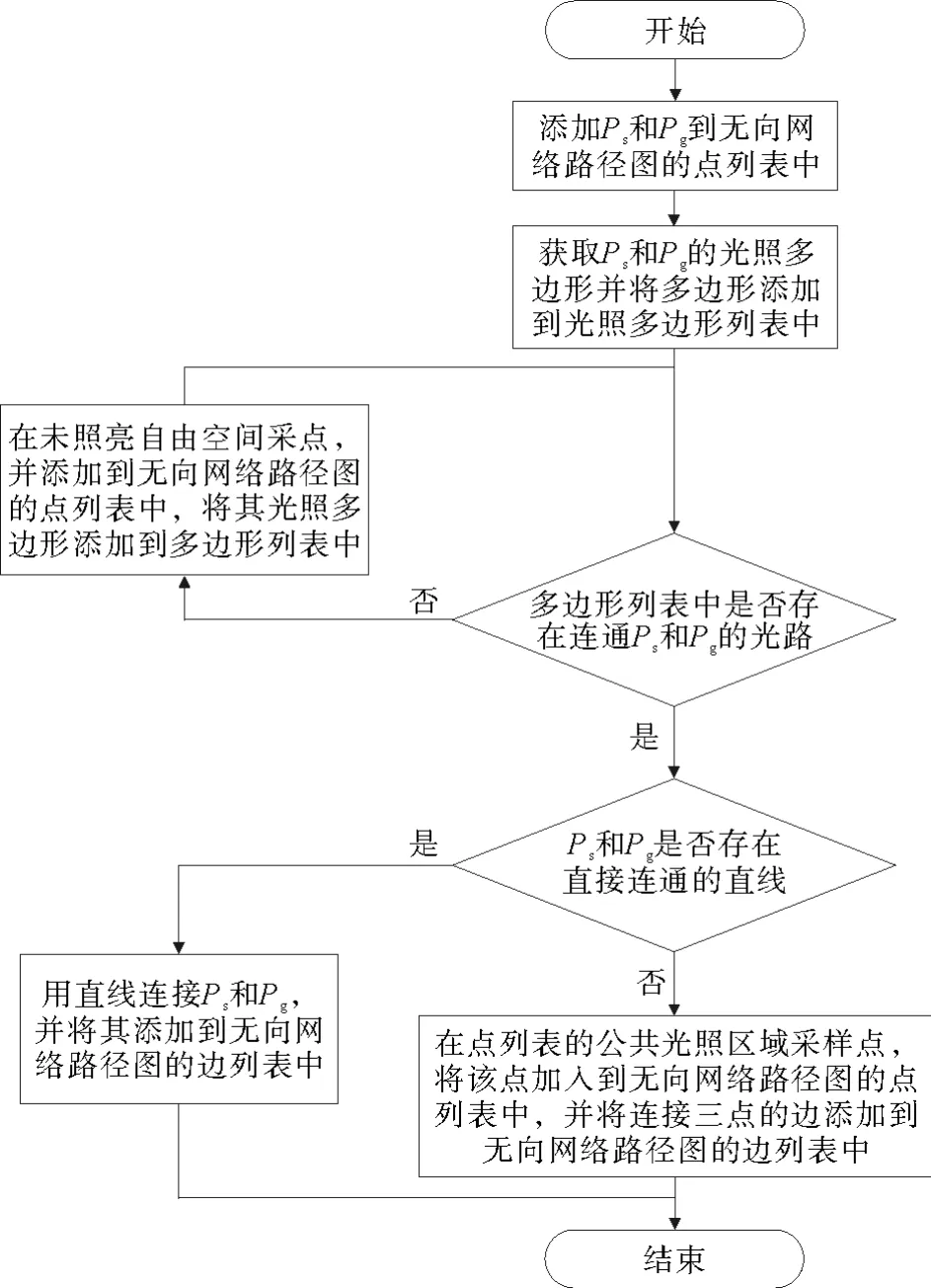
图3 构建无向网络路径图的流程

2.3 选择无向图中最优路径

在上一步生成的无向网络路径图中,使用Dijkstra算法获取无向有权图中Ps至Pg的最短路径。最后优化路径,遍历路径中的所有节点,尝试依次删除每个节点,并将所删除节点前后的两个节点相连,生成无向有权图的边。若新添加的边未与障碍物发生碰撞,则更新路径,获取相对更短路径。

3 优化算法仿真结果及分析

3.1 单个狭窄通道地图仿真

为了测试优化PRM 算法的性能,本文将其与传统PRM 算法进行测试对比。电脑处理器为Intel Core i5-7200U,主频2.50 GHz,内存8 GB。

单个狭窄通道地图大小为20 m×20 m,起点位置设置为(4,10),终点位置设置为(2,1)。将传统PRM算法依次取300,500和1 000个采样节点,在每组节点数进行50次实验的基础上,与优化PRM 算法进行对比,并取优化PRM 算法的射线数量和射线步长分别为36和0.5 m。实验生成无向网络路径图和最终路径,单个狭窄通道地图仿真实验对比如图4所示。

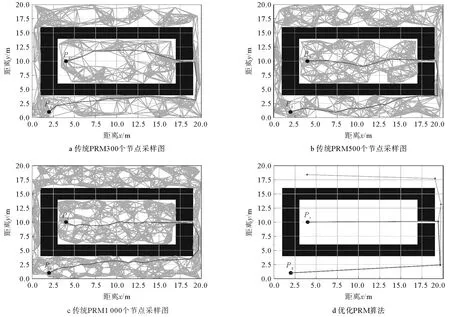
图4 单个狭窄通道地图仿真实验对比

单个狭窄通道地图仿真50次实验数据对比如表1所示,实验结果表明,采样节点数分别为300,500和1 000个的传统PRM 算法与优化PRM 算法,能够规划出无碰撞路径的概率分别为68%,72%,96%和100%。相较于这3种条件下的传统PRM 算法,优化PRM 算法的规划平均时间分别降低58.97%,72.49%和88.38%;平均路径平滑度使用路径转角之和量化,分别提升60.35%,68.35%和77.11%;平均路径长度基本保持不变。

表1 单个狭窄通道地图仿真50次实验数据对比

3.2 多个狭窄通道地图仿真

多个狭窄通道地图大小为20 m×20 m,起点位置设置为(1,1),终点位置设置为(19,19)。将传统PRM算法依次取500,1 000和2 000个采样节点,在每组节点数进行100次实验的基础上,与优化PRM 算法进行对比,并取优化PRM 算法的射线数量和射线步长分别为36和0.5 m。实验生成无向网络路径图和最终路径,单个狭窄通道地图仿真实验对比如图5所示。

图5 多个狭窄通道地图仿真实验对比

多个狭窄通道地图仿真100次实验数据对比如表2所示,实验结果表明,采样节点数分别为500,1 000和2 000个的传统PRM 算法与优化PRM 算法能够规划出无碰撞路径的概率分别为14%,52%,96%和100%。与这3种条件下的传统PRM 算法相比,优化PRM 算法的规划平均时间分别降低50.49%,66.57%和83.14%;平均路径平滑度分别提升42.81%,54.57%和64.62%;平均路径长度基本保持不变。

表2 多个狭窄通道地图仿真100次实验数据对比

4 结束语

本文基于传统PRM 算法,加入光照采样节点的方法,提出了一种优化PRM 算法,可应用于狭窄直线通道地图。该算法不会在光照范围内采样,不仅减少了采样节点数量,而且提高了采样节点利用率,在路径长度基本保持不变的情况下,缩短了路径规划时间。与目前广泛采用的改变随机节点生成函数的方法相比,优化后的PRM 算法路径节点大幅减少,因而提高了路径平滑度,同时具有完备性,极大地提高了运行效率。仿真实验已经证明了优化PRM 算法的可行性。但是,该算法的适用场合仅限于狭窄直线通道地图,而在普通地图和环形狭窄通道地图中的仿真实验效果有待提升,因此建议后续研究将本文算法与其他算法相结合,提出适用于多种地图的新算法。