自发渗吸时间标度归一化处理方法
魏 兵 ,李沁芷,刘成钢
1.油气藏地质及开发工程国家重点实验室·西南石油大学,四川 成都610500 2.中国石油川庆钻探工程有限公司,四川 成都 610000
引言
随着油气开采的不断深入,非常规油气已成为石油开采的一个新方向。中国致密油资源量丰富,分布范围广,并已在鄂尔多斯、松辽、准噶尔(含三塘湖)和渤海湾4 个陆相盆地获重大发现。中国致密油地质资源量约为200×108t,技术可采资源量可达(20~25)×108t,是接替常规油气资源支撑中国能源自给的重要力量[1-2]。水平井多级压裂是当前国内外致密油开发的主体技术,该技术虽然解决了储层初期产量的问题,但地层能量衰竭快、单井产量递减迅速,尤其在中国几个典型的陆相致密油藏,长期处于低产、低效状态,预测采收率普遍偏低,仅为2%~5%[3-5],亟待优选开发方式,提高原油采收率,实现资源效益动用。
致密储层压裂改造后形成复杂缝网,Thomas等[6]指出在改造区内裂缝是流体流动的主要通道,控制着注入流体的波及范围,而裂缝和基质间的物质交换是提高基质动用程度和原油采收率的关键,这种物质交换可通过流体-流体、流体-岩石之间的相互作用实现[7]。自发渗吸是油田开发中一种典型的物质交换过程,近年来在致密储层提高采收率中引起广泛关注。大量的室内研究表明,水、表面活性剂、纳米颗粒等流体在渗吸作用下进入基质内部,将原油从基质中置换出来[8-9]。但由于室内实验岩芯模型简单、尺度小、时间短等现实问题,导致室内结果无法直接应用于油藏尺度渗吸效果分析、评价和预测。通过将室内实验结果无因次化,建立考虑不同渗吸条件的时间标度无因次模型,可有效解决尺度不一致的问题。为拓宽和深化自发渗吸在致密油藏提高采收率上的应用,笔者详细梳理了近年来国内外有关渗吸过程时间标度。
1 自发渗吸主要原理和规律
自发渗吸是指在多孔介质中,湿相在毛管力作用下置换非湿相的过程[10]。根据流体流动方向,可以分成同向渗吸(co-current imbibition)与逆向渗吸(counter-current imbibition)。图1 为同向渗吸和逆向渗吸示意图。同向渗吸是指湿相和非湿相在同一方向上运动,逆向渗吸是指湿相和非湿相在相反方向上运动。两者的主要区别是:(1)相之间的黏性耦合可能意味着同向渗吸过程的相对渗透率将高于逆向渗吸;(2)在逆向渗吸时,非湿相必须从湿相入口离开[11-13]。
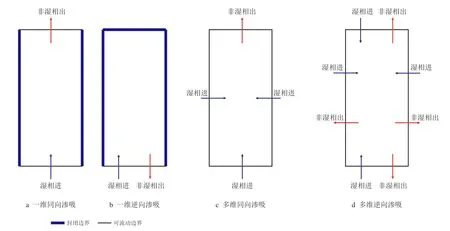
图1 同向渗吸和逆向渗吸示意图Fig.1 Schematic representation of co-current and counter-current imbibition
在裂缝性油藏中,逆向渗吸往往与同向渗吸同时发生。对于多维情况,自发渗吸的研究更加复杂。大量国内外实验证实,同向自发渗吸的最终采收率远高于逆向自发渗吸[14]。
Washburn[15]用一根毛细管首次进行了自发渗吸(水置换空气)的概念验证实验,在忽略空气黏度的前提下,提出了一个空气和水之间弯液面运动的计算模型,证明了湿相移动的距离与时间的平方根成比例。随后,该模型被Morrow 等[16]扩展到当毛细管内部流体具有黏度,而侵入流体的黏度忽略不计(即气体)的情况下,流体流动的主要驱动力为毛管力,此时毛管力与湿相黏滞阻力(viscous resistance)均与气体侵入长度成正比。进一步推广到侵入流体具有黏度的情况下,当非湿相流动受到侵入的湿相流动的限制时,湿相移动的距离与时间的平方根相关。这为推导自发渗吸的无因次方程和建立渗吸数值模型提供参考。
自发渗吸的理论基础为毛管力方程。假定半径为r的理想毛细管,湿相与非湿相的界面张力为σ,则毛管力为

假定流动为层流,用Poiseuille 方程描述毛细管内的层流,则平均速度为

假定主要驱动力为毛管力,速度为v=dx/dt,对方程进行积分

流度比M=μd/μ,即湿相(侵入流体)黏度与非湿相黏度之比,则有[17]
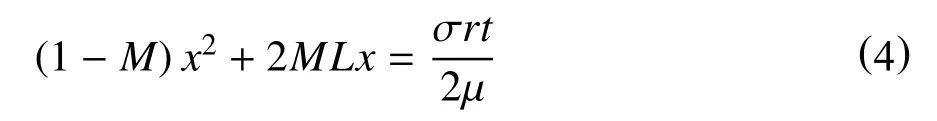
许多学者为模拟多孔介质中的自发渗吸作用,分析了相互连接的毛细管中的渗吸,确认了在较小半径的孔隙中湿相有较大的毛管力驱动,界面运移速度更快[18-20]。Unsal 等[21]利用实验手段及理论分析研究了具有非对称几何结构介质中的渗吸作用,指出只有当非湿相背压超过阈值时,逆向渗吸才可能发生。由于毛细管形状的不规则性以及渗吸入口端同向与逆向渗吸同时发生的复杂性,目前,并无解析方法描述此过程。多孔介质中基质-裂缝的传质扩散规律十分复杂,目前,裂缝性油藏中自发渗吸的流体交换机制及作用规律并不明确,找到能适应天然多孔介质复杂结构的数学模型和解析方法十分重要。
原始地层条件下油水界面张力较高,自发渗吸主要由毛管力控制。但在化学剂介入条件下,例如向储层中注入表面活性剂等物质,油水界面张力降低,逆向渗吸转变为同向渗吸,重力的贡献逐渐升高。Schechter 等[22]指出,重力和毛管力影响湿相自发渗吸的程度可以通过邦德数NB的倒数进行解释和估算

当研究对象为毛细管模型时,C1为0.4。当>5.0 时,湿相的自发渗吸主要由毛管力决定,当0.2≤≤5.0 时,湿相的自发渗吸由毛管力和重力共同决定,当<0.2 时,湿相的自发渗吸主要由重力决定。随着岩石表面亲水性增加,毛管力会增加,会增大。同时,这也说明界面张力越低,重力作用越明显[23]。
许多学者证实,润湿性对渗吸过程的影响不可忽略[24-25]。对于多孔介质,润湿性将控制毛管力的大小与方向,则有

式(6)可用于定性评估润湿性改变过程中毛管力与重力的相对影响。毛管力和重力控制机制将直接影响自发渗吸过程的渗吸速度和最终采收率,探究不同作用机制下的无因次时间与采出程度的关系,有助于建立相关的分析模型进行标度扩展,以此分析、评价实验室模型是否能够应用于实际油藏。
国内外学者就此开展了渗吸时间标度研究,建立和修正标度评价模型,研究不同渗吸介质作用下的控制机制、修正后时间标度的限制性及归一化能力,提出了适用于致密储层渗吸过程中的无因次时间修正模型,并结合实际油藏情况,进行校正和进一步研究。
2 渗吸时间标度归一化处理
许多学者研究了自发渗吸的无因次处理方法,比较界面张力、流体黏度、岩石孔隙度与渗透率、岩芯几何形状以及边界条件等对渗吸效率的影响,并在此基础上对渗吸采收率与时间进行归一化处理,将不同的实验结果放在同一标度下进行比较。Mattax 等[26]基于Rapoport[27]的数值解,提出了毛管力渗吸驱油关系式及无因次时间方程(MK模型)

式(8)是Mattax[26]提出的无因次时间,但该式只在满足以下条件才能使用:(1)重力的影响可忽略;(2)油水相黏度具有可替换的相关性;(3)岩样在边界条件和形状上相同;(4)相对渗透率曲线相同;(5)毛管力函数必须正比于界面张力;(6)基质中初始流体分布相同。条件(4)~(6)表明了该模型要求岩样需满足润湿性一致且孔隙结构相似。模型的限制性过强,适用范围窄,对于非常规油藏适用性差。
Cuiec 等[28]提出了对Mattax[26]无因次时间方程的修正,得到了更好的拟合效果,将原油黏度代替水的黏度。另外,Zhang 等[29]重新定义了黏度相,将油水两相黏度的几何平均值取代了单一黏度相,在Cuiec 等[28]的基础上对Mattax[26]无因次时间方程进行修正
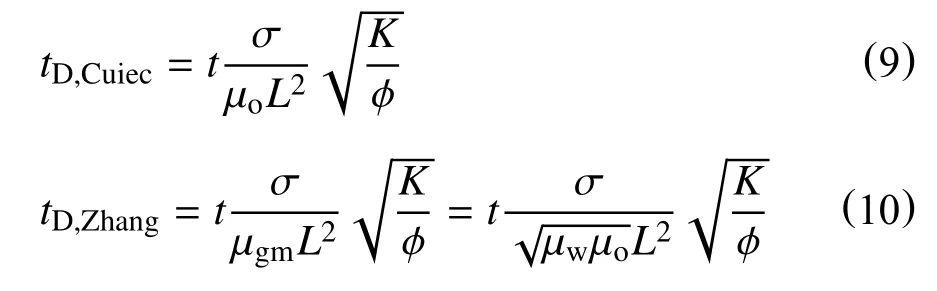
研究发现,不同几何形状的岩芯采用同一标度方程未能体现良好的一致性,最初进行的实验室岩芯自发渗吸研究并未考虑岩芯形状和边界条件的影响。为了将这一影响因素纳入考虑,Kazemi 等[30]引入了一个形状因子Fs,同时定义无因次时间方程中的特征长度

Ma 等[31]指出上述特征长度不能应用到只有一面开启的逆向自发渗吸,并提出了一种修正方法,为衡量不同油、地层水及基质条件下的渗吸情况,用于修正渗吸前缘到无流动边界的移动距离,只有逆向渗吸情况下,才有所不同。对于逆向渗吸情况下特征长度表示为
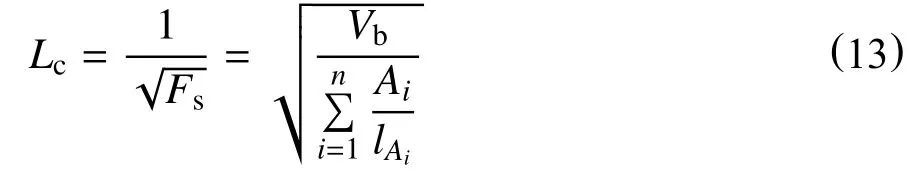
基于先前的无因次时间方程,Ma 等[31]同时提出引入特征长度后的标度方程。式(14)同时考虑水、油黏度,可用于不同的边界条件设计,作为典型的致密油藏自发渗吸经验标度方程

Ma 等[31]提出的方程主要应用于黏度在1~172 mPa·s 的矿物油和黏度为1 mPa·s 的水相,通过关联以往的现场数据和Berea 砂岩的渗吸结果,考虑了岩芯大小、形状以及边界条件和黏度比的影响,证实了曲线良好的归一性。Li 等[32]采用玻璃珠填充圆管的多孔介质模型模拟了气水两相的渗吸实验,引入了含水饱和度参数,并验证了该标度模型的准确性。Fischer 等[33]提出放大黏度研究范围,发现Ma 等[31]的无因次时间方程不适用于油水黏度比增大的情况。Ma 等[31]提出的模型仅适用于流体黏度比会影响油水相有效渗透率的情况,而一些自发渗吸模型中两相有效渗透率并不依赖于流体黏度比,因此,Mason 等[34]引入一个新的黏度标度因子,并提出了一个新的经验相关无因次时间方程
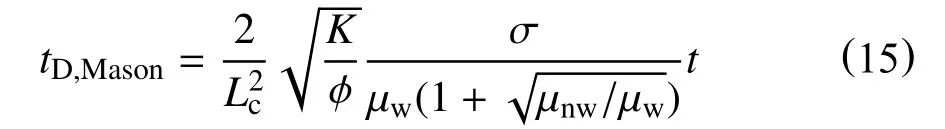
Mason 等[34]提出的方程与Ma 等[31]的方程均同时考虑了多孔介质的界面张力、流体黏度、岩芯形状、孔渗结构以及边界条件,其主要区别在于分母的黏度项有所不同。该模型扩宽了渗吸过程中油水两相黏度比的适用范围。研究发现,当水相黏度高时,无因次时间主要由水相决定。
因此,前者能更多地应用于超强水湿和强水湿环境,但对于混合润湿和中性润湿的岩石而言,Ma 等[31]的无因次方程,原油采收率与无因次时间的关系曲线表明其具有较好归一性。无因次时间模型也可以推导出归一化采收率模型,对于精准地预测最终采收率起到关键作用。
表1 中列举了不同学者提出的渗吸无因次时间方法,对于近些年不同作用机制的渗吸时间标度方法会在后面部分详细说明。

表1 无因次时间方法归纳Tab.1 Summary of dimensionless time methods
3 不同作用机制渗吸时间标度归一化处理方法
自发渗吸主要由毛管力、重力和黏滞力3 种机制决定。黏滞力影响较小,在标度处理过程中往往是作为无因次时间模型中黏度相进行考虑和修正。致密储层渗吸由于孔隙半径小、结构复杂,毛管力作用非常显著,在无外部作用的情况下重力的影响比较小。但是当具有表面活性的物质介入时,油水界面张力下降,根据毛管数NC和邦德数NB,此时重力的影响不可忽略。笔者根据渗吸时间标度归一化处理方法,将渗吸作用机制分为毛管力主导、重力主导以及二者共同控制3 种情况(图2)。
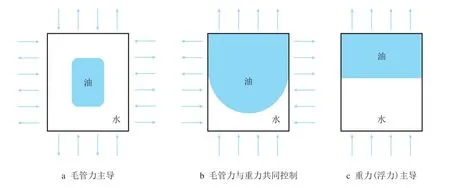
图2 自发渗吸时油水两相分布图Fig.2 Distribution of oil and water inside cores
3.1 毛管力主导自发渗吸
裂缝性油藏基质原油启动取决于基质-裂缝间传质扩散作用。如果岩石表面是水湿(亲水油藏),且裂缝中含水量高,自发渗吸主要靠毛管力作用。基质渗透率、大小和形状、润湿性、非均质性以及边界条件等共同决定了渗吸效果[38-40],同时湿相的性质、黏度以及界面张力等对毛管力渗吸提高采收率也有较大影响。在渗吸早期,湿相流体开始进入基质,毛管力为渗吸的主要驱动力。前文提到,Mattax[26]在Rapoport[27]的数值解基础上首先提出了渗吸时间标度方程并随后进行了修正。然而,Babadagli[41]指出在时间标度设计中,润湿性的影响往往被忽略,基于Handy[42]实验,渗吸的流量Q和渗吸时间t之间存在以下关系
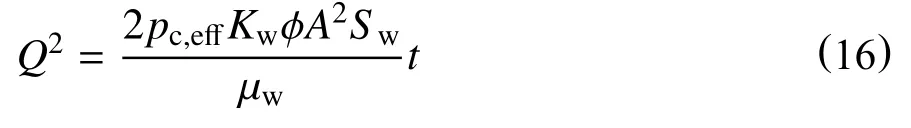
国外学者已证实,湿相的运动距离与时间的平方根正相关。基于此结论,Ma 等[43]针对式(16)提出将渗吸采收率与时间平方根进行相关,则会得到一条直线

c*即为描述采收率和时间平方根的简化参数,由式(16)变形得到,c*包括界面张力、润湿性和孔径,因此,斜率c*就可以用来表征特定岩石流体系统的渗吸能力。毛管力渗吸速率也受原油黏度的控制,因此,直线斜率不仅是毛管性质的函数,也是原油黏度的函数。Babadagli[41]针对同向渗吸将斜率进行标准化处理,修正了Ma 等[31]提出的无因次时间方程
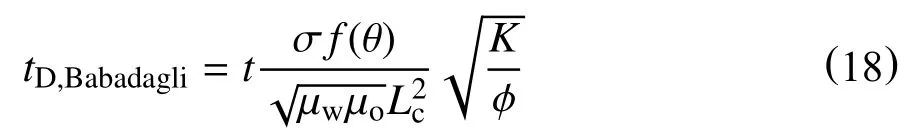
Babadagli[41]提出的修正无因次时间方程能够很好地消除采收实验数据的分散性。然而,对于逆向渗吸情况,式(18)不能得到归一化曲线。如果只考虑毛管力的影响,忽略重力影响,往往需要考虑特殊的边界条件。Mirzaei 等[44]提出了一维同向自发渗吸的无因次时间标度方程,同时简化得到了不含毛管力和相对渗透率参数的一维同向渗吸无因次时间方程
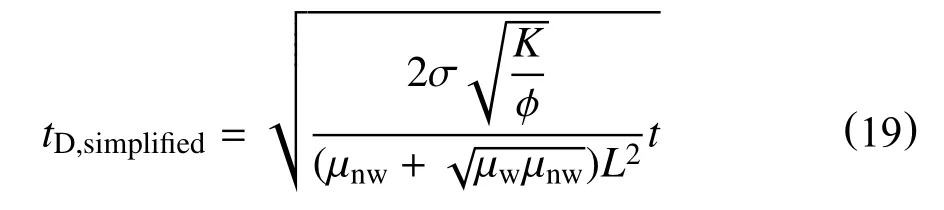
通过拟合采出程度与无因次时间关系,可以观察到数据的分散性明显降低,曲线将所有数据归一化到一个狭窄的区域。对于多维同向自发渗吸,Mirzaei 等[44]设计了不同的边界条件,基于先前国内外学者提出的不同边界条件渗吸的数值模型,引入了一个多维同向自发渗吸形状因子,修正后同样得到了一个简单的标度模型
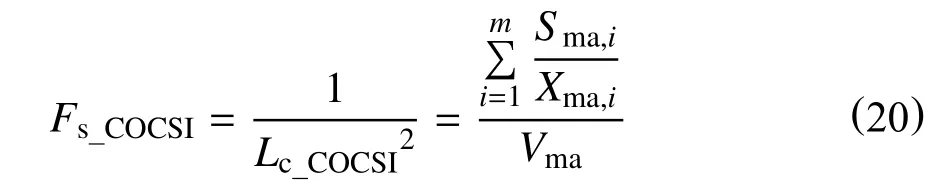

对于毛管力主导的逆向自发渗吸也进行了非常多的研究,许多学者指出,逆流渗吸在天然裂缝发育的油藏中极大促进了基质与裂缝间流体的交换过程。文献[45-47]指出,若毛管力是渗吸的主要动力,孔隙中的湿相与非湿相流体沿相反方向运动,此时逆向自发渗吸为主;若重力是渗吸的主要动力,湿相与非湿相则沿相同的方向运动,此时同向自发渗吸为主。渗吸作用的研究方法主要有解析法、数值法和物理模拟实验法[48]。对于致密储层自发渗吸规律的数值研究,是在无因次J函数[49]以及水-油流动模型“相似准则”[27]理论基础上进行。Mcwhorter 等[50]首次提出了自发渗吸的半解析解,但由于忽略了入口端边界条件,解析解的应用性较差。Kashchiev 等[51]以及Schmid 等[52]前后提出相关修正的解析解。前者为毛细管力和相对渗透率的限制性函数形式,后者指出McWhorter 等[50]的方程只适用于逆向渗吸条件,并求解得到了一个隐式非线性二阶常微分方程,但求解难度大,需要迭代求解一个常数C。Alyafei 等[53]发现,通过反向差分法以及迭代过程可以得到最终解。此外,还可以通过将解析解简单的变量操作,得到Schmid 和Geiger[54]公式的扩展形式,通过求解湿相的前缘端运动,进一步得到无因次时间与特征长度的方程。此时修正的无因次时间定义为[55]

半解析解的研究同时拓展到了数值模型方面,Khan 等[56]使用全隐式黑油模型模拟了自发渗吸过程。网格基于角点法,采用经典的有限差分格式,同时设置强水湿、弱水湿和混合润湿3 种润湿情况模拟逆向自发渗吸。结果表明,数值解和半解析解匹配性好。因此,式(22)在毛管力主导的逆向自发渗吸得以广泛应用。对于仅考虑毛管力的情况,渗吸的控制机制较单一,已有较完善的时间标度归一化处理方法和模型。但对于孔隙结构复杂的致密储层,毛管力主导的时间标度公式并不能实现实际油藏渗吸数据归一化,在自发渗吸过程中,重力的影响不能忽略,弄清重力对渗吸的影响非常关键。
3.2 重力主导自发渗吸
对于高渗透储层,重力的影响通常比较大甚至可能忽略毛管力影响。但对致密储层,重力引起的自发渗吸需要在湿相中加入表面活性物质,通过降低界面张力或改变润湿性改变NB[57],特别是表面活性剂、微乳液等高活性物质,会形成超低油水界面张力,所以毛管力忽略不计。采用NB进行判断,当<0.2 后,重力主导渗吸,基质原油通过浮力渗出。
重力是否能成为致密储层自发渗吸的主要驱动力取决于油水界面张力。Ravari 等[58]研究了表面活性剂增强重力排水及改变润湿性对原油采收率的影响。在高渗储层中观察到3 种作用,即润湿性变化提高的采收率、毛管力和重力联合作用提高的采收率、重力作用提高的采收率。重力在自发渗吸提高采收率中的作用随界面张力的降低而显著增加。
Parson 等[38]首次提出了低界面张力下重力作用渗吸无因次时间

Cuiec 等[28]对式(23)修正并类比毛管力渗吸无因次模型,发现用μo取代μw能更好地拟合曲线,修正后的模型可以用于不同类型油藏重力主导渗吸过程。

Babadagli[41]将修正后的方程应用在采出程度与无因次时间的关系中,证实对于表面活性剂溶液-油体系的同向渗吸能够较好地消除数据的分散性,对于致密储层表面活性剂渗吸,还需考虑表面活性剂溶液-油体系存在额外边界层效应,特别是在微纳米尺度孔喉中,边界层现象非常明显。边界层是多孔介质孔壁上形成的一层不可动的润湿性流体,流体在渗吸时真实的流动半径小于储层的喉道半径[59-60]。表面活性剂溶液-油体系与盐水-油体系不同,引入特征长度并不能消除边界层效应。为了减小误差,Babadagli[41]在Cuiec 等[28]的研究基础上,提出引入一个边界条件因子(BCF)

把修正后的无因次模型用于不同边界条件同向渗吸并与Cuiec 等[28]提出的重力无因次时间模型对比,优化了拟合效果,消除了渗吸数据的分散性。边界条件的影响导致了渗吸作用机理及重力和毛管力对原油采收率相对贡献的变化。另外,Jacquin等[61]提出另一种方法,以黏滞力和重力比计算参考时间,重力主导渗吸的无因次时间表达式为
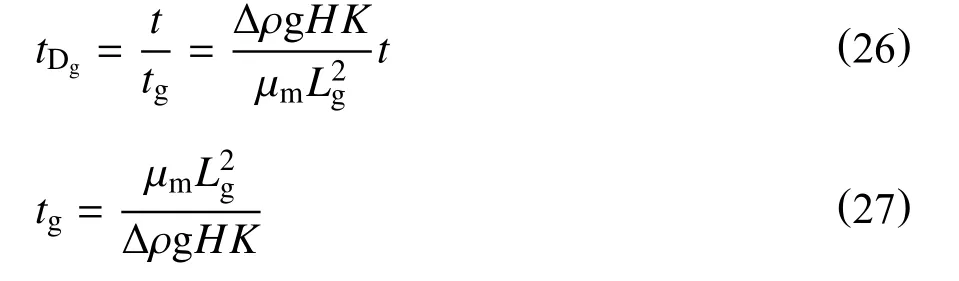
对于垂直和横向水平放置的岩芯,Lg等于L,H等于岩芯直径。致密储层渗吸过程中,随着时间的增加,渗吸逐渐过渡到中期阶段,渗吸过程可能是由毛管力和重力共同控制[41,62-64]。
3.3 毛管力和重力共同控制自发渗吸
如上所述,根据邦德数NB定义,当0.2≤≤5.0 时,湿相自发渗吸由毛管力和重力共同决定。对于致密储层,原始状态下毛管力是自发渗吸的主要动力。随着界面张力降低,毛管力的影响逐渐降低,重力作用愈发显著。也有学者指出,渗吸的方向也会决定重力的效果。对于垂直岩芯,重力作用的提高采收率效果远大于水平岩芯。Alsherhri等[65]采用CT 对比了水平和垂直放置岩芯的渗吸排油效率,研究发现不论是水还是表面活性剂垂直渗吸的采收率高于水平渗吸。
通过降低油水界面张力,能够提高基质原油的流动能力。毛管数综合了黏滞力和毛管力能很好解释原油采收率和油水固性质的关系。对于低界面张力环境重力和毛管力共同控制的渗吸,黏性驱动也会造成一定影响,裂缝中的压力梯度会提高黏性驱油效率。黏性驱动的时间标度归一化方法中,Standnes[37]提出了含有黏度指数Ve的黏度标度项(取值为0~1),引入无因次时间模型中并验证了该模型的准确性。
对于毛管力和重力共同控制的自发渗吸时间标度,通常是将两者的无因次时间模型结合起来,分析采出程度与无因次时间相关曲线与实验数据的拟合程度。Babadagli[41]结合修正模型式(18)和式(25)研究了表面活性剂-油体系实验的归一化情况。实验证明,引入一个边界因子后数据的分散性降低,同向渗吸过程无因次时间归一化程度高。Akin等[66]研究发现,自发渗吸过程中,油水前缘的运动为活塞式推进。周林波等[62]在Akin 等[66]基础上建立渗吸速度表征模型,同时考虑含水饱和度的变化,提出了同时含重力和毛管力的时间标度模型
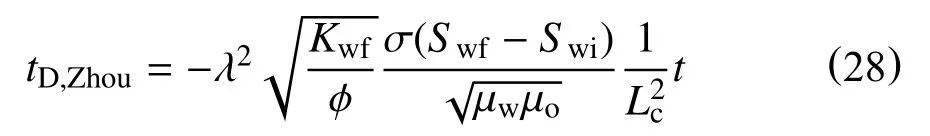
Bourbiaux 等[63]将Ma 等[36]建立的毛管力渗吸的无因次时间模型[式(14)]和Jacquin 等[61]建立的重力渗吸的无因次时间模型[式(26)]结合,研究了添加润湿改进剂后油湿碳酸盐岩油藏渗吸提高采收率效果。Li 等[64]研究了在低界面张力环境中表面活性剂渗吸的时间标度模型,此时浮力的驱动作用增强,提出了毛管力和重力耦合无因次模型

Li 等[64]在无因次模型的基础上建立了圆柱形和长方体岩芯的解析模型。
4 带压渗吸时间标度归一化处理方法
对于致密储层,焖井是提高自发渗吸效率的关键阶段[67],在此阶段渗吸一般是在带压条件下实现。国内外已有类似实验研究和相关报道,朱维耀等[68]采用NMR 研究了重水驱替下的渗吸过程,驱替作用主要发生在注水早期,即使后期渗吸逐渐占据主导地位,但驱替作用对原油采收率的影响不可忽略。
Jiang 等[69]结合Mason 无因次时间模型[34]与Leverett 毛管力函数[49]开展了带压条件下渗吸时间标度归一化研究。根据NMR 测得T2谱图,加权计算求解得到平均孔隙半径,将孔隙半径作为围压的函数进行拟合

将Leverett 毛管力函数[49]引入Mason 模型[34]
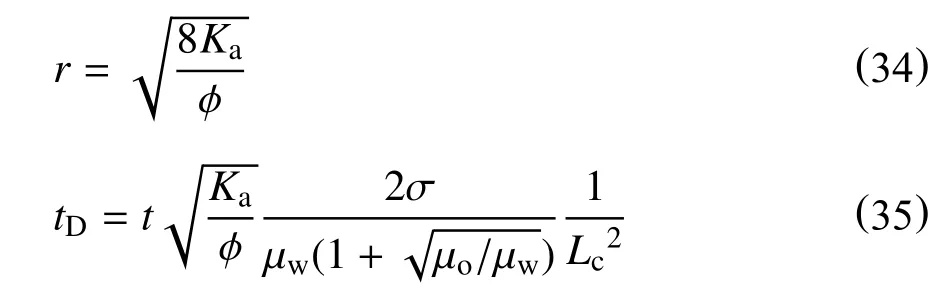
对于全开放型岩芯,其特征长度Lc为


将式(37)代入式(35)中,得到带压渗吸的无因次时间模型,简化可得
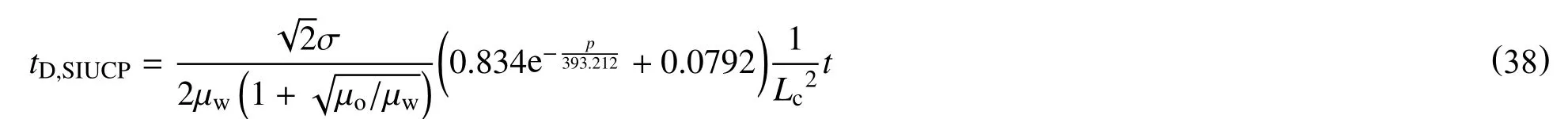

Xu 等[70]将带压渗吸无因次模型应用于采出程度与无因次时间的曲线中,与修正前的Mason 模型[34]比较,修正模型缩小了无因次时间范围,归一化效果较好。
为优化焖井时间,使用修正的无因次时间模型将实验室与现场数试验数据联系

油藏焖井时间为
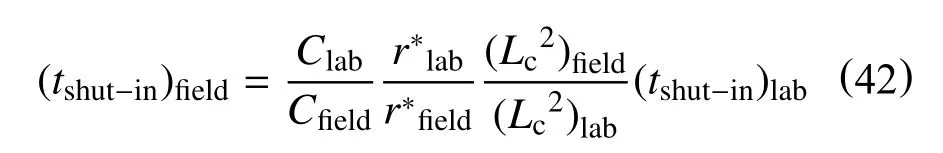
Xu 等[70]也指出,由于是在带压条件下进行的渗吸实验,采出程度不仅与自发渗吸作用相关,也和压力相关。对于带压渗吸的时间标度归一化方法研究,压实的作用还未得到相应的证实。
5 结论
(1)渗吸作用是致密储层注水、表面活性剂等提高采收率重要机理之一,归一化处理能在一定程度上将实验室无因次模型拓展至实际油藏应用,分析和预测渗吸提高采收率效果。
(2)Ma 等与Mason 等提出的归一化经验模型适用性较强。对于致密储层,表面活性物质介入后重力对渗吸的影响十分关键。
(3)利用NB值可定性评价渗吸主要动力,修正后的NB值考虑了润湿性的影响。对于低界面张力环境,大部分是将重力与毛管力无因次时间标度融合归一化处理。
(4)带压渗吸可准确模拟实际油藏渗吸过程。修正的带压无因次时间模型消除了数据的分散性。利用此模式可预测和优化焖井时间,提高自发渗吸效率。
(5)时间标度归一化模型可推广至采收率归一化模型,从而更精确描述复杂多孔介质的渗吸过程,对评估和预测真实油藏原油采收率具有指导意义。
符号说明




