一种康复训练机器人的机构位置逆解
周 烨
(常州刘国钧高等职业技术学校,江苏 常州 213000)
据统计,我国有超过1 000万脑卒中患者,这些患者中幸存下来的大约有75%的患者留下诸多后遗症,如偏瘫、肢体无法正常运动等,其后遗症严重的则会导致生活不能自理[1]。在对后遗症进行治疗和护理的过程中,需对患者进行康复训练。患者的康复训练大多依赖基础医疗器械,随着机器人在康复医学中的应用且效果显著,其应用越来越广泛,且种类也越来越多[2-3]。
在对康复机器人机构进行设计时,通常有2种方式:一种是已知患者的身体条件并将其转化为机器人机构的输入进行正向求解,得出机构的康复训练执行结果,这种方式也称为机构的正解;另一种是将患者期望的康复训练结果作为输入,对机构进行反向求解,获得机构的输入函数,这种也称为机构的逆解。本文对某一康复机器人机构展开研究,对其机构进行逆解计算。
1 肩关节构型选择
人体上肢关节分为肩关节、肘关节和腕关节。肩关节是人体上肢关节中最为重要的球窝关节,本文选择对肩关节康复训练展开研究。牵引式康复训练机器人机构可通过牵引人体上肢末端(手部)进行康复运动,完成人体肩关节的运动,从而实现人体上肢肩关节的康复训练。在机构设计上并联机构在运动学上具有诸多优点:在运动过程中惯性低、刚度大且负载能力强等,因此成为康复训练机器人机构设计的首选。并联机构由静、动平台以及运动支链组成,综合考虑人体肩关节的运动性能,同时根据前人的分析可知,3-RRS(为球面并联机构的简称)可实现动平台上下运动,故将3-RRS球面并联机构作为实现肩关节构型。
当前学者在机构逆解的算法方面做过较多研究,肖帆在其毕业论文中对复杂多关节工业机器人逆解算法进行了分析和综述,并对唯一域求逆运动学的方法进行了研究和计算[4];同济大学的曾氢菲等对一种多臂协同焊接机器人的运动学进行了逆解,采用的计算方法是基于BP和RBF神经网络方法,其计算结果表明该方法计算精度较高[5]。本文在综合前人的研究基础上结合其研究对象的机构特点,采用矩阵法和闭环矢量法相结合的方法对其进行分析计算,以期获得机构的逆解。
2 3-RRS肩关节康复训练机器人机构的运动分析
需进行康复训练的患者,按日常生活常识当手臂水平位置或者低于水平位置时会由于手臂自身重力而自动下垂,此状态的机构康复训练研究不具有实际意义。因此本文以上肢处于水平位置为零度基本位置,以前屈角度为正向角度展开研究,此状态下上肢手臂的研究最大角度范围为0°~90°。
将人体上肢简化为3-RRS机构中的杆件,同时将3-RRS倾斜一定角度就能够实现肩关节的康复训练,这也是采用3-RRS机构分析的优点[6-8]。将上肢手臂总长用e表示,并假设康复训练的患者手臂运动为直线运动,则其掌心(机构终点)的运动轨迹为一弧形,为此掌心的运动起始点、运动终点、肩关节(机构起点)这三者的连线构成一个等腰三角形(见图1),其中,e为上肢总长。

图1 肩关节运动曲线

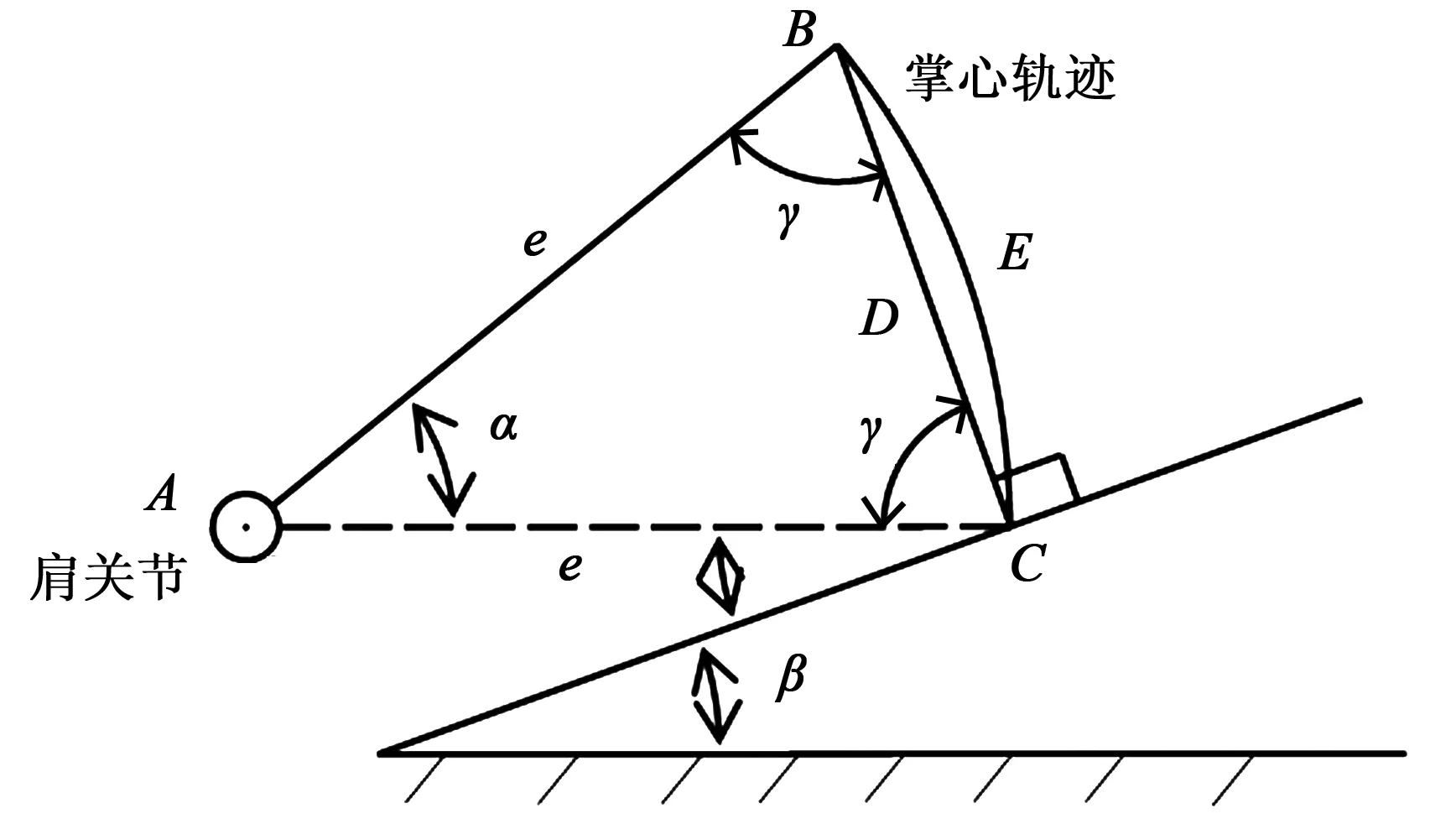
图2 肩关节运动简图
(1)
进一步构建3-RRS机构的运动示意图如图3所示,用a表示机构的3条支链中的下支链长度,用b表示机构的3条支链中的上支链长度。则在图3中,根据机构的几何关系,不难看出存在这样的关系:角度ψ的取值范围为0°~180°,即0°≤ψ≤180°。这样就可以得出杆件l的取值范围:当ψ=180°时,lmax=a+b;当ψ=0°时,lmin=|a-b|。
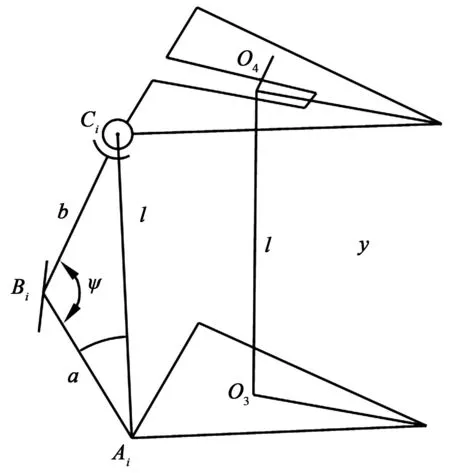
图3 3-RRS机构运动示意图

3 康复机器人肩关节机构的位置逆解
将整个求解过程转化到上述机构中,则并联机构位置逆解指的是:已知并联机构运动平台的位置参数,求解与静平台连接的输入部件的基本条件。本文采用矩阵法和闭环矢量法相结合的方法对3-RRS机构进行位置逆解。
设3-RRS两个平台的几何中心到各端点的距离分别为lO4Ci=r,lO3Ai=R(i=1,2,3)。那么在系统坐标系OXYZ下完成3-RRS并联机构位置逆解的分析,可根据预知的康复训练结果反过来求解3个支链的具体输入函数[9-10]。
设底座固定坐标系为O2X2Y2Z2,静平台坐标系为O3X3Y3Z3,根据3-RRS机构的应用条件,静平台坐标系O3X3Y3Z3绕底座固定坐标系O2X2Y2Z2中X轴旋转θ角,则坐标变化矩阵T1可表示为:
(2)
矩阵T1表示由底座固定坐标系O2X2Y2Z2向静平台坐标系O3X3Y3Z3转换的坐标变化矩阵。在静平台坐标系O3X3Y3Z3中,Ai(i=1,2,3)点的坐标为:

(3)
则Ai在固定坐标系O2X2Y2Z2中的坐标Ai(底)可用下式求解:
Ai(底)=T1·Ai
(4)
以经典的ZYZ型欧拉角(α,β,γ)表示动平台姿态,c表示cos,s表示sin(下同)。

(5)
用ci、Ci和CO2i分别表示动平台上球副中心点Ci(i=1,2,3)在局部动坐标系O4X4Y4Z4、静平台坐标系O3X3Y3Z3和固定底座坐标系O2X2Y2Z2中的位置矢量。CO4、CO3和CO2分别表示动平台球副中心点Ci(i=1,2,3)在局部动坐标系O4X4Y4Z4、静平台坐标系O3X3Y3Z3和底座固定坐标系O2X2Y2Z2中的齐次坐标矩阵。则有:CO3=T2·CO4,CO2=T1·T2·CO4。
在动平台坐标系O4X4Y4Z4下,ci点坐标为:

(6)
将式6带入CO2=T1·T2·CO4中可得:
(7)
因为铰链中心Ai、Bi均为转动副,所以Ci只能和Ai、Bi在同一个平面内移动,由此列出约束方程如下:
(8)
联立式7和式8,消除中间变量CiO4(i=1,2,3)的坐标参量,可获得OO4O3的坐标参量关系方程式:
(9)
为求解动平台中心O4在底座固定坐标系O2X2Y2Z2中的位置参数,由静坐标系与底座固定坐标系的变换矩阵T1和O4在静坐标系O3X3Y3Z3中的位置坐标(XO4O3,YO4O3,ZO4O3),可得O4在底座固定坐标系O2X2Y2Z2中的位姿参数。
OO4O2i和OO4O3i分别为动平台中心O4在底座固定坐标系O2X2Y2Z2和静坐标系O3X3Y3Z3的位置矢量,OO4O2和OO4O3分别为动平台中心O4在底座固定坐标系O2X2Y2Z2和静坐标系O3X3Y3Z3的坐标矩阵,则有:OO4O2=T1·OO4O3,同时计算可得:

(10)
(11)
由此推出动平台中心位置的位姿,且得出其位置坐标与静平台转动角度θ之间的关系。
由式5可知,该机构6个姿态参量选取其中任意3个(必须包含ZO4O3)即可确定该机构姿态,在此处取ZO4O3、α、γ为已知参量,则动平台姿态确定。
根据空间矢量关系,铰链AiCi长度矢量LAiCi可表示为:LO3Ci=LO3Ai+LAiCi,LAiCi=LAiO3+LO3O4-LCiO4。其中,LO3Ci表示O3到Ci的矢量,LO3Ai表示O3到Ai的矢量,LAiCi表示Ai到Ci的矢量,LO3O4表示O3到O4的矢量,LCiO4表示Ci到O4的矢量。
由此,该机构位置逆解即已知ZO4O3、α、γ这3个参量,求解各个支链与静平台夹角θi1,以及两支链间夹角ψ。
已知动平台中心的位置坐标和变换矩阵,易得动平台各个中心点的位置坐标。在三角形AiBiCi中,根据余弦定理,可建立两支链间夹角方程:
(12)
式中,θi1为构件AiBi与静平台的夹角;L1i为构件AiBi的长度;L2i为构件BiCi的长度;Li为构件AiCi的长度。求解式12,便可得θi的值。
上述求解便求得了康复训练机器人机构的杆长、夹角。
4 结语
本文对肩关节康复训练机器人机构在抽象简化后进行了运动分析,利用机构的几何关系和运动关系采用矩阵法和闭环矢量法相结合的方法详细推导了机构的位置逆解,获得了康复患者在期望的康复训练结果下机构3个支链的具体输入函数,即将期望的康复训练执行动作作为已知条件对机构进行了反向设计,求取了机构的杆长、夹角等参数,其求解结果及分析过程能够缩短机器人的设计开发周期,且通过计算可以准确地获得机器人机构杆件的长度,进而为机器人的生产制造提供很好的生产指导,结果具有一定的工程实际应用价值和参考意义。

