贯入器头锥外形优化设计

孟丽霞，王莽宽，刘士明，杨谢柳

（沈阳建筑大学机械工程学院，辽宁 沈阳 110168）

1 引言

为了解星体资源分布情况、星体土壤组成以及获取星体演化过程等科学研究，均需对星壤的物理特征进行研究，其关键是能将科学探测仪器送入浅层星壤的原位探测设备。原位探测设备中冲击式贯入器凭借结构简单、质量小、探测成本低、贯入深度不受限等优点成为研究的热点［1］。德国宇航局DLR研制的PLUTO 冲击式贯入器搭载在‘猎兔犬2 号’火星探测器上并于2003 年发射，PLUTO 贯入器虽然总长度只有280mm，直径在20mm 左右，却可以实现1.5m 的钻探深度，不过任务失败未能成功在火星上实际运用。之后DLR 根据PLUTO 又研制多款冲击式贯入器，例如HP3 贯入器被NASA 的洞察号搭载已经在2019年于火星上着陆［2］。

冲击式贯入器一般由驱动单元、冲击锤、壳体、驱动弹簧和缓冲弹簧五个部分组成，如图1所示。其中，各部分的参数选择决定贯入器是否能正常工作［3］。贯入器的壳体一般由圆柱形的柱体和一个头锥组成，贯入器头锥的外形形状有很多种，MMUM使用纺锤形的头锥，并且在头锥上集成了微型采样机构，可以通过此机构获取少量样本［4］，目前正在火星运行的HP3贯入器也采用的是纺锤形的头锥，但是无采样功能［5］；相较于上述规则形状的头锥，KRET采用非线性变化的锥形头部，其尖端呈45°锥形角，到后部过渡到30°锥形角［6］；文献［7］对内凹形的头锥展开了相关的研究。

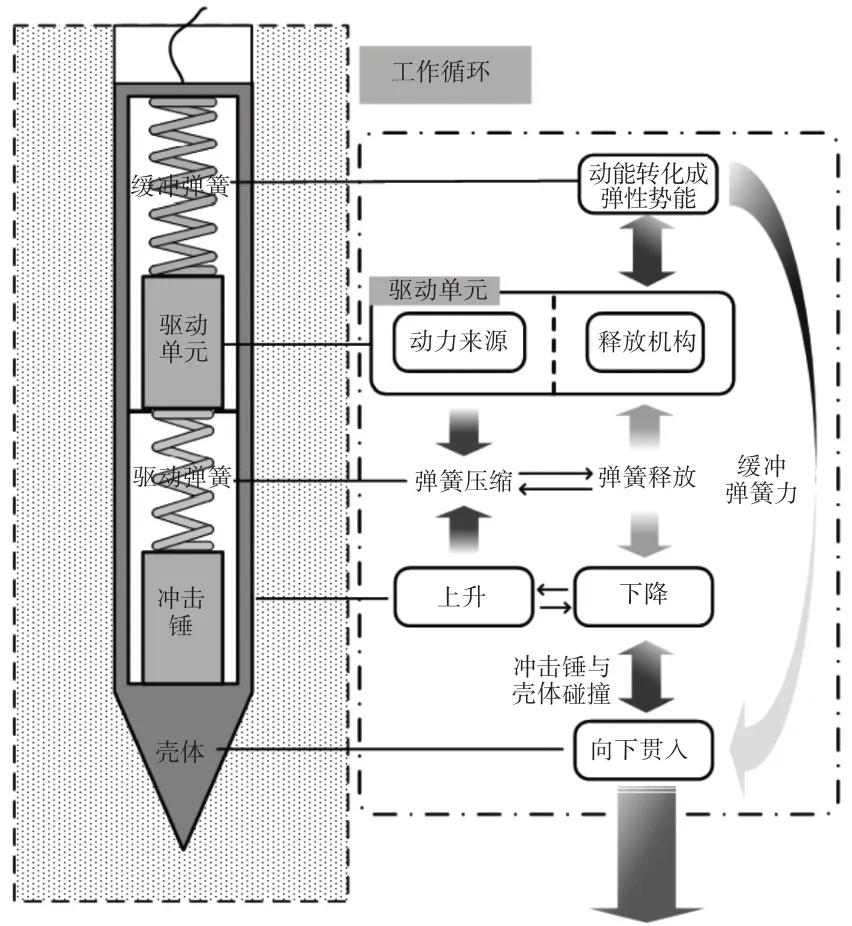
图1 贯入原理示意图Fig.1 Schematic Diagram of Penetration Principle

冲击式贯入器在贯入的过程中，头锥起到挤入穿透土壤的作用，其所受的阻力除了摩擦力以外还有反挤入力等，而外壳其他的部分不参与挤入过程，只受一定的滑动摩擦力，根据相关研究，壳体所受的阻力有90%集中于头锥部位［8］。因此，头锥的外形设计决定着贯入器所受阻力的大小，阻力越小单次冲击下的贯入距离越深，进而影响贯入器的整体贯入性能。现有文献主要对锥形、纺锤形、内凹形头锥进行了相关的研究，研究头锥曲线在各个位置的曲率变化和锥角改变对贯入所受阻力的影响［9］。但是否还存在其他形状且阻力更小的头锥，还未见相关的研究文献。

因此，这里提出利用三次样条插值建立以坐标为变量的任意形状头锥的曲线方程，在传统的土壤穿透模型的基础上［10］，建立任意曲线头锥所受阻力的微分方程。采用遗传算法获得具有最小受力的头锥曲线，并借助离散元软件进行仿真，验证优化结果。

2 贯入器工作原理与头锥建模

2.1 工作原理

贯入器整体为一个圆柱体，驱动单元为整机的动力来源，其内部的驱动机构提升冲击锤进而压缩驱动弹簧，如图1所示。在提升到一定高度后，驱动单元的释放机构将冲击锤释放，并在弹性势能的作用下与壳体发生碰撞。与此同时，驱动弹簧的反向作用也会促使驱动单元产生反贯入方向的运动，进而压缩缓冲弹簧，驱动弹簧的反向作用转化为驱动单元的动能和缓冲弹簧的势能，若参数设置得当，则贯入器所受到的正向作用力始终大于反向作用力，促使贯入器向下贯入。单次冲击作用距离比较小，因此贯入器的工作过程是一个周期反复冲击的过程。由图1可以看出，贯入器内部的作用力最终完全作用在壳体上，与外界环境进行交互作用的也只有壳体，壳体的尖状头锥将土壤向两侧挤压，从而使贯入器向下贯入，若在内部参数不变的情况下提高贯入器的贯入深度与贯入效率，头锥外形的设计极为重要。

2.2 头锥外形建模

根据前文所述，贯入器的头锥需要在贯入过程中起到一个挤入的作用，根据土力学的相关知识，为保证足够的穿入力，不论任何一种形状，最终都会在末端形成尖端以增大穿入压强。合理的锥形设计，可以极大地提高贯入效率。常见的几种形状的头锥，其中贯入器的直径2R和长度L为头锥的基本尺寸，如图2所示。直径2R大小要充分考虑内部元件的安装和保证足够的强度，因此，2R的大小取决于内部设计，是在头锥进行设计之前就已经确定完毕的，在头锥的设计与优化过程中可以认为是一个定值。L为头锥的长度，与贯入器内部元件的设计无关，其大小也决定着头锥的外部形状，是优化设计的变量之一。由图2可知几种不同形状的头锥，其中纺锤形和内凹形都可以分为定曲率和变曲率两种，其曲率也是影响因素之一。为了进行通用性研究，这里提出了图2中的任意形头锥，任意形的意思是可以代表任意的连续光滑外形曲线。

图2 几种不同形状的头锥Fig.2 Different Shapes of Head Cone

贯入器头锥可以认为是一条曲线绕其中心轴旋转而成的几何体，要研究头锥所受的阻力，可先研究这一条曲线所受的阻力，之后利用积分的方式获取整个头锥所受到的阻力大小。因此，首先需要建立任意形状头锥的曲线。建立的坐标系，为方便描述将曲线置于坐标系的第一象限，以保证点的坐标值均为正值，如图3所示。使用任意n个形值点将曲线分割，点与点之间通过三次样条曲线进行连接。n的大小可以根据情况适当增加或减少，增加可以提高曲线拟合的精确度，过多则会引起计算复杂。

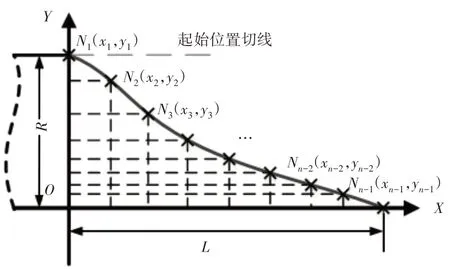
图3 任意形状头锥的曲线表述Fig.3 Curve Representation of Arbitrary Shape Head Cone

采用三次样条插值对任意n个形值点进行拟合，形成一条以形值点坐标为变量的分段三次样条曲线，任意一段三次样条曲线的描述如下：

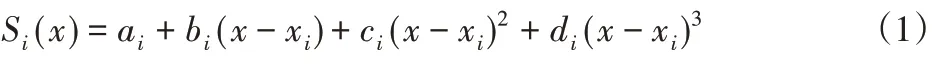
其中，i=1，2，3…n-1，要求xi＜xi+1，步长hi=xi+1-xi，符号ai，bi，ci，di的表达式为：

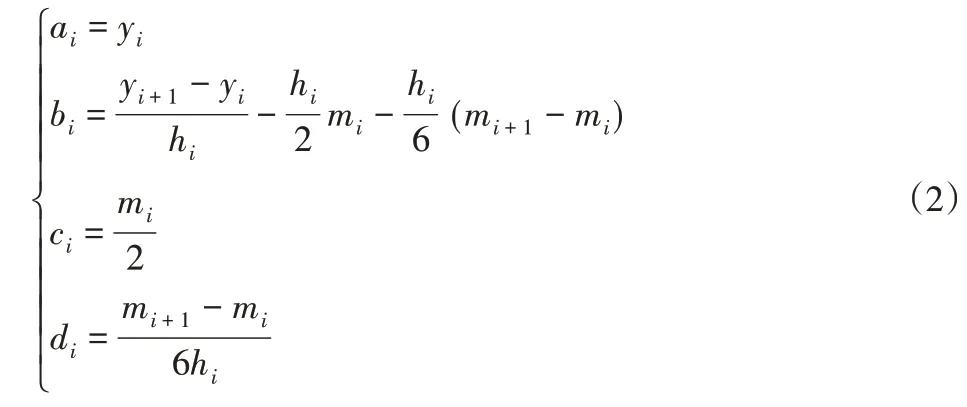
图3中曲线从y轴起始，在起始点处，为了保证曲线光滑，起始点处的曲线需要与外壳相切，则起始点处的斜率需要被指定为一个定值。

末端点的斜率无特殊要求，因此为自由斜率，则：

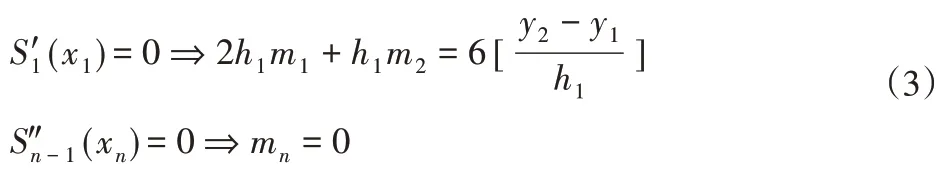
为了保证曲线的光滑性以及连续性，需要保证：

根据式（4）的条件，对mi进行求解，求解矩阵如下。

对式（5）进行求解，将所得mi值带入式（1）中，即可求得各段曲线的方程。

3 曲线与土壤作用建模

冲击式贯入器利用内部产生的冲击，使得贯入器对土壤产生挤压作用超过土层的剪切强度后，贯入器的尖端头锥将土壤向两侧挤压，使两侧土体产生破坏。文献［11］根据土壤动力学提出贯入器头锥与土壤穿入过程中的力学模型。其假设土层为一个半无限的土体，将土壤的极限平衡区分为三个区域，Ⅰ区称为弹性压密区，Ⅰ区的土壤与贯入器的头锥产生直接接触，贯入器向下移动的过程中，将此区域的土壤向两侧挤入；Ⅱ区称为过渡区，Ⅲ区为朗肯被动区，贯入器向下贯入的过程中，将力通过Ⅰ、Ⅱ区传递给Ⅲ区达到失效状态。在不断的贯入冲击作用下，土壤颗粒由两侧向下移动，从而使贯入器向下贯入。

以任意形状的头锥为例，绘制星壤极限平衡区的分析示意图，如图4所示。图中假设土壤为无限土体，H'为贯入器头锥末端到地面的距离，H为贯入器头锥尖端贯入的距离。

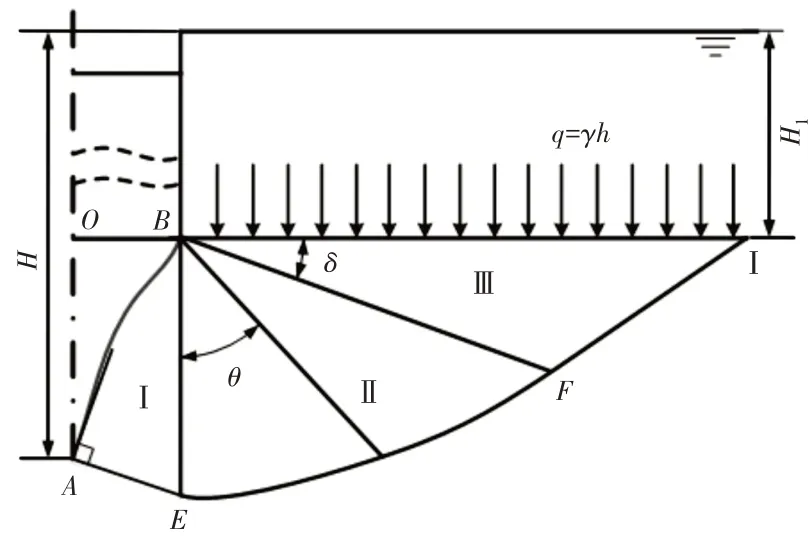
图4 星壤极限平衡区分析Fig.4 Analysis of Equilibrium Limit Region of Soil

为了求得由样条曲线组成的任意构型头锥所受的阻力，需要对图4中所述的土壤体进行力学分析，如图5所示。

图5 Ⅱ，Ⅲ区土壤平衡受力Fig.5 Ⅱ，ⅢArea Soil Balance Force

在滑裂的月壤区Ⅱ、Ⅲ内取月壤体BEFK进行受力分析，文献［11］根据其力学平衡原理，求得在BE面上的法向应力，其中推导过程见文献所述，这里不再赘述，直接给出BE面上的应力大小：

式中：Nq、Nc—月壤颗粒的承载力系数，与月壤的内摩擦角有关。

根据式（6）可以求得Ⅰ区BE面上所受到的正压力，取出I区的土壤体剖面ABE并对其进行受力分析，如图6 所示。土壤体ABE的BE面受Ⅱ区土壤的正压力PF'与相对滑动作用产生的剪切力，AE面受力作用与BE面相似，AB面与贯入器的头锥直接接触。贯入器头锥受到其它面传递给AB面的正压力PA'，任意点的正压力的方向垂直于该点处的切线，同时正压力也会对贯入器头锥产生摩擦力fA'，任意点上的摩擦力的方向与该点的切线运动速度方向相反。根据力的相互性，土壤体ABE上也会产生与贯入器头锥受力大小相同的反作用力，由上述假设可知，土壤体ABE属于临界平衡状态，求得PA'即可求得贯入器头锥所受的阻力。求AB面上所受的应力在x轴的分量Qx与在y轴的分量Qy，采用微分的方式建立其作用方程，之后利用积分直接求得AB面上的应力大小，微元区域受力，如图7所示。

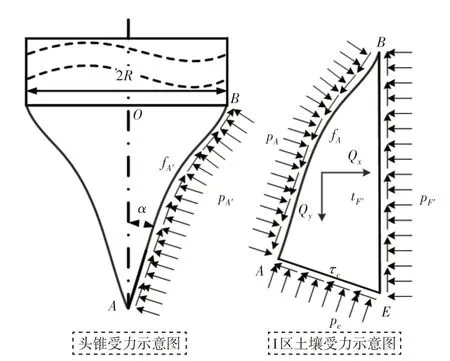
图6 头锥总体受力分析图Fig.6 Overall Force Analysis Diagram of Head Cone

图7 头锥微分区域受力分析图Fig.7 Head Cone Differential Zone Force Analysis Diagram

将所受到的正压力与摩擦力进行分解，则每个微元曲线上的应力大小为：

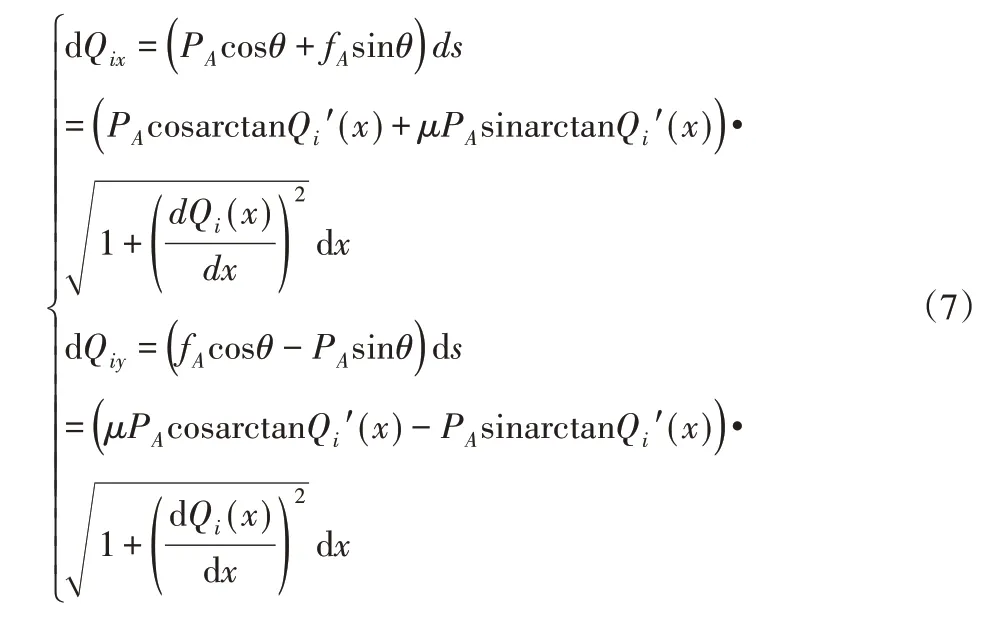
其中，i=1，2，3…，n-1，则每段曲线上所受的应力为：

对每段曲线上的值进行累加可得x方向与y方向的所有应力值的大小为：

依据力的平衡条件，列出土壤体的平衡方程为：

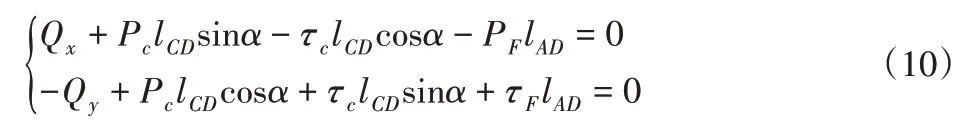
根据库伦公式，上式中所有的剪切力的计算公式均为：

将上述各个等式联立，即可求得贯入器头锥所受的应力大小PA的值，前述分析过程均建立在一个剖面上，对一条线上所受的应力大小进行分析，为了求得贯入器总的阻力大小，需要对曲面进行分段积分。钻头总体受力，如图8所示。首先需要求微元的面积为：

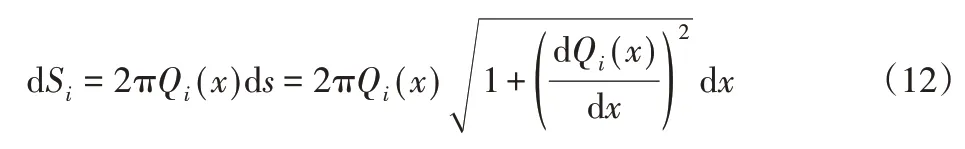
由于贯入器头锥是由一个曲面沿着轴线旋转所得，在假设土壤为均匀土壤的条件下，土壤微元面上所受的沿着y轴方向的作用力均指向轴线，如图8中头锥的某一切面所示，因此y轴所受到的力抵消，所以最终贯入器头锥所受的贯入阻力方向沿x轴，与贯入器运动方向相反。任意形状下的贯入器头锥是由多段光滑曲线光滑连接而成，任意一段曲线微元所受的阻力为：

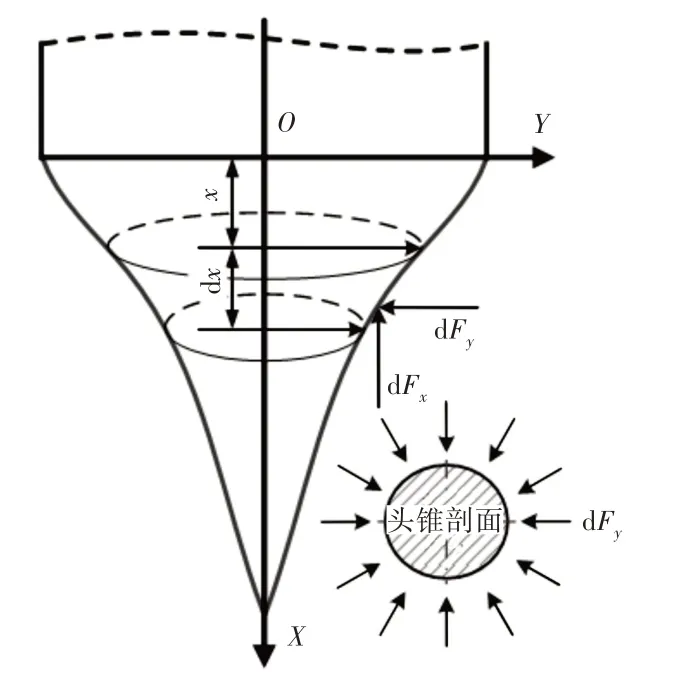
图8 钻头总体受力图Fig.8 Total Force on Bit

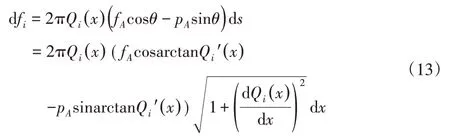
将每段曲线所受的阻力进行累加，则整段曲线所受到的阻力以及贯入器头锥所受到的阻力为：

根据式（14）即可获得任意形状头锥与土壤作用阻力大小的方程，方程中含有的未知量为曲线的坐标。

4 贯入器头锥形状的最优化求解与仿真验证

为了获得贯入器头锥所受阻力最小的曲线，以上述所得的方程为目标，通过适合的优化算法获得使阻力最小的坐标点，最终通过坐标点得到贯入器头锥外形的最优解。由于点的数目较多，搜寻的范围大，方程复杂，传统的寻优算法过多的依赖目标函数本身的性质如斜率等，组成头锥形状的曲线是分段式方程描述，无法求解方程整体的斜率，因此传统的算法不适用。遗传算法主要依赖目标函数的值作为适应度函数，不依赖函数自身的属性。这里将头锥的阻力方程封装为一个函数，以点的坐标为变量，使用遗传算法搜寻使头锥受力最小的一组坐标解，遗传算法的框图，如图9所示。

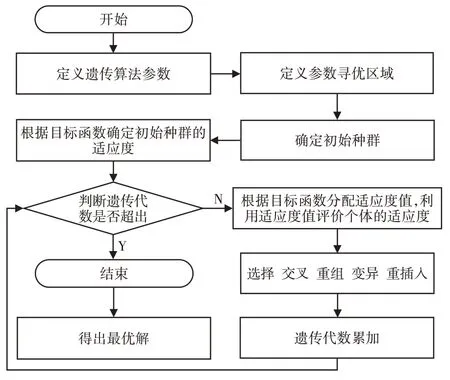
图9 遗传算法框图Fig.9 Block Diagram of Genetic Algorithm

所受的阻力方程（14）含有一定的未知数，难以求解具体的解析解，根据遗传算法的特征，优化过程中每一种群的个体都是一个确定的数值集，可以利用Matlab直接求解阻力方程的数值解进行比较。如图3所示，为了进行一般性的探究，将坐标点数据进行归一化，横坐标为L/R，纵坐标范围为（0～1），为简化变量的数目，每个点之间的间距相同，点的数目多少决定生成曲线的准确度，由于贯入器的头锥尺寸不大，在保证精度的前提下尽量减少计算量，最终选择组成样条曲线的点数目共有11个，搜寻的变量为各个点的y轴坐标与L的大小。

遗传算法的参数设置会对遗传算法的搜寻结果造成较大的影响，遗传算法基本参数设置，如表1所示。设置完毕以后搜寻所得的点坐标，如表2所示。

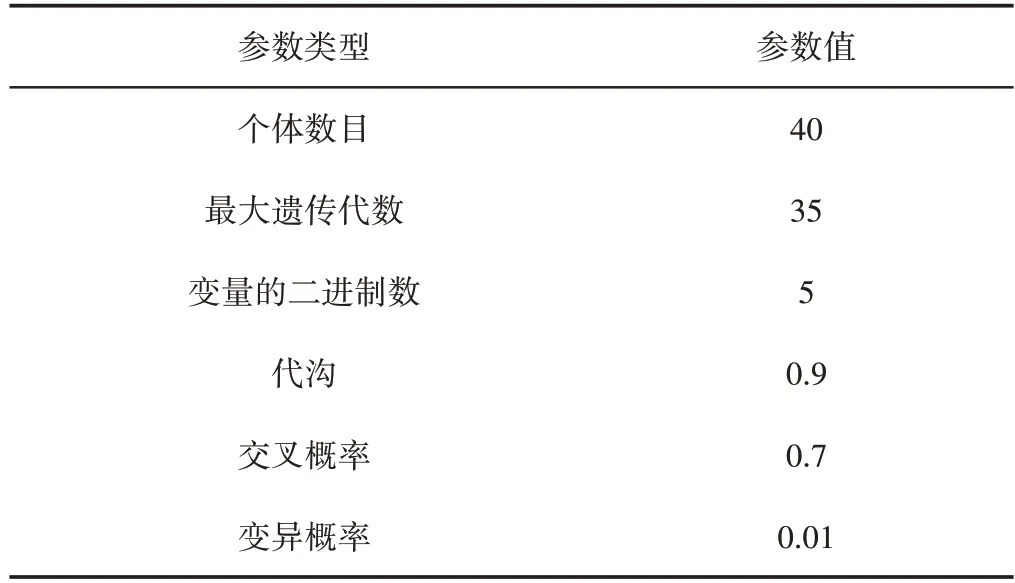
表1 遗传算法的参数设置Tab.1 Parameter Setting of Genetic Algorithm

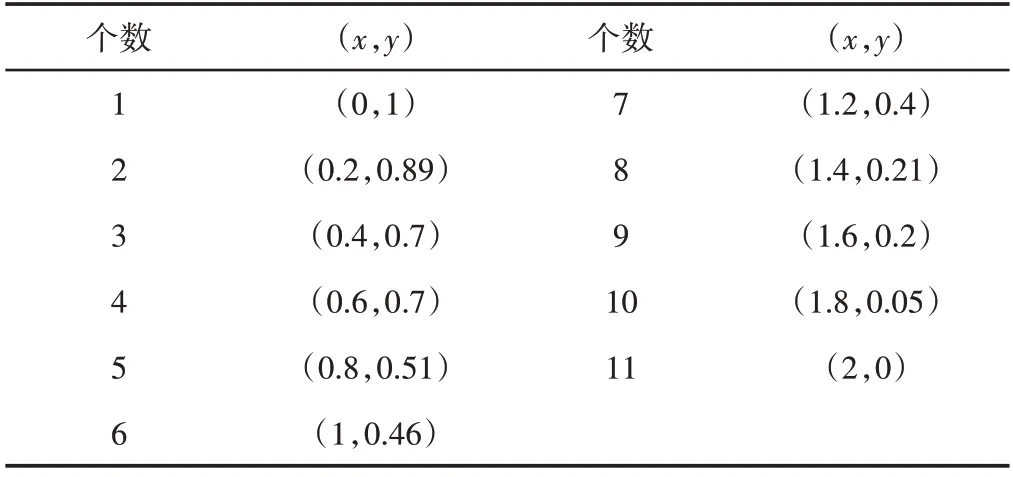
表2 优化所得坐标点Tab.2 Optimize the Resulting Coordinate Points

根据表2所得的数据，绘制受力最小的头锥，如图10所示。为了验证所得结果的正确性，根据上述所得的最优化构型绘制钻头的三维图带入离散元软件，与图2中基本尺寸相同的纺锤形、内凹形、锥形构型进行仿真对比。离散元仿真的示意图，如图11所示。贯入器三维模型以一定的速度插入模拟土壤颗粒中，利用离散元软件的后处理功能求解在匀速运动过程中随时间变化的平均阻力。

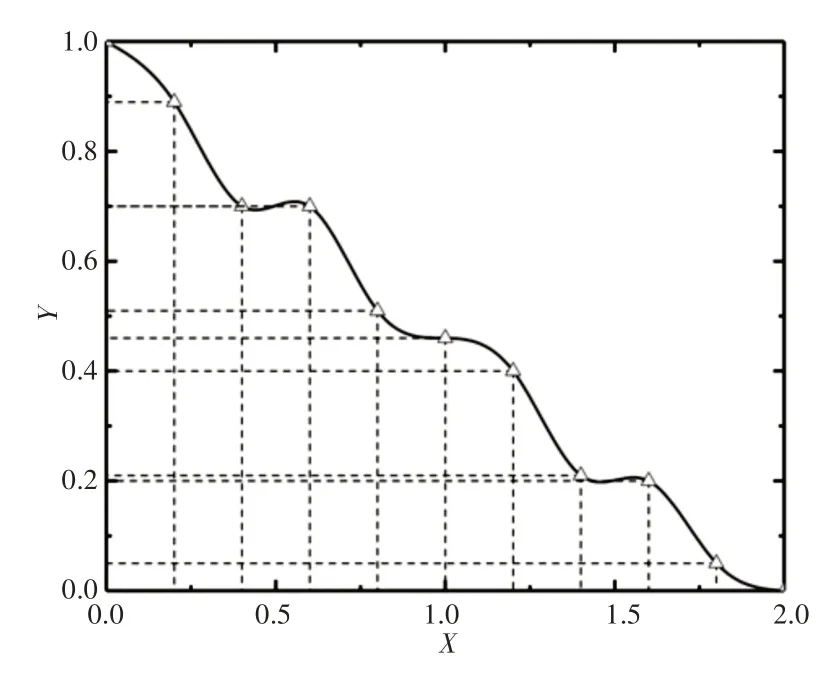
图10 优化后所得的头锥外形Fig.10 Optimized Head Cone Profile

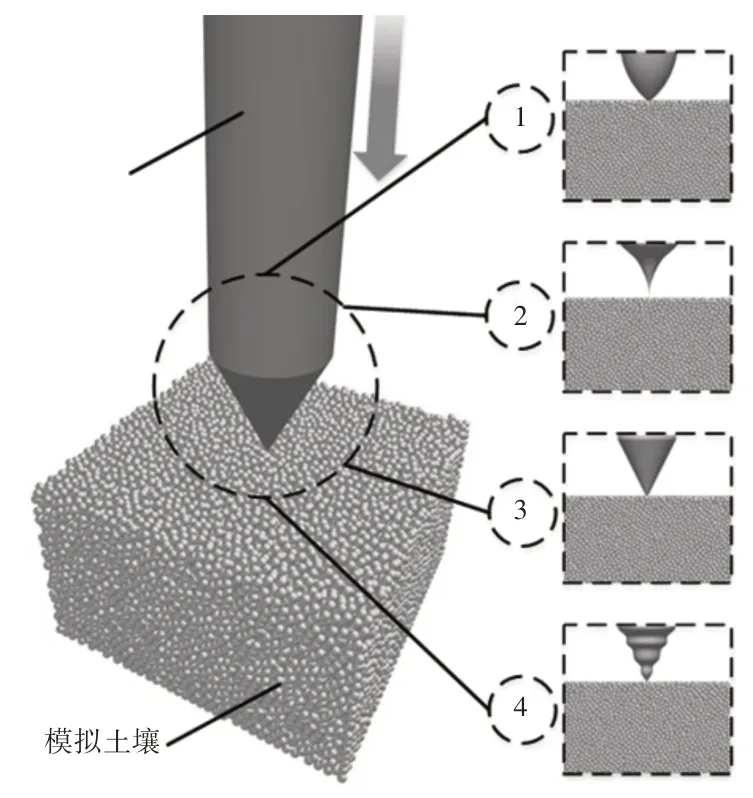
图11 离散元仿真图Fig.11 Discrete Element Simulation Diagram

由于上文中仅对贯入器头锥所受的阻力进行分析，因此仿真在头锥完全浸没为止即停止仿真，所得的仿真曲线对比，如图12所示。图中所得最优构型在钻头浸入土壤的过程中相对于其他形状来说所受到的平均阻力较小，因此求得最优构型结果正确。

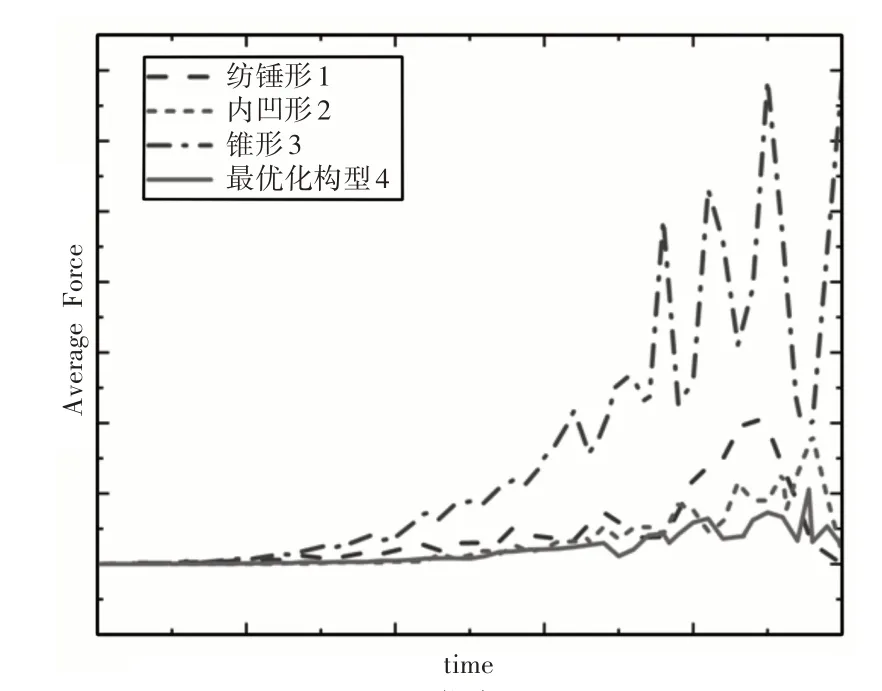
图12 仿真对比Fig.12 The Simulation Comparison

5 结论

（1）在对头锥的研究中提出任意形状的头锥曲线，利用三次样条插值以各点的坐标值为变量，建立起任意形状头锥的曲线方程。（2）根据所得曲线方程，结合相关文献与土壤力学，得到任意形状的头锥与土壤作用的微分方程。（3）确定影响贯入器头锥形状的坐标变量以及变量的个数，将头锥与土壤的作用方程带入遗传算法，以获得最小的阻力值为遗传算法的优化目标，获得最优解。（4）利用所得坐标的最优解建立贯入器头锥的三维模型，带入离散元软件，与其他基本尺寸相同的头锥进行仿真对比以验证最优解的正确性。这里提出的具有不同于传统形状的头锥拥有较小的潜入阻力，因此理论分析和仿真分析能为以后冲击式贯入器头锥的研制提供理论依据和支撑，可以在不更改内部参数的情况下提高贯入器的穿入能力。