面向离散型半自动化混流包装线的生产任务管控研究

俞云强，张 豪

（无锡职业技术学院，江苏 无锡 214125）

1 引言

随着制造业逐步迈入工业4.0时代，客户对产品的需求特征正在由“满足基本功能需求”过渡到“实现差异化需求”，而生产模式也逐渐从大批量生产向多品种/小批量发展，甚至在特定行业的特定环节产生了以个性化需求的满足为特征的定制化生产模式［1-5］。现代包装生产体系也随之进行了相应的升级，介于手工包装线和全自动化包装线之间半自动化包装线，即自动化设备与人工作业并存，具有典型的离散化特征。由于离散型半自动化包装线便于柔性化管理，国内包装行业大多采用该模式。对包装线进行合理改造以实现混流生产，既节约成本，又能满足客户的差异化需求［6-8］。在此背景下，如何实现离散型半自动化混流包装线生产任务的科学管控，满足包装行业的准时化（Just In Time，JIT）生产需求，进而提升包装行业生产控制的智能化水平，已经成为当前包装业界亟待解决的关键性问题。

离散型半自动化混流包装线的生产体系具有周期长、节点多、工艺复杂等特点，混流生产模式更加剧了生产过程中设备故障、人员调整等不可控因素的影响。在离散型半自动化混流包装线上，生产任务由订单计划分解而来，包含多个工序，并按工序顺序在包装线的工位上依次执行。每个生产任务均具有不同的特征，这些特征导致它们的优先级各不相同。由于生产计划下达的超前性，会出现生产任务的积压，从而导致传统调度理论和方法的应用效果很差，无法为JIT目标的实现提供支持。因此，这里建立了离散型半自动化包装线生产任务管控的两级框架，其中第一层针对包装线级，提出包装线工艺任务的优先级评定方法；第二层针对工站级，提出工序任务的序列迭代优化方法。然后，结合卧式钢卷包装生产线，对所建立的离散型半自动化包装线生产任务管控框架的具体应用实施过程进行讨论。

2 离散型半自动化混流包装线生产任务管控的两级框架

对于包装企业而言，在准时化生产的目标下，包装线级和工站级的生产任务管控目标具有明显的差异。针对包装线级，对应人群为企业管理人员，对应工作规范为该产品的整体包装工艺，对应任务为在包装线上执行的整体工艺任务，管控要点为确定任务的优先级、为任务下达提供决策支持；针对工站级，对应人群为作业班组，对应工作规范为在该工站执行的单个工序，对应任务为在该工序任务，管控要点为任务序列的优化。因此，面向离散型半自动化混流包装线，分别针对包装线级和工站级的生产任务管控目标，建立离散型半自动化混流包装线生产任务管控的两级框架，如图1所示。

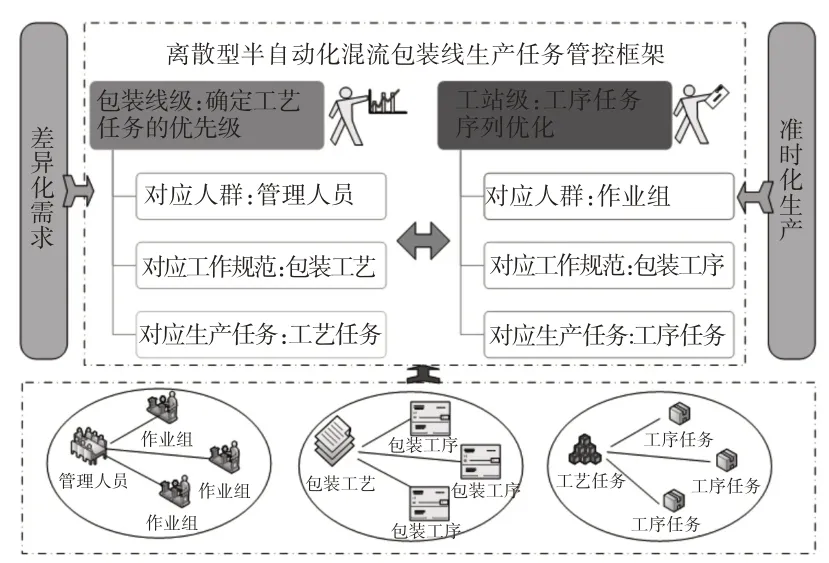
图1 离散型半自动化混流包装线生产任务管控框架Fig.1 Production Task Management and Control Framework of Discrete Semi-Automatic Mix-Flow Packaging Line

以某大型钢铁制造企业的卧式钢卷半自动化包装线为例，该包装线是由多个工站组成的柔性生产线，能够执行多种型号卧式钢卷的包装生产任务。在包装线级，对应生产任务为某型号卧式钢卷的整体工艺任务；对应工作规范为该型号卧式钢卷的包装工艺，由多个工序组成，如钢卷上料、放置内芯防锈纸、包外周防锈纸、套塑料套、包纸护角、包周免平板纸等；对应人群为管理人员（一般为车间主任、生产计划下达部门等）。管理人员首先根据订单，明确将要下达的多个包装生产任务，然后确定这些任务的优先级，将多个包装生产任务下达给相应的包装线，为生产控制提供决策依据。而在工站级，对应生产任务为该工站当前将要执行的所有工序任务，如打捆工站目前有3个待执行的工序任务：（1）A型号卧式钢卷的周向打捆工序任务；（2）B型号卧式钢卷的径向打捆工序任务；（3）C型号卧式钢卷的周向打捆工序任务；对应工作规范为相应的包装工序；对应人群为该工站对应的作业班组。因此，工站级的生产任务管控要点是对作业班组的待执行工序任务序列进行优化。

3 包装线任务的优先级评定

3.1 包装线任务优先级评定模型

通过对包装企业和现有文献的调研［6-10］，归纳出影响包装线任务优先级评定的众多属性并将其进行层次化处理，构建离散型半自动化包装线的任务优先级评定层次化模型（Hierarchical Model for Task Priority Evaluation，HMTPE），如图2所示。

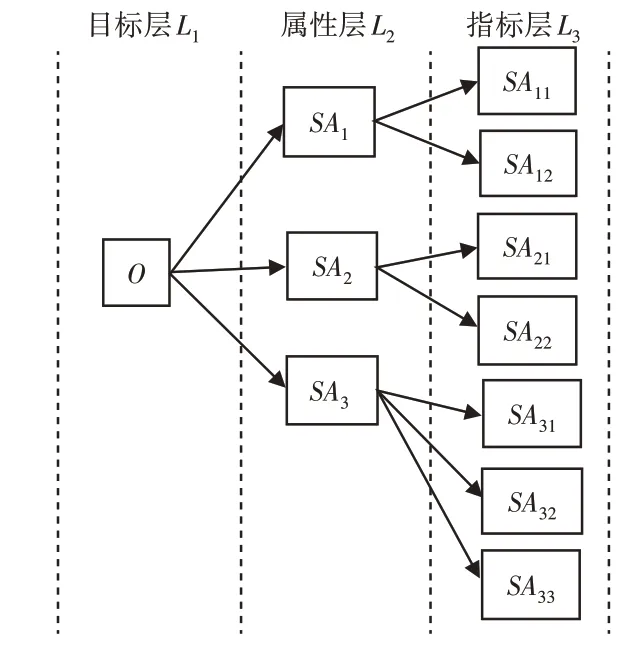
图2 包装线任务优先级评定层次化模型Fig.2 Hierarchical Model for Task Priority Evaluation in Packaging Line

HMTPE包含三层：目标层L1、属性层L2、指标层L3，如图2所示。目标O由包装线任务的紧急性SA1、生产类型SA2和包装线承载能力SA3等三个属性决定。相关定义如下：

定义1：紧急性SA1。SA1包括订单紧急性和额外紧急性，分别用指标SA11和指标SA12表示。从高到低将紧急性分为特急、紧急、较急和普通四个级别，对应四级评语｛高，较高，较低，低｝，取其等级值为｛0.8，0.6，0.4，0.2｝。

（1）SA11指的是包装线任务的订单紧急性，从ERP 系统中获取；

（2）SA12则是包装企业接受订单后，附加给包装线任务的紧急性。

定义2：生产类型SA2。SA2包括一级生产类型和二级生产类型，分别用指标SA21和指标SA22表示。

（1）SA21包括大量、成批、小批量，依次用PT1、PT2、PT3表示；

（2）SA22指的是包装线任务对应产品的用户，如建筑公司甲、石油公司乙、铁路公司丙等，设用户集为Cus=｛Cus1，Cus2，…｝。

采用专家评价法对SA21和SA22进行评价。假设专家人数为e名，评估等级为n级，对应评语为Opin=｛Opin1，Opin2，…，Opinn｝，对应数值为Ass=｛1/（n+1），2/（n+1），…，n/（n+1）｝。设一级生产类型的集合为PT=｛PT1，PT2，PT3｝，专家对PTi（PTi∈PT）的评语形成的集合为PT_Opin=｛PT_Opin1，PT_Opin2，…，PT_Opine｝（PT_Opinj∈Opin，1≤j≤e），则PTi对模糊评语Opink∈Opin（1≤k≤n）的隶属度为e，eik为专家评语集合PT_Opin中评语Opink的频数，那么PTi的评估值为；对于SA22采取同样的评价方法。

定义3：包装线承载能力SA3。SA3包括承载极值指标SA31、承载裕值指标SA32和承载率指标SA33。承载极值指包装线能同时承担任务的最大值；承载裕值指包装线承载极值与正在执行的任务数之间的差额。承载率指任务对应的包装线当前正在执行的任务数所占承载极值的比率，若承载率越高，则该包装线越繁忙，接受新任务投产的能力越差。

设生产计划中的包装线任务由W条包装线来执行，第i（1≤i≤W）条包装线的承载极值和当前承载分别为LNi和r_LNi（0≤r_LNi＜LNi），对于将由第i条包装线执行的任务，则SA31、SA32和SA33的指标值可分别表示为：LNi/max｛LNi｝、（LNi-r_LNi）/max｛LNir_LNi｝、（LNi-r_LNi）/LNi。

3.2 基于ANP的包装线任务优先级评定指标权重求解

包装线任务优先级评定是一个复杂的决策问题，如图2 所示。属性之间、指标之间均存在关联性。在求解指标权重时，传统层次分析法（AHP）［9，11］的核心思想是将指标体系划分为独立的层次结构，只考虑上层要素对下层要素的支配作用，且同层要素相互独立。然而，指标之间存在关联性和依赖性，如紧急性SA1受生产类型SA2、承载能力SA3的影响，需要在评定中给予反馈。因此，AHP不适用于求解包装线任务优先级评定的指标权重。网络层次分析法（ANP）［12-13］将系统元素分为控制层和网络层两部分，网络层的内部结构是交互影响的，能够解决上述问题，因此这里采用ANP来求解包装线任务优先级评定的指标权重。

首先建立包装线任务优先级的ANP网络结构。控制层包含目标O；网络层包含三个元素组，分别为：紧急性SA1、生产类型SA2和承载能力SA3，其中，SA1受其余两个元素组的影响，同时SA1自身包含的元素相互影响；SA3受SA2的影响，同时SA3自身包含的元素相互影响，如图3所示。

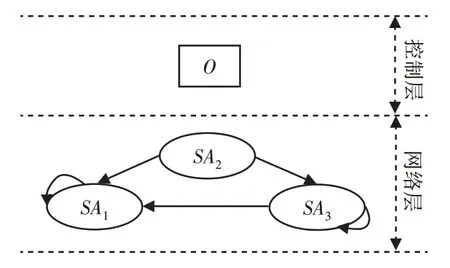
图3 包装线任务优先级的ANP网络结构Fig.3 ANP Network Structure of Task Priority in Packaging Line

为便于数学表达，控制层仅包含目标O，设网络层包含元素组SA1，…，SAN，其中SAi中有元素SAi，1，…，SAi，ni（i=1，…，N）。以目标O为准则，以SAj中元素SAj，l（l=1，…，nj）为子准则，基于SAi中元素对SAj，l的影响力大小，采用专家评价法进行SAi中元素的间接优势比较。设专家给出的评判矩阵为：

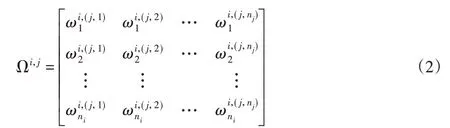
式中：列向量ωi，(j，l)—元素组SAi中元素SAi，1，…，对元素组SAj中元素SAj，l的规范化影响度评分向量。如果元素组SAj中元素不受元素组SAi中元素的影响，则Ωi，j=0。于是，得到控制层元素O下的超矩阵Ω：

此时，矩阵Ω中的子块Ωi，j已进行列标准化，但Ω尚未列标准化。为解决此问题，根据控制层元素O下SA1，SA2，...，SAN对SAj(j=1，2，...，N)的影响，执行间接优势比较，同理得到元素组SA1，SA2，...，SAN的相对重要度矩阵Ψ=(ψi，j)N×N：

3.3 包装线任务优先级计算

根据2.1中确定的指标值和2.2中求解得到的指标权重，设包装线任务集合为{T1，…，TM}，则对于Tk（k=1，…，M），其优先级Pk为：

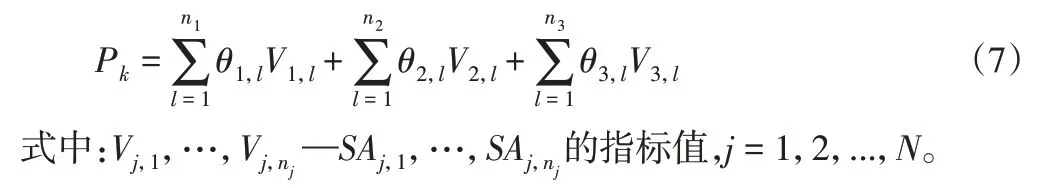
获得包装线任务的优先级后，可以为任务下达和后续的工站任务序列迭代优化提供支持，进而为准时化生产目标的实现提供支撑。

4 工站任务的序列迭代优化

包装线下属的工站在执行工序任务时，经常会遇到多个工序任务积压，形成待执行的工站任务序列。由于各种异常状况（如交付期变动、紧急任务插单等）时有发生，需要将本工站的任务序列数据、与本工站的任务序列相关联的上下游工站的具体数据等作为优化背景条件，对工站上待执行的工序任务进行序列优化。

为了快速得到优化结果，依据工序任务交付期的先后截取前几项工序任务进行序列优化，将更新后的工序任务交付期与初始状态进行比对，如果有一定的偏离，则通过规则判断能否通过局部序列调整解决，对于能够通过局部序列调整处理的异常，采用迭代算法对工序任务序列进行优化调整；对于无法通过局部处理解决的问题，则需提交给上层管理决策系统进行处理。

4.1 工站任务序列优化的数学表示

包装工站任务序列迭代优化的运作机理可描述为：根据工站的待执行工站任务序列中各工序任务所属包装线任务的优先级，同时考虑工序任务提前完成的惩罚与滞后完成的惩罚，以最小化加权总提前时间和总滞后时间为优化目标，基于初始状态，采用启发式算法对工站的前若干项工序任务形成的待执行工站任务序列的顺序进行便捷的调整，同时更新工序任务的开始时间与完工时间，从而实现对工站任务积压及异常状况的快速反应。

用ptij表示某工站承担包装线任务Ti的第j个工序任务，相关符号的含义如下：

●WorkingHoursj：工序任务ptij的工时；

●DeliveryTimej：工序任务ptij的交付期；

●BeginTimej：工序任务ptij的开始时间；

●ActualEndTimej：工序任务ptij的实际结束时间；

●pti（j-1）：工序任务ptij的紧前工序；

●pti（j+1）：工序任务ptij的紧后工序；

●LeadTimej=max｛DeliveryTimej-ActualEndTimej，0｝：工序任务ptij的提前时间；

●LaggingTimej=max｛ActualEndTimej-DeliveryTimej，0｝：工序任务ptij的滞后时间；

●ξ1：提前惩罚因子；

●ξ2：滞后惩罚因子；

●IntervalTime（j，j+1）=StartTimej+1-ActualEndTimej：工序任务ptij的结束到工序任务pti（j+1）开始之间的间隔时间；

●Ωj：表示工序任务ptij向后移动一个单位时惩罚的变化。

因此，工序任务ptij的交付期可表示为：DeliveryTimej=max｛ActualEndTimej-1+WorkingHoursj，BeginTimej+1｝。当工序任务ptij没有紧前工序时，ActualEndTimej-1=0；当工序任务ptij没有紧后工序时，BeginTimej+1=0。对于工序任务队列中的两个工序任务ptij、ptuk，其中，ptij从属于整机任务tE，ptuk从属于整机任务，可以推断出：如果（ActualEndTimej-1≤ActualEndTimek-1）∧（DeliveryTimej≤DeliveryTimek），那么ptij应排在ptuk的前面。实际上，工序任务ptij的ActualEndTimej-1和StartTimej+1都可能会发生相应改变，使其交付期DeliveryTimej与初始状态的交付期DeliveryTimej*有一定偏离，这个偏离量可表示为。对于待优化的工序任务序列PTS=｛ptij，…｝（即工站的前若干项工序任务），考虑工序任务所属的包装线任务优先级，可得PTS中工序任务交付期的加权偏离度wd为：

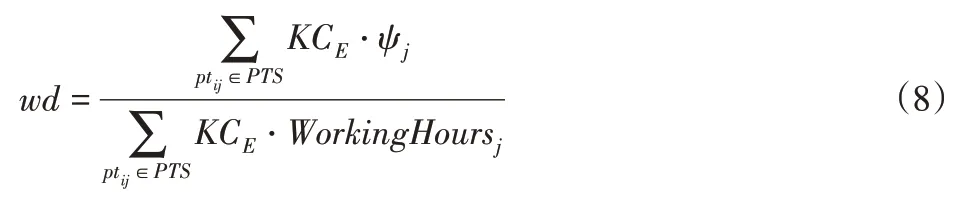
式中：KCE—工序任务ptij所属的包装线任务tE的优先级；Ψj—工序任务ptij的交付期DeliveryTimej与初始状态的交付期的偏离量；WorkingHoursj—工序任务ptij的工时。根据加权偏离度wd来判断是否进行包装工站任务序列的迭代优化，若wd超过设定的峰值时，则超出这里所提出方法的处理范围，应由更高级别的管理人员进行处理。

包装工站任务序列迭代优化通过尽可能地降低工站中待执行的每项工序任务的提前完工量和滞后完工量，从而促进按期交付目标的实现。故而，以加权总提前时间和加权总滞后时间的最小化为目标，目标函数如下：

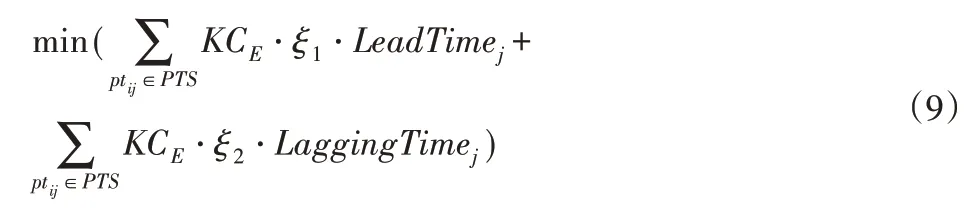
式中：LeadTimej和LaggingTimej—工序任务ptij的提前时间和滞后时间。

为确保同工序任务必须在其紧前工序完成后才能开始，且工序任务执行过程中工站不允许被其他工序任务抢占，限定的约束条件为：（1）ActualEndTimej-ActualEndTimej-1≥WorkingHoursj；（2）（ActualEndTimej-ActualEndTimek≥WorkingHoursj）∨（ActualEnd-Timek-ActualEndTimej≥WorkingHoursk）。

4.2 工站任务序列迭代优化的具体步骤

具体的包装工站任务序列迭代优化步骤如下：

（1）获取工站的前p项待执行工序任务作为需要优化的工序任务序列PTS=｛ptij，…｝，根据ActualEndTimej-1和StartTimej+1更新DeliveryTimej，按DeliveryTimej大小进行排序。

（2）计算PTS 中工序任务交付期的加权偏离度wd，判断能否通过局部序列调整来解决问题。这里偏离度上限设定为15%（由管理者设定，可根据实际情况进行调整），当偏离度超过15%时，提交给上层决策系统进行处理，流程结束；否则继续（3）。

（3）如果（ActualEndTimej-1≤ActualEndTimek-1）∧（Delivery-Timej≤DeliveryTimek），那么在工序任务序列中ptij应排在ptuk的前面。依此生成工序任务序列集合｛PTS1，PTS2，…｝，确定每个序列的任务开始时间：

①依据目标函数的两个约束条件，以每项任务的最早可开始时间作为初始开始时间。

②求解每项工序任务的LeadTimej和LaggingTimej，在不考虑开始时间固定的任务的情况下，搜索工序任务序列中第一个LeadTimer＞0的任务r，并找出距离该工序任务最近的时间间隔IntervalTime（s，s+1），r≤s≤p。

④对任务r，r+1，…，s的开始时间增加min｛LeadTimer，Lead-Timer+1，…，LeadTimeu，IntervalTime（s，s+1）｝，转②。

（4）按照（3）中生成的工序任务序列集合｛PTS1，PTS2，…｝、每个队列的任务开始时间以及队列中各工序任务所属包装线任务的优先度，求解目标函数值，则目标函数值最小的序列即为最优序列，迭代优化过程结束。

5 实例验证

5.1 卧式钢卷半自动化包装线任务的优先级评定

对于某钢铁企业的卧式钢卷半自动化包装车间，已知条件如下：

（1）该车间承担着卧式钢卷的包装生产任务，包括三种生产类型：大量、成批、小批量，其模糊评估值依次为0.8333、0.6667、0.3333；

（2）承担卧式钢卷包装生产任务的包装线共有三条：PL1、PL2、PL3，承载极值依次为5、10、8，当前任务承载依次为3、7、4，单位为个。不同类型的任务在三条包装线上混合执行；

（3）用户包括甲公司、乙公司和丙公司，即三种生产类型，其模糊评估值依次为0.7500、0.5000、0.2500；

（4）卧式钢卷的包装工艺包含9个工序，依次对应9个工站，如图4所示。

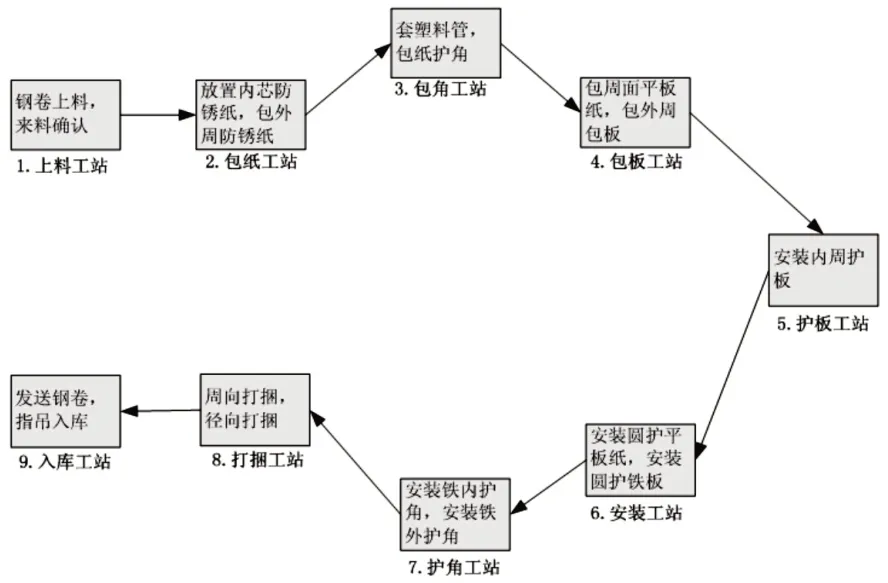
图4 卧式钢卷的包装线及各工站对应的工序Fig.4 Packaging Line of Horizontal Steel Coil and Corresponding Procedure of Each Work Station

某订单计划中有5个任务T1、T2、T3、T4、T5，对应生产线依次为PL2、PL1、PL3、PL3、PL1，其指标值，如表1所示。

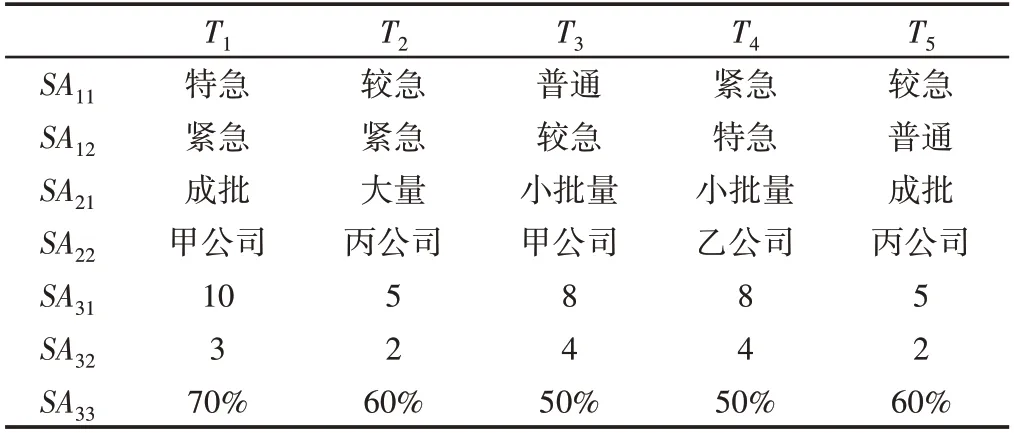
表1 某订单计划中5个任务的指标值Tab.1 Indicator Values of Five Tasks in an Order Plan

以目标O为准则，以SA1中元素SA1，2为子准则，基于SA3中元素对SA1，2的影响力大小，采用专家评价法进行SA3中元素的间接优势比较。设专家给出的评判矩阵为：

该矩阵一致性检验合格，在Matlab中解出其对应于最大特征值的特征向量为ω3，(1，2)=[0.9161，0.3715，0.1506]T，标准化后为ω3，(1，2)=[0.6370，0.2583，0.1047]T。由于SA3中元素对SA1，1没有影响，故ω3，(1，1)=[0，0，0]T，于是：

同理求得其他矩阵子块，得到控制层元素O下的超矩阵Ω：

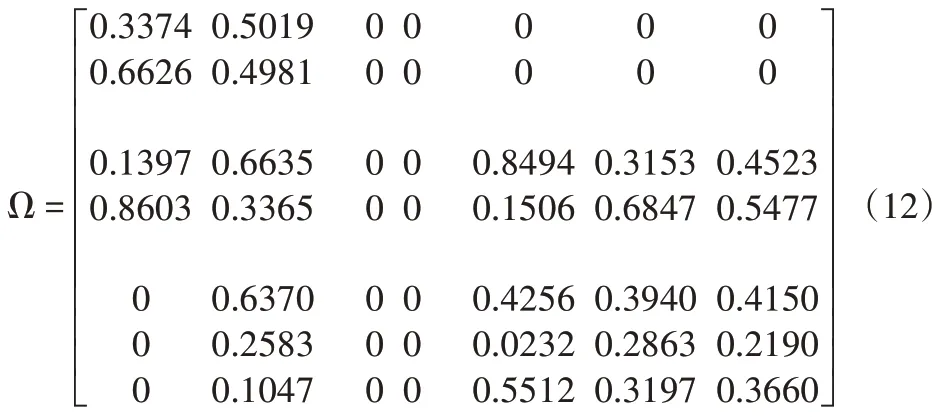
此时，矩阵Ω中的子块Ωi，j已进行列标准化，但Ω尚未列标准化。为解决此问题，同理得到元素组SA1，SA2，SA3的相对重要度矩阵Ψ=(ψi，j)3×3：

由表1可得，指标值矩阵为：

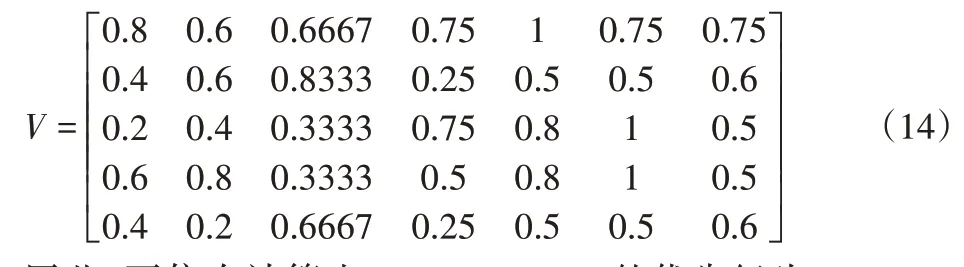
因此，可依次计算出T1、T2、T3、T4、T5的优先级为：0.7527，0.5457，0.6369，0.6553，0.4842。因此，T1的优先级最高，T5的优先级最低，按从高到低排序为：T1＞T4＞T3＞T2＞T5。

5.2 打捆工站任务序列的迭代优化

在该钢铁企业的卧式钢卷半自动化包装车间，某条包装线的打捆工站当前要执行的工序任务实时信息，如表2所示。从表2中获取前6项工序任务，根据DeliveryTimej=max｛ActualEndTimej-1+WorkingHoursj，StartTimej+1｝来更新每项任务的交付期。前6项工序任务所属包装线任务的优先级由第2章计算出，依次为：0.7961，0.2789，0.8958，0.6953，0.3029，0.1765，经归一化处理后为：0.2531，0.0887，0.2848，0.2210，0.0963，0.0561。计算前6 项工序任务的加权偏离度wd=13.42%＜15%，因此能够通过局部序列调整来解决问题。

表2 打捆工站当前要执行的工序任务实时信息Tab.2 The Process Task Real-Time Information to Be Executed by the Bundling Workstation

对于表2中的前6项工序任务，生成的工序任务序列包括：

●PTS1=1，2，3，4，5，6；

●PTS2=1，2，3，5，4，6；

●PTS3=1，3，2，4，5，6；

●PTS4=1，3，2，5，4，6。

求解出每个序列中任务的开始时间分别为：2，20，28，40，49，59；2，20，28，40，50，59；2，13，25，36，45，55；2，13，25，33，43，52。

为简化计算，认为提前惩罚因子ξ1与滞后惩罚因子ξ2相等，算得目标函数值依次为：12.0971，13.7906，8.3125，4.5837，那么目标函数值最小的工序任务序列PTS4=1，3，2，5，4，6即为当前的最优工序任务序列。

这里，PTS1实际上就是初始状态，优化后的结果PTS4与初始状态PTS1相比，目标函数值大大降低，故而有利于该工站按时交付目标的实现。卧式钢卷半自动化包装线属于典型的离散型半自动化混流包装线，通过在该包装线的应用实施说明这里提出的生产任务管控框架适用于离散型半自动化混流包装线的任务管控。

6 结语

这里建立了基于工艺任务优先级评定和工序任务序列优化的离散型半自动化混流包装线生产任务管控框架。面向包装线级，依据属性的关联支配关系建立了包装线任务优先级评定层次化模型，给出了指标值求解方法；采用ANP来确定指标权重，根据指标值和指标权重获得包装线工艺任务的优先级数值，为任务下达提供决策支持，在生产过程中对优先级高的包装线工艺任务应给予适度的资源调配倾斜。面向工站级，针对工站的多个工序任务积压及突发异常等问题，提出了一种考虑包装线工艺任务优先级的工序任务序列迭代优化算法，以最小化加权总提前时间和总滞后时间为优化目标，求解当前最优工序任务序列，可在一定程度上提升工站的按期交付能力。

相比传统调度理论及相关算法，这里从离散型半自动化混流包装线管控的实际业务需求出发，能够为制造资源配置的优化、准时交付能力的提升提供一种可行的解决方案。