SiO2粒径大小对浆料直写陶瓷浆体的流动影响研究

张 捷，顾 海，姜 杰，孙健华

（1.南通理工学院机械工程学院，江苏 南通 226002；2.江苏省3D打印装备及应用技术重点建设实验室，江苏 南通 226002）

1 引言

陶瓷材料作为一种常见无机非金属材料，因其较为出色的稳定性、抗腐蚀及耐高低温等特点，被广泛应用于各工业领域，其中SiO2材料即为一种典型的陶瓷材料。近些年出现的浆料直写技术为成型SiO2陶瓷材料提供了新的工艺方案［1-3］。在前期研究中发现，材料的诸多参数将影响成型工艺过程，如对浆体在挤出装置中流动的影响。因此材料参数对流动过程影响的研究也显得尤为必要，其中，颗粒大小就是重要影响因素之一，将着重探讨SiO2粉末材料颗粒大小对配制浆体在挤出装置中的流动的影响。

文献［4-5］对流体流动进行分析时，较为常见的方法是利用Fluent及Polyflow等有限元软件，文献［6］利用Fluent对单螺杆中的流体流动进行了模拟；文献［7］利用有限元对造纸废料在单螺杆中的流动进行了分析；文献［8］利用Polyflow对PLA在单螺杆挤出机中的熔融输送段进行了模拟。利用软件求解时，过程复杂，尤其是针对陶瓷混合浆体类的非牛顿流体［9］，仿真的稳定性和结果的准确性将会受到影响，而介观方法LBM具有求解过程简单，计算过程清晰，易于实现的特点，避免了对复杂微分方程的求解，目前已在流体领域得到了较多的应用［10-11］，文献［12］利用MRT LBM对水泥浆体在3D打印过程中的基础环节进行了分析；文献［13］利用LBM对幂律流体在单螺杆挤出机中的流动进行了分析。

以SiO2陶瓷粉末为原材料，针对浆料直写陶瓷3D打印工艺，将选用单螺杆挤出机作为浆体的挤出装置，为了确保数值模拟过程的稳定性和准确性，在传统LBM基础上提出修正方法，并结合MATLAB软件对不同颗粒大小SiO2的浆体在螺槽内的流动进行分析，以揭示SiO2粉末粒径大小对流动过程的影响规律。

2 颗粒大小对浆体流变性能的影响

在制备陶瓷浆料时，选用SiO2粉末为陶瓷材料，且SiO2粉末将选用三种不同粒径进行对比，分别为纳米级，亚微米级以及微米级其中纳米级的二氧化硅粉末为德国Degussa AG公司生产的Aerosil OX50，颗粒的粒径范围为（40～80）nm；亚微米级的二氧化硅粉末为美国Alfa Aestar 公司生产，颗粒的平均粒径大小为0.25μm；微米级的二氧化硅粉末为日本Tokoyama公司的Excelica，颗粒的平均粒径大小为3μm。上述三种不同粒径的SiO2粉末的粒径分布图，如图1所示。

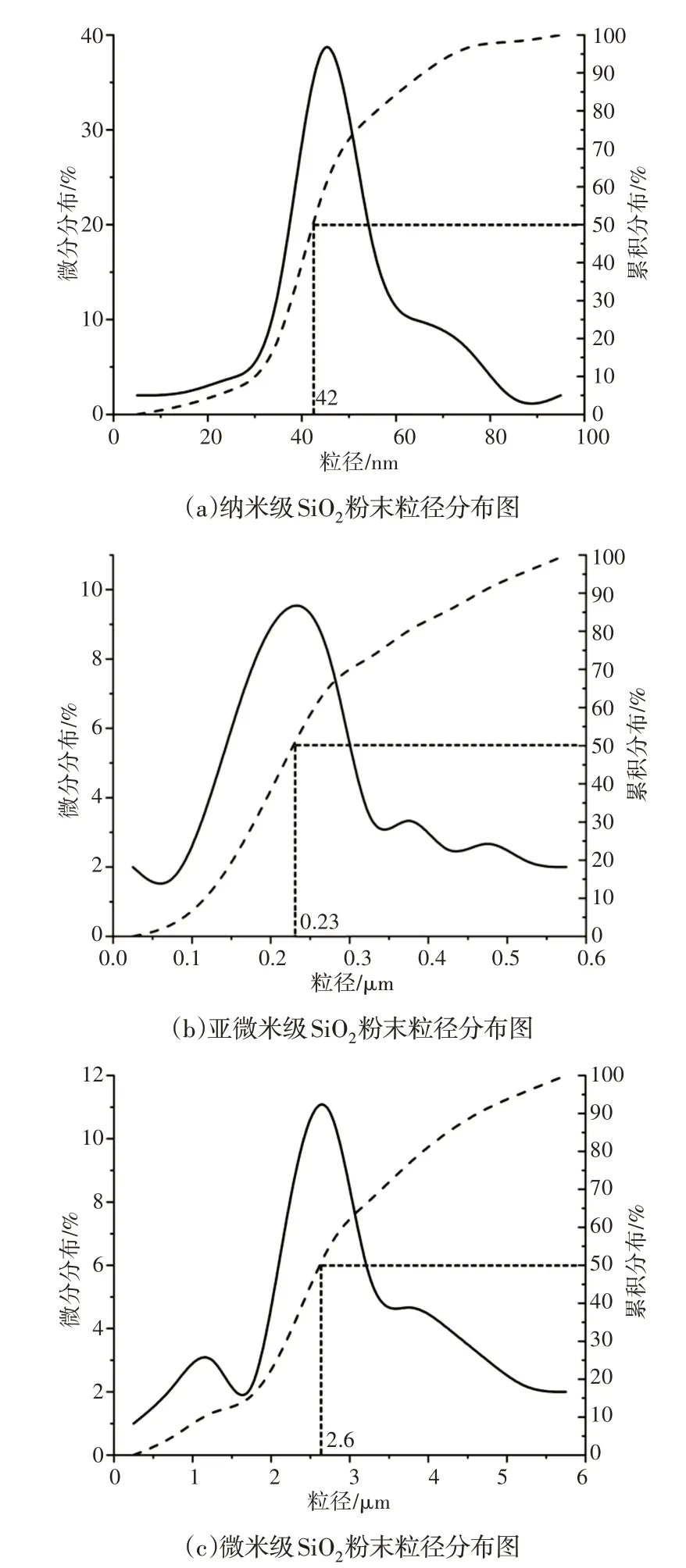
图1 SiO2粉末的粒径分布图Fig.1 Particle Size Distributions of SiO2 Particles

在配制浆体时，材料的配比方案为SiO2陶瓷粉末的质量分数为50%（三种粒径SiO2陶瓷粉末的质量分数相同，保证固相含量一致，仅粒径不同），甲基丙烯酸甲酯的质量分数为15%，季戊四醇三丙烯酸酯的质量分数为33%，苯偶酰的质量分数为2%，其中，季戊四醇三丙烯酸酯、苯偶酰以及甲基丙烯酸甲酯作为有机溶剂，混合后均匀加入SiO2粉末，同时高速搅拌帮助粉末迅速溶解，最终获得备用浆体。制得浆料后，需要对其密度和粘度进行测试，以获取其流变方程以及为后续数值模拟分析做准备，经测量三种不同粒径SiO2粉末制成的浆体的密度分别为2.14g/cm3（纳米级），2.89g/cm3（亚微米级），2.66g/cm3（微米级）。

利用旋转粘度计（型号为Rheolab MC1）对混合浆体的进行了流变实验，结果表明浆料呈现出明显剪切变稀的非牛顿特征，根据MATLAB 软件拟合结果，三种浆体的流变方程均趋向于幂律流体种类，经整理后拟合结果和流变测试数据，如图2 所示。具体的流变方程分别为：

图2 不同粒径SiO2浆体的流变分析结果Fig.2 Rheological Analysis of SiO2 Slurry with Different Particle Sizes

式（1）～式（3）分别对应的是微米级、亚微米级及纳米级SiO2粉末制成浆体的流变方程。

3 幂律流体的修正LBM

对于非牛顿流体，利用标准的LBM进行仿真时，极易出现发散的情况，导致模拟仿真的失败。为了保证模拟过程的稳定性，提出一种修正LBM，以含外力项的传统LBM为基础，将幂律流体的非牛顿特性看成一种特殊的外力项。标准含外力项的LBM分布函数f方程，如式（4）所示。

式中：τ—松弛时间；r—位移；t—时间，D2Q9模型的速度配置矢量ei的具体描述，如式（5）所示。

在式（4）中，第i项的外力分项Fin的计算公式为：

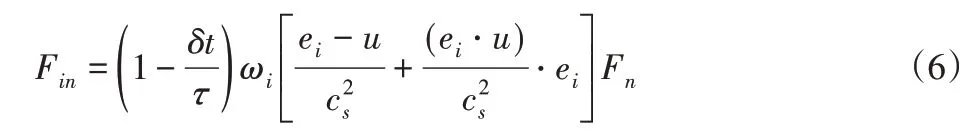
式中：δt—时间步长，一般取1，宏观物理量速度矢量u，密度ρ可以根据平衡态分布函数以及格子声速获得，具体如下式所示：

这里选用LBM 中常见的D2Q9 模型，因此，格子声速cs=，权重参数ωi的具体形式，如式（9）所示。

根据各向同性约束条件，可以获得：

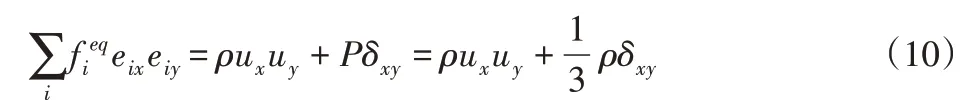
式中：δxy—克罗内克函数。

基于Chapman-Enskog的展开形式，分布函数和动量张量可以扩展为：

对于诸如Herschel-Bulkley流体之类的非牛顿流体，应变率张量Sxy的计算公式，如式（15）所示。

动力粘度ν与运动粘度μ、松弛时间τ和密度ρ的关系如下。

那么，根据式（13）～式（16）可以将式（12）转换为：

对于不可压缩流体，动量张量也可以通过下式计算获得。

由式（12）～式（18），应力张量σxy可以推导获得：

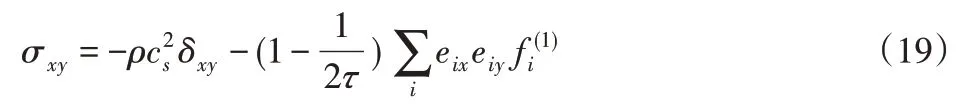
根据式（15），应变率张量的第二不变量DII可以由下式计算获得：

其中，维度l=2.那么剪切率即可通过下式获得：

综上所述，对非牛顿流体进行LBM数值模拟时将受到松弛过程的影响，因此仿真计算的稳定性和准确性将受到非恒定粘度的影响，而粘度主要通过剪切率计算后获得。当剪切率接近于0时，剪切变稀型流体粘度趋向于无穷大，这将引起计算的发散，而剪切增稠型流体粘度将趋向于0。为了解决上述问题，将针对式（4）中的外力项进行改进，用以描述幂律流体的非牛顿特性。结合式（15），式（19）可改进为，如式（22）所示。

根据Navier-Stokes方程在不可压缩极限下的Chapman-Enskog展开，可获得式（23）：

进一步化简可以得到，

将上式代入式（6）可得，

4 SiO2陶瓷浆体的流动及对比分析

4.1 单螺杆挤出机的结构

以单螺杆挤出机作为此处浆体的挤出装置，单螺杆的结构，如图3所示。为了便于分析，将螺杆结构沿螺槽方向充分展开，即可获得截面为矩形的流动通道，如图4所示。具体结构参数，如表1所示。

表1 螺杆的关键几何参数Tab.1 Key Geometrical Factors of Screw Extruder

图3 螺杆结构Fig.3 Structure of Screw Extruder

图4 螺杆展开结构Fig.4 Expanded Structure of Screw Extruder

4.2 修正LBM模拟分析流程

在第2部分，对修正LBM进行了详细介绍，结合MATLAB可以编程实现对幂律型陶瓷浆体进行流动分析，具体的分析计算步骤如下：

（1）确定物理模型的主要基本参数，如计算域（挤出装置的结构尺寸）、初始速度（由转速决定）以及密度（参考上述实验测定结果）等；

（2）根据式（8）计算并确定平衡态分布参数；

（3）根据式（21）计算应变率张量；

（4）结合式（1）～（3）获得的浆体的流变方程以及式（16）计算获得当前计算循环步内的松弛时间τ；

（5）根据式（4）和式（25）计算当前的分布函数，选择非周期性边界条件进行边界处理［14］；

（6）根据式（7）计算密度和速度；

（7）返回第（3）步执行下一次循环计算。

4.3 SiO2陶瓷浆体在挤出机中的流动分析

以纳米级SiO2陶瓷粉末制成的陶瓷浆体在挤出机中的流动分析为例给出仿真后的结果。取图4中的Y-Z组成的截面，根据螺杆挤出的实际运动，将速度仅设定在与Z方向一致的上表面，根据螺槽的几何尺寸，设置模拟时的格子数为（200×100），螺杆的转速设定为N=40r/min。利用上述提出的修正LBM 进行数值模拟，流线图，如图5所示。观察后发现流动主要集中在两螺棱中心位置且靠近外筒内壁面的位置，流动中心的具体位置为（0.5W，0.72h），在贴近螺棱角落的位置，几乎不存在浆体流动。因此在设计螺棱时，靠近螺柱部分的厚度可大于靠近螺筒部分的厚度。在对亚微米级及微米级陶瓷浆体进行仿真时，具有类似的流线图分布情况，主要区别是流动中心的位置有所差异，具体中心位置，如表2所示。当SiO2粉末粒径越大时，浆体流动更贴近于外筒的内壁面。水平速度分量u沿螺槽两向的分布的情况，如图6、图7所示。其中速度分量u沿螺槽宽度方向的分布情况，如图6所示。速度分量u沿螺槽深度方向的分布情况，如图7所示。由图可知，在不同螺槽深度时，速度差异较大，靠近外筒内壁面的速度较大，而贴近螺杆表面的速度则相对较小且趋近于0，且在两螺棱相对中间的位置将保持相对平稳的速度流动。

图5 浆体在Y-Z截面的流线图Fig.5 Streamlines Figure of the Paste in the Section Y-Z

表2 不同粒径下的浆体流动中心位置的对比Tab.2 Comparison of the Central Point of the Slurry Flow with Different Particle Sizes

图6 速度分量u沿螺槽宽度的分布Fig.6 Distribution of Velocity u along Screw Width

图7 速度分量u沿螺槽深度的分布Fig.7 Distribution of Velocity u along Screw Depth

垂直速度分量v沿螺槽两向的分布的情况，如图8、图9所示。其中，速度分量v沿螺槽宽度方向的分布情况，如图8所示。速度分量v沿螺槽深度方向的分布情况，如图9所示。由图可知，在不同螺槽深度时，垂直速度分量差异明显，靠近外筒内壁面的速度较大，而贴近螺杆表面的速度则相对较小且趋近于0，从螺槽宽度看，两螺棱中间位置垂直速度为0。为了进一步对比三种不同粒径下的SiO2浆体对流动情况的影响，对三种情况均进行了分析，取螺槽宽度为5mm，螺槽深度为3.5mm 处以及螺槽宽度为3.5mm，螺槽深度为5mm 处的速度分量进行对比结果，如表3所示。根据表中结果可以发现，颗粒粒径越小时，越有利于浆体的流动，因此从浆体流动性角度考虑，在满足其他打印条件下选用较细的SiO2粉末更好。

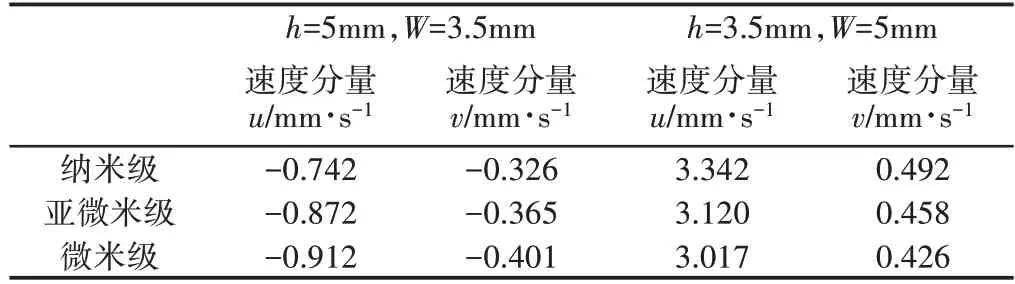
表3 流动速度对比结果Tab.3 Comparison of Flow Velocity

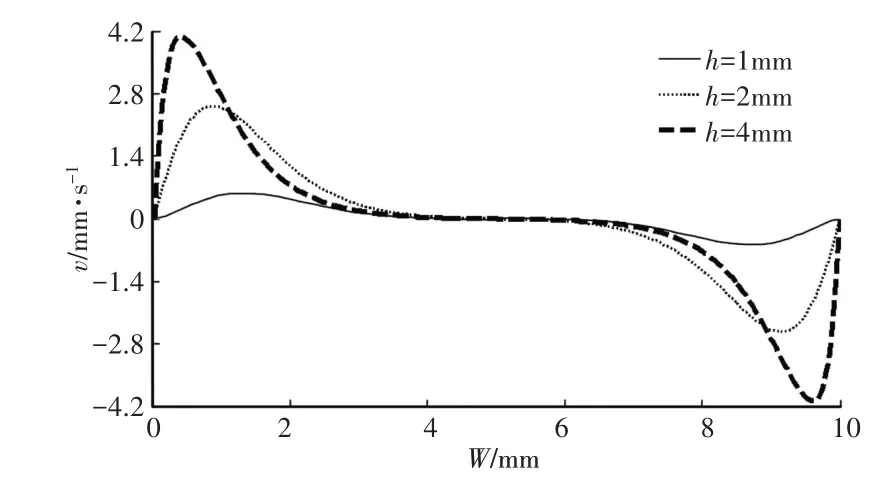
图8 速度分量v沿螺槽宽度的分布Fig.8 Distribution of Velocity v along Screw Width

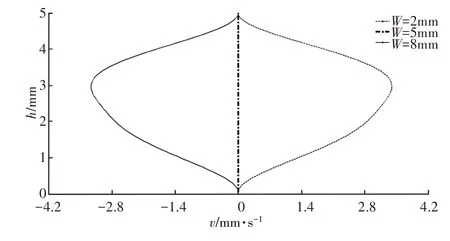
图9 速度分量v沿螺槽深度的分布Fig.9 Distribution of Velocity v along Screw Depth

5 结论

针对浆料直写陶瓷3D打印工艺，探讨了不同颗粒大小对陶瓷浆体在挤出装置中流动时的影响，以纳米级SiO2粉末为例，提出了修正LBM，并对浆体在螺槽中的流动进行了数值模拟分析，最后综合对比了三种相同固相含量不同粒径SiO2粉末制备的陶瓷浆体在挤出机中流动情况，可以获得以下结论：（1）作为介观方法，修正LBM可有效用于非牛顿性的SiO2陶瓷浆体流动中，仿真过程稳定，可有效避免发散的结果，保证数值模拟过程的稳定性。（2）数值模拟的结果证明，SiO2粉末的颗粒大小对浆体流动有显著影响，粒径较小的纳米级SiO2粉末制备的浆体更有利于其在挤出机中的流动，究其主要原因是不同粒径的SiO2粉末制备所得的浆体呈现出了不同的流变特征及密度等重要物理特性，使最终的流动也呈现出不同的特征，从流体力学角度解释了粒径较小的粉末能改善流动性能的原因。（3）流动结果还表明，浆体的流动主要集中在流道（螺槽）的中部，因此可以适当增加螺距，改善流动速度，尤其是对于粒径较大粉末制备的浆体；其次在流道的左右下角均无明显流动，螺棱的厚度在越靠近螺柱时适当增大，使螺棱与螺柱之间形成一倾角，可以改善强度，提高力学性能。