基于双层全局灵敏度分析的车辆系统响应特性研究及验证
王振峰 严格 杨建森 李洪亮 田阳
(1.中汽研(天津)汽车工程研究院有限公司,天津 300300;2.柳州五菱汽车工业有限公司,柳州 545000;3.燕山大学,秦皇岛 066004)
主题词:车辆动力学 灵敏度分析 响应特性 耦合车辆模型
1 前言
车辆动力学模型是自动驾驶算法、车辆动力学控制算法、底盘/悬架控制算法的核心基础,其关键参数对深入分析底盘性能优劣与车辆系统响应特性有较大影响,研究模型关键参数对车辆系统的响应特性不仅有利于缩短车辆新技术的开发时间,且可有效降低开发成本[1-2]。在当下日益复杂的交通环境和驾驶场景(如转弯制动、障碍物紧急避障与路径跟踪等[3-5])输入工况下,采用非耦合或单车模型的车辆动力学控制很难实现令人满意的底盘操纵稳定性与乘坐舒适性。与此同时,如何在控制器开发中设计快速高效的基于耦合车辆模型的集成控制方法成为该领域的研究热点与难点[6-7]。
车辆核心参数对车辆系统瞬态与稳态动态响应有很大影响,深入研究车辆系统关键参数与系统响应之间的对应关系,将有助于更好地理解车辆动态响应及其底盘集成控制。灵敏度分析(Sensitivity Analysis,SA)被认为是基于量化参数对系统输出响应特性物理描述的有效方法[8-9]。
本文基于双层全局灵敏度分析(Global Sensitivity Analysis,GSA)方法研究车辆系统参数与响应之间的关系,提出一种新的双层全局灵敏度分析方法,以减少蒙特卡罗技术带来的高计算量。以整车横向-纵向耦合的非线性车辆模型作为分析对象,并在不同转向盘转角与路面激励复合输入工况下对所提出的GSA方法进行验证。
2 整车垂向与横向动力学建模
2.1 车辆系统运动学分析
为了获得整车垂向与横向动力学函数关系,建立包含车辆的侧倾运动、车身俯仰运动、车身垂向运动、横向运动、横摆运动以及4 个轮胎的垂直运动的整车9自由度模型,如图1 所示。其中:a、b分别为车辆质心与前、后轴的距离;δfl、δfr分别为车辆左、右前轮转角;αf、αr分别为前、后轮侧偏角;lt为轮距;x、y分别为车辆纵、横向运动距离;vx、vy分别为车辆质心纵、横向速度;ci、ksi分别为各轮悬架阻尼、垂向刚度;kti为各轮轮胎刚度;zb、zwi分别为车辆质心的垂向位移、各轮非簧载质量的垂向位移;M、ms、mwi分别为车辆总质量、簧载质量、各轮非簧载质量;zri为各轮路面激励位移;hroll为车辆侧倾中心与质心间的距离;Ix、Iy、Iz分别为车辆侧倾、俯仰、横摆转动惯量;Cf、Cr分别为车辆前、后轮侧偏刚度;φ、θ分别为车辆簧载质量侧倾角、俯仰角;ω为车辆簧载质量横摆角速度;ay为车辆侧向加速度;Fy1、Fy2、Fy3、Fy4分别为车辆左前、右前、左后、右后轮轮胎侧向力。
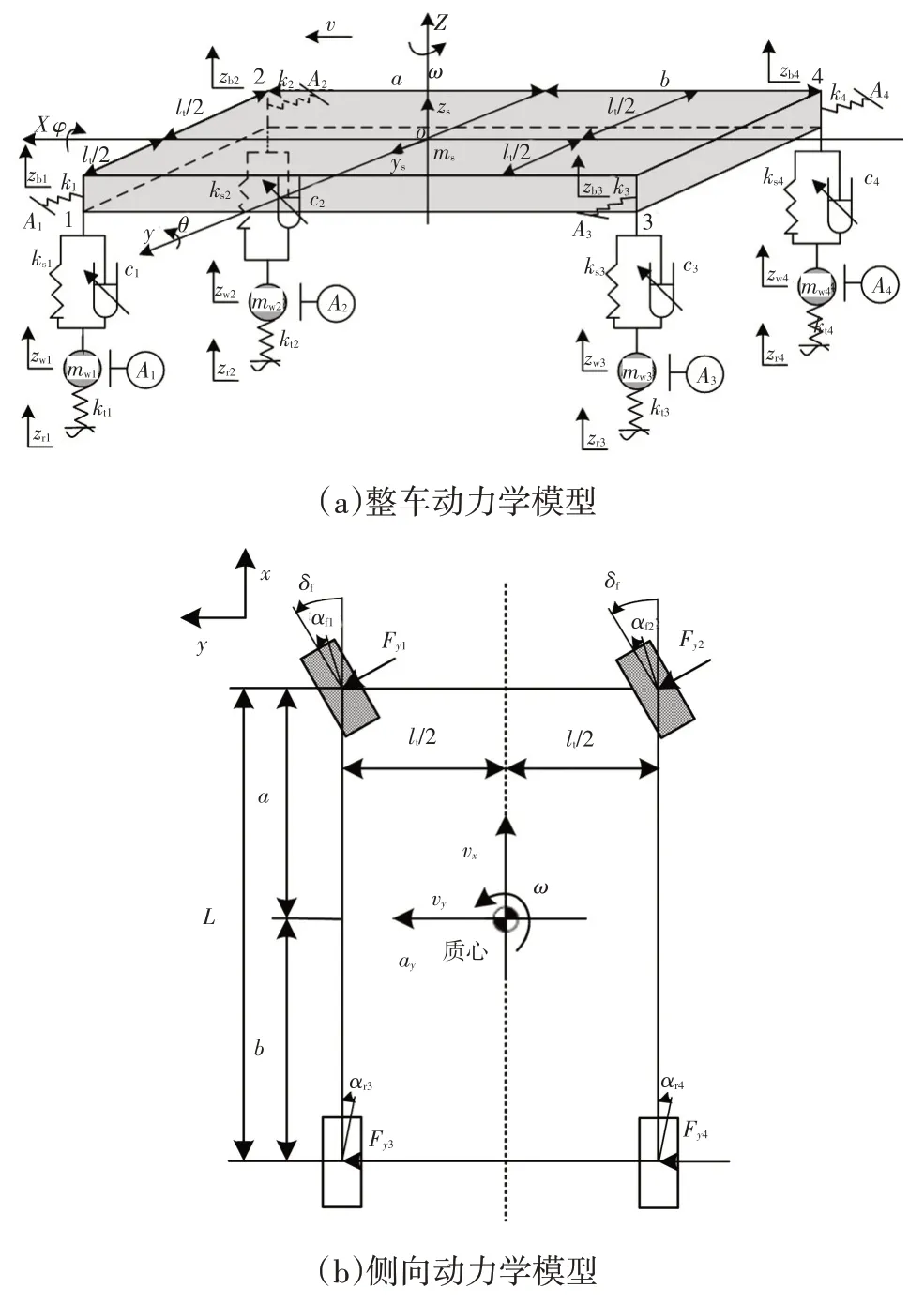
图1 9自由度整车模型
在车辆参考坐标系Sv中,簧载质量质心位置为:

且
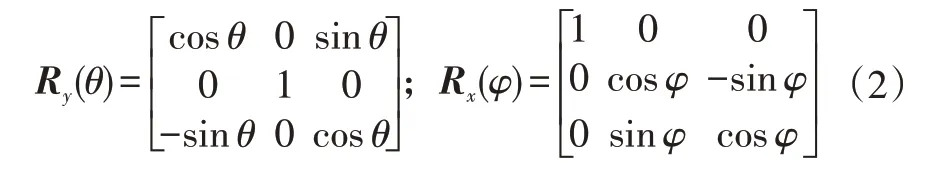
故地面坐标系G与车辆坐标系v之间的关系为:
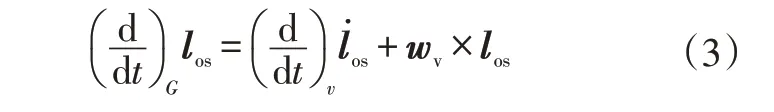
式中,wv=[0 0ω]T为旋转运动矢量;Rx、Ry分别为绕X轴、Y轴的极坐标;为车辆质心位置的偏导。
车辆相对地面固定坐标系SG的质心速度vs可以用相对车辆坐标系的车辆速度vv与los表示:
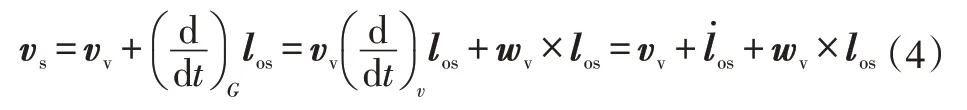
与此同时,相关的簧载质量加速度、非簧载质心相对位置及其相对的旋转运动可分别表示为:
a.车辆簧载质量加速度as相对坐标系SG的计算公式为:
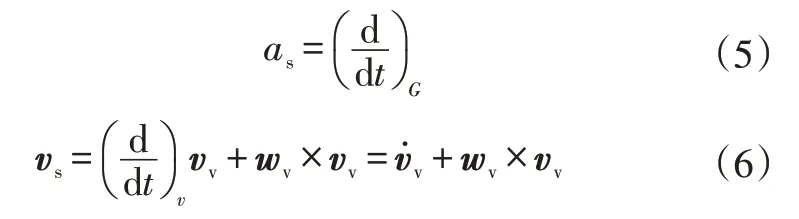
b.车辆非簧载质量质心的转移。利用车辆簧载质量质心转移方法,非簧载质量质心相对坐标系Sv的转移可表示为:

式中,lwi为非簧载质量质心转移矩阵。
c.车辆簧载与非簧载质量质心的旋转运动。簧载质量的旋转角动量Ds可表示为:
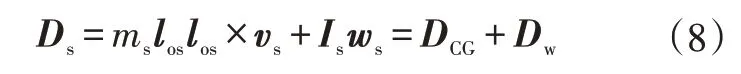
式中,DCG为质心角动量;Dw为非簧载质量角动量。
同时,非簧载质量角动量Dw可表示为:

式中,wi、vi分别为旋转与直线运动速度矢量。
2.2 轮胎建模
Pacejka[10]提出的“魔术公式”可以很好地描述轮胎横向非线性特性:
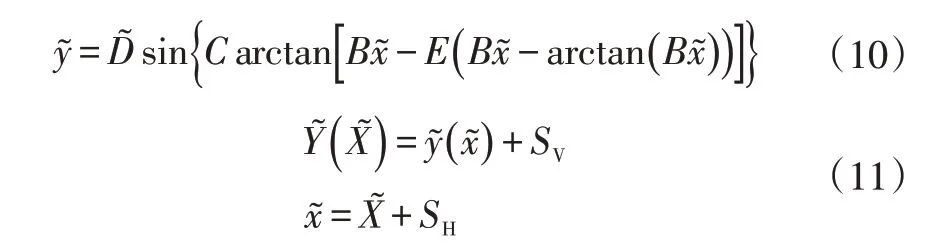
式中,高高高高为输入状态,主要指滑移率或侧偏角;高高高高为输出量,主要指横向力、纵向力或回正力矩;影响因子B、C、、E分别为试验拟合曲线的斜率、试验曲线的形状、峰值、曲率,可从试验数据中获取;SH、SV分别为输入与输出状态的补偿量。
2.3 整车模型
由牛顿第二定律以及图1所示的整车9自由度动力学模型可知,针对整车的不同运动,有:
a.车辆簧载质量垂向运动方程为:

式中,Fsi为第i个簧载质量悬架作用力;为簧载质量总的垂向加速度。
Fsi可表示为:
同时:
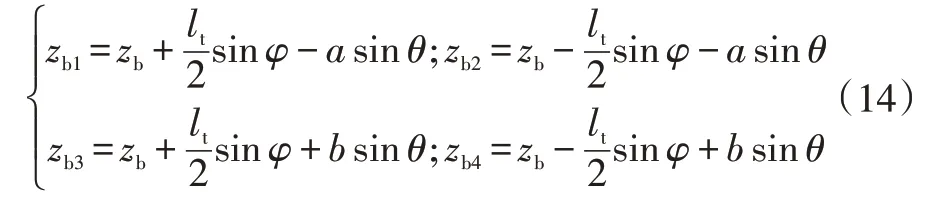
b.车辆非簧载质量垂向运动方程为:

式中,Fwi为第i个非簧载悬架作用力;为非簧载质量总的垂向加速度。
Fwi可表示为:

同时,整车左前轮、左后轮、右前轮、右后轮对应的垂向轮胎力可分别表示为:
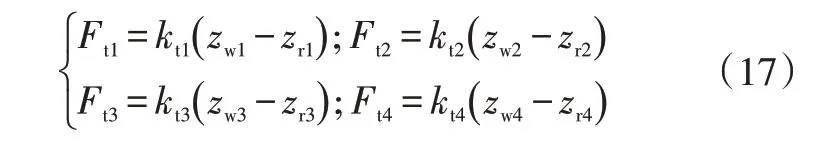
c.车辆俯仰运动方程为:
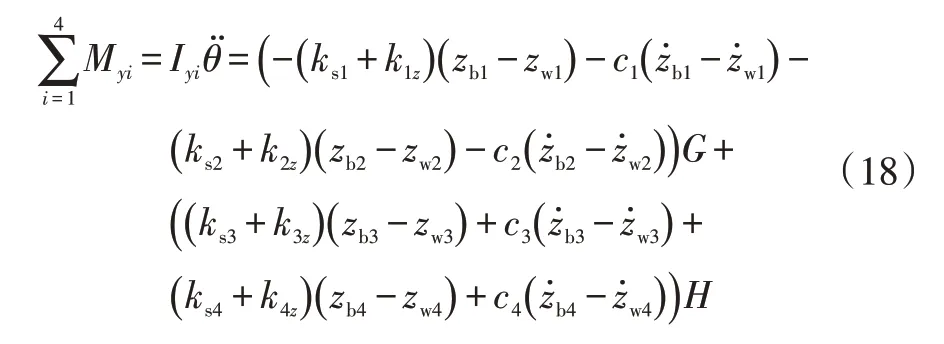
式中,Myi、Iyi分别为车辆不同i位置对应的俯仰力矩和俯仰转动惯量;kiz为车身与悬架系统不同接触位置弹簧刚度的垂向分量;G、H为关于俯仰运动的函数。
d.车辆侧倾运动方程为:

式中,Mxi、Ixi分别为车辆不同位置i的侧倾力矩和侧倾转动惯量;kiz为车身与悬架系统不同接触位置i的弹簧刚度的垂向分量。
e.车辆横向运动方程为:
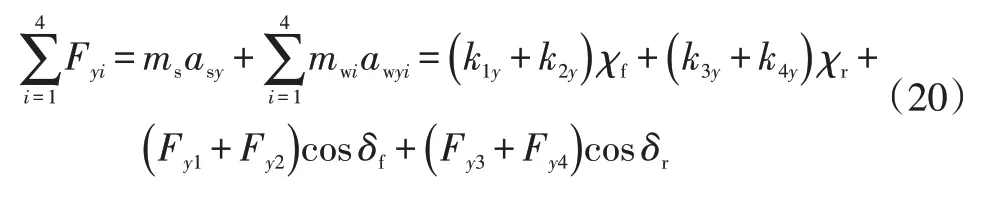
式中,Fyi为车辆转向离心力所产生的车辆不同位置横向力;kiy为车身与悬架系统不同接触位置弹簧刚度的横向分量;χf、χr分别为俯仰、侧倾相关的函数,是车身对应位移变量;asy、awyi分别为簧载质量横向加速度、非簧载质量横向加速度;δf、δr分别为前、后轮的转向角。
f.车辆横摆运动方程为:

式中,Mzi、Izi分别为车辆不同位置横摆力矩和横摆转动惯量;为车身与悬架系统不同接触位置的横向力矩。
3 系统全局灵敏度筛选理论
针对复杂多变量系统输入工况,由于无法较好地获取系统关键参数以及常规参数之间的内在耦合关系,导致无法对系统响应特性进行定量研究。为有效解决上述问题,本文利用GSA 方法中莫里斯(Morris)筛选方法的首要影响(Elementary Effects,EE)与基于方差(Variance-based,VA)理论,全面定量分析参数对车辆系统响应状态的影响,对应的整体流程如图2所示。
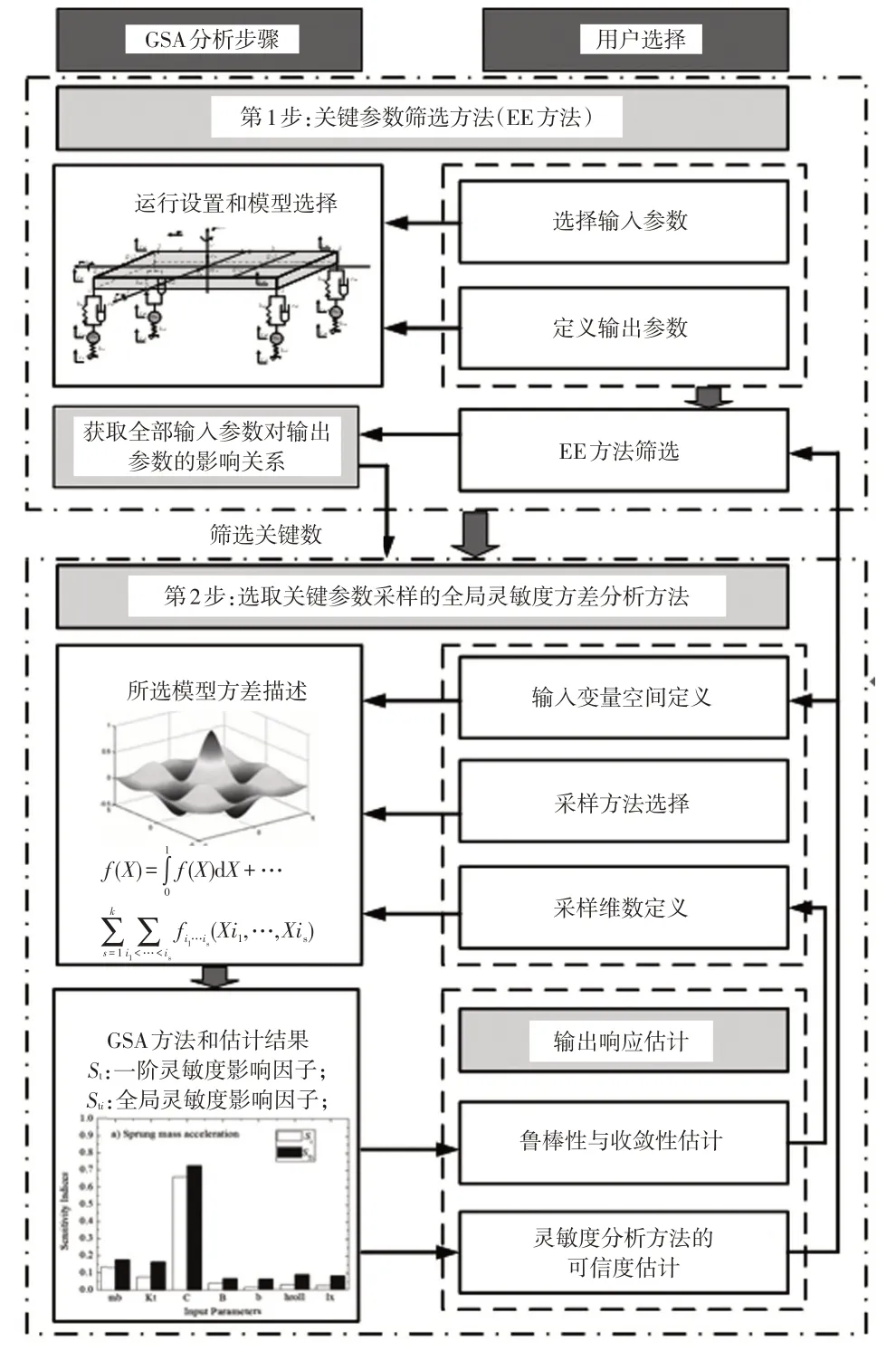
图2 双层GSA方法整体分析流程
3.1 Morris参数筛选方法
假设已知系统模型具有n个独立输入xi(i=1,2,…,n),此系统输入在n维空间中决定着p个系统输出,对于已知的系统输出参数X,利用EE方法可得第i个输入元素对已知系统模型的影响Eii:

式中,Δ为预定义数值且取值范围为{1/(p-1),2/(p-2),…,(i-1)/(p-i)};由于X=(x1,…,xi-1,xi,…,xn)是输入参数空间的随机采样,同理传递点(x1,…,xi-1,xi+Δ,…,xn)也是输入参数空间。
此处,EE方法提供2种测量敏感性数据分析方式:估计输入参数对于系统输出的整体均值μ;估计输入参数之间非线性与相互作用的最高阶方差σ。为了准确估计μ与σ,此处对不同输入参数x进行参数区域X中的随机采样,以保证采样区域的完整性。其中,μ代表EE方法的分布均值,其数值与相关度成正比;σ代表输入参数的非线性对输出响应的影响,其数值与非线性成正比。考虑到部分函数是非单调函数,其求解的μ存在正负相消的情况,为了改进此工况,本文采用改进的μ*(|Eii|)描述以上问题:

利用上述理论,参考CarSim 动力学软件提供的不同等级乘用车参数,对车辆悬架系统关键参数进行整理,如表1所示。
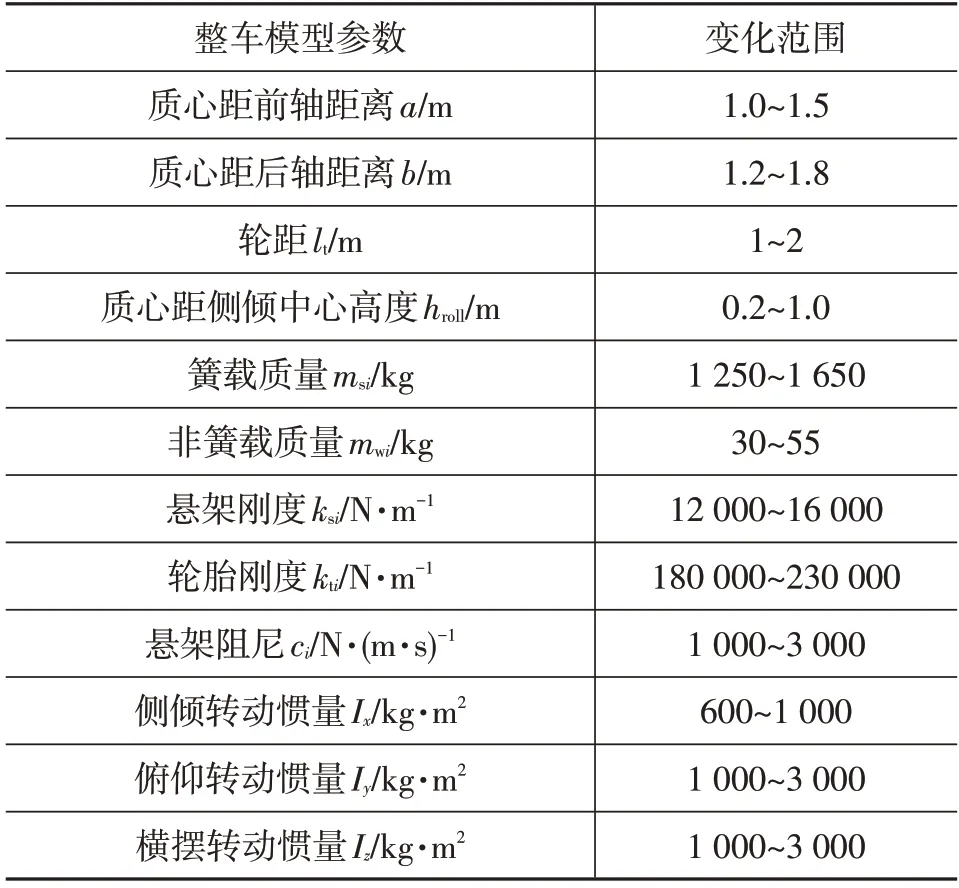
表1 整车系统参数选取范围
3.2 Morris筛选方法验证
利用CarSim 动力学软件中所提供的B 级车型(Hatchback),在80 km/h 车速、不同转向盘转角且不同路面激励工况下进行车辆系统输出参数对其垂向与横向响应影响的灵敏度分析验证,分别可得到不同转向盘转角以及ISO-A/C 级路面激励工况下,Hatchback 车型对应的系统输入参数与系统响应之间的灵敏度对应关系,如图3所示。

图3 不同工况下B级车型参数对系统垂向与横向响应灵敏度
由图3a、图3b 可知,转向盘大转角正弦输入ISOA/C 级路面激励工况下:车辆悬架系统的垂向响应(车辆簧载加速度、左前动行程与轮胎变形)主要受悬架阻尼、簧载质量、非簧载质量、轮胎刚度以及悬架刚度影响;横向响应(横向加速度与横摆角速度)主要受到簧载质量、质心与车辆前、后轴之间的距离以及悬架阻尼的影响,且影响趋势依次递减;侧倾响应(侧倾角与侧倾角速度)主要受到质心与侧倾中心间的侧倾高度、悬架阻尼、轮距、簧载质量以及侧倾转动惯量的影响。ISO-C级路面激励工况与ISO-A级路面激励工况相比,影响车辆垂向响应、横向响应以及侧倾响应的主要系统参数及影响程度类似。由此可知,Hatchback 车型在转向盘大转角输入且不同路面激励工况下,系统响应与系统输入参数之间灵敏度权重关系相对固定。
由图3c、图3d 可知,转向盘小转角输入工况下,Hatchback 车型在ISO-A/C 级路面激励工况下,车辆悬架系统的垂向响应也主要受悬架阻尼、簧载质量、非簧载质量、轮胎刚度以及悬架刚度影响,且对应参数影响权重也相近。由此可知,B级车型(Hatchback)在转向盘小转角不同路面激励工况下,路面因素对车辆系统响应影响较弱,且车辆垂向与横向响应主要受簧载质量影响。由于在此激励工况下,悬架阻尼与轮胎刚度主要影响车辆垂向响应,但对横向响应影响较弱;质心与车辆前、后车轴距离主要影响车辆横向响应,但对垂向响应影响较弱;车辆侧倾响应主要受簧载质量质心位置、悬架阻尼、轮距、簧载质量以及侧倾转动惯量影响,其他整车参数影响相对较弱。
4 系统全局灵敏度方差分析
4.1 Sobol敏感测试方法
基于协方差分析理论,Sobol 方法可以有效计算输入参数及其之间的耦合关系对系统输出的灵敏度[11]。首先,利用协方差方法计算系统分解方差V(i1…iX):
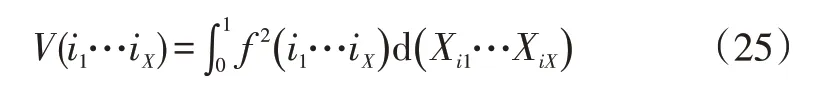
且全局方差V为:
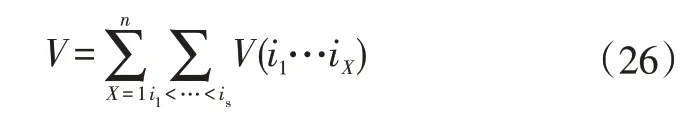
同时,全局灵敏度索引方差因子S(i1…iX)可表示为[12]:
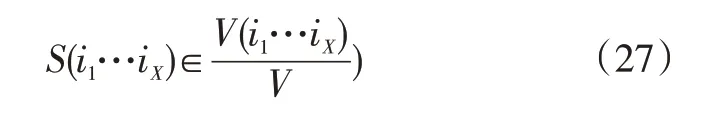
利用式(27)可知全局灵敏度索引因子为非负值,且:

其中,S(i1…iX)代表一系列变量i1,…,ix的灵敏度测量,与全局方差一一对应,即S1主要受参数X1影响,S12主要受X1与X2参数相互关系因素影响。
4.2 蒙特卡罗方法
在应用Sobol方法进行全局灵敏度分析时,均需使用蒙特卡罗方法求解对应系统参数的方差。具体可表示:
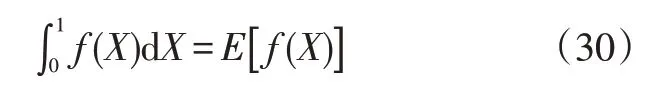
式中,E[f(X)]为数学期望,且近似为:
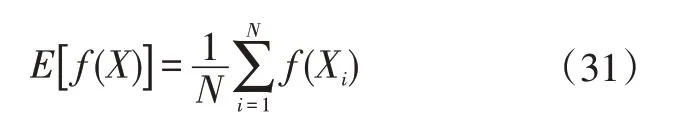
式中,{Xi}为空间In中长度为N的随机序列,且当N→∞时式(30)和式(31)近似相等,且对应参数之间相互关系如表2、表3所示。其中,Sα为所有参数方差S(i1…iX),为所有输入参数对系统输出的灵敏度索引因子,I为单位矩阵。

表2 α与β子集灵敏度索引因子关键参数总结

表3 基于全局灵敏度索引因子的输入参数相关性
首先,在空间In中选取2 个随机独立的一致点,即π1=[α1;β1]与π2=[α2;β2];利用模型f(X)对这2 个点进行估计,得到f(π1)与f(α1;β1)。假设模型f(X)平方可积,对于独立采样点N(N→∞),有:
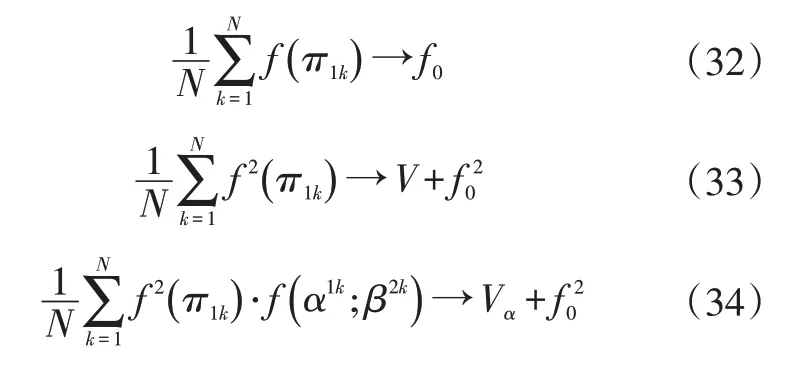
利用式(32)~式(34)可对一阶灵敏度索引因子Vα进行变换:

式(35)说明了V(i1…im)关于参数α在(m-r)维随机序列中的方差总和,且π1k为第k点的随机独立一致点。
同时,在置信度50%工况下的Vα估计关联误差可表示为:

采用以上方法可以有效避免蒙特卡罗方法在随机取点中的堆栈以及取空等问题,且为减少取样数量N,对于采样k插入2n维拟随机点,并将其平分为2 个n维的与,对其进行描述计算。
4.3 全局灵敏度方差分析方法仿真分析
利用以上理论,可得此工况下对应的簧载质量、轮胎刚度、悬架阻尼、轮距、质心与后轴的距离、侧倾中心与质心的距离以及侧倾转动惯量对应车辆垂向以及横向响应的一阶灵敏度影响因子,以及全局灵敏度影响因子,如图4所示。
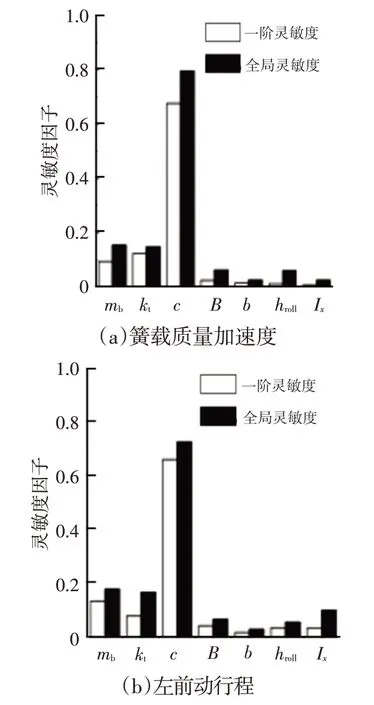


图4 转向盘小转角A级路面激励工况下B级车型关键系统参数对垂向与横向响应全局灵敏度影因子
由图4可知:此工况下车辆悬架垂向响应主要受悬架阻尼、轮胎刚度、簧载质量以及悬架刚度参数影响;横向响应主要受到簧载质量、质心与车辆前、后轴之间的距离的影响,且影响程度依次递减;侧倾响应主要受簧载质量质心位置、悬架阻尼、轮距、侧倾转动惯量以及簧载质量影响,且影响程度依次递减。
参考转向盘小转角A级路面激励工况,可得此工况下系统输出参数对应车辆垂向与横向响应的一阶灵敏度影响因子以及全局灵敏度影响因子,如图5所示。
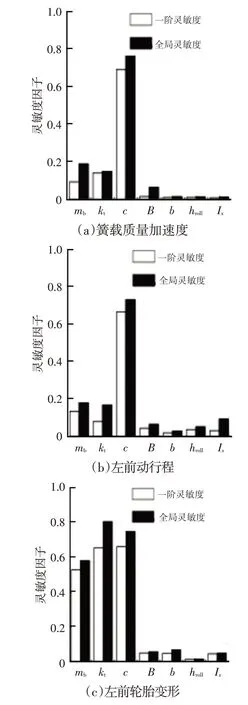

图5 转向盘大转角C级路面激励工况下B级车型关键系统参数对垂向与横向响应全局灵敏度影因子
由图5可知:此工况下车辆悬架垂向响应受悬架阻尼、簧载质量、胎刚度以及悬架刚度参数的影响明显;横向响应主要受到簧载质量、质心与车辆前、后轴之间的距离以及悬架阻尼影响;侧倾响应主要受到簧载质量质心位置、悬架阻尼、轮距、簧载质量以及侧倾转动惯量影响。以上分析可知,B级车型在转向盘大转角ISO-C级路面激励工况下,得出的结论与利用EE 方法在此工况下所获的结论相似,但是方差分析方法相较于后者,灵敏度权重系数存在一定差异。
5 整车系统台架试验
为进一步验证所设计双层GSA 方法的有效性,此处基于已搭建整车半主动悬架测控平台系统,以转向盘转角15°、车速40 km/h 的J-turn 实车行驶工况为例,对获取的侧倾角速度和横摆率试验数据,与整车观测器仿真数据进行比较[13-14],如图6所示。

图6 整车测试系统整体框架
利用上述测试平台,在上述仿真类似工况下,利用整车模型关键参数对系统响应状态估计结果进行验证。同时,为进一步说明利用所设计双层GSA 方法对实车系统响应结果与整车观测器得到的侧倾角速度与横摆率之间的差异,引入标准偏差对数据结果进行对比,如表4所示。
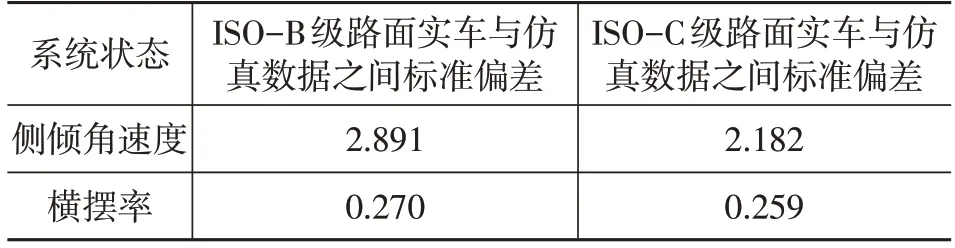
表4 实车数据与整车观测器仿真数据标准偏差对比
由表4可知,ISO-C级路面侧倾角速度标准偏差较ISOB级路面小。综合以上仿真与试验验证结果可知,所设计的双层GSA方法在整车状态识别影响方面有较好效果。
6 结束语
本文基于双层全局灵敏度分析方法对车辆悬架系统响应状态及其动态特性进行定量分析并试验验证,进而为基于关键参数的车辆系统底盘控制提供一定的理论与实践参考,主要得出以下结论:
a.所提出的双层GSA 方法采用的灵敏度指标对车辆速度和车辆类型具有较好鲁棒性。
b.ISO-B 级与ISO-C 级路面系统响应状态对应的标准偏差不高于3,验证了双层GSA方法的有效性。

