基于三维变分和神经网络算法的压水堆堆芯燃耗分布数据同化方法研究

郭 林，万承辉，李云召，吴宏春

(西安交通大学 核科学与技术学院，陕西 西安 710049)

压水堆中堆芯的燃耗分布对于反应堆的燃料管理[1]、组件性能评价、乏燃料处理等具有重要意义。而在反应堆运行期间，无法通过实验方法直接测量得到燃耗分布，数值模拟一直是确定堆芯燃耗分布最重要的方法。数值模拟方法需根据堆芯设计方案建立对应的物理模型，但由于堆内构件制造偏差、堆芯流量分配不均等因素，数值模拟与真实堆芯之间不可避免地存在一定偏差，直观上表现为功率分布的计算值与实测值之间存在一定差异。而堆芯燃耗分布是功率分布对时间的积分，功率分布的计算误差是导致堆芯燃耗分布的计算误差最主要的原因之一。因此，如何提高堆芯燃耗分布的计算精度，是压水堆数值模拟中需要解决的关键问题。

在工程科学中，数据同化方法可将不同物理场空间的实测数据和数值模拟结果有机地结合，实现对工程参数更高精度预测的目标。数据同化技术目前已在数值天气预报[2]、陆面过程模型[3]等方面得到了广泛应用和验证。近年来随着数据同化方法的发展，将其应用于反应堆领域的研究也日益增多：Clerc等[4]采用三维变分(3DVAR)算法，通过功率分布实现了二维径向反射层组件参数的优化计算；刘蕴等[5]采用改进的变分数据同化实现了更准确的核事故源项反演；Bouriquet等[6-7]采用3DVAR，研究了PWR900堆芯中不同测量装置对于物理场重构的影响；另外，Bouriquet等[8]采用不同的数据同化方法对PWR900测量装置的布置进行了优化；Ponçot等[9]比较了不同变分同化方法对于堆芯氙动态预测的效率；Wan等[10]应用线性最小二乘方法对核数据进行调整，实验模拟有效增殖因数keff的误差降到25 pcm以内，同时将keff的相对不确定度从1%降到0.15%左右。目前数据同化方法在核反应堆领域的研究大多针对测量装置优化、功率重构、核数据调整等，尚未有应用于堆芯燃耗分布的研究。

本文基于3DVAR算法和神经网络算法，研究适用于压水堆堆芯燃耗分布的数据同化方法，旨在利用堆芯功率分布的实测值校准堆芯燃耗分布的计算值，从而在一定程度上降低其与真实值之间的误差。基于本文提出的堆芯燃耗分布数据同化方法，在我国某商用压水堆核电厂上已完成对该同化方法的验证。

1 理论模型

本文利用堆芯功率分布的实测值建立了针对堆芯燃耗分布的同化模型，对燃耗分布进行高精度的反演校准，降低数值模拟与工程实践之间的误差，实现堆芯燃耗分布更高精度的计算。下面分别详细介绍三维变分算法和神经网络算法的理论方法。

1.1 三维变分算法

3DVAR通过构建代价函数描述燃耗分布的计算值和真实值之间的差异，利用变分思想把数据同化问题转化为代价函数极值求解问题，其代价函数表达式为：

(1)

式中：x为堆芯燃耗分布的同化值；xb为堆芯燃耗分布的计算值；yo为堆芯功率分布的实测值；H为观测算子，表示堆芯燃耗分布与功率分布之间的函数关系；B为堆芯燃耗分布误差协方差矩阵；R为功率分布误差协方差矩阵。

对于矩阵B，由于燃耗分布的真实值无法测量得到，因此本文采用应用广泛的二阶自回归模型[11](SOAR)来近似估计矩阵B，其主要公式如下：

B=B0C

(2)

(3)

式中：B0为待定标量系数；rij为两组件的径向距离；L为特征长度，取1个组件的径向宽度。

对于矩阵R，假设组件相对功率之间无相关性，则R可近似为对角阵。本文采用目标堆芯的功率分布的误差限值要求作为其不确定度，即：相对功率大于0.9的组件，其相对误差不超过5%；小于0.9的组件，其相对误差不超过8%。因此，矩阵R可表示为：

(4)

对于观测算子H，由于压水堆是一个核-热-燃耗多物理场紧密耦合的系统，无法显式地给出堆芯燃耗分布和功率分布之间的函数关系。因此，本文采用神经网络算法，通过对大量堆芯功率分布和燃耗分布样本的机器学习，获得所需的观测算子H。

1.2 神经网络算法

神经网络算法是一种在输入参数和输出参数建立连接关系的强大工具。神经网络的设计构造最早收到生物神经网络连接的启发，由最初的多层感知机不断发展，到现在的全连接神经网络、卷积神经网络、循环神经网络、生成对抗网络等多种结构[12]，并在深度学习等领域广泛应用。本文采用全连接神经网络[13]获得H的显式表达式，该网络通常由3部分构成，即输入层、隐藏层以及输出层，其结构如图1所示。图中非“+1”的圆圈表示神经元，“+1”圆圈与神经元连接线表示偏置。

图1 全连接神经网络结构Fig.1 Structure of fully-connected neutral network

对于输入层和输出层有：

a(1)=W(1)x+b(1)

(5)

y=W(out)z(p)+b(p)

(6)

式中：a(1)为第1隐藏层收到的信号向量；W(1)为输入层与第1隐藏层之间的权重矩阵；b(1)为第1隐藏层的偏置向量；W(out)为输出层与第p隐藏层之间的权重矩阵；b(p)为第p隐藏层的偏置向量；z(p)为第p隐藏层神经元的输出信号向量；x和y分别为输入向量和输出向量。

对于中间隐藏层有：

a(g)=W(g)z(g-1)+b(g)

(7)

z(g)=f(a(g))

(8)

式中：a(g)为第g隐藏层收到的信号向量；W(g)为第g-1隐藏层与第g隐藏层之间的权重矩阵；b(g)为第g隐藏层的偏置向量；f为激活函数；z(g)为第g隐藏层的输出信号向量。

2 数值验证

2.1 神经网络训练结果及分析

为建立堆芯燃耗分布与功率分布之间的神经网络模型，本文采用Bamboo-C软件系统[14]对某压水堆堆芯建模模拟并得到燃耗分布。在不同燃耗分布下，采用随机抽样方法产生10 000个堆芯燃耗分布的样本，并采用Bamboo-C计算得到对应的功率分布样本。将燃耗分布样本和对应的功率分布样本组成数据集，并按照8∶1∶1的比例分割成3个子数据集：训练集、验证集和测试集。基于训练子数据集，通过TensorFlow[15]框架搭建全连接神经网络结构进行训练，损失函数采用训练输出的功率分布与给定样本之间的均方误差；基于验证集和测试集检验训练模型。

训练集和验证集预测功率的相对误差最大值随训练轮数的变化如图2所示，训练过程训练集和验证集功率分布相对误差的最大值随训练轮数增加逐渐减小。训练完成后最大相对误差及测试集的测试结果列于表1，不同数据集中预测功率相对误差的最大值为5.19 GW·d/tU下训练集的1.11%。由此表明本文构建的神经网络模型在给定堆芯燃耗分布的条件下，对堆芯功率分布的预测具有满足要求的精度和可靠度。因此，基于本文建立的堆芯燃耗分布与功率分布之间的神经网络模型，可以较高精度地获得观测算子H的显示表达。

图2 最大相对误差变化Fig.2 Change of maximum value for relative error

表1 不同子数据集的最大相对误差Table 1 Maximum value of relative errors in different sub-datasets

2.2 燃耗分布同化结果及分析

由神经网络模型确定观测算子H后，求解代价函数极值即可获得同化后的燃耗分布。近年来深度学习领域中的Adam优化方法[16]得到了广泛应用，具有高效、占用内存少、大规模参数优化适用性等特点，因此本文采用该方法进行燃耗分布多极值优化问题的求解。由于矩阵B对函数求解有着直接的影响，因此本文首先对B开展了敏感性分析。以第1个燃耗点2.79 GW·d/tU为例，分别选取B0=10n，n=-1，0，1，2，3等5种不同取值进行分析[17]，结果表明，当B0=1时，SOAR方法具有较好的效果，因此B0取为1。此时，同化后的功率分布相对误差最大为3.96%，最小为-1.96%，相较于同化前功率分布的相对误差最大值5.35%和最小值-2.46%，具有明显的改善效果。同化后的组件燃耗分布相较于同化前的绝对偏差如图3所示，同化后的燃耗分布相较于同化前最大绝对偏差为0.46 GW·d/tU，最小为-0.47 GW·d/tU，偏差RMS为0.23 GW·d/tU，此时的燃耗调整量相对于堆芯平均燃耗深度2.79 GW·d/tU较为合理。在其他燃耗点下，按照上述步骤进行B0的敏感性分析，选取SOAR效果最好的B0进行3DVAR。并在每一步完成燃耗分布数据同化后选用同化后的燃耗分布进行CNP1000功率历史模拟。为进一步验证燃耗分布同化的正确性，本文将结合数据同化的功率历史模拟与初始不结合数据同化的功率历史模拟进行对比分析，分析参数包括功率分布、临界硼浓度(CBC)、轴向功率偏移(AO)、热点因子(Fq)和焓升因子(FΔH)等。

图3 2.79 GW·d/tU同化前后的燃耗分布偏差Fig.3 Bias of burnup distribution before and after assimilation at 2.79 GW·d/tU

功率分布相对误差对比如表2所列，结合数据同化的功率历史模拟在每个燃耗步都降低了功率分布的相对误差，降低后的相对误差均满足压水堆的限值要求。其中最大改善效果为10.04 GW·d/tU下，功率分布最大相对误差由9.53%降到5.11%。CBC、AO、Fq和FΔH误差对比分别如图4所示，由于本文研究针对于径向二维燃耗分布，且同化前后的堆芯平均燃耗深度保持一致，结合数据同化的功率历史模拟基本不改变CBC误差和AO误差，其中CBC平均误差由-19.0 ppm变为-19.8 ppm，AO平均误差由-0.58%降到-0.56%；Fq和FΔH误差略有减小，且随着燃耗加深改善程度逐渐变小，其中Fq平均误差由-0.054降到-0.048，FΔH平均误差由-0.029降到-0.021。

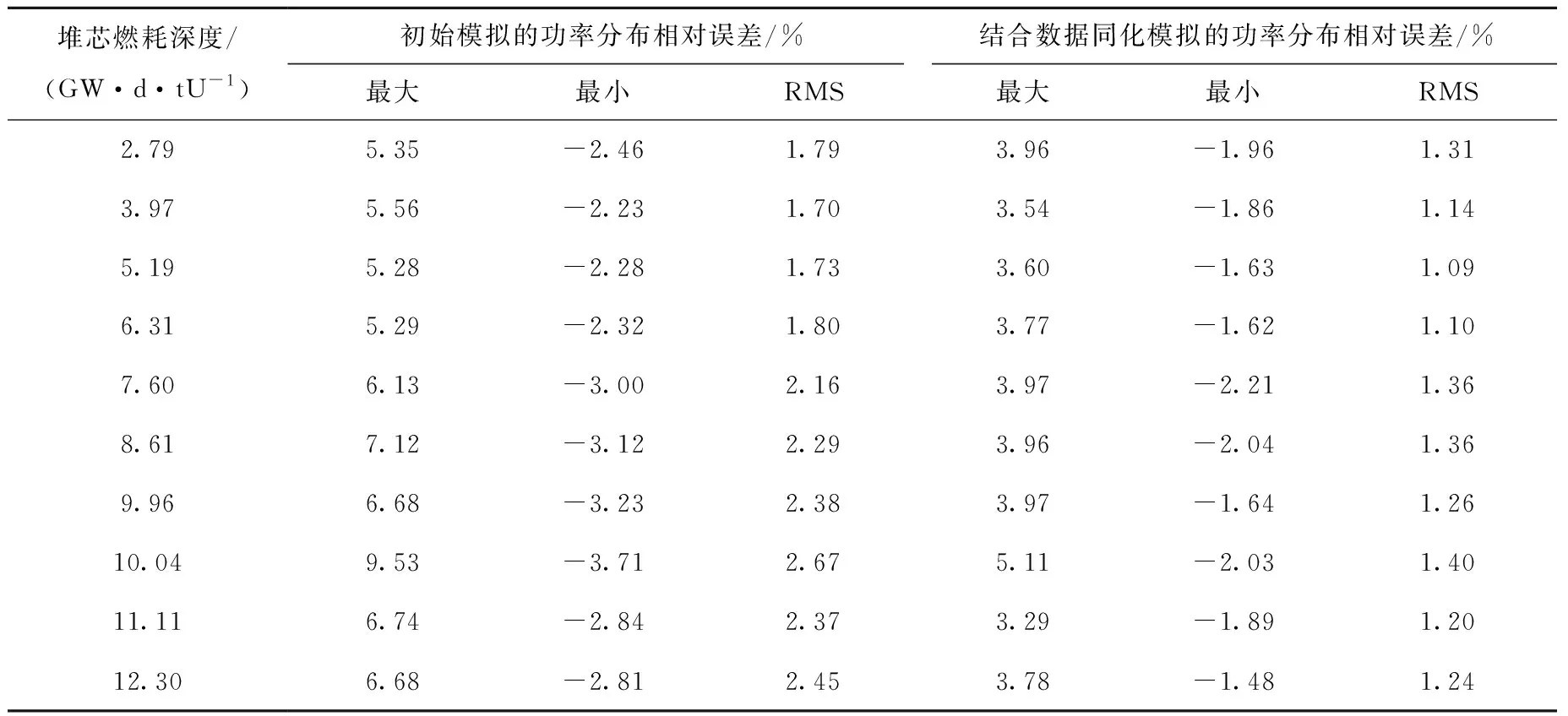
表2 功率分布相对误差对比Table 2 Comparison of relative errors for power distribution

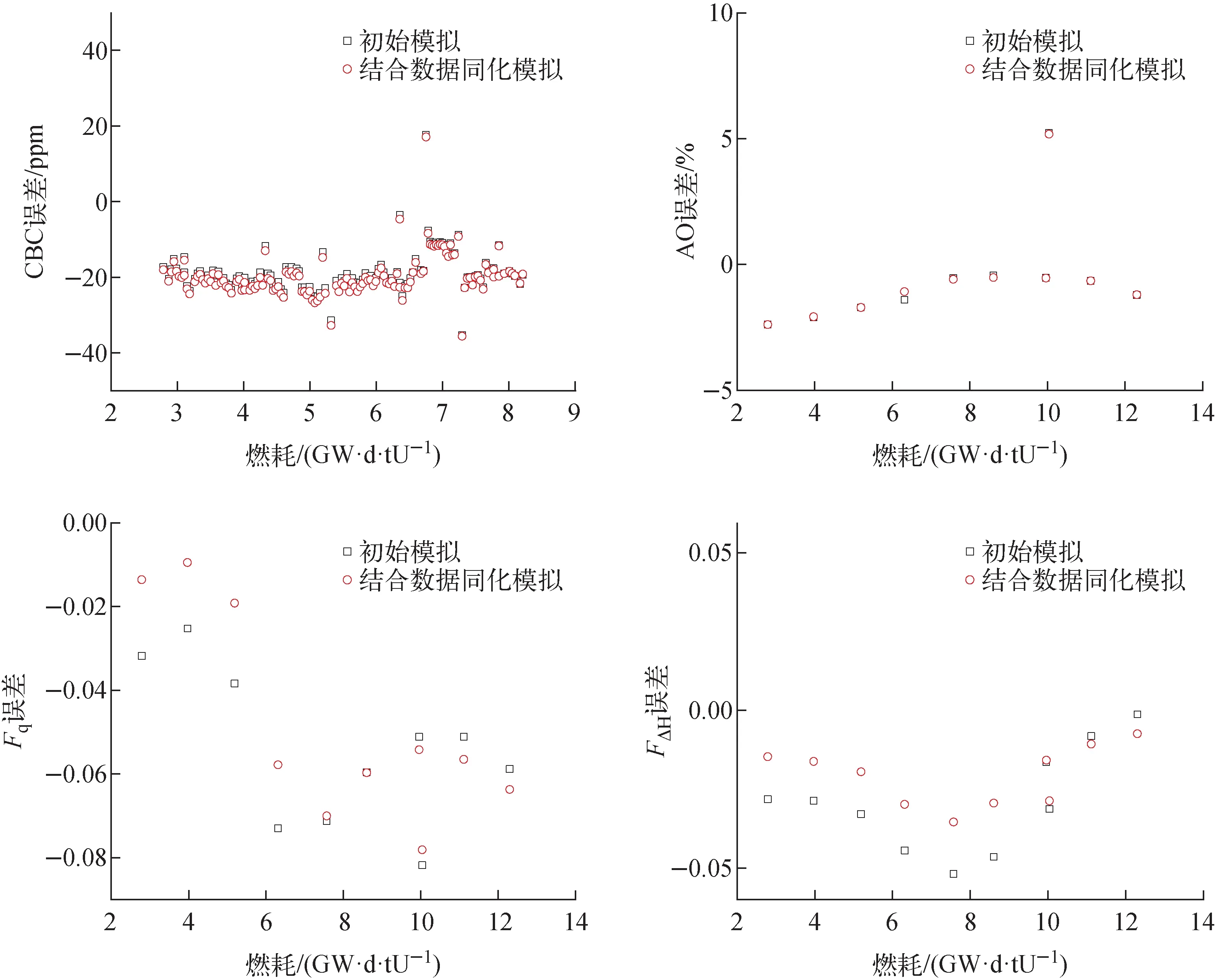
图4 其他重要参数误差对比Fig.4 Comparison of other important parameters’ errors

结合上述数值结果可知，燃耗分布数据同化对于功率分布具有一定的改善效果，但功率分布误差来源有多种因素，因此本文只针对于燃耗分布的数据同化无法使功率分布误差进一步下降，针对燃耗的同化对于功率分布的改善效果有限，需增加对其他参数的联合同化，彻底解决功率计算误差的原因。

3 结论

本文基于三维变分算法和神经网络算法，有机地结合堆芯燃耗分布与功率分布，开展了压水堆堆芯燃耗分布同化方法研究，利用堆芯功率分布的实测值建立了燃耗分布的数据同化模型。数值结果表明，燃耗分布同化对功率分布的改善效果较为明显；由于同化前后堆芯平均燃耗深度不变，其对CBC和AO基本无影响，对FΔH、Fq的改善效果较小。因此，本文提出的基于三维变分和神经网络算法的压水堆堆芯燃耗分布同化方法可有效地达到提高压水堆堆芯燃耗分布计算精度的目标，从而进一步提升反应堆运行的安全性和经济性。作为下一步的研究计划，拟将基于本文提出的同化方法，开展结合其他重要参数的联合数据同化方法研究。