方波驱动下双气泡的动力学行为*
王寻 黎奥 周敏 梁金福 张泽坤 吴伟
(1 上海电机学院凯撒斯劳滕智能制造学院上海 201306)
(2 中国科学院声学研究所语言声学与内容理解重点实验室北京 100190)
(3 西安工程大学理学院西安 710048)
(4 贵州师范大学物理与电子科学学院贵阳 550025)
0 引言
超声在液体中传播时,会使得液体分子疏密程度发生变化。当声压达到一定程度后,液体中气核将成长为肉眼可见的气泡,这种现象被称为声空化[1]。声空化在乳化[2]、清洗[3]和催化[4]等领域都有广阔的应用前景。在实际应用时通常存在大量空化泡组成的空化泡群,双气泡动力学的相关研究有利于人们深入理解气泡群中气泡的相互作用[5]。因此,近年来双气泡动力学问题逐渐成为研究热点。Ida[6]采用非线性双气泡模型研究气泡的相互作用,发现气泡辐射的声波包含了正向和负向脉冲。一个气泡的负向脉冲是由另一个气泡收缩时产生的正向脉冲引起的。卢义刚等[7]通过数值计算研究了气泡间距以及驱动超声幅值和频率对双泡动力学的影响,并对比了双频与单频驱动下气泡半径的变化规律。张鹏利等[8]通过数值计算研究了单频声波驱动下初始半径、驱动声压幅值和频率以及液体黏滞系数对双空化泡膨胀比和溃灭时间的影响,研究表明增大一个空化泡的平衡半径会抑制另一个空化泡的膨胀。王德鑫等[9]研究了双气泡内部气体为3种不同的惰性气体情况下气泡的脉动,探讨了惰性气体类型对气泡回弹阶段动力学行为的影响。李想等[10]推导出双气泡系统中气泡的共振频率,并研究了驱动声波频率、气泡间距和声波在驱动双气泡时的相位差对气泡动力学的影响。研究表明当气泡半径在线性变化的范围内时,单个气泡的动力学频谱数据包含了双气泡系统所有的频谱信息。若出现非线性变化,则上述结论不成立。此外,该研究证实了气泡间距对次Bjerknes力有非常显著的影响。Zhang等[11]研究了双频声波驱动下两个气泡间的次Bjerknes力,探讨了多个参数对次Bjerknes力的影响。
本课题组此前的研究探讨了超声驱动下气泡的非球形振动[12]以及气泡相位对气泡间次Bjerknes力的影响[13]。在这些报道中,驱动声波均为正弦波。然而根据Sun等[14]的研究,方波可以使得气泡在收缩时产生更高的温度,可能有利于化学反应的进行。王捷[15]的研究也表明,在驱动声波幅度相同的情况下,方波能够提供更大的功率,这使得气泡能够生长到更大的尺寸并发生更加剧烈的崩溃,其空化强度明显较大,这对提高声化学效应有很大的帮助。但文献[15]仅研究了单个气泡的情况,在实际应用时,存在气泡间的相互影响。本文将对方波驱动下的双气泡脉动进行研究,探讨气泡平衡半径和驱动声压幅值对双气泡组成的系统动力学行为的影响,为后续的实验研究和实际应用打下基础。
1 双气泡动力学方程
对于双气泡系统,可使用Keller-Miskis方程描述气泡的径向振动[9]:
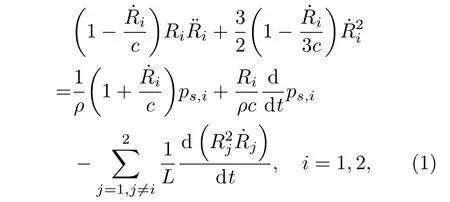
其中,Ri为气泡半径,c和ρ为液体中声速和密度,L为两个气泡的间距,i为气泡序号。ps,i可以表示为

其中,P0为环境压强,μ和σ分别为液体的黏滞系数和表面张力系数,Pd为驱动声压。本文设定驱动声波为方波,Pd可以表示为[14]

其中,Pus为声波幅度,f为方波变化频率,n越大则驱动声波越接近标准方波。本文中设置n=109。在公式(2)中,Pg,i为第i个气泡内部的压强,满足[16]

其中,Ri0为第i个气泡的平衡半径,γ为气泡内气体的多方指数,bi为第i个气泡的范德瓦尔斯半径。对于空气,bi=Ri0/8.5。与气泡中心距离为x处的辐射声压为[17]
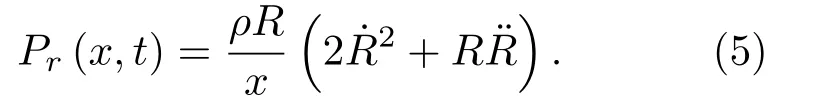
在本文中与参考文献[17]一致,设置x=10-3m。气泡间的次Bjerknes力为[18]

其中,V1和V2为两个气泡的体积,er为径向单位矢量,FB为正值时两气泡相互排斥,FB为负值时两气泡相互吸引。气泡收缩时能够达到的最高温度和最大压强分别为[19]
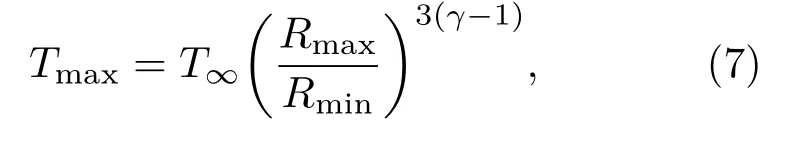

其中,T∞为液体温度,Pv为饱和蒸汽压,Rmax和Rmin为气泡收缩前的最大半径和收缩后达到的最小半径。
2 数值计算与分析
2.1 与正弦波驱动下的气泡脉动对比
采用四阶Runge-Kutta方程数值求解等式(1)~(4),即可得到两个气泡在脉动时半径的演化,进而求出次Bjerknes力。求解时使用的参数如下:ρ=998.2 kg/m3,c=1481 m/s,P0=1.013×105Pa,γ=1.4,η=1.0×10-3Pa·s,σ=7.275×10-2N/m,f=2.0×104Hz,R10=5 μm,R20=2 μm,L=300 μm,Pus=1.3×105Pa。数值计算结果如图1和图2所示。为了对比,在图1和图2中也画出了相同幅度的正弦波驱动下气泡半径及气泡间次Bjerknes力的变化曲线。需要说明的是,公式(6)中计算FB时用的是时间平均值。本文与文献[11]和文献[20]一致,计算瞬时FB值。如果需要研究某一段时间范围内的平均次Bjerknes力,则对瞬时FB积分再求平均即可。
对比方波驱动和正弦波驱动下的气泡半径变化曲线(图1)可以看出,当驱动声波幅度相同时,方波驱动下两个气泡最大半径相对较大。这是因为在气泡膨胀阶段,方波能提供更大的负声压,使得气泡半径快速增大。这与文献[21]中对单气泡动力学的研究结果是一致的。在图2中,方波驱动下气泡间次Bjerknes力幅度相对较大,且主要为负值,即两气泡相互吸引(图2(a));正弦波驱动下次Bjerknes力幅度相对较小,在正负值之间交替变化(图2(b))。
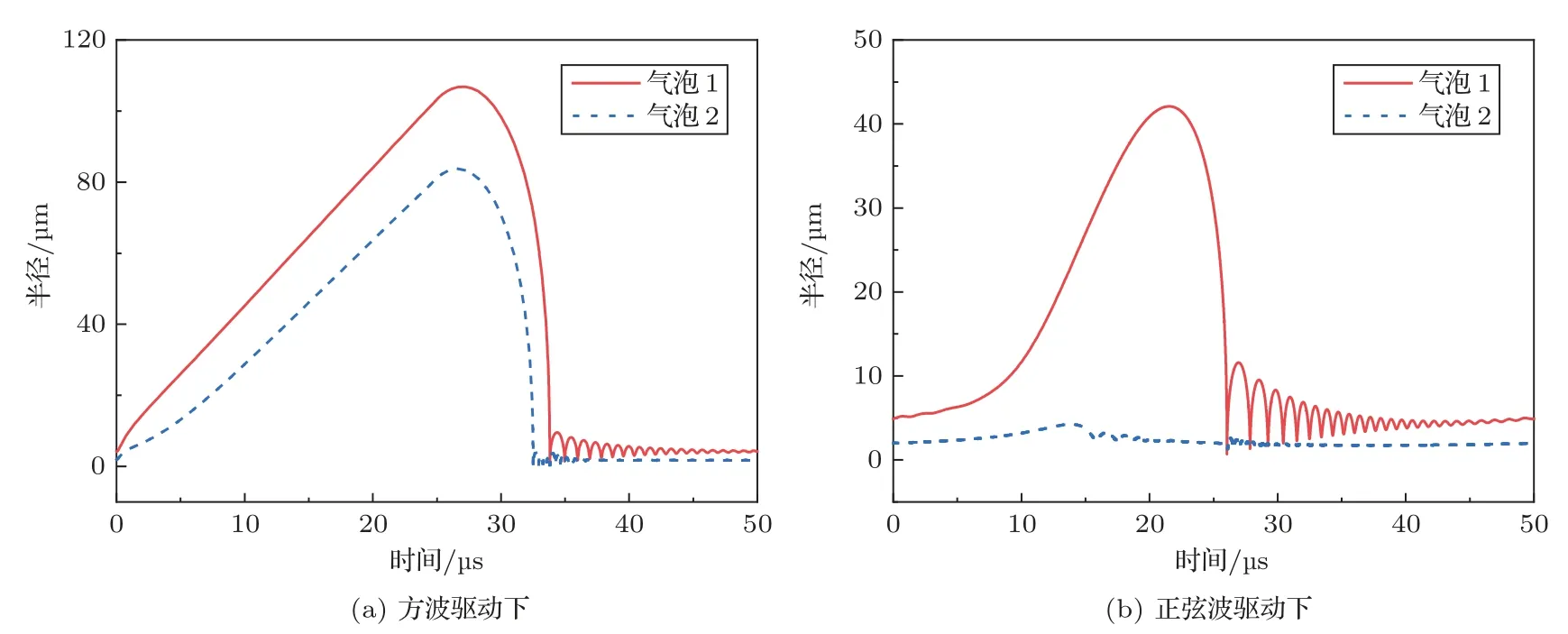
图1 方波和正弦波驱动下气泡的半径变化Fig.1 Radii of bubbles under the driving of square wave and sine wave

图2 方波和正弦波驱动下气泡半径及气泡间次Bjerknes力的变化Fig.2 Secondary Bjerknes force of bubbles under square wave driving and sine wave driving
气泡的声化学效应和气泡收缩时的温度和压强有很大的关系,高温和高压的环境更有利于声化学反应的进行[22]。在求得不同时刻的气泡半径后,可根据公式(7)和公式(8)计算气泡收缩时的最大温度Tmax和最大压强pmax。计算时依据文献[23],设置公式(8)中Pv=2338 Pa。设置驱动声压幅度Pus在0.2×105~1.0×105Pa之间变化,求出方波和正弦波驱动下两气泡的Tmax和pmax,如图3所示。在驱动声压幅值(Pus)较低时,与正弦波驱动的情形相比,方波驱动为Tmax和pmax带来的提升效果不明显。但随着Pus的增大,两种波形驱动下两气泡的Tmax和pmax的差异越来越大。这表明当驱动声压较高时,方波对声化学反应的提升效果更为明显。需要指出的是,文献[19]计算Tmax和pmax时采用的是绝热模型,没有考虑到传热引起的气泡内部温度降低,所以计算得到的Tmax和pmax会比真实值高。然而在一定程度上仍足以说明使用方波比使用正弦波更有利于声化学反应的进行。

图3 不同幅度声压驱动下两气泡内部最高温度和最大压强Fig.3 Maximum pressure and temperature in bubbles with different driving amplitudes
2.2 驱动频率对气泡动力学的影响
保持其他参数不变,将公式(3)中驱动频率f依次设置为25 kHz、30 kHz和35 kHz,进行数值计算,得到的双气泡半径和气泡间次Bjerknes力的变化曲线如图4和图5所示。由图4可以看出,随着驱动频率的增加,气泡能够达到的最大半径逐渐减小。这是由于频率升高使得每个声周期中负压时间缩短,气泡膨胀时间变短,气泡来不及生长到更大的尺寸。另外,频率的增加也会使得气泡体积变化速率变小,气泡间次Bjerknes力的幅度也会减小(图5)。
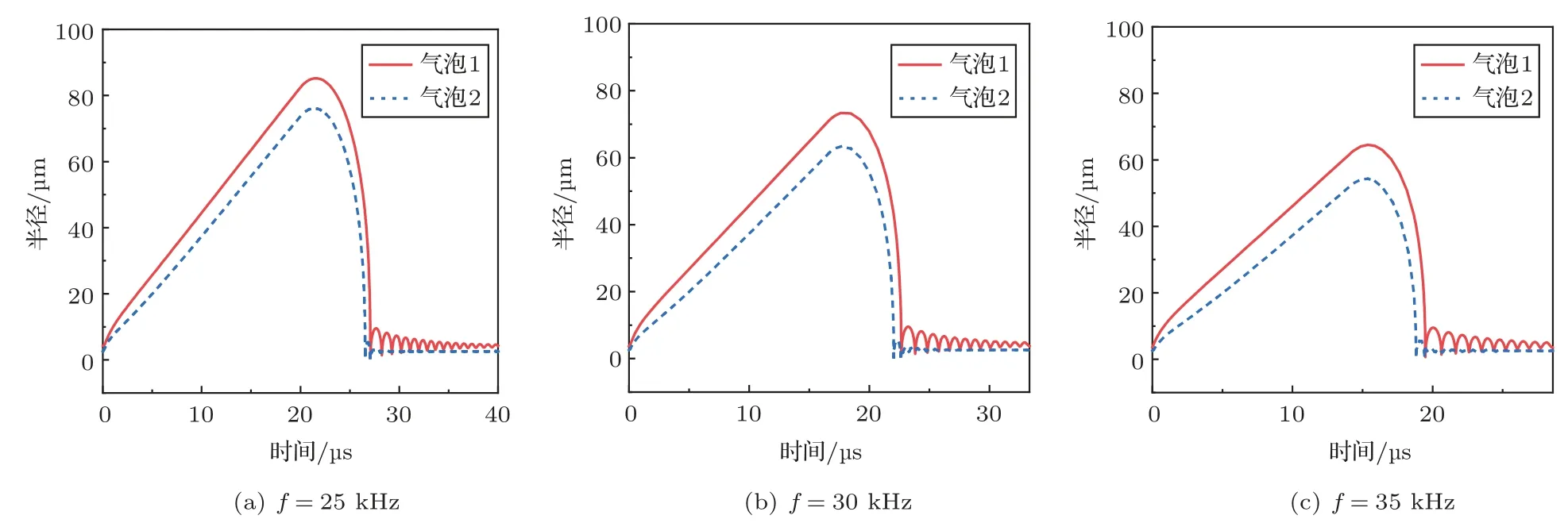
图4 不同驱动频率时气泡的半径变化Fig.4 Bubble radii under different driving frequencies

图5 不同驱动频率时气泡间次Bjerknes力Fig.5 Secondary Bjerknes force between bubbles under different driving frequencies
2.3 平衡半径对气泡动力学的影响
固定R10=5.0 μm,依次R20设置为3.5 μm、3.0 μm和2.5 μm,进行数值计算。得到的双气泡在崩溃时刻的辐射声压如图6(a)所示。其中实线和虚线分别表示气泡1和气泡2的辐射声压。可以看出,随着R20的减小,气泡1和气泡2的崩溃时刻均会提前,但由于气泡2崩溃提前的时间量大于气泡1,两个气泡崩溃时刻的时间间隔将会增加。另外,随着R20的减小,两个气泡的辐射声压幅度也会增加。这表明增大双气泡平衡半径的差异能够增强气泡崩溃的剧烈程度。图6(b)为一个脉动周期中气泡间次Bjerknes力随时间的变化。由图6(b)可以看出,随着R20的减小,气泡间次Bjerknes力也会减小,气泡间相互吸引力减弱。

图6 气泡2的平衡半径为不同值时气泡的辐射声压和次Bjerknes力Fig.6 Radiation pressure and secondary Bjerknes force when the equilibrium radius of bubble 2 takes different values
2.4 驱动声压幅度对气泡动力学的影响
驱动声压幅值也对双气泡动力学行为有很大的影响。设置R10=5.0 μm,R20=3.5 μm,令公式(3)中Pus分别为1.00×105Pa、1.05×105Pa、1.10×105Pa和1.15×105Pa,数值计算后得到双气泡半径随时间变化曲线如图7所示。图8展示了上述驱动声压下的气泡的辐射声波。在图7和图8中,当t∈[0,25 μs)时,方波声压为负值,当t∈[25 μs,50 μs]时,方波声压为正值。可以看出,随着驱动声压的增大,两个气泡在膨胀时能达到的最大半径都有所增加。这意味着使用大幅度方波驱动可以增大两个气泡崩溃的剧烈程度。从图7(a)~图7(d),负声压阶段气泡的振荡次数逐步减少。在图7(a)和图7(b)中,两个气泡几乎同时崩溃。但在图7(c)中,气泡1的崩溃明显发生了延迟,此时气泡2比气泡1更早崩溃。在图7(d)中,气泡1的崩溃被进一步延迟,而气泡2的崩溃也有所延迟,两个气泡崩溃的时间差有所减小。
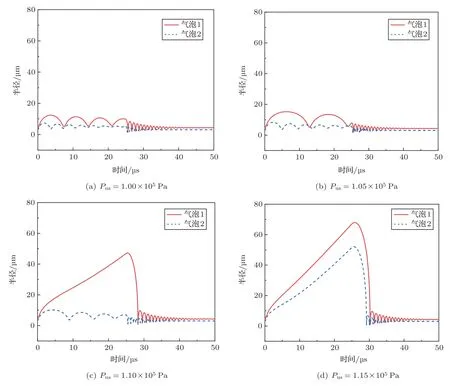
图7 不同幅度的声波驱动下气泡的半径Fig.7 Radii of bubbles under driving of different amplitudes
在图8(a)和图8(b)中,由于两个气泡的脉动均相对较弱,在正声压相回弹后的振荡中的每一次收缩都会辐射一个小幅度的脉冲波,且气泡1辐射声波的声压幅度大于气泡2。对比图8(a)和图8(b),可以看出增大驱动声波幅度会减弱气泡1振荡阶段的辐射声波,增强气泡2振荡阶段的辐射声波。在图8(c)中只能明显看到气泡1的辐射声波,这是因为当Pus=1.10×105Pa时,气泡1的崩溃比气泡2剧烈很多,此时气泡1辐射的声压幅值远大于气泡2。在图8(d)中,气泡1和气泡2均发生快速收缩,在崩溃时均出现了显著的辐射声波,而振荡阶段的脉冲波则很难观察到。
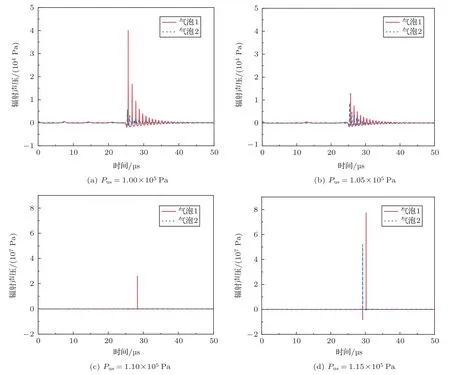
图8 不同幅度的声波驱动下气泡的辐射声压Fig.8 Radiation pressures of bubbles under driving of different amplitudes
图9(a)和图9(b)展示了驱动声压幅度为1.00×105Pa和1.15×105Pa时气泡间次Bjerknes力。当驱动声压幅度为1.00×105Pa时,次Bjerknes力主要出现在正压相时气泡的振荡阶段。当驱动声压幅度为1.15×105Pa时,次Bjerknes力主要出现在气泡的快速收缩阶段。后者的量级约为前者的104倍。
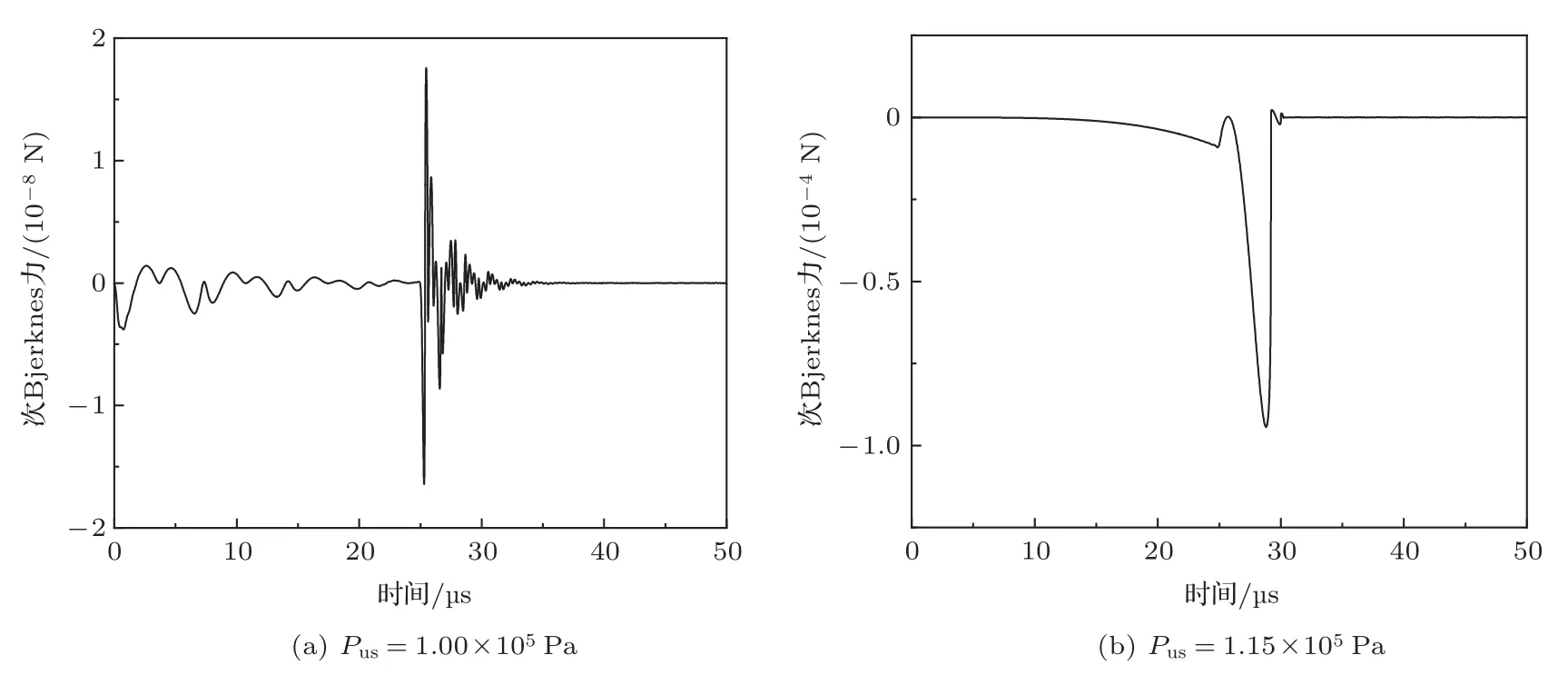
图9 不同幅度的声波驱动下气泡间次Bjerknes力Fig.9 Secondary Bjerknes force between bubbles under driving of different amplitudes
3 结论
本文通过数值计算对方波驱动下的双气泡动力学问题进行了研究。研究发现,随着驱动声波频率的提高,两个气泡能达到的最大半径减小,气泡间次Bjerknes力也会减小。增大双气泡平衡半径的差距,会使得两个气泡崩溃时刻的时间间隔变长,收缩时辐射声压幅度增大,次Bjerknes力幅度减小。此外,本文也详细讨论了在逐步提高驱动声压幅值的过程中,气泡脉动和辐射声压的变化。然而,在本文的研究中假定气泡质心静止,并未考虑声辐射力引起的气泡平移,也没有考虑气泡存在包膜的情况;另外,本文也没有研究气泡的非球形形变及其内部的声化学反应;将在未来的报道中对此进行深入讨论。

