融合共空间模式与脑网络特征的EEG抑郁识别

王怡忻，朱湘茹，杨利军，3

1.河南大学 数学与统计学院，河南 开封 475004

2.河南大学 认知、脑与健康研究所，河南 开封 475004

3.河南省人工智能理论及算法工程研究中心，河南 开封 475004

抑郁症是一种常见的精神疾病，表现为日常活动中的快乐感降低、无助、持续的情感低落、悲观和思维迟缓等[1]。研究显示抑郁症将成为人类的第二大疾病[2]。目前临床对抑郁症的早期诊断方法有许多明显的缺点，包括患者否认、敏感性差和主观偏见，导致诊断结果不准确，从而影响患者的及时治疗，导致病情延误。因此，有必要开发准确、可操作的抑郁检测方法。一般来说，与语言和面部表情相比，生理信号可以相对客观地反映中枢神经系统的动态变化，并已被应用于各种研究领域[3]。脑电信号（electroencephalography，EEG）包含了大量的生理、病理信息，是脑神经细胞生理活动在大脑皮层或头皮表面的总体反应。相比于脑磁图[4]、功能磁共振成像[5]和正电子发射断层扫描[6]等研究工具，EEG由于成本相对较低，便于记录，并且不能轻易伪造等优点，仍然是监测大脑活动的重要工具[7]，并逐渐被应用于多种疾病的辅助诊断[8-9]。

由于大脑活动的复杂性，EEG信号不是脑认知信号和干扰信号的简单叠加，而是非线性、时变信号，有必要获得高效低维EEG特征。常见的特征主要有时域、频域与空域特征。二分类任务下的空间滤波算法共空间模式（common spatial pattern，CSP）[10-11]一般被用于提取空域特征。Koles等人在1991年首次提出了用于EEG的CSP算法[10]，能够从多通道的脑电数据中提取出每一类的空间分布成分。利用协方差矩阵的对角化找到一组最优的空间滤波器进行投影，使得在最大化第一类方差的同时最小化另一类方差，从而得到具有较高区分度的特征向量。另一方面，由于图论分析技术被成功引入到脑功能网络研究中，复杂网络分析近年来日益成为脑电领域的研究热点。研究表明引入复杂网络模型能够帮助人们更好地理解脑网络结构之间的关系[12-13]。在Gonuguntla等人[13]的一项工作中，他们使用相位锁值（phase locking value，PLV）构建脑功能网络，并且进一步讨论了运动想象数据集上任务相关的网络差异，由此确定了重要节点和通道。综合以上两点，在本文工作中，首先进行了脑网络分析，使用PLV构建抑郁患者和正常对照的相位同步性功能网络，探索两种类别可能存在的不同连接模式，然后将CSP特征和网络特征进行融合用于抑郁识别。

多通道脑电信号往往含有大量的冗余信息，冗余特征会对算法的性能产生不利影响，导致计算复杂度高、过拟合、效率低等问题，因此需要从特征矩阵中筛选出更有代表性的特征。在实际应用中，存在多种特征选择策略，如皮尔逊相关系数（Pearson correlation）[14]、Relief算法[15]以及Fisher score（F-score）[16]。F-score本质上是通过计算单个特征的类间和类内方差的比值来衡量特征的辨别能力。F-score的值越大，区分能力越好。本文结合F-score方法和分类器依赖结构实现特征选择，既保证了所选特征子集和模型的识别能力，又节省了计算量。

随着深度学习的发展，通过计算机辅助抑郁症分类诊断有助于降低临床诊断的误诊率，帮助患者尽快获得正确的治疗。例如，Acharya等人[17]使用多层卷积神经网络（convolutional neural network，CNN）对15名健康受试者和15名抑郁受试者针对大脑右半球进行分类，分别获得了96%和93.5%的准确率。Li等人[18]利用EEG特征变换进行抑郁症识别。他们使用自回归模型和Hjorth算法提取功率谱密度和活性作为原始特征，并采用集成学习和深度学习两种不同的方法来处理这些特性，分别在五个频带和总频带上测试了支持向量机（support vector machine，SVM）和CNN分类器的性能。结果表明，脑电信号可以作为抑郁症识别的可靠指标，采用集成模型和功率谱密度特征时，最佳精度为89.02%，运用深度学习方法和活动特征的准确率为84.75%。Zhang等人[19]将脑电数据与包括性别和年龄在内的人口信息相结合输入到一维CNN中，获得了75.29%的分类精度。CNN[20]是一种被广泛应用于模式识别领域的高效模型。然而，由于CNN的状态只依赖于当前的输入，并不适合处理时序问题。而长短时记忆网络（long short-term memory，LSTM）[21]和门控制循环单元（gated recurrent unit，GRU）[22]由于结构特点无法实现并行计算操作，导致计算效率不如CNN。因此，本文提出将时序卷积网络（temporal convolution network，TCN）[23]用于脑电信号的抑郁识别，该模型不仅具有RNN（recurrent neural network）处理时间序列的特性，而且还保留了CNN可并行计算的特点。

受前人研究成果和神经学发现的启发，本文采用CSP算法提取特征，并根据PLV构建了脑功能连通性矩阵，提取脑网络特征，特征直观可见，便于对特征选择方法进行验证。利用F-score与分类器结合的方法对提取的特征进行优选，得到区分度高的最优特征集。具体的实验过程如图1所示。在抑郁数据集上进行实验评估，结果证明了本文方法的有效性。

1 共空间模式与时序卷积神经网络

1.1 共空间模式算法

共空间模式（CSP）算法[10-11]是一种高效的空间滤波算法，其目标是创建最优公共空间滤波器。如图2所示，CSP通过同时对角化两类任务协方差矩阵的方式得到最有区分力的特征向量。

具体过程如下：

（1）假设X1和X2分别为两类数据样本，计算两类数据的协方差矩阵R1和R2：

其中，tr(·)表示矩阵对角线上元素的和，即矩阵的迹。

然后得到混合空间协方差矩阵：

（2）应用主成分分析法，对正定矩阵Rc进行正交白化变换并且同时进行对角化处理。对R进行特征值分解：

其中，Uc表示特征向量矩阵，Λc为特征值降序排列构成的对角矩阵，转换后可以得到白化值矩阵为：

（3）构造空间滤波器。将P作用于R1和R2得到：

S1和S2有公共特征向量，且存在特征向量矩阵B和对角矩阵Λ1、Λ2满足如下条件：

其中，I是单位矩阵。

（4）计算投影矩阵。由于两类矩阵的特征值总和是1，那么一个类别有最大的特征值时，另一个类别有最小的特征值。白化EEG到与Λ1、Λ2中的最大特征值对应的特征向量的变换对于分离两个信号矩阵中的方差是最佳的。因此可以利用矩阵B实现两类问题的分类，得到空间滤波器即投影矩阵W为：

（5）将原始抑郁脑电数据集经过构造的相应滤波器W滤波可得特征ZM×N：

可选择ZM×N的前m行和后m行(2m＜M)作为原始输入数据的特征。

1.2 PLV相位同步性脑功能网络构建

认知过程不仅涉及到大脑各区域的活动，还涉及到不同功能区之间的信息传播和交互。从本质上说，连接模式能挖掘相关大脑区域之间的相互作用，且网络属性是反映信息的传播和加工的网络模式。网络构建的方法有很多，其中大脑同步活动分析以同步测量矩阵的形式捕捉大脑中的同步活动，近年来备受关注。研究表明，EEG信号在跨脑区的范围内存有相位同步关系，而并没有幅度上的同步关系，因此基于相位信息的同步性测量比基于振幅信息的测量更具有辨识力[24]。本文采用相位锁值（PLV）来测量两个脑区之间的相位同步信息。假设两个信号x(t)和y(t)的瞬时相位是φx(t)、φy(t)，PLV定义为：

聚类系数是衡量大脑功能分离程度的指标，指一个节点与其邻居节点之间存在的连接数与最大可能连接数的比例。节点i的聚类系数定义为：

式中，cij是邻接矩阵的两节点i和j之间的连接权重。

特征路径长度L是指网络中连通两个节点的最少边数。平均特征路径长度是所有网络节点间最短路径长度的平均值。对于加权网络，节点i和节点j之间的一条边的长度由边的权重的倒数表示。

其中，N为加权网络中的节点，Lij为任意两个节点i和j最短路径的边数。

全局效率Ge度量信息在整个网络中的传播程度，与网络中任意两个节点之间的最短路径长度距离成反比。

局部效率通过观察各子网络的连接情况来衡量区域专业化网络的能力，它提供了网络容错性的估计。设Gi表示包含第i个节点的所有相邻节点的子网络，局部效率为子网Gi的平均效率为：

式中，NGi表示子图Gi中的节点数。

中介中心性是一种常见的网络局部属性，用来衡量节点在图中的中心性大小：

其中，σmn(i)代表从节点m到节点n之间经过节点i的最短路径数，σmn是节点m到节点n的最短路径长度。

1.3 时序卷积神经网络

Bai等人[23]提出了时序卷积网络（TCN），该模型既具有RNN处理时间序列的特性，同时也保留了CNN的可并行计算特点。图3～图5为TCN模型的结构刻画。TCN模型中涉及因果卷积、膨胀卷积和残差连接三种结构，下面将具体介绍。

1.3.1 因果卷积

TCN模型中的时序特性主要由因果卷积实现。因果卷积（如图3所示）是用于处理时序问题提出的一种对于t时刻的预测值，不考虑任何未来的信息而只考虑之前t-1个输入的卷积模型，如式（16）所示：

可以看出t时刻的状态只与之前时刻的信息有关。但是因果卷积随着隐藏层增多，会带来梯度消失或梯度爆炸、训练复杂度提高等问题。因此，Oord等人又提出了膨胀卷积[26]。

1.3.2 膨胀卷积

膨胀卷积不同于CNN使用池化层，它是在卷积里注入空洞来增加感受野。如图4所示，对于相同的输入，膨胀卷积相比于因果卷积有更大的感受野。膨胀卷积允许输入存在间隔采样，采样率受膨胀系数d控制。d=1表示输入时每个点都采样，在网络各层之间，d随着深度的增加指数增长d=2i-1。对于一个一维输入序列x∈Rn和滤波器f:{0,1,…,k-1}，在序列成分s上膨胀卷积作用后定义为，其中k为滤波器大小，s-d*i代表过去的方向。

1.3.3 残差连接

残差连接通过前向神经网络和跳层连接实现，一般被用来解决网络退化问题。跳层连接就相当于执行了恒等映射，不会产生冗余的参数，也不会增加计算复杂度。TCN架构中的残差模块显示在图5，一个残差模块内包含两层膨胀因果卷积和非线性激活函数（ReLU），并对卷积滤波器使用权重归一化，利用spatial dropout进行正则化，防止过拟合。特别的，TCN在残差块的恒等映射之间添加1×1卷积filters，保证输入输出之间张量尺度相同。

1.4 F-score特征选择

通常，多个特征之间的相关性会导致特征共线性，从而进一步诱发冗余信息。冗余特征会对识别算法的性能产生不利影响。本文提出将CSP特征和脑网络特征结合起来的策略。简单地将所有特征集中在一起可能是一种次优操作，因此通过合理的特征选择策略从特征向量中筛除不相关的、冗余的特征，选择一个最优子集尤为重要。本文结合F-score特征判别准则，并利用分类器依赖结构来实现特征选择，以减轻特征多重共线性的影响[16，27]。在保证所选特征子集和分类器的识别能力提高的同时又节省了计算量。F-score本质上是通过计算单个特征的类间和类内方差的比值来衡量特征的辨别能力。若一个特征是具有鉴别力的，那么该特征与同一类别样本之间的方差应该尽量小，而与不同类别样本之间的方差应该尽量大，这样才利于分类和预测。本文给每个特征一个得分，第i个特征的F-score定义如下：

算法1 F-score特征选择算法

输入：训练样本特征集X=[X1,X2,…,XN]。输出：最优特征子集Fopt。

步骤1计算特征集X的所有F-score值，并按照降序排序得到排序后的特征集F。

步骤2初始化特征子集Fset。定义最佳分类结果为Accopt并初始化为0。将最优特征子集Fopt初始化为空。

步骤3从F中选择F-score值最高的特征向量。将选定的向量添加到Fset中。设n为Fset中单个样本的特征个数。

步骤4对Fset进行10折交叉验证，得到分类精度μ。如果μ≥Accopt,则用μ取代Accopt并更新Fopt。

步骤5重复步骤2到步骤4直到n＞N。

2 实验结果

2.1 数据集与预处理

本文收集了招募的69名志愿者的EEG数据。这些志愿者都是某大学本科生且均为右利手，实验前已获得知情同意。该实验根据《赫尔辛基宣言》进行，并得到了该学校伦理委员会的批准（HUSOM-2018-367）。所有志愿者有偿参与实验。他们完成对两个抑郁量表CES-D[28]和PROMIS[29]的评估，并填写了问卷。经过严格的筛选和匹配，根据两份问卷的得分情况，计算每位参与者两份问卷的总得分。将得分最高的30名学生作为高风险抑郁组，得分最低的30名学生作为低风险对照组。表1描述了所收集的数据集。EEG采集设备使用64个电极的国际标准脑电图帽，采样频率为500 Hz，最终筛选出有效的62个EEG通道进行进一步的实验研究，电极位置如图7所示。在线记录时使用FCz作为参考，离线时重新引用全球平均参考。通过在右眼上方放置电极获得一个通道的眼电信号（electrooculography，EOG）。所有电极间阻抗保持在10 kΩ以下。采用0.05～100 Hz带通滤波器对EEG和EOG信号进行滤波。采用独立成分分析方法对眼电伪影进行校正。

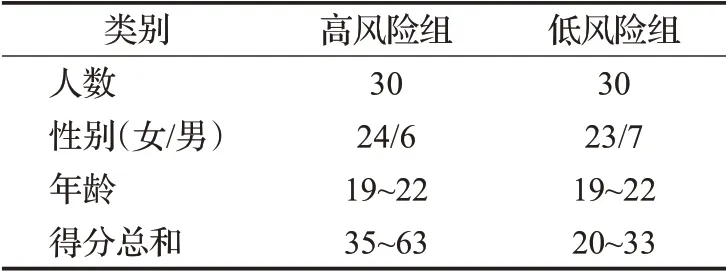
表1数据集描述Table 1 Dataset description

本文从所采集的60位志愿者的数据中截取25 000个数据点，截取后的数据通过分段方式扩充样本数。最终得到的每个样本的格式为63×500，其中63表示实验采用的通道数，500表示一个样本有500个采样点。另外，所有数据经过小波去噪处理，所有数据输入前经过z-score标准化处理。

2.2 PLV相位同步性分析结果

大脑区域之间的静息态功能连接可以提供有关抑郁病理生理学的更多信息[30]。本文使用图论量化脑网络。一个脑网络可以表述为一个图G=(V,E)，使用EEG电极作为网络节点，每个导联看作1个节点，通道之间的关系表示边。为了更好地反映大脑之间连接的紧密程度，根据PLV矩阵构建相位同步性功能网络并进一步可视化该网络。因为PLV的范围从0到1，所以PLV值可以作为同步性度量在加权网络分析中被用来表示连接强度。

研究表明，抑郁组和对照组的PLV值受频率带宽影响较大，因此需要将信号通过带通滤波到感兴趣的窄宽带上再进行分析[31]。此外，Fingelkurts等人[32]发现抑郁症几乎影响整个大脑皮层的活动，表现为在较宽的频率范围（0.5～30 Hz）内相对较大的脑震荡成分。并且抑郁症患者的脑电信号在δ、θ、α和β频带存在不同的振荡[32-34]。因此本文使用带通滤波器将信号过滤到这四个波段进行分析。功能连通性矩阵以二维矩阵的形式描述网络中所有通道对之间的连通性。抑郁组和对照组所有受试者的PLV矩阵在四个频段的平均结果显示在图8，PLV的值越接近于1说明信号之间的同步性越强。可以看到，高风险抑郁组和低风险对照组呈现出不同的连接模式，β波段的结果对比并不明显且连接程度相对较低，而θ和α频段显示出较大的连接强度。先前对于不同的同步性测量方法的相关研究表明，抑郁患者和正常对照组的功能连接在θ和α频带中显示出显著差异[31-34]。为了能够更直观地展现网络的特征，本文除了使用图论将五种网络特征作为评估网络的指标，还分别对PLV矩阵和五种网络参数使用进行t检验分析，结果表明四个频段下不同属性均具有显著性差异(p＜0.05)，具体数值如表2所示。相较其他两个频段，θ和α频段组成的网络连接统计学差异更明显。

表2 不同频段抑郁组和对照组不同属性的p值Table 2 p values of different features for depression group and control group under different bands

针对θ和α频段，图9是二维PLV矩阵的三维可视化。由于脑功能网络复杂且稀疏，有必要在网络构建过程中设定阈值。通过与所设阈值的比较，可去除相关性较小的边，使脑功能网络的连接关系更清晰。在本文中，阈值设置为0.75，保留PLV值大于0.75的连接强度来可视化脑网络。在脑网络拓扑图中，线条的粗细和颜色的深浅表示节点间的连接强度，线条越粗代表连接紧密程度越大。图9同时列出了两种频段下高风险抑郁组和低风险对照组连接强度大于0.75的电极通道对的个数、排名前三的电极通道对的名称，以及相应的PLV值。总体来看，α频段的连接程度高于θ频段。在θ频段，低风险对照组大脑右半球的连接紧密程度高于左半球，而高风险抑郁组的连接紧密度较为均衡。在α频段，抑郁组在左颞区的连接紧密度高于对照组。

2.3 基于不同方法的实验结果

实验通过Python3.7编程Keras框架Tensorflow后端实现。实验环境：Intel®CoreTMi5-1035G1处理器，16 GB内存，64位Windows10系统。

对数据集采用5次10折交叉验证方案来评估相应的分类性能。表3显示了不同特征的具体数量。整个分类过程包括以下步骤：

（1）将整个数据集划分为10个子集，选取9个子集作为训练集，其余作为测试集。

（2）根据Fopt选择最优特征组合。

（3）用训练集得到的最优特征对分类器进行再训练。

（4）用测试集的最优特征估计分类结果。

（5）重复前面步骤5次，计算平均分类准确率。

表3用于抑郁识别的各特征数量Table 3 Number of features used for depression recognition

对于TCN分类器，输入序列经过一维卷积核作用得到时序特征序列，最后引入全连接层，在当前时刻属于某一类别的概率由Softmax计算。所有激活函数均使用ReLU。卷积核大小设置为3，学习率设置为0.002。关于对比模型，本文采用非深度学习模型SVM，选用高斯核且惩罚因子C=2；对于深度学习模型，采用多层感知器（multilayer perceptron，MLP）和双向长短时记忆网络（Bi-LSTM）进行二分类对比实验，均使用Rmsprop优化器来最小化交叉熵损失函数。为了防止神经网络过拟合，在最后一层全连接后使用0.3的Dropout，批量大小为100。

使用四种分类器分别结合F-score进行特征选择，选出最优特征集Fopt再得到平均训练结果，结果如图10所示。本文所提模型在全频带内的准确率达到89.67%。从整体来看，本文所提策略不论在单个频段还是全频段的识别精度相比其他模型均有明显提升。α频段的分类精度都高于θ频段。在θ频段下，使用MLP和LSTM进行分类，比使用SVM得到的精度分别提升了约7个百分点和9个百分点。而使用TCN进行分类，精度则提升了约12.5个百分点。在α频段下，使用MLP分类的精度比SVM提升了约8个百分点，使用LSTM分类的结果精度提升了约9个百分点，而使用TCN的精度提升了约14个百分点。

需要注意的是，使用不同的特征选择方法可能会导致选择的最优特征子集存在一些差异，从而导致识别精度不同。例如，F-score利用可判别性作为选择最优特征子集的准则，而最大相关性-最小冗余（mRMR）[35]根据互信息的最大统计依赖准则选择好的特征，ReliefF[18]算法是一种典型的Filter式特征选择算法。因此本文进一步应用文献中的特征选择方法进行对比实验，分类器均采用TCN。结果如表4所示，虽然不同的特征选择方法所选择的最优特征子集不同，但本文提出的F-score结合TCN模型策略的最优特征集所得结果相比其他方法更好。

3 结束语

本文提出了一种基于EEG的脑网络拓扑结构和CSP特征融合的抑郁识别方法。通过计算多通道EEG信号的PLV邻接矩阵构建脑网络，可以将非线性的EEG信号转换为更加直观的网络参数，不仅有利于对信号的进一步研究，对临床诊断抑郁症也具有辅助作用。考虑到有一些冗余特征增加了噪声和训练难度，本文通过F-score方法结合深度学习模型TCN对融合特征进行简化，实验结果表明本文所提方法可以提高抑郁识别的性能。TCN既有RNN的时序性又有CNN的并行计算的特点，结合因果膨胀卷积以及残差连接，能够适应脑电信号的时序特征，克服网络的梯度问题。另外，PLV相位同步性分析的结果表明，抑郁高风险组和低分对照组在不同频段的不同脑区上呈现出不同的模式。