土钉横向抗剪效应对边坡稳定性的影响*

田 坤 朱鸿鹄 张诚成

(①长江三峡勘测研究院有限公司(武汉)，武汉 430074，中国)(②南京大学地球科学与工程学院，南京 210023，中国)(③南京大学(苏州)高新技术研究院，苏州 215123，中国)

0 引 言

土钉支护是边坡治理、基坑开挖的一种常用的支护形式，具有经济可靠、适用性强且施工快速简便等优点，自20世纪90年代以来在我国得到了迅速的推广和应用(陈肇元等，2000)。尤其在我国香港地区，已经成为最常用的边坡支护方式。一般而言，土钉由直径20～40mm的钢筋和外径75～150mm的水泥灌浆体所组成。土钉长度多为3～20m，与水平面呈10°～30°的斜向下倾角。

在国内外各类设计规范中，土钉对边坡的支护机理一般可概括为：通过与土体接触面上的黏结力或摩擦力，使得土钉被动受拉，反过来给土体以约束加固或使其稳定(Zhu et al.，2012；Zhang et al.，2014；Xu et al.，2018；阙云等，2021)。但是在实践中发现，土钉在土体中所受内力更为复杂，不仅受到沿土钉轴向的拉力，还受到垂直土钉的剪力(因侧向土压力作用于土钉上)，以及坡体稳定与不稳定区过渡带处的弯矩作用(何建勇等，2004)。许多学者指出，土钉所受轴力对提高边坡稳定性起着决定性的作用，土钉在破坏时的剪力仅占轴力的10%以内，其抗弯、抗剪刚度对土体加固效果可以忽略(Jewell et al.，1990；Juran et al.，1990)。除了法国，各国的土钉边坡设计规范中均沿用了这一保守假设，未考虑土钉的抗剪效应(Juran et al.，1990)。但是在一些黏土质边坡中，土钉在边坡达到极限状态前出现了较明显的横向变形，说明此时抗剪效应已经开始发挥作用，与此同时，在室内模型试验中这一现象也常被观测到(Bridle et al.，1997；Shiu et al.，2005；Zhou et al.，2008；Zhang et al.，2013；Zhang et al.，2014；Zhu et al.，2015；Sabermahani et al.，2017；姜振泉等，1996)。近年来，支护工程中逐渐出现了GFRP等新型土钉，人们发现它们的抗弯强度和抗剪强度对提高边坡的稳定性也有一定贡献(Yeung et al.，2005)。数值模拟结果也显示，边坡的稳定性受到土钉横向抗剪效应的影响(Shiu et al.，2005；Zhou et al.，2008；王媛媛等，2006)。所以，为了更好地发挥土钉支护的作用，需要对土钉的抗剪效应进行更加深入的分析。

本文基于常规的极限平衡法，通过一系列算例定量分析了土钉支护的抗剪效应对边坡滑裂面位置和安全系数的影响，揭示了土钉支护边坡的受力特点和土钉设计时需要考虑的因素，为土钉设计及施工提供参考依据。

1 考虑抗剪效应的土钉支护边坡稳定性分析

目前用于边坡稳定性分析的方法主要有极限平衡法、有限元分析法、地质条件分析法等。其中极限平衡法是岩土工程领域最早和最流行的数值分析技术之一(吕爱钟等，2022)。该方法假定均质土坡破坏时的滑动面为圆弧形，通过对滑体进行条分，分析各土条受力，建立静力极限平衡方程或力矩极限平衡方程，通过迭代得到最小安全系数和临界滑动面。根据不同的土条受力假定，极限平衡法主要分为瑞典条分法、Bishop法、Janbu法、Morgenstern-Price(M-P)法等(陈祖煜，2003)。其中在M-P算法中，由静力极限平衡方程和力矩极限平衡方程可分别得出两个安全系数，即M-P(力)解和M-P(力矩)解。

在传统的土钉支护边坡设计中，利用极限平衡法分析土条受力时，忽略土钉的抗剪力作用。但研究发现，对于一些土质较软、会发生较大变形的土钉支护边坡，土钉的横向抗剪效应对提高边坡的稳定性有一定的贡献，在计算中考虑土钉抗剪作用可得到更符合实际情况的安全系数。

在边坡稳定性的条分法分析中，对于土条受力，可建立如下水平方向力的平衡方程：

∑(EL-ER)-∑(Nsinα)+∑(Smcosα)=0

(1)

式中：Σ(EL-ER)为条间法向力；N为土条底面的法向力；Sm为土条底面的抗剪强度；α为土条底面切线方向与水平方向夹角。

极限平衡方程建立在土条底部折减后的平均剪应力基础上(陈祖煜，2003；Krahn，2008)，所以抗剪力为：

(2)

式中：Ssoil为土条底部的剪应力；FoS为折减系数；c和φ为土体的黏聚力和内摩擦角；σ为土条底部的正应力；l为土条底部的长度。

当土体中设置了土钉等加筋体后：

(3)

式中：Snail为加筋体提供的加固力。由于土钉的刚度远大于土体，且土钉在边坡有滑动趋势时瞬时发挥作用，所以加固力不必加以折减(Krahn，2008)。

为简化起见，本研究统一采用无量纲指标κ来表述土钉的抗剪效应：

(4)

式中：FS为土钉所受的剪力；FT为土钉所受的轴力(假设其方向平行于土条底面)，两者的比值κ定义为土钉的抗剪效应因子(κ=0即不考虑该效应)。如图1b所示，当考虑土钉的横向抗剪作用时，在土条底面与土钉的交点处增加一个剪力，将该力加入土条静力平衡方程中。

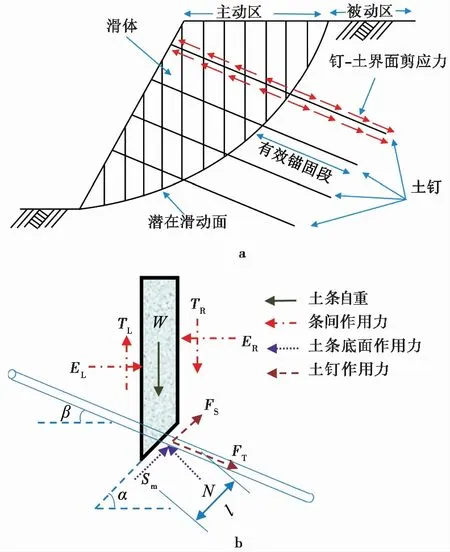
图1 土钉支护边坡中土钉和土条的受力示意图Fig.1 Loading mechanism of the soil nail and the sliding soil mass in a soil-nailed slopea.常规土钉边坡设计图；b.考虑横向剪力的土条受力图

表 1 用于算例分析的土钉边坡参数Table1 Material parameters used in this study

2 算例分析

为了系统分析土钉的抗剪作用对于边坡安全系数及滑动面位置的影响，本文基于Geo-Studio软件中的Slope/W模块(Krahn，2008)开展了一系列极限平衡分析。计算中采用文献Juran et al.(1990)中的边坡模型。该边坡的初始坡角α取55°，土体采用莫尔-库仑模型模拟，相关分析参数见表 1。由条分法计算可知，该边坡的安全系数为1.1左右，易发生浅层滑动。为了对其进行加固，设置了等长的7排水泥灌浆土钉，土钉长20m，倾角β均为15°。经过加固后，边坡安全系数提高到了2.0左右。利用Slope/W建立了如图2所示的二维分析模型。采用4种常见的边坡稳定性分析方法(包括瑞典条分法、Bishop法、M-P法和Janbu法)进行了一系列的参数分析，以考察土钉的抗剪效应因子κ以及土钉长度L、倾角β等对边坡稳定性的影响规律。

图2 边坡计算模型(单位：m)Fig.2 Analysis model of the slope(unit：m)

图3 不同抗剪效应因子时土钉倾角与边坡安全系数关系曲线Fig.3 Variations of factor of safety with nail inclination under different shear capacity factorsa.κ=0；b.κ=0.1；c.κ=0.3；d.κ=0.5

表 2 不同抗剪效应因子对应的最优土钉倾角和边坡安全系数Table2 Optimum nail inclination and calculated factors of safety for different shear capacity factors

2.1 土钉最优倾角及边坡安全系数

图3a至图3d分别显示了在抗剪效应因子κ为0、0.1、0.3、0.5的情况下，边坡安全系数随土钉倾角(0°～65°)变化的规律。该结果显示，4种边坡稳定性分析方法得到的安全系数一致性较好，其中Janbu法得到的安全系数一般为最小，其次是瑞典条分法，Bishop法和M-P法的结果较为接近，符合预期(Krahn，2008；陈祖煜，2003)；当不考虑土钉的抗剪效应或抗剪效应较小时，随着土钉倾角的增加，安全系数呈现先变大后变小的趋势，说明存在使得边坡达到最稳定状态的最优土钉倾角βopt。表 2列出了在土钉最优倾角条件下的边坡最大安全系数。该表显示，当土钉的抗剪效应因子从0增大到0.5时，坡体的最大安全系数也逐渐增大，而土钉埋入坡体的最优倾角也从25°增大至65°以上。这说明，在土钉极限长度范围内，增加土钉倾角使得抗滑力明显提升，有利于土钉抗剪作用的发挥，这对于提高边坡稳定性有着极其重要的影响。

2.2 土钉长度及边坡安全系数

图4a至图4d分别表示抗剪效应因子κ为0、0.1、0.3、0.5时，边坡安全系数随土钉长度(0～40m)变化的规律。该结果显示，在土钉倾角均为15°的条件下，土钉长度和边坡安全系数之间呈明显的正相关关系，增加土钉长度可显著提高边坡的安全系数。反过来，在土钉倾角为βopt时，土钉长度增加意味着土钉所受剪力增加，抗剪效应增强。当安全系数较大后，坡体可视为完全稳定，此时继续增加土钉长度会造成材料浪费。另一方面，由于土钉的抗拔力不仅取决于钉-土的界面摩擦力，还和土钉本身的抗拉强度有关。需要指出的是，土钉长度对于边坡安全系数的贡献存在一个极限值。当土钉过长(超过土钉极限长度)时，破坏模式从土钉拔出破坏变为土钉拉断破坏，从而造成不合理的设计(何建勇等，2004)。图5显示，在土钉长度相同的条件下，κ越大则安全系数也越大，但这种效应随着κ的增大逐渐减弱。这说明，土钉横向剪力只能在有限的范围内提高边坡的安全系数，提高百分数约为18%～30%。

(5)

式中：η为土钉横向剪力增益率；FoSmax为不同抗剪效应因子下安全系数的最大值；FoSmin为不同抗剪效应因子下安全系数的最小值；FoSini为无抗剪效应因子下的安全系数，在图5中即为安全系数最小值。

图4 不同抗剪效应因子时土钉长度与边坡安全系数的关系曲线Fig.4 Variations of factor of safety with nail length under different shear capacity factorsa.κ=0；b.κ=0.1；c.κ=0.3；d.κ=0.5

图5 不同钉长时抗剪效应因子与边坡安全系数的关系曲线Fig.5 Variations of shear capacity factor with factor of safety under different nail lengthsa.L=15m;b.L=20m;c.L=25m

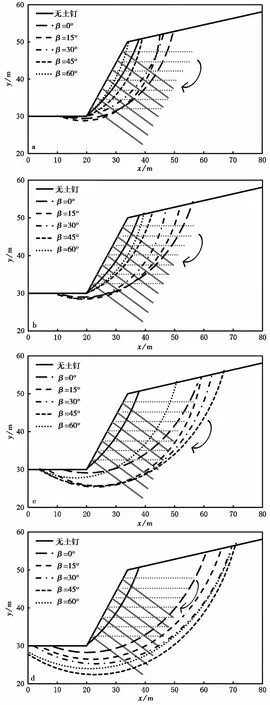
图6 各抗剪因子条件下土钉倾角与相应的滑面位置Fig.6 Variations of the slip surface with nail inclination under different shear capacity factorsa.κ=0；b.κ=0.1；c.κ=0.3；d.κ=0.5

2.3 边坡滑面位置

边坡临界滑移面的生成是滑坡演化过程的重要标志，滑移面的位置直接影响安全系数的大小，并对边坡加固工程设计有极其重要的指导作用(闫国强等，2021；赵云鹏等，2021)。为了分析土钉抗剪效应对滑移面位置的影响，本文从土钉倾角和长度两方面考虑，模拟土钉抗剪效应因子变化情况下，边坡潜在滑移面位置的变化规律以及相应的安全系数。

2.3.1 土钉抗剪效应和倾角对滑面的影响

各抗剪效应因子条件下土钉倾角对滑面影响的分析结果如图6a至图6d。结果显示，无土钉加固情况下，滑面由坡顶平滑延伸至坡脚，呈现为坡脚圆。在设置土钉后，圆弧形滑面由坡脚圆变为中点圆。若不考虑土钉的横向抗剪效应(κ=0)，随着土钉倾角逐渐增大，滑动面又逐渐向坡面移动，圆弧形滑面从中点圆向坡脚圆过渡。

当土钉抗剪效应较为明显时，边坡破坏呈现出典型的中点圆特征。抗剪效应越大，滑移面越深、越长，坡脚处滑面甚至可以延伸至坡前约15m处。此时，有数根土钉未与滑面相交，说明它们未对边坡起加固作用。深层滑坡的出现是判断土钉支护边坡中横向抗剪作用是否充分发挥的一个重要标志。此外，随着抗剪效应的增大，最深滑移面所对应的土钉倾角也会变大，从抗剪效应因子为0时的15°增加至45°。

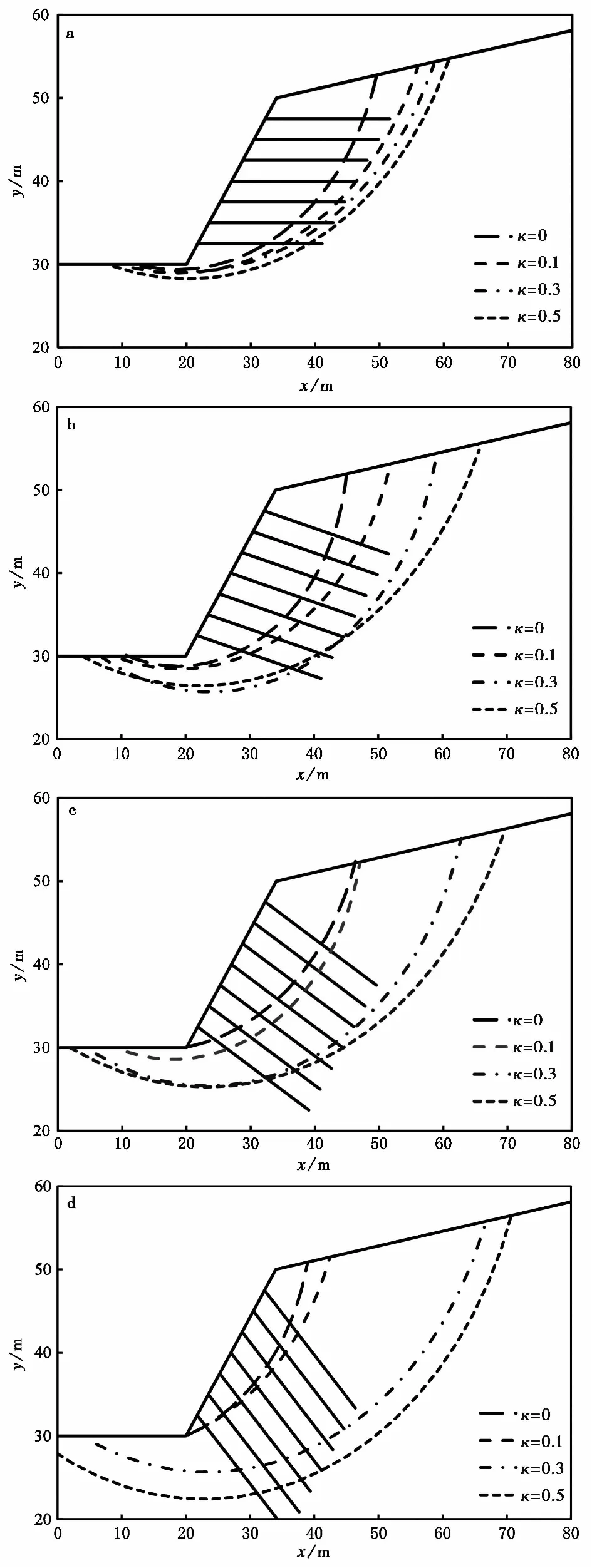
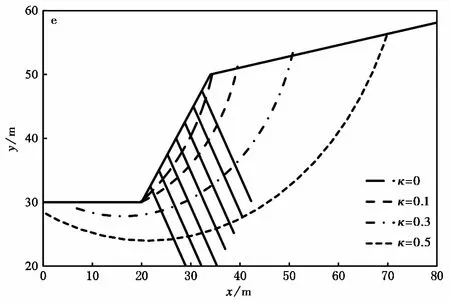
图7 各土钉倾角条件下抗剪效应因子与相应的滑面位置Fig.7 Variations of the slip surface with shear capacity factor under different nail inclinationsa.β=0°;b.β=15°;c.β=30°;d. β=45°;e.β=60°

图7结果显示，在土钉倾角不变的情况下，随着抗剪效应因子的增大，滑移面逐渐向后移动。在土钉倾角从0°～60°的增大过程中，抗剪效应对滑移面位置的影响急速上升。在本文的数值模型中，当土钉倾角为0°时，抗剪效应对坡顶滑面位置的影响范围为10m左右；而当倾角为45°时，土钉抗剪效应对坡顶滑面位置的影响范围达30m，为坡高的1.5倍。需要说明的是，土钉支护通常适用于高陡危险边坡。根据国家规范《复合土钉墙基坑支护技术规范》(GB 50739-2011)，土钉与水平面夹角一般为5°～20°。因此，本研究中0°和65°取值都属于工程不常见的极端工况，但为了充分说明土钉倾角的重要作用，故参数分析中的β值取0°～65°。

图8 各抗剪效应因子条件下土钉长度与相应的滑面位置Fig.8 Variations of the slip surface with nail inclination under different shear capacity factorsa.κ=0；b.κ=0.1；c.κ=0.3；d.κ=0.5

图9 不同土钉长度条件下抗剪效应因子与相应的滑面位置Fig.9 Variations of the slip surface with shear capacity factor under different nail lengthsa.L=10m；b.L=15m；c.L=20m；d.L=25m

2.3.2 土钉抗剪强度和长度对滑面的影响

各抗剪效应因子条件下土钉长度对滑面影响的分析结果如图8a至图8d。分析结果表明，在不同抗剪效应因子下，土钉长度的变化对坡顶滑面初始点位置的影响范围较小，均为10m以内。

从图8a至图8d也可以看出，如果保持土钉长度不变，随着抗剪效应因子的增加，滑面会后移。在土钉的抗剪效应因子为定值时，滑面也会随着土钉长度的增加而后移，出现深层滑移趋势；而在抗剪效应微弱的情况下，这样的规律并不明显。

3 结 论

本文通过一系列极限平衡算例，分析了土钉横向抗剪作用对边坡稳定性的影响规律。初步结论与建议如下：

(1)在考虑了土钉横向抗剪效应的情况下，基于4种极限平衡法分析了边坡稳定性，包括瑞典条分法、Bishop法、Janbu法和Morgenstern-Price法，所得的边坡安全系数及其变化规律基本一致，其中Janbu法所得安全系数最小。

(2)本文提出采用抗剪效应因子来量化土钉的抗剪作用。随着土钉的抗剪效应因子的增大，边坡安全系数也相应提高，但是增长只发生在一定范围内。当土钉达到最优倾角时，边坡稳定性最高，该倾角随抗剪效应因子的增大而增大。因此，若需充分利用土钉的抗剪强度，则应适当增加土钉的倾角。

(3)当土钉抗剪效应较为明显时，边坡滑面呈现出典型的中点圆特征，此时边坡破坏形态为沿深部的滑移。将土钉以较大的角度(30°～45°)设置于坡体内时，土钉的抗剪效应对边坡滑移面位置的影响较高。

(4)土钉长度的增加对改善边坡稳定性有着明显的作用，使得滑面后移，但土钉长度过长则会造成材料的浪费，并在边坡失稳前发生土钉拉断。如果保持土钉长度不变，随着抗剪效应因子的增大，滑面也会明显后移。