矿山机械的磁性液体阻尼减振实验研究
朱姗姗,初 琦,杨晓雪,黄 宇
(北京工业职业技术学院机电工程学院,北京 100042)
1 前言
矿山机械在运转中产生的有害振动是不可避免的。在采矿工程中高效低污染的作业方式,对可持续发展具有划时代的意义。矿山机械在工作环境中,外部阻力、空气中的气流、外部环境的噪声、飞虫的扰动都能引起机械臂产生不必要的振动[1-5]。由此,设计一款质量轻、体积小的减振器来抑制机械臂的受迫振动能有效提升机械作业精度。
在矿山机械技术开发的早期,M.seelinger 等人设计了一款基于摄像机空间视觉的导航系统,采用等离子移动喷嘴、六自由度机械臂,机械臂的空间运动轨迹能够使机器在合理的范围内工作,能够有效节省机器的运行时间并降低工作成本,但还没有对机械臂在工作环境中所受扰动进行减振控制[6-8]。本文应用功能材料磁性液体的二阶浮力原理,设计一款应用于矿山机械的磁性液体阻尼减振器,有效降低机械臂在工作过程中的受风扰动,一定程度上能够提升机械臂的作业精度。
对于磁性液体应用于减振方面的研究,美国NASA 宇航局研制了一款无线电天文探测器的减振器,用于抑制卫星中挠性构件的扰动振荡。日本和德国的一些科研工作者对不同结构类型的磁性液体减振器进行动力学研究并开展相关的减振实验工作,在航空航天、建筑施工、机械工业等领域得到应用并推广[9-15]。国内的科研学者主要研究了磁性液体的自悬浮特性及磁化特性等基础性能,对磁性液体减振器的结构设计和实验研究还有大量的工作需要开展。
本文结合矿山机械的工作特点,即在工作环境中振幅小、频率低的特点,设计了一款减振器。与传统行业的减振器相比,这款减振器的壳体采用轻质材料3D 打印成型,使得减振器自重轻,同时无需对减振器设置外部激励,对机械臂的受扰动振动的情况有一定的抑制作用,为精准作业提供了一定的理论依据。
2 减振器工作原理
2.1 磁性液体的理论基础
在伯努利方程中,对于普通流体的粘滞效应忽略不计,假设理想流体为不可压缩状态,则普通流体速度与压强之间的关系为
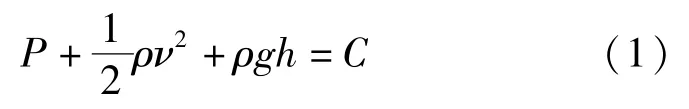
式中,P为流体的任意一点的压强,ρ在式中为该流体的密度,ν为流体中这一点的流速,g为重力加速度,h为流体中这一点的相对高度,C表示常数。磁性液体在伯努利方程中既遵循能量守恒定律,又应当考虑磁场因素的作用。而磁性液体在非均匀磁场力作用下,在微观场中的粘滞效应会随磁场发生相应的变化。根据牛顿第二定律,磁性液体的运动方程为
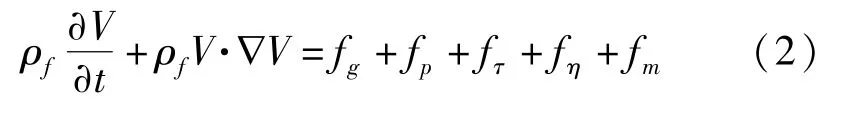
式中,ρf为密度,V为速度,∇V为速度梯度,fg为密度ρf与重力加速度g的乘积,即:

fp为压力梯度,是磁性液体在流动方向上单位长度内压力的变化量,即:

fτ为附加力,磁性液体既具有磁性颗粒,又具有胶体溶液,是包含固液两相的流体。有外加磁场时,在外加磁场的作用下,液相和固相由于滞后会产生速度差。液固两相速度差所产生的相对运动有一定的延迟,在不考虑微观效应时,此项可不予考虑。
fη为粘性力,由于受到磁粘效应的影响,由磁场作用下磁性液体的粘度ηh与速度V决定,在均匀磁场中则表现为

fm为磁场力,外磁场作用于磁性液体的磁场力,通常在磁场分布非均匀时产生,由磁化强度M、真空磁导率和磁场强度决定,也即Kelbin 力密度:

将式(6)代入到式(1)中可得:

如果不考虑外磁场的改变所导致的胶体溶液内部固相颗粒转动的情况,也即假设磁性液体是内禀性的,则:

此时磁性液体的磁化强度和磁场平行,结合Leibniz 公式,取导数可得:
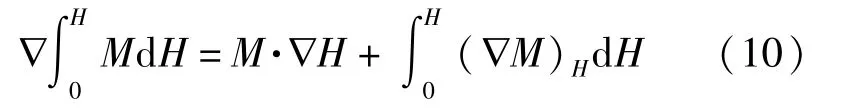
对于密度恒定不变的磁性液体,即∇·V=0,由于温度T同样会影响磁化强度M的大小,因此计算时应加以考虑,可得:
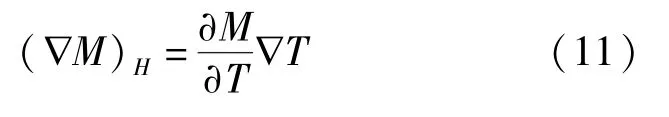
将式(11)代入到式(10)可得:

假设没有温度梯度,即∇T=0;且磁性液体温度低于居里温度,即:=0,则非定常流动为
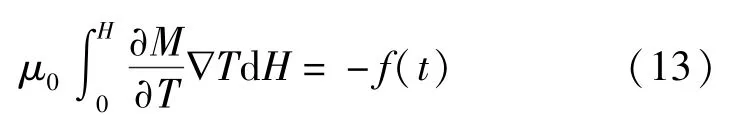
考虑到重力场为有势场,假设磁性液体与参考平面之间的直线距离为h,则:
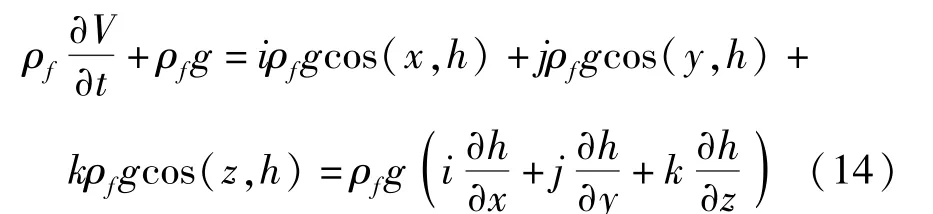
则:
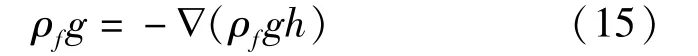
假设流动具势,则V=0,令

由矢量恒等式可得:

将以上推导公式代入,并合并∇项得:

如果流动定常,则f(t) =0,且=0,则可得定常伯努利方程为

2.2 电磁阻尼耗能理论基础
通过电磁感应原理将振动能量转化为电能,将振动能量消耗,并且存在着电磁阻尼,研究电磁阻尼在不同外部振动激励作用下,对振动能量的耗散衰减的幅度,在耗能块随主质量块振动过程中,磁性液体减振器通过永磁体在减振器壳体内与磁性液体之间的相对运动所产生的摩擦耗散主质量块的振动能量。根据楞次定律,只要穿过闭合电路的磁通量发生变化,闭合电路中就会相应地产生感应电流,闭合电路中所产生的感应电流的磁场总要阻碍引起感应电流的磁通量的变化。由此,在磁性液体阻尼减振器的非导磁壳体的外部缠绕电磁线圈,通过感应电流产生的磁场对引起感应电流磁通量变化的耗能块的阻碍效应,可以有效控制耗能块与磁性液体之间相对运动。同时,通过控制电磁线圈的电流大小,也可以调节电磁线圈产生的磁场对耗能块与磁性液体之间的相对运动,有效控制减振器的阻尼效应。
磁性液体阻尼减振器的结构设计主要包括三个部分,其中有非导磁性壳体,用来装载磁性液体和永磁体耗能块;惯性质量永磁体耗能块和给耗能块提供回复力的磁性液体和电磁线圈,具体如图1所示。同时考虑到所设计的减振器主要应用于长直挠性部件上,为保证减振性能稳定有效,减振器壳体选用轻质树脂材料,采用3D 打印加工,长直挠性部件选用铜板。

图1 减振器结构
3 磁性液体的减振实验研究
3.1 实验装置和相关参数
为避免外部磁场的干扰作用,在减振实验中的长直挠性件选用非导磁磷铜板,实验装置如图2所示。减振实验台主要包括减振器、位移传感器、数据采集仪、软件分析显示器、电脑等,具体如图3所示。实验中所使用的磁性液体为煤油基Fe3O4,其密度ρ=1.76 g/cm3。

图2 挠性件减振装置
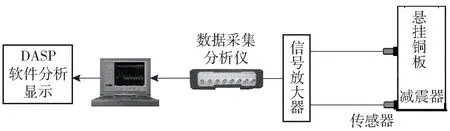
图3 减振实验台
3.2 实验内容
实验中,先将减振器壳体固定在铜板的末端。此时非磁性壳体内不放置磁性液体,电磁线圈不通电流,对铜板的末端施加3 mm 的初始振幅,令铜板自由振动,采集当前振动的振幅信号如图4所示;然后在电磁线圈仍然不通电流的情况下在减振器壳体内装载永磁体耗能块,同时注入磁性液体,磁性液体注入量由0.5 g、0.6 g、0.7 g…1.5 g 依次增加,分别采集到铜板振幅的衰减信号如图5所示。从图中数据可以看出,减振器在对铜板振幅的衰减幅度表现不一,由此,在相同的振动条件下,减振器的减振性能与磁性液体注入量有直接的关系。在此实验中,磁性液体的最佳注入量约为1.2 g。减振器电磁线圈不通电时,在相同的振动条件下,磁性液体的注入量存在最佳值。
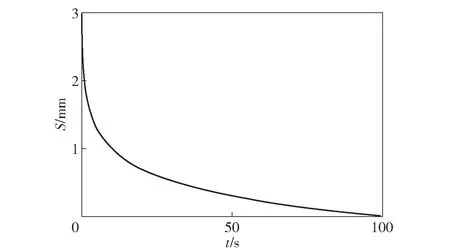
图4 未添加磁性液体的铜板振幅
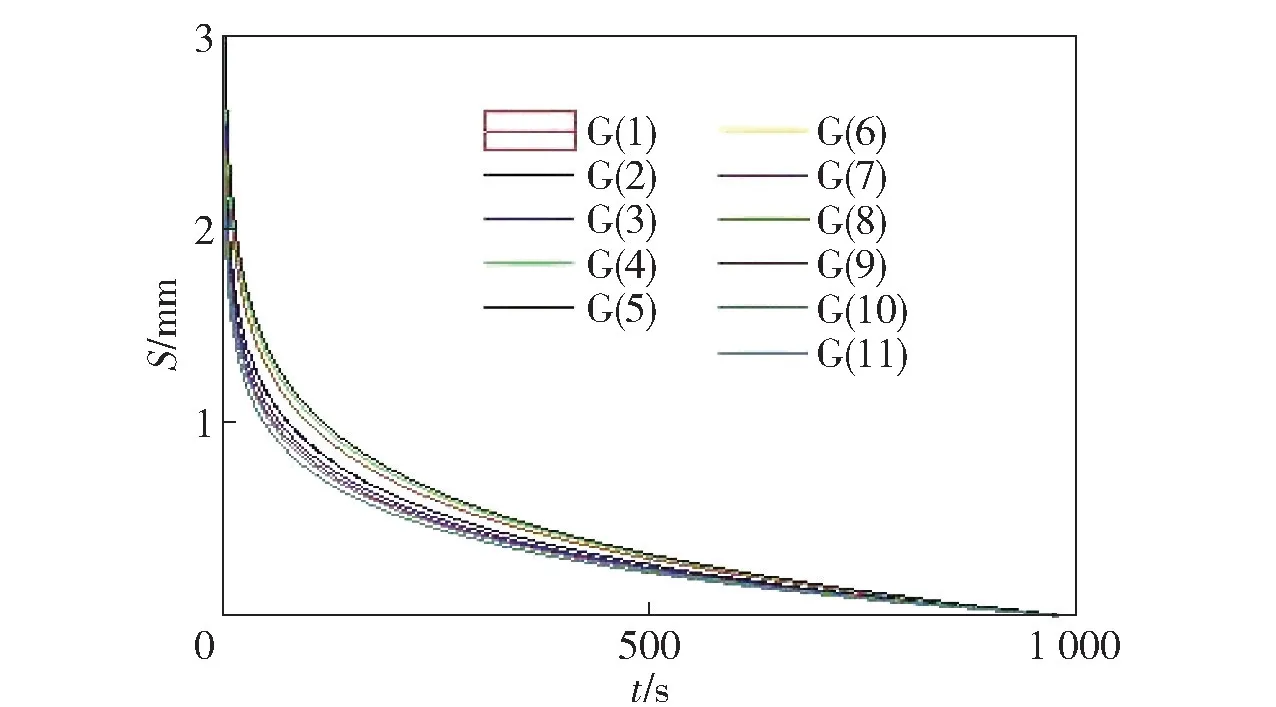
图5 不同磁性液体注入量的减振效应
在减振器壳体内注入约1.2 g 磁性液体,装载永磁体耗能块,对铜板末端施加3 mm 初始振幅,令铜板自由振动。对电磁线圈分别通入1 A、1.5 A、2 A、2.5 A 电流,分别采集铜板的振幅信号如图6所示。从图中数据可以看出,在相同的振动条件下,电磁线圈通入的电流值的电流时,产生的减振性能也不一样。根据楞次定律,只要穿过闭合电路的磁通量发生变化,闭合电路中就会产生感应电流。一方面,闭合电路中磁通量变化的程度不一样,电磁线圈中所产生的感应电流也不一样,感应电流的磁场总要阻碍引起感应电流的磁通量的变化;另一方面,电磁线圈中通入电流值大小不一样,电磁线圈对永磁体耗能块和磁性液体的磁场力也不一样。
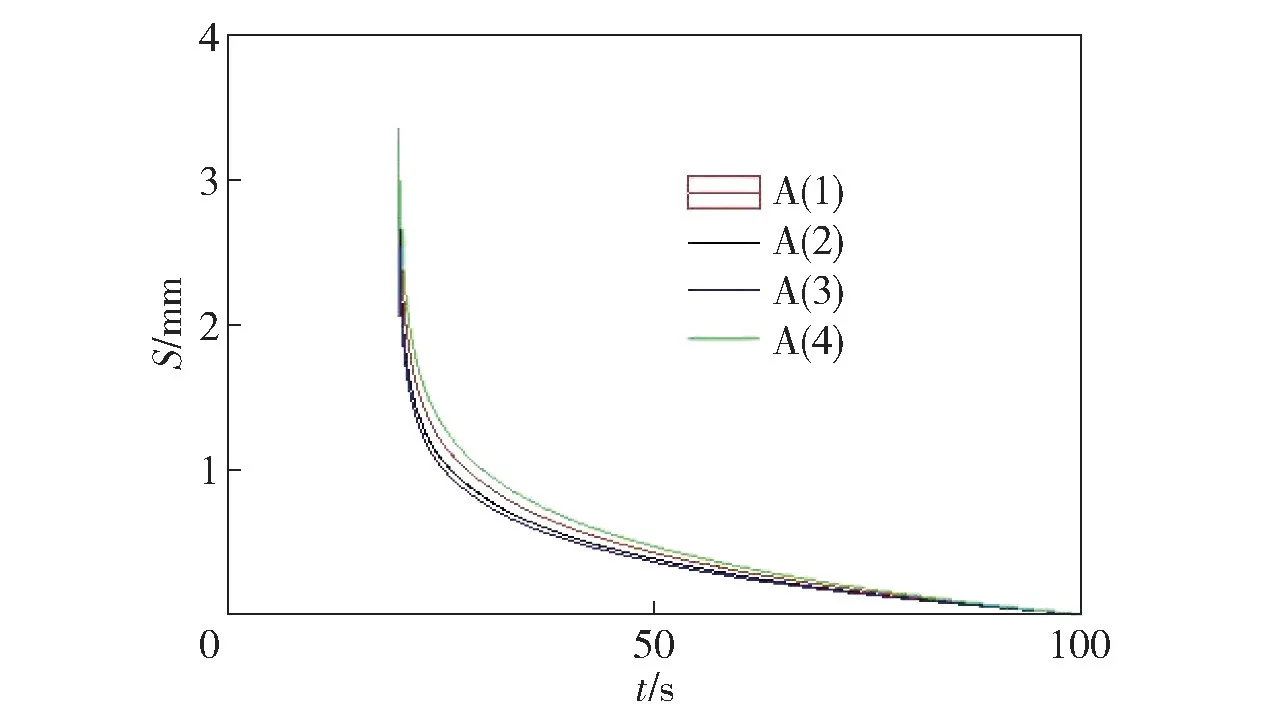
图6 不同通电电流的减振效应
对电磁线圈中通入电流的大小对应着外加磁场施加于磁性液体和永磁体耗能块磁场力的大小,减振效果不会一直随着磁场的增大而增强,而是会存在一个过渡区间,在这个过渡区间之前,减振性能会随着外部磁场也就是电磁线圈中通入的电流的增大而增强,当磁场强度超过这个过渡区间后,减振器的减振性能会逐渐减弱,但是在振动消失的时间维度上的差异表现得均不明显,而是在振幅衰减的幅度上存在明显的差异。
当振源为正弦激励时,电磁线圈不通入电流,减振器内注入不同体积的磁性液体量时,减振效果也不一样,具体如图7所示。图中S1 为未注入磁性液体时,铜板的振动情况。S2 和S3 分别为注入0.8 g和1.2 g 磁性液体时铜板的振动情况。

图7 正弦激励时不同磁性液体注入量的减振情况
在不改变外部激励频率时,改变磁性液体注入量,减振性能根据注入量的变化也会相应地产生变化。减振器的减振性能存在最佳减振区间,在不同的外部激励频率下,磁性液体注入量在最佳减振区间内使减振效果达到最佳。
4 结论
(1)在相同的振动条件下,减振器的减振性能与磁性液体注入量有直接的关系。减振器电磁线圈不通电时,在相同的振动条件下,磁性液体的注入量存在最佳值。一方面,由于随着磁性液体注入量的增加,减振器的自重也随之增加;另一方面,磁性液体注入量增大,与永磁体耗能块的摩擦耗能效应也发生变化。
(2)对电磁线圈中通入电流的大小对应着外加磁场力的大小,减振效果不会一直随着磁场的增大而增强,而是会存在一个过渡区间。在这个过渡区间之前,减振性能会随着外部磁场的增大而增强,当磁场强度超过这个过渡区间后,减振器的减振性能会逐渐减弱。但是在振幅消失的时间维度上的差异表现不明显,而是在振幅衰减的幅度上存在明显的差异。在矿山机械的挠性构件减振器的设计中,应当依据构件所受的扰动情况,设置合理的电磁线圈的通电电流。
(3)当磁性液体注入量不变,外部振动激励频率发生变化时,电磁线圈通电电流会影响减振器的减振效果。在通电电流不变时,不同的激励频率得到不同的振幅衰减程度,同时,振动消失的时间也不一致。在振动消失的时间维度上的差异表现得均不明显,而是在振幅衰减的幅度上存在明显的差异。

