露天矿山运输车辆横向非线性模型预测控制研究
王 斌,袁希文,张 乾,胡云卿,李 程
(中车株洲电力机车研究所有限公司,湖南 株洲 412001)
0 引言
采用无人驾驶矿山运输车辆对降低煤炭开采成本、提高运输效率、减少事故发生具有重要的现实意义[1]。矿山运输车辆的车辆运动控制技术是实现无人驾驶的核心技术之一,车辆横向运动路径跟踪控制技术属于一项关键的车辆运动控制技术。
当前,国内外学者在车辆路径跟踪控制领域进行了大量研究。文献[2]建立了车辆的横向运动学和动力学模型,设计了基于动力学模型的转向反馈控制器,并将道路的弯曲变化作为扰动项设计前馈补偿策略来消除系统的稳态误差。文献[3-13]研究了车辆横向控制的线性二次型调节(linear quadratic regulator,LQR)控 制 器 设 计 方 法 和MPC(model predictive control)控制器设计方法。文献[3]基于车辆的横向运动学模型将非线性运动学模型进行近似线性化处理,设计了LQR控制器;并基于横向偏差和横摆角偏差模型,设计了线性MPC控制器。文献[4]基于车辆横向动力学模型和转向控制器延迟模型设计多点预瞄的LQR控制器,通过求解Riccati方程得到LQR控制器增益矩阵的理论解,并对该方法的系统稳定性进行了分析。文献[6]针对矿井车辆在巷道实时避障过程中参考轨迹的平滑性问题以及在轨迹跟踪过程中转向角突然变化对矿井车辆结构和转向部件造成的损伤问题,利用曲线坐标系变换,将车辆运动学模型转换为横向偏差和横摆角偏差的模型,设计了一种空间模型预测控制(spatial model predictive control,SMPC)横向控制器。文献[7]在Frenet坐标系下建立了横向运动学模型,将转向控制器的延迟模型简化为一阶惯性环节和纯时滞环节,并在建立MPC模型中考虑转向控制器的延迟模型。文献[11]基于运动学模型建立MPC模型,目标函数中考虑横向偏差、横摆角偏差和车轮转角增量的影响,并采用模糊规则的方法设计目标函数的权重值。文献[14]针对驾驶过程中存在的延迟和前视距离等因素,设计了一种时间延迟动态预测策略,根据运动学模型预测延迟后的车辆运动方向和位置信息,然后基于行驶方向和轨迹方向之间的偏差值进行横向跟踪控制。目前,尚未有文献针对露天矿山运输车辆在复杂多变工况下的路径跟踪MPC控制进行研究。
在矿区复杂多变的场景中,矿山运输车辆高速直线行驶时,容易出现高速摆动的现象;在大曲率转弯、S形线路行驶、倒车时,容易出现横向偏差较大、横摆角偏差过大的现象。对此,本文基于车辆横向运动学模型设计了一种非线性模型预测控制(nonlinear model predictive control,NMPC)控制器。其在目标函数中考虑横向偏差、横摆角偏差和转向角变化率,并设计依赖速度的目标函数的自适应权重系数;针对转向控制器的延迟现象,设计了一种转向延迟补偿策略。最后,通过矿山运输车辆实车试验,验证了所提方法的可行性。
1 车辆横向运动学模型
车辆横向运动学模型如图1所示。大地坐标系下,(x(t),y(t))为车辆前轴中心坐标;φ(t)为横摆角;δ(t)为前轮转向角,其中δ(t)>0表示左转向,δ(t)=0表示直行,δ(t)<0表示右转向;L为轴距;v(t)为车速。由图中所示几何关系可以得出车辆运动学模型状态方程[10]:


图1 车辆运动学模型Fig.1 Vehicle kinematics model
式(1)为非线性连续方程,对其进行离散化处理,离散化周期为T,则可以得到离散化模型:
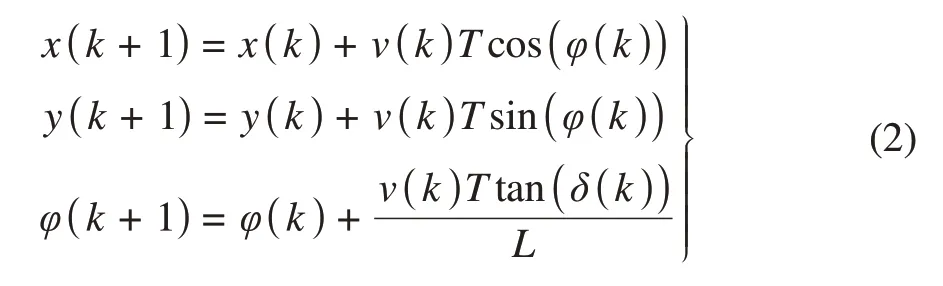
由于转向控制器响应转向指令时存在一定的延迟,转向控制器响应模型可被设计为“一阶惯性环节+纯时滞环节”[7]形式:

式中:δreal(t)——转向控制器反馈的状态值;δdes(t)——转向控制器下发的指令值;τp——一阶惯性时间常数,τp>0;τd——纯滞后时间,τd>0。
若设计横向NMPC模型时考虑转向控制器延迟,则需要对式(1)中状态进行增广[4],但这会极大增加NMPC问题的计算量,甚至可能超出车载无人驾驶系统的运算能力范围。因此,在设计横向NMPC模型时不考虑转向控制器的延迟,但需要对转向控制器的延迟环节进行补偿处理[14]。假设求解横向NMPC控制问题得到的最优车轮转角序列为u*,则设计补偿策略得到的第k时刻最优期望车轮转角为
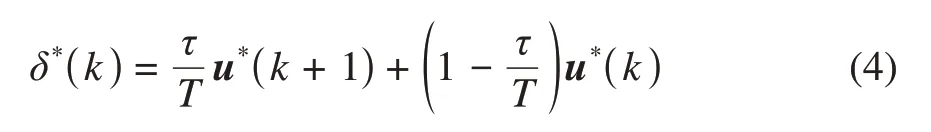
式中:τ——转向控制器延迟时间常数,且满足τ≥τd,τ通过试验数据估计得到。
2 车辆横向NMPC模型
在建立车辆横向运动学模型后,车辆横向NMPC模型的建立过程还包括设计NMPC参考路径点、目标函数及模型约束条件的设计,以及为了提高NMPC求解效率而进行的NMPC初始值设计。
2.1 NMPC参考路径点
假设从路径规划模块获得的一段参考路径点包含(xref(i),yref(i),φref(i),κ(i)),i=1,2,...,M,其中,(xref(i),yref(i))为参考路径点坐标,φref(i)为参考路径点的横摆角,κ(i)为参考路径点曲率,M为参考路径点的序列长度。
根据车辆的当前位姿状态(x(k),y(k),φ(k)),在参考路径上进行遍历搜索,得到的最近点knearest需要满足如下两个条件:
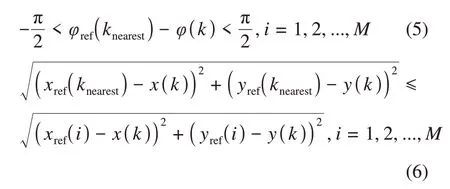
从参考路径的最近点knearest开始,每间隔Δs选取一个预测参考路径点,其中Δs=v(k)T;假设共N个预测参考路径点,即N为NMPC的预测步长,则得到的预测参考路径序列为(xref,mpc(i),yref,mpc(i),φref,mpc(i)),i=1,2,…,N。
2.2 权重自适应目标函数
NMPC控制器的目标是使横向偏差和横摆角偏差最小化,并且保证车轮转向角控制动作平稳,因此构建的NMPC控制器目标函数为

式中:si——横向偏差的权重系数,si≥0;qi——横摆角偏差的权重系数,qi≥0;ri——车轮转角单步增量的权重系数,ri≥0;Δu(k+i)——车轮转角单步增量;ey(k+i)——横向偏差;eφ(k+i)——横 摆 角偏差。
横向偏差ey(k+i)的计算表达式为
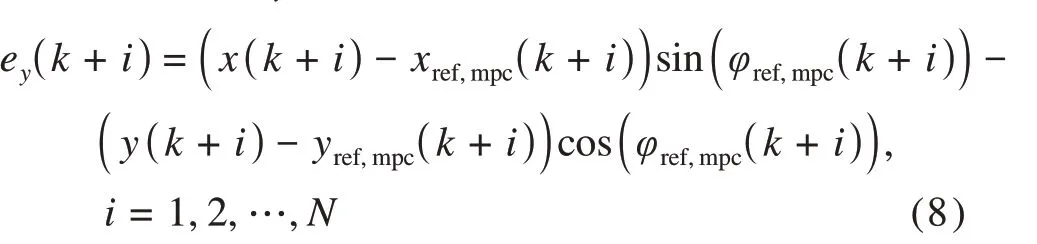
横摆角偏差eφ(k+i)的计算表达式为
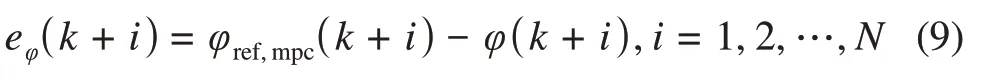
车轮转角单步增量Δu(k+i)的计算表达式为
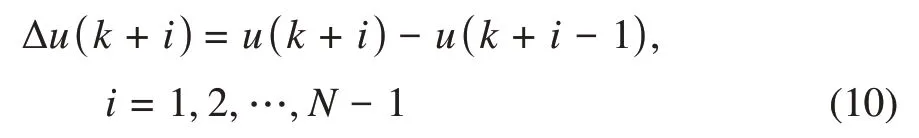
式中:u(k)——车辆前轮转向角,u(k)=δ(k)。
考虑到车辆在行驶过程中速度不断变化,在高速行驶过程中容易发生高速摆动(车辆横摆角左右摆动),在大曲率转弯或者走S形线路时会出现横向偏差和横摆角偏差较大的现象,固定的权重系数很难适应所有的复杂场景,因此本文采用权重系数自适应的策略。所设计自适应权重系数如下:
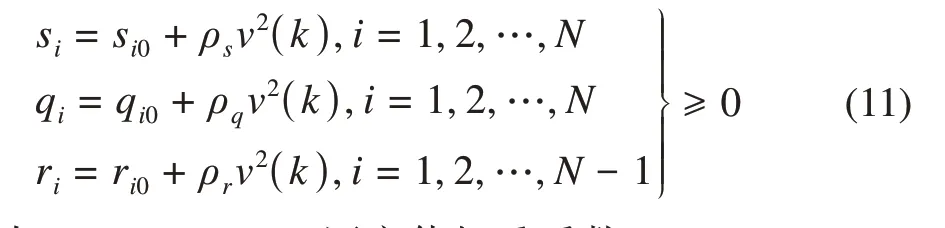
式中:si0,qi0,ri0——固定值权重系数,si0≥0,qi0≥0,ri0≥0;ρs,ρq,ρr——速 度 平 方 权 重 参 数,ρs≥0,ρq≥0,ρr≥0。
2.3 模型约束条件
假设车辆转向器的最大转向角为δmax,最大转向速度为,整车的控制周期为Tc,车辆横向运动学模型的离散化周期T=mTc,m为正整数,需要满足如下最大车轮转角约束:
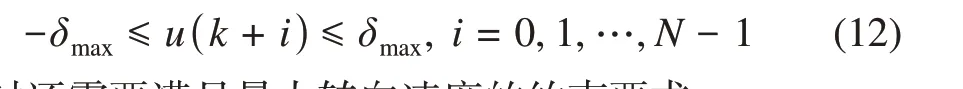
同时还需要满足最大转向速度的约束要求:
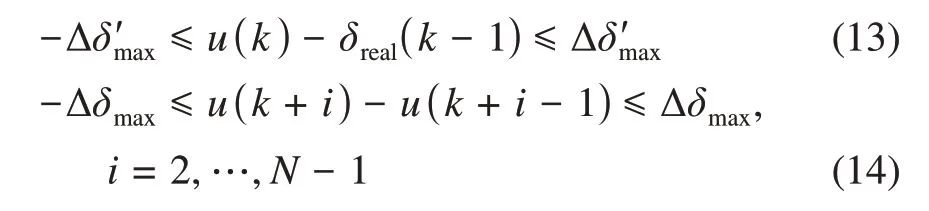
式中:δreal(k-1)——第(k-1)控制时刻车轮转角的实际状态值;Δδ'max——相邻控制周期间车轮转角最大单步增量;Δδmax——相邻模型离散化周期间车轮转角最大单步增量则可以构建目标函数权重自适应的NMPC模型,具体如下:
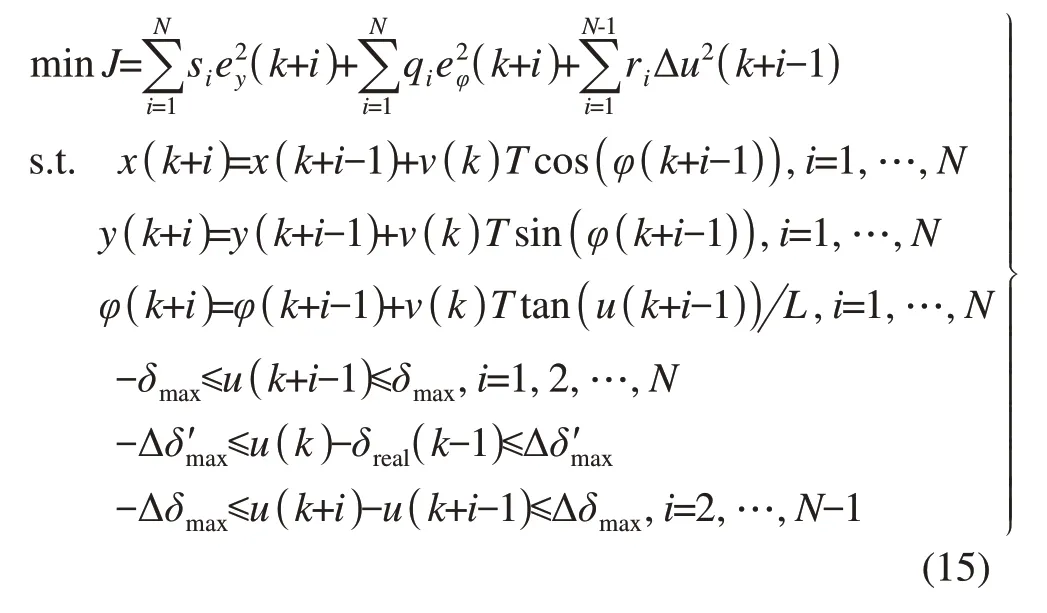
2.4 NMPC初始值
NMPC模型中有4N个优化变量,x(k+1),…,x(k+N),y(k+1),…,y(k+N),φ(k+1),…,φ(k+N),u(k),…,u(k+N-1),求解式(15)时若设置初始值恰当,则可以提高求解效率。在第k时刻,已知车辆的位姿状态(x(k),y(k),φ(k))以及NMPC参考路径信息中路径点曲率κ(i),由κ(i)可以计算路线的参考转向角:

将δref(1),δref(2),…,δref(N)作为车轮转角预测序列的初始值,再依据式(2)进行更新,则可以分别得到车辆横坐标序列初始值x'(k+1),…,x'(k+N),车辆纵坐标序列初始值y'(k+1),…,y'(k+N)以及车辆横摆角序列初始值φ'(k+1),…,φ'(k+N)。
3 实车试验
采用本文提出的NMPC控制策略在神延西湾露天煤矿试验场进行横向控制实车试验。为了测试复杂场景下NMPC的控制效果,分别在30 km/h高速直线线路、大曲率转弯线路、S形线路、倒车线路运行场景下进行实车试验。试验用矿山运输车辆如图2所示,车辆轴长L=6.35 m,转向控制器延迟时间常数τ=0.6 s,最大转向角为δmax=30°,最大转向速度为20()°/s。NMPC求解设置参数如下:离散化周期T=0.1 s,预测步长N=60,权重系数si0=1,ρs=0.1,qi0=0.5,ρq=0.25,ri0=20,ρr=0.9。

图2 矿用卡车Fig.2 Mine truck
在30 km/h高速直线运行时,运行线路的曲率曲线如图3所示,试验结果如图4~图8所示。从图中可以看出,车辆高速直线运行时无频繁摆动现象出现,横摆角偏差在-1.5°至1.2°范围内变化;横向偏差在-0.15 m至0.07 m范围内变化,高速直线运行时的横向控制效果较好;NMPC计算耗时基本上都在单个控制周期(20 ms)以内,个别控制周期有NMPC计算超时的现象。
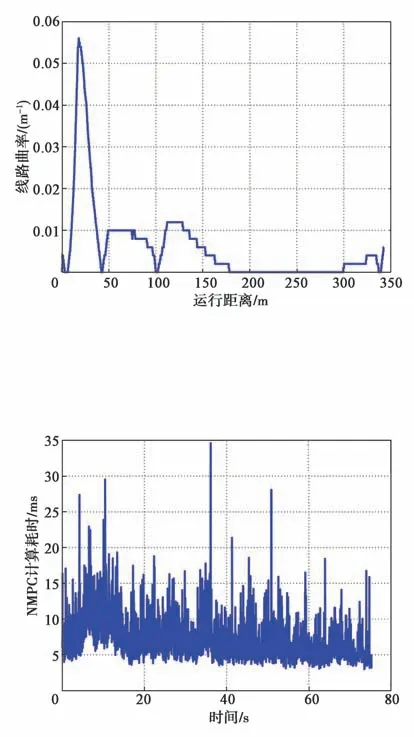
图3 线路曲率曲线(车速为30 km/h)Fig.3 Line curvature curve with the speed of 30 km/h

图4 NMPC计算耗时曲线(车速为30 km/h)Fig.4 NMPC calculation time-consuming curve with the speed of 30 km/h
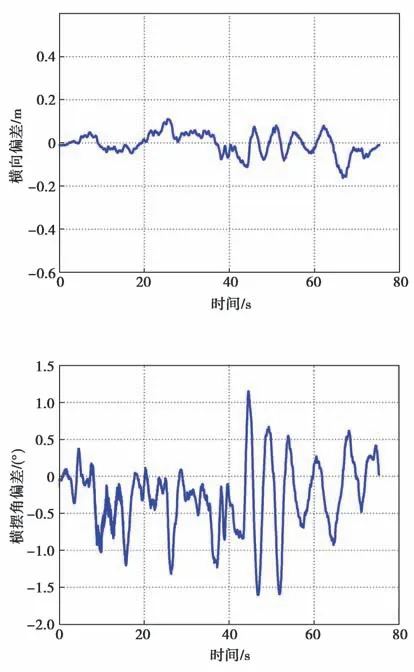
图8 横摆角偏差曲线(车速为30 km/h)Fig.8 Yaw angle error curve with the speed of 30 km/h
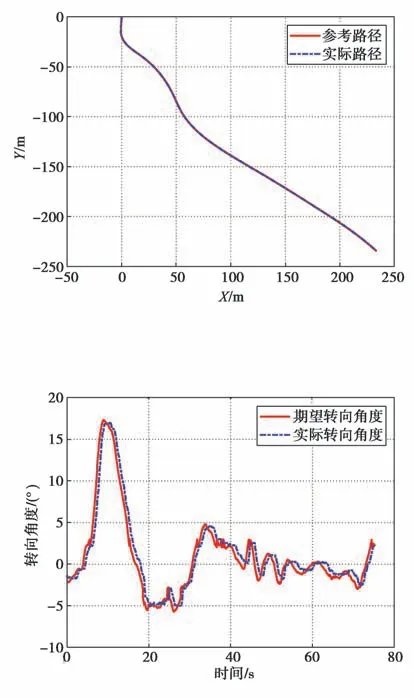
图5 运行轨迹曲线(车速为30 km/h)Fig.5 Running track curve with the speed of 30 km/h
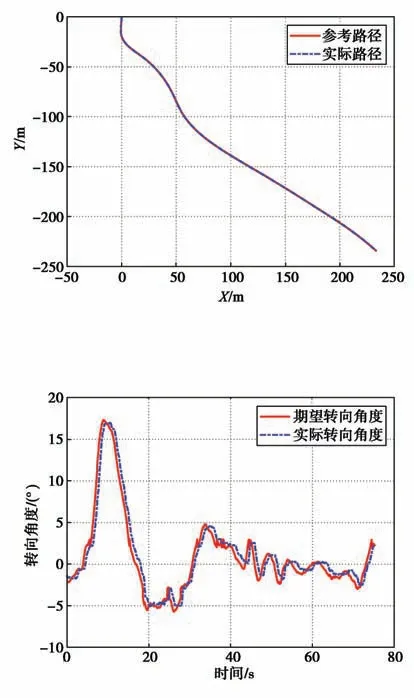
图6 车轮转角曲线(车速为30 km/h)Fig.6 Wheel angle curve with the speed of 30 km/h

图7 横向偏差曲线(车速为30 km/h)Fig.7 Lateral error curve with the speed of 30 km/h
在15 km/h大曲率转弯运行时,运行线路的曲率曲线如图9所示,试验结果如图10~图14所示。从图中可以看出,大曲率转弯运行时无偏差过大现象,横摆角偏差在-4°至3.5°之间变化,横向偏差在-0.22 m至0.09 m之间变化,大曲率转弯运行时的横向控制效果较好,NMPC计算耗时基本上都在单个控制周期20 ms以内,个别控制周期有NMPC计算超时的现象。
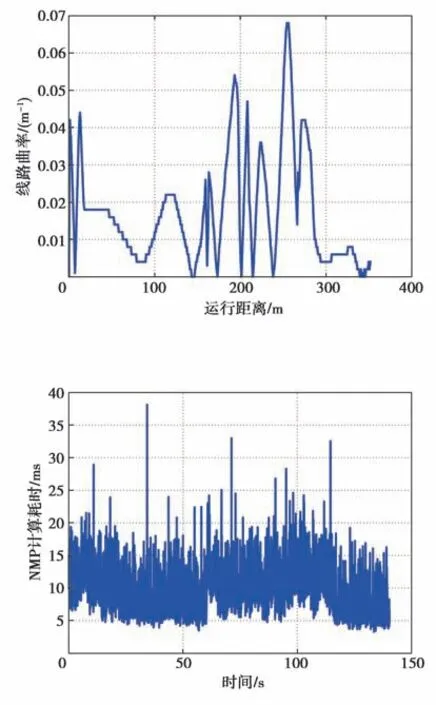
图9 线路曲率曲线(车速为15 km/h)Fig.9 Line curvature curve with the speed of 15 km/h

图10 NMPC计算耗时曲线(车速为15 km/h)Fig.10 NMPC calculation time-consuming curve with the speed of 15 km/h
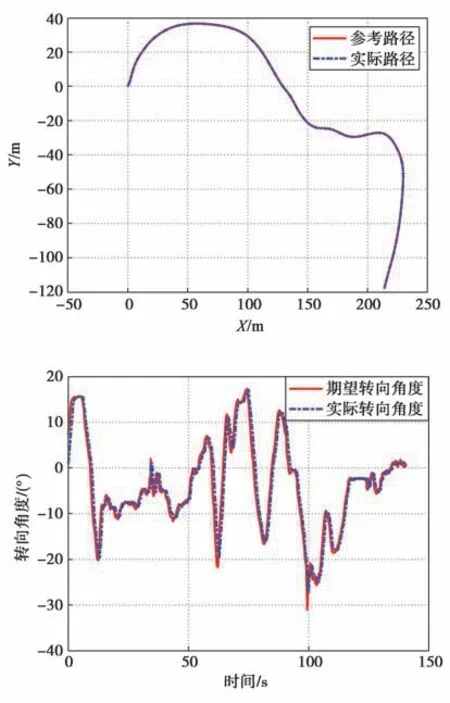
图11 运行轨迹曲线(车速为15 km/h)Fig.11 Running track curve with the speed of 15 km/h
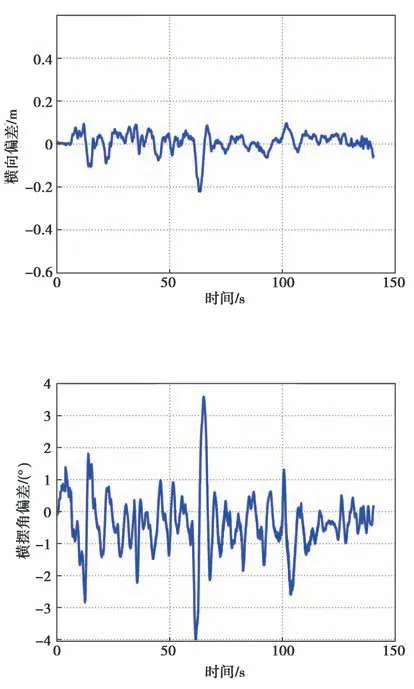
图14 横摆角偏差曲线(车速为15 km/h)Fig.14 Yaw angle error curve with the speed of 15 km/h

图12 车轮转角曲线(车速为15 km/h)Fig.12 Wheel angle curve with the speed of 15 km/h

图13 横向偏差曲线(车速为15 km/h)Fig.13 Lateral error curve with the speed of 15 km/h
在25 km/h的S形线路运行时,运行线路的曲率曲线如图15所示,试验结果如图16~图20所示。从图中可以看出,S形线路运行时无偏差过大现象,横摆角偏差在-2°至1.2°之间变化,横向偏差在-0.12 m至0.15 m之间变化,S形线路运行时的横向控制效果较好,NMPC计算耗时基本上都在单个控制周期20 ms以内,个别控制周期有NMPC计算超时的现象。
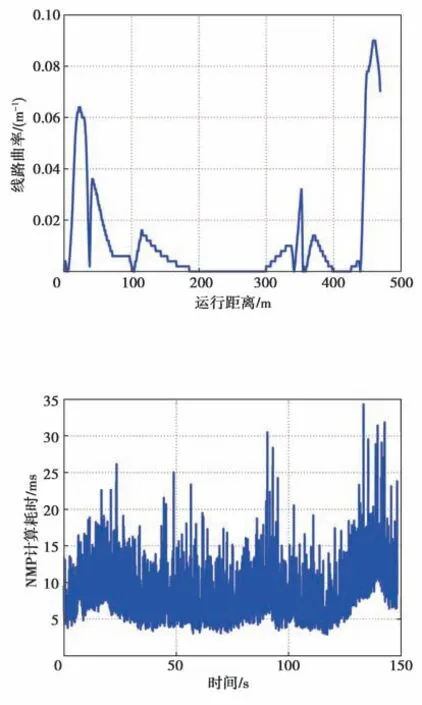
图15 线路曲率曲线(车速为25 km/h)Fig.15 Line curvature curve with the speed of 25 km/h

图16 NMPC计算耗时曲线(车速为25 km/h)Fig.16 NMPC calculation time-consuming curve with the speed of 25 km/h
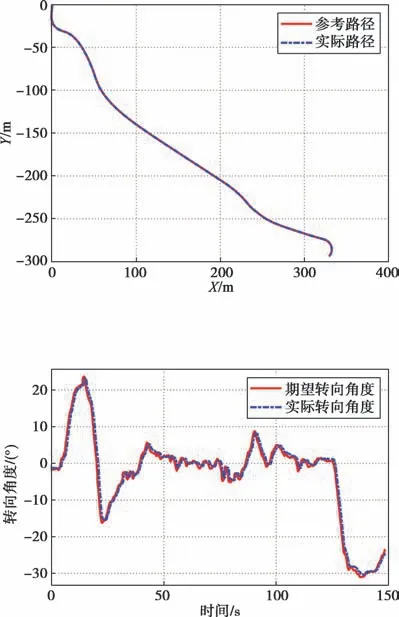
图17 运行轨迹曲线(车速为25 km/h)Fig.17 Running track curve with the speed of 25 km/h

图18 车轮转角曲线(车速为25 km/h)Fig.18 Wheel angle curve with the speed of 25 km/h
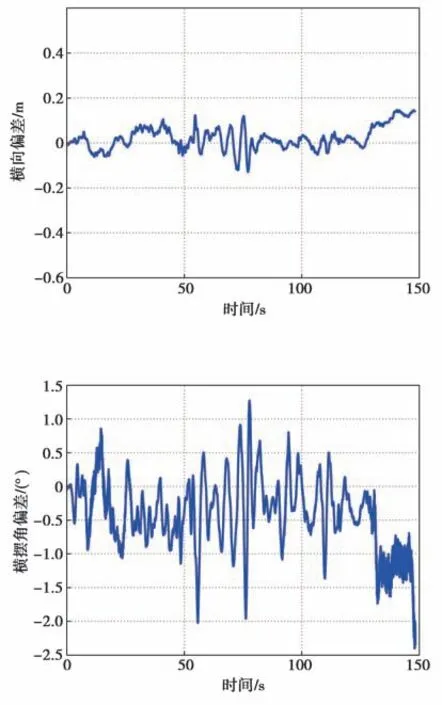
图20 横摆角偏差曲线(车速为25 km/h)Fig.20 Yaw angle error curve with the speed of 25 km/h

图19 横向偏差曲线(车速为25 km/h)Fig.19 Lateral error curve with the speed of 25 km/h
在6 km/h的倒车线路运行时,运行线路的曲率曲线如图21所示,试验结果如图22~图26所示。从图中可以看出,倒车运行时无偏差过大现象,横摆角偏差在-1.7°至2.2°之 间 变 化,横 向 偏 差在-0.07 m至0.09 m之间变化,倒车运行时的横向控制效果较好,NMPC计算耗时基本上都在单个控制周期20 ms以内,只出现1次控制周期NMPC计算超时的现象。
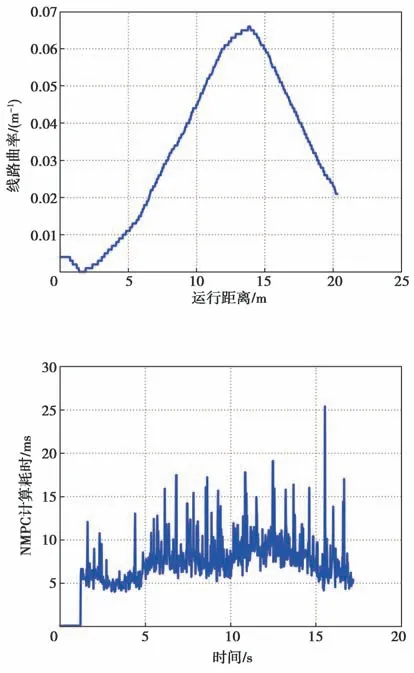
图21 线路曲率曲线(车速为6 km/h)Fig.21 Line curvature curve with the speed of 6 km/h

图22 NMPC计算耗时曲线(车速为6 km/h)Fig.22 NMPC calculation time-consuming curve with the speed of 6 km/h
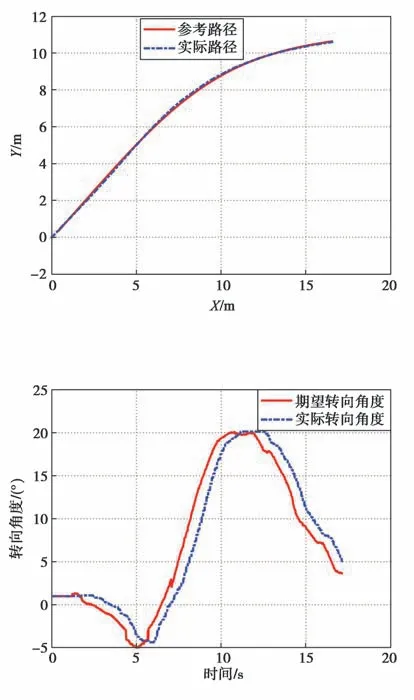
图23 运行轨迹曲线(车速为6 km/h)Fig.23 Running track curve with the speed of 6 km/h

图24 车轮转角曲线(车速为6 km/h)Fig.24 Wheel angle curve with the speed of 6 km/h
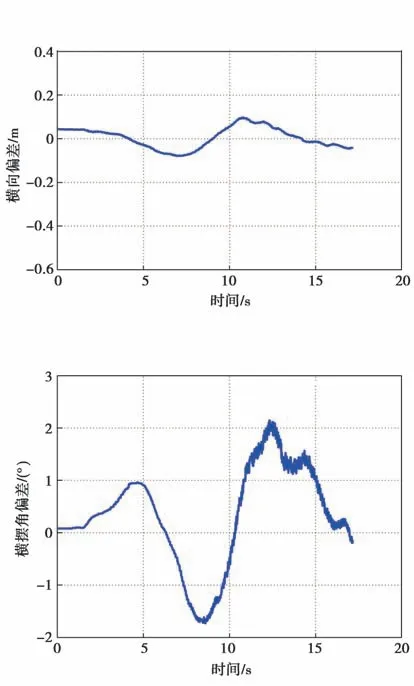
图25 横向偏差曲(车速为6 km/h)Fig.25 Lateral error curve with the speed of 6 km/h

图26 横摆角偏差曲线(车速为6 km/h)Fig.26 Yaw angle error curve with the speed of 6 km/h
4 结语
针对矿山运输车辆在矿区运行过程中的高速直线行驶、大曲率转弯、走S形线路等复杂多变场景时容易出现高速摆动、横向偏差和横摆角偏差较大的现象,本文设计了一种目标函数权重自适应的NMPC控制策略。其针对转向控制器存在延迟的情况,建立了转向控制器的“一阶惯性环节+纯时滞环节”的转向延迟模型。考虑到车载无人驾驶系统的运算能力,在建立NMPC模型时不考虑转向延迟模型,而在NMPC计算得到最优车轮转角序列时设计转向延迟的补偿策略。最后通过矿山运输车辆实车试验验证了所提方法的可行性。但在实车试验中发现有个别控制周期出现NMPC计算超时现象,因此,后续将研发适用于NMPC求解的高效优化求解器。

