基于优化控制的矿山狭窄通道车辆轨迹规划方法
林雪容,谢和平,2,徐 彪,3,袁诗杰,边有钢,3,胡满江,3,秦兆博,3,胡家喜
(1.湖南大学 机械与运载工程学院,湖南 长沙4 10082;2.徐州徐工矿业机械有限公司,江苏 徐州 210009;3.湖南大学 无锡智能控制研究院,江苏 无锡 214115;4.株洲中车时代电气股份有限公司,湖南 株洲 412001)
0 引言
近年来,智能车辆技术已在矿山、港口、园区等场景实现示范应用,有望大幅提升矿山开采运输作业效率和安全。轨迹规划技术作为智能车辆的核心技术之一,旨在规划出连接车辆始末位姿且安全可执行的轨迹[1],得到了广泛的关注和研究。
目前,关于轨迹规划问题的研究方法主要可以分为4类:曲线插值法、随机采样法、图搜索法以及数值优化法[2]。曲线插值法通过采用曲线插值预设的路点生成轨迹,常见的插值曲线有RS曲线、螺旋曲线、贝塞尔曲线以及样条曲线[3]等。随机采样法则在车辆运动构型空间中采样路径节点以找到连接车辆始末位姿的轨迹[4]。曲线插值法和随机采样法虽然都较为容易实现,但在复杂作业场景下,却常常不可行。具体表现为曲线插值法深受预设路点影响,而随机采样法生成的轨迹曲率不连续,且它们所生成的轨迹都是次优解[5]。图搜索方法能通过遍历状态空间的最小代价路径而找到最优解[6],但其在高维空间中搜索效率低。因此,有学者提出图搜索与曲线插值或随机采样的组合方法[7-8]。这样尽管能够搜索出最优解,但也不能直接处理如障碍物碰撞、车辆执行机构限值等复杂约束。数值优化法通过构造精确的数学模型来生成最优轨迹,它能以数学描述的形式处理轨迹规划问题,包括其中的各种复杂约束[9]。数值优化法生成的轨迹安全可执行且连续平滑,但它存在计算复杂的缺陷[10]。可见,尽管现存研究方法多种多样,轨迹规划问题仍具有相当的挑战性,尤其是复杂环境下的轨迹规划。例如,狭窄通道就是一种典型的复杂环境,其在露天矿山等场景中广泛存在。因受通道左右边界的严格限制,在这样的环境中,车辆自由空间相当狭小,生成安全可执行的通行轨迹是很困难的[11]。现存关于狭窄区域轨迹规划的研究对象主要为轮式机器人,常用的规划方法为随机采样法[12]。然而,不同于轮式机器人能够原地转向的特性,受非完整约束限制的智能车辆显然不能在狭窄环境中应用随机采样法生成曲率不连续的轨迹。考虑到数值优化方法能通过数学建模处理复杂约束的特点,本文针对矿山狭窄通道轨迹规划提出一种基于优化控制的轨迹规划方法,目的是希望轨迹规划生成的轨迹满足跟踪控制要求,以提升轨迹跟踪控制效果。
1 问题描述
由于通道是否狭窄为一个相对的概念,本文定义狭窄通道场景为车身宽度占比超过通道宽度的二分之一且仅允许单车单向行驶。在这样的场景中,车辆运行环境单一、固定,因此其轨迹规划的任务需求可以为离线生成连接通道进出口、安全无碰撞、可多次重复使用的全局运动轨迹X。
1.1 狭窄通道环境分析
狭窄通道中,车辆运动被通道边界限制在非常有限的空间内,这对计划经过该通道的车辆而言,会面临两大难点。首先,车辆轨迹如何保持全程与通道边界无碰撞;其次,车辆轨迹如何变化才能保证车辆顺利地通过转弯拐角。这无疑对轨迹规划提出了相当高的要求。这两个难点是狭窄通道场景的重要属性,也是本文要解决的问题。
1.2 狭窄通道环境模型
如上所述,狭窄通道中车辆通行的两大难题是避免边界碰撞和如何通过空间相当狭小的拐角,因此,狭窄通道的环境模型应着重体现边界与拐角。图1示出狭窄通道模型示意。图中,Ai,l,Bi,l,Ci,l为第i段通道左边界直线参数;Ai,r,Bi,r,Ci,r为第i段通道右边界参数;如图1所示,l1,l与l1,r分别表示通道第1段的左右边界直线;若驾驶通道由Ns段组成,则i从1变化至Ns。本文将狭窄通道环境的原始边界内缩,构建由若干管状路段组成的驾驶通道模型。这样不仅明确了驾驶通道边界,同时还预留出一定的安全空间。显然,该驾驶通道模型由其左右边界确定,而其左右边界具体描述如下:


图1 狭窄通道模型示意图Fig.1 Schematic diagram of narrow corridor model
2 狭窄通道轨迹规划建模方法
本节在图1所示狭窄通道环境模型的基础上,从车辆模型出发,分析车辆运动轨迹优化目标以及轨迹始末状态约束、车辆运动学约束、边界碰撞约束和车辆可执行性约束等,构造轨迹规划优化控制模型,求解该模型得到的优化控制序列再经,最后由车辆系统模型积分,得到初始优化轨迹,如图2所示。

图2 车辆运动学模型示意图Fig.2 Schematic diagram of vehicle kinematics model
2.1 轨迹规划的车辆模型
为保证安全通行,狭窄通道中车辆运行速度较低,因此,本文采用车辆运动学模型作为轨迹规划的车辆模型,该模型满足阿克曼转角定理[13]。
若用车轮后轴坐标中心表示车辆位置,车辆运动学模型的数学描述如下:

式中:(x,y)——车辆后轴中心坐标。
2.2 狭窄通道空间近似离散策略
轨迹规划中通常以离散轨迹序列点来描述轨迹,轨迹既可在时域离散为X(t(k)),又可在空间域离散为X(s(k)),如图3所示。

图3 轨迹离散示意图Fig.3 Schematic diagram of trajectory discretization
当前轨迹规划问题中,不管是时间离散还是空间离散,其离散间隔都是未知的。因狭窄通道车辆自由空间狭小,在自由空间中连接车辆始末位姿的路径总长整体差距小,将这些路径以相同数目离散,则其离散间隔会几乎相同。由此,本文针对狭窄通道轨迹规划,提出一种空间近似离散策略,即将总长确定的狭窄通道模型的通道中心线进行离散,并以其离散间隔近似代替目标轨迹的离散间隔。式(6)~式(10)为将目标轨迹离散为N个状态点后,基于优化控制的轨迹规划模型在空间域离散的数学描述。若将已知通道中心线离散,用离散点sc(k)近似代替未知目标轨迹离散点s(k),显然,该模型能够得到很大简化。
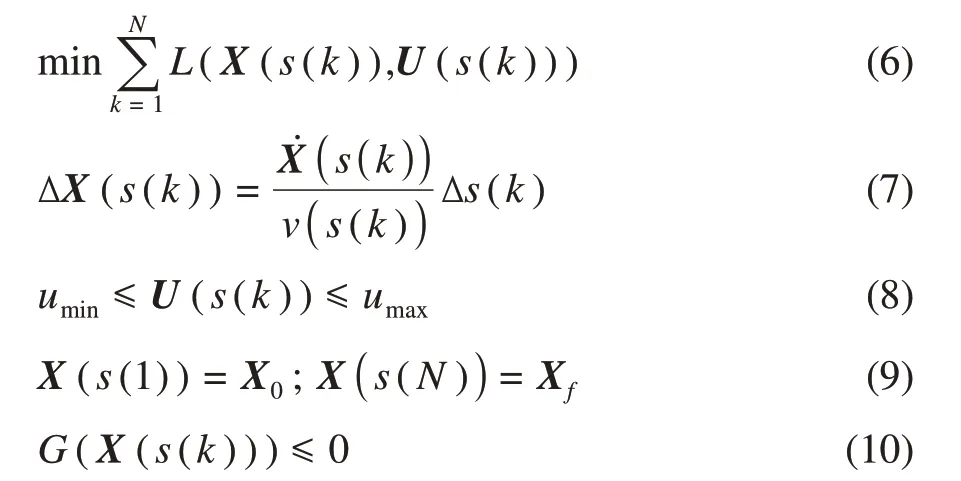
式中:umin——控制向量的下界;U(s(k))——离散点k处的控制向量;X(s(k))——离散点k处的状态向量;X0和Xf——轨迹起止点的状态向量;umax——控制向量的上界;G(X(s(k)))——除控制量约束外的其他约束。
针对通道中心线的离散规则,考虑到拐角处车辆运行条件更为严苛,因此将狭窄通道划为通道直行段与通道拐角段;并在均匀离散直行段的基础上,以更小的间距均匀离散拐角段,便于后续优化模型求解。如图4所示,直行段与拐角段由通道转弯中心与转弯半径唯一确定。
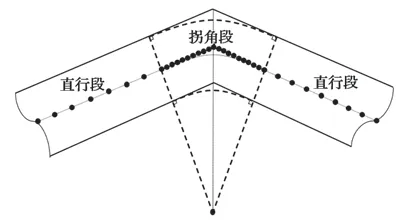
图4 狭窄通道中心线离散示意图Fig.4 Schematic diagram of narrow corridor centerline discretization
2.3 狭窄通道轨迹规划优化控制模型
基于上述空间近似离散策略,将车辆目标轨迹X离散为轨迹序列点ζ,则目标轨迹序列点满足式(11)和式(12)要求。

基于优化控制来保证轨迹安全可执行且曲率连续,兼顾轨迹通行效率,轨迹规划模型构造包括目标函数建模和约束条件建模。
2.3.1 目标函数建模
为满足车辆通行狭窄通道的高效性,本文以通行时间为代价,构造目标函数。基于上文的空间近似离散策略,狭窄通道的通行时间可近似表达为

式中:Δsc(k+1)——相邻离散点之间的距离,Δsc(k+1)=sc(k+1)-sc(k);v(k)——在k点处的行驶速度。
2.3.2 约束条件建模
轨迹规划需要考虑的约束条件为碰撞躲避约束、车辆运动学约束、平滑舒适性约束。
首先,考虑到所规划的轨迹需要能够被车辆有效跟踪,故建立车辆运动学约束。基于空间近似离散策略,车辆运动学约束可近似表达为
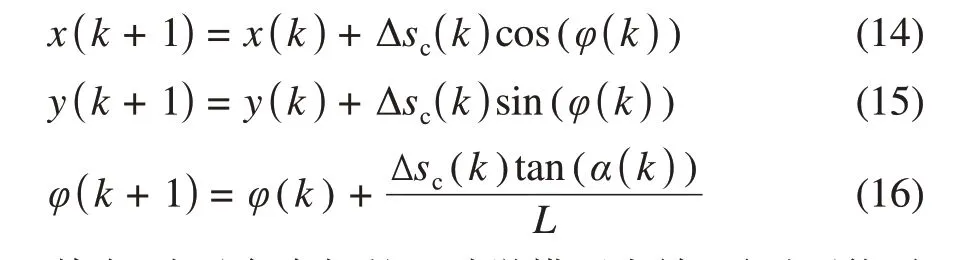
其次,为避免车辆的运动学模型失效,需对可能引起车轮侧偏角过大的侧向加速度施加约束。综合阿克曼转角定理,车辆的转弯半径R与车轮转角α和车轮轴距L的关系为,可建立如下约束不等式:

式中:μ——侧偏力系数;g——重力加速度系数。
第三,轨迹的初始位姿应与车辆初始位姿一致,车辆目标位姿应与轨迹终止位姿一致。终止位置位于通道中心线末端,横摆角与通道航向角对齐一致,则轨迹始末位姿约束如下:

式中:(xc(N),yc(N))——通道中心线末端位置;θc(N)——通道中心线末端朝向。
第四,需考虑车辆控制执行机构工作范围。车辆控制包括横向控制与纵向控制。一方面,狭窄通道中,为保证车辆顺利转弯,其横向控制极有可能达到执行机构的工作限值,故横向控制执行机构工作范围的约束不可忽略。另一方面,狭窄通道中,车辆运行速度低,其纵向控制远不会到达纵向控制执行机构的工作极限。横向控制执行机构工作范围包括两方面:一是前轮转角,二是前轮转角角速度。对二者添加如下约束:

为保证运行舒适性,本文对纵向控制同样进行约束,即设定速度与加速度满足如下关系:

最后,也是最重要的,为保证安全性,在狭窄通道中,须考虑车辆与边界的碰撞可能性,由此设置避障约束。对于车辆与边界的防碰撞处理,如图5所示,本文采用圆拟合方式表示车辆外轮廓,以预留出安全空间。对车长方向的两条车身边界线进行Nc等分,根据四点共圆定理,获得Nc个半径为r的圆。其分别以车宽w和车长l的Nc等分长为直角边,通过勾股定理计算得到圆的直径,随后乘以系数0.5获得半径。拟合圆参数满足式(25)~式(27)。

图5 圆拟合示意图Fig.5 Schematic diagram of circle fitting strategy

式中:(xj,ο(k),yj,ο(k))——第j个拟合圆的圆心位置,j=1,2,…,NC;lf——车辆前悬距。
结合由若干管状段组合成的狭窄通道环境模型可发现,只要维持拟合圆圆心到边界距离大于拟合圆的半径,即可保证车辆与边界无碰撞发生,如图6所示。

图6 避障约束条件示意图Fig.6 Schematic diagram of collision avoidance
其中,圆心到边界距离满足式(28)和式(29)要求:
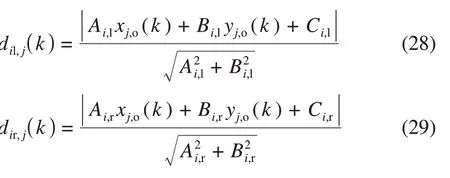
式中:dil,j(k)、dir,j(k)——第j个拟合圆圆心到第i段通道左、右边界的距离。
拟合圆圆心到通道边界的距离需大于车身拟合圆的半径r,即为避免车辆与边界碰撞,须保证式(30)和式(31)成立。
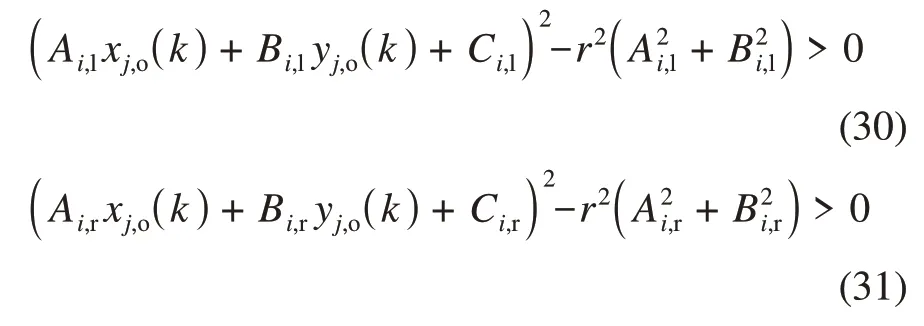
3 轨迹平滑后处理
在上述优化问题求得解之后,还需要对所生成的轨迹进行优化,以满足车辆行驶的平顺性、舒适性等要求。本文基于二次规划来平滑轨迹规划模型生成的初始优化轨迹。为满足生成轨迹曲率波动小、速度平滑等要求,二次规划的优化项主要包括两方面:一是平滑后相邻两个轨迹状态点变化之差;二是平滑后的轨迹点与初始优化轨迹点之间的误差。最终,优化目标函数表达式如下:
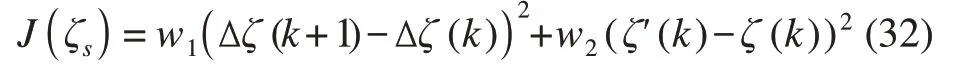
式中:ζ(k)和ζ'(k)——轨迹优化前后第k个状态点,ζ(k)=[x(k),y(k),φ(k),v(k)],k=1,2,…,N-1;Δζ(k)——状态点k优化前后的状态变化,Δζ(k)=ζ'(k)-ζ(k);w1,w2——权重系数。
在求解二次规划问题时,需要将其化简为标准形式。将式(32)化简,可获得如式(33)所示的求解标准式。

在平滑处理后,轨迹点信息包含位置、速度、航向角,这些信息将被输送给控制模块来实现车辆的跟踪控制。
4 仿真验证
本文2.3节中所提出的轨迹规划优化控制模型为非线性优化模型,可采用内点法进行求解。本节通过仿真对比实验来验证本文方法的可行性及其相较参照方法的优势。首先,基于Matlab设计若干组狭窄通道场景;然后,分别采用本文方法与参照方法生成对应场景的轨迹;最后根据评价指标比较本文方法与参考方法的轨迹生成能力与生成轨迹的质量[14]。
4.1 参照方法的选取
轨迹规划方法主要可分为基于图搜索、基于采样、基于插值曲线以及数值优化。基于采样的方法以RRT方法为代表,但它由于算法难以收敛、计算时间长等因素,不适用于狭窄通道。基于插值曲线的方法仅适用于城市化道路,如高速公路等场景。混合A*算法是一类经典的图搜索类算法,其能在环境地图中找到连接始末位姿而且满足车辆非完整约束的最优路径[15],因而被广泛应用于复杂场景路径规划。所以,本文引入混合A*算法作为参照方法。由于轨迹规划包括路径与速度规划,除了混合A*算法规划路径外,本文还引入非线性规划作为参照方法的速度规划方法,以保证车辆模型的有效性。在混合A*算法中,路径生成的实现方式是在满足车辆运动学的状态空间中拓展最小代价的栅格地图节点。由于拓展节点受栅格精度影响,有可能永远不能达到目标状态,为此,需设置终止条件,即当扩展节点达到目标状态的某邻域时搜索结束。本文仿真设置该 邻域范围为:Δx=±0.25 m,Δy=±0.25 m,Δφ=±15°。
4.2 对比实验设计
轨迹规划方法评价包括轨迹生成能力评价与生成轨迹质量评价。本文从如下3点来评价本文方法与参照方法:(1)可行解下的狭窄通道拐角极限;(2)求解效率;(3)曲率和加速度变化幅度。其中,前两点用于评价轨迹生成能力,最后一点用于评价生成轨迹的质量。
根据上文,狭窄通道车辆运行的两个难点分别体现在边界碰撞与拐角通行上,故本文仿真实验设计带有拐角的狭窄通道。图7为仿真场景示意,其中T表示通道拐角。针对两种方法可行解的拐角极限值探索,本文设计T从180°开始按5°差值依次递减,直到各方法不能找到可行解。对其他2个仿真评价点,本文在两种方法能搜到可行解的范围内,取4组不同T值对应的通道,比较在这4组通道中两种方法所生成轨迹的运动参数与跟踪控制效果。狭窄通道的参数设置主要为通道宽度与通道拐角。本文设置通道宽度为3.5 m,拐角未定。

图7 仿真实验狭窄通道设计示意Fig.7 Schematic diagram of narrow corridor design in the simulation test
仿真实验参数除了通道参数,还包括车辆几何参数、车辆执行机构工作范围、车辆运动参数的限值、车辆侧向力系数和车辆重力加速度系数。本文以林肯MKZ作为参照车辆模型,其具体参数设置见表1。
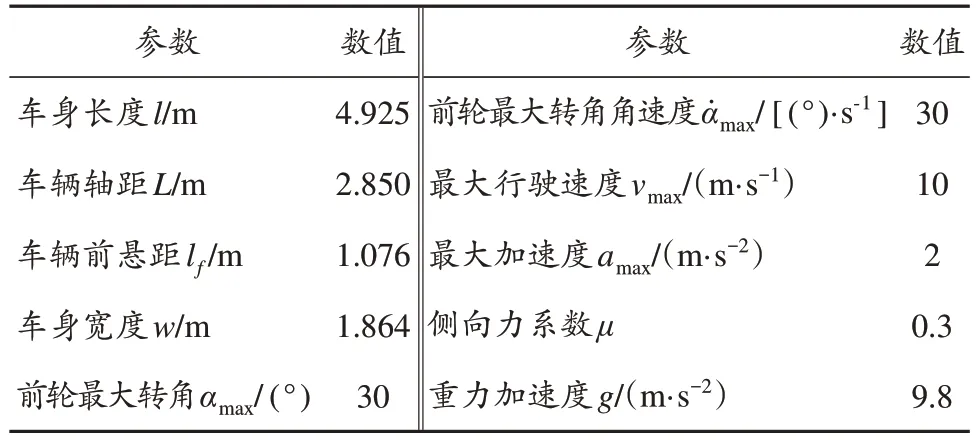
表1 狭窄通道车辆轨迹规划仿真实验车辆参数设置Tab.1 Parameter setting of the simulation test for vehicle trajectory planning in narrow corridor
4.3 仿真实验结果
本节按照4.2节的实验参数进行仿真实验,并分别从性能指标和轨迹图的角度对实验结果进行了分析。
4.3.1 性能指标分析
实验结果如表2所示。经实验验证,当拐角T从180°起按5°依次递减,本文方法能找到可行解的最小拐角为120°,而参照方法为130°,因此,本文方法相较参照方法适用范围更广。随后,分别取拐角T为180°,165°,150°,135°的4组狭窄通道,对其进行轨迹规划,并将4组通道轨迹求解的平均时间、平均最大曲率和平均通行时间分别记录于表2。从表2可知,参照方法的求解效率明显低于本文所提方法的,这是因为狭窄通道场景对参照方法栅格精度要求大大提升,以致其求解时间指数式增长。在狭窄场景下,车辆运行路线单一,且常常是单车通行,因而只需考虑静态障碍物。因此,在实际应用中,采用本文方法可进行离线计算,生成全局轨迹参考。对比两种方法生成的轨迹,参照方法的最大曲率高于本文所提方法的;受曲率与速度制约关系的约束,参照方法的通行效率低于本文方法的。
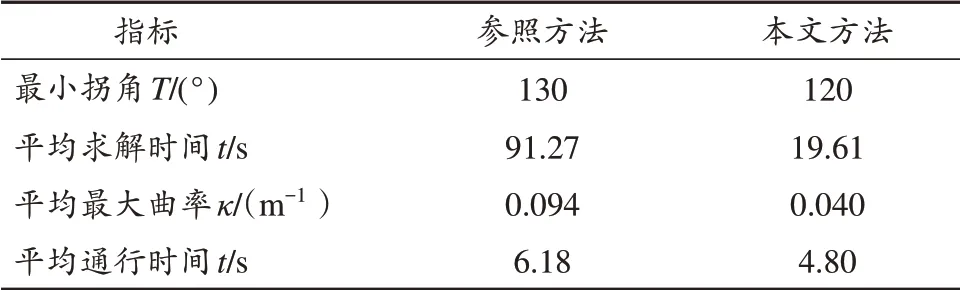
表2 狭窄通道车辆轨迹规划仿真实验性能指标Tab.2 Performance indexes of the simulation test for vehicle trajectory planning in narrow corridor
综上所述,本文所提方法相对于参照方法具有以下优点:(1)适用范围更广;(2)求解效率更高;(3)所生成轨迹曲率更小,通行效率更高。
4.3.2 轨迹图分析
图8为所选4组通道生成轨迹的直观结果。通过比较图8(a)与图8(b)可知,本文方法生成轨迹的行驶速度明显高于参照方法的。通过图8(c)和图8(d)可知,本文方法规划轨迹的加速度变化和曲率变化明显小于参照方法的。本文以混合A*算法作为参照方法,通过离散化前轮转向角进行节点扩展,根据启发函数和代价函数进行节点选择。由于启发函数难以估计当前节点到终止节点的距离,所以在直行道路上其可能选择一些前轮转向角较大的节点,从而导致生成路径的曲率变化较大。故在165°和150°拐角下,参照方法生成的轨迹后端有明显弯曲。由图8(c)可知,在135°和165°拐角下,参照方法在轨迹末端曲率变化较大,所以需要减速以保障车辆行驶安全。
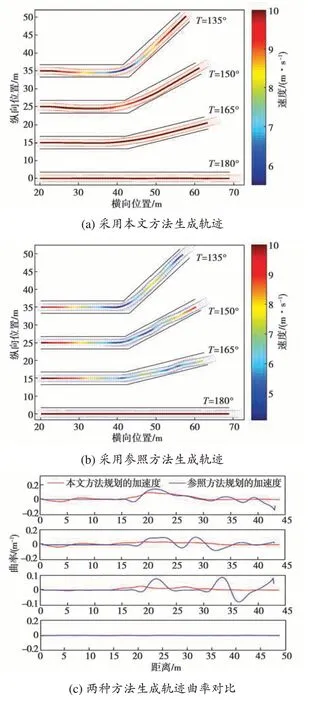
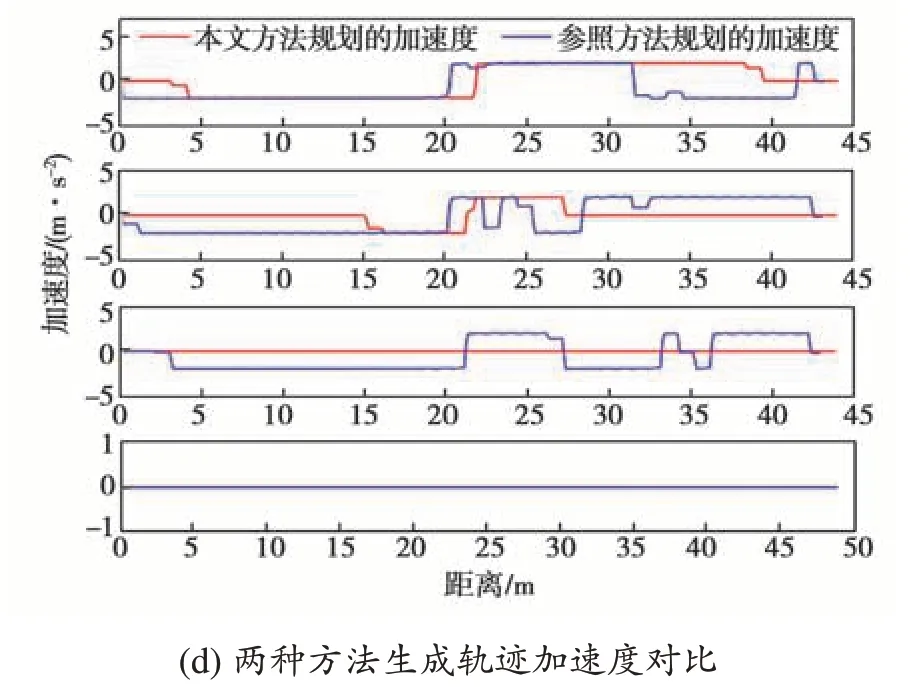
图8 采用两种方法生成的轨迹对比Fig.8 Comparison of the trajectories generated by two methods
综上所述,与参照方法相比,本文方法生成的轨迹平滑性更好、通行效率更高、曲率变化和加速度变化也更加平缓。因此,本文方法所生成轨迹的舒适性更好,轨迹质量更高。
5 结语
本文考虑矿山狭窄通道的场景,针对车辆易与边界发生碰撞及拐角通行困难问题,提出基于优化控制的轨迹规划方法。其首先构建环境模型,再从车辆运动学模型出发,分析车辆的始末状态、执行控制工作范围及边界碰撞条件等约束;然后,基于通道特征提出一种空间近似离散策略,由此构建狭窄通道基于优化控制的轨迹规划模型;最后,对该模型生成的初始优化轨迹,采用二次规划作平滑处理。仿真实验表明,本文所提方法有效可行,与混合A*算法相比,其不同狭窄通道场景下的平均求解时间降低78.5%,平均最大曲率降低57.4%,平均通行时间降低22.3%。因此,在狭窄通道轨迹规划中,相较混合A*方法,本文方法具有适应性更广、求解速度更快的特点,且采用本文方法所生成的轨迹更为连续、平滑。

