钢筋混凝土梁火灾损伤的多元信息融合模型

魏国海,刘才玮,曹永升,刘朝峰,张天亮,修杨

（1. 青岛理工大学 土木工程学院，山东 青岛 266033；2. 河北工业大学 土木与交通学院，天津 300401）

在火灾作用下，钢筋混凝土构件材料性能会有所下降，不仅导致构件的承载力和刚度降低，而且导致动力特性的衰减。由于单一信息源的不确定性，难以全面准确评估混凝土结构的损伤程度，建立钢筋混凝土结构火灾损伤的多元信息融合综合评估方法具有重要意义。

目前，对于火灾后建(构)筑物的评估和修复研究较少，《火灾后建筑结构鉴定标准》(CECS 252—2009)[1]是中国现行推荐标准，其通过外观现象确定损伤等级，考虑因素较为单一，模糊性较大，误差也会偏大。刘才玮等[2]根据火灾后的承载能力、基频、刚度和火灾时间等参数，建立了一套简单的损伤评估体系。Wang等[3]分析了排序反转现象的原因，提出了一种保持局部优先级不变的方法，以避免排序反转现象。Gao等[4]选取混凝土表面颜色、剥落、裂缝和锤击响应作为高温后混凝土损伤的综合评价指标，建立相应的评价标准，提供了一种高温后结构损伤评判的新方法。Miano等[5]提出了一种基于概率的钢筋混凝土结构在地震和火灾作用下的性能评估方法，通过获得不同记录/温度影响下的脆性曲线对所研究的钢筋混凝土结构进行评估。杜国强等[6]在分析影响装配式钢筋混凝土厂房质量因素的基础上，建立了装配式钢筋混凝土厂房质量的层次指标体系，并采用综合赋权方法对各指标进行赋权，建立了装配式厂房质量评价模型。Silla等[7]建立事故模型分析了芬兰1959年—2008年的铁路安全水平，处理方法较为简单，在事故预防方法上因面过于宽而无重点，缺乏预防类似事故发生的具体建议。郭艳飞等[8]采用层次分析法并结合专家经验确定指标权重。综上所述，多元信息融合方法能够准确、全面地评价结构损伤的真实状态。

笔者通过10根钢筋混凝土T形梁的火灾试验、振动测试、静载试验以及数值仿真，建立一套基于多元信息融合的钢筋混凝土梁(RC梁)火灾后损伤评估体系，对10根RC梁进行火灾损伤评估，并与规范方法进行对比，验证评估方法的可靠性，为火灾后混凝土结构的损伤评估提供可靠依据。

1 RC梁火灾试验与数值模拟分析

1.1 火灾—振动试验

试验设计了10根钢筋混凝土T形梁，试件混凝土强度等级为C35，钢筋强度等级均为HRB400，其中1根为未受火的混凝土梁构件，只进行静载试验，其余9根先进行热力耦合试验，然后进行静载试验。试验梁分组见表1，试验梁尺寸及配筋情况见图1，火灾试验布置示意图见图2，部分现场图见图3。

表1 试验分组情况Table 1 Test grouping

图1 T形梁尺寸配筋及热电偶、应变片布置示意图（单位：mm）Fig. 1 Schematic diagram of reinforcement, thermocouple and strain gauge arrangement of T-beam (Unit: mm)

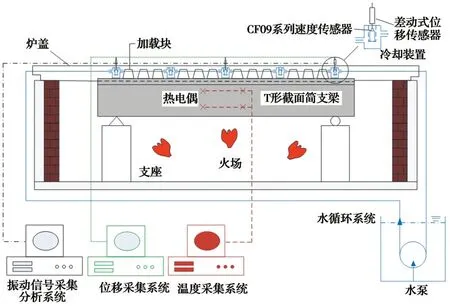
图2 火灾试验布置示意图Fig. 2 Schematic diagram of fire test layout

图3 火灾试验现场图Fig. 3 Fire test site drawing

在火灾试验过程中，测量了试验梁的挠度、截面温度，并进行了动力测试。当受火时间达到15 min时，发现火灾试验炉内产生水蒸气，并伴有混凝土的爆裂声。

1.1.1 温度场数据 通过火灾炉内4根测温杆测量炉内实时温度，使用安捷伦数据采集仪对试验梁截面温度进行温度采集，采集时间间隔设定为1 min，B-T12L44梁部分截面测点的温度变化如图4所示，3种不同工况下试验梁炉温曲线如图5所示。分析可知，由于试验梁距火灾炉喷火口距离较远，导致试验初期试验梁截面升温较慢。在100 ℃左右，混凝土各测点的温度出现一段平台期，离受火面越远，温度平台越长。主要原因是混凝土内部的水在100 ℃时蒸发，带走大量热量，使混凝土温度上升缓慢。

图4 截面1各测点温度变化(1/3跨度)Fig. 4 Temperature change of section 1(1/3 span)

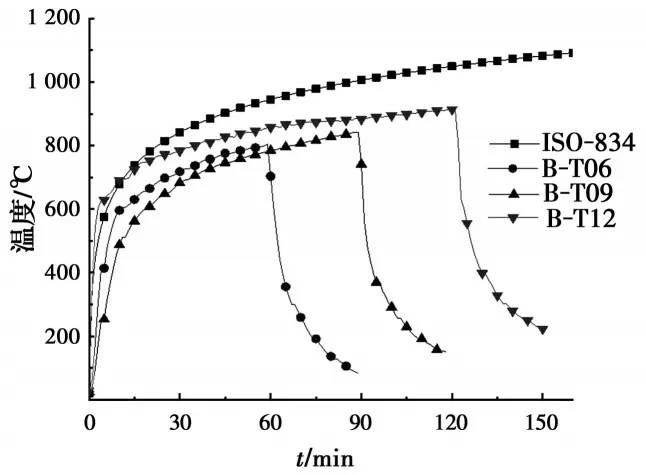
图5 炉温曲线Fig. 5 Furnace temperature curve

1.1.2 实测基频数据 采集火灾过程中振动信号，设定每隔1 min采集1次，火灾下采用环境激励进行测试，使用DH5922D动态信号测试分析系统对振型和频率进行分析，得到火灾后基频如图6所示。通过受火前、后实测的基频，可以得到不同工况下RC梁的振动特性衰减情况。更详细的数据参考文献[2,11]。

图6 火灾前、后实测基频Fig. 6 Measured fundamental frequency before and after fire

1.2 灾后静载试验

火灾试验后进行试验梁的静载试验，采用三点加载法，静力加载装置如图7所示。使用DH3816采集钢筋与混凝土应变数据，采用千斤顶来施加荷载，现场试验如图8所示。灾后梁刚度根据式（1）计算得到，限于篇幅，此部分数据详见文献[11]。

图7 静力加载装置示意图Fig. 7 Schematic diagram of static loading device

图8 静载试验装置及梁破坏图Fig. 8 Static load test device and bean failure diagram

式中：B为试验梁刚度；M为试验梁残余承载力；s为挠度系数，在集中荷载作用下s=1/12；f为简支梁跨中挠度；l0为简支梁计算跨度。

根据试验梁的残余承载力和挠度，按式（1）计算得到试验梁的刚度,结果见表2。

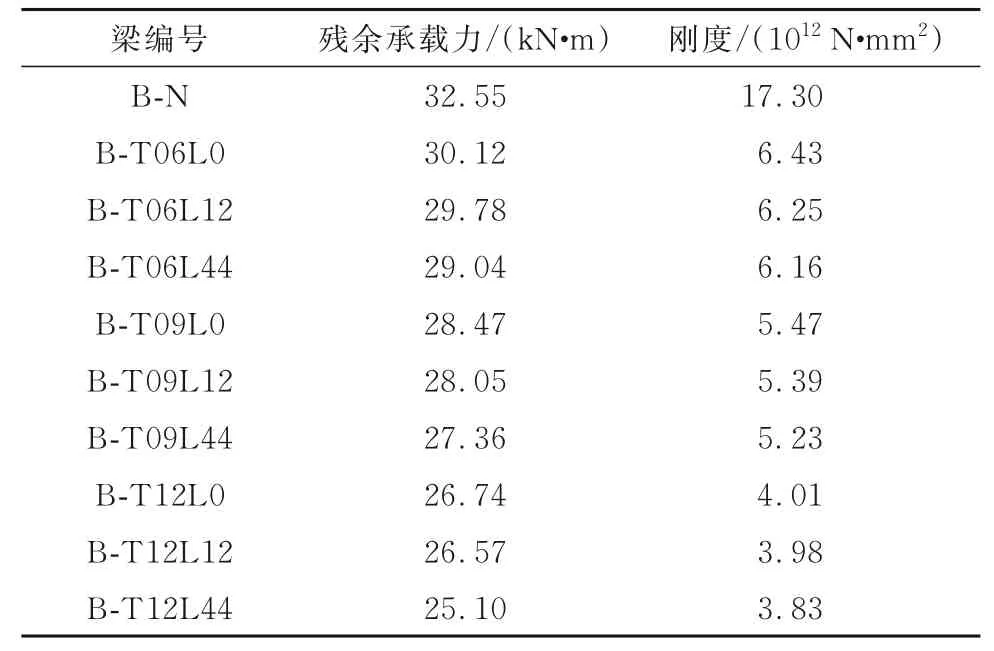
表2 残余承载力、刚度Table 2 Residual bearing capacity and stiffness

1.3 数值模拟分析

1.3.1 模型建立 材料的热工性能及高温下材料的力学性能参考文献[12]，高温后材料的力学性能参考文献[13]，利用ANSYS软件进行有限元分析，升温曲线采用试验炉温数据。SOLID70用于混凝土单元，LINK33用于钢筋单元，采用分离式建模方式。模拟工况考虑带裂缝、不带裂缝两种状态。受火前裂缝宽度为0.2 mm，深度为30 mm，受火90 min后裂缝宽度达到2.2 mm，裂缝深度达到71.6 mm，提前设定裂缝线性变化[14]。

1.3.2 截面温度场分析 通过建立的有限元数值模型[15]，模拟得到混凝土梁截面不同测点的温度变化，并与试验实测值对比分析，如图9所示，从中可以看出：实测温度值比模拟值大，其原因是实测过程中除5条主裂缝外，还有较多龟裂裂缝，在建模时无法考虑其影响，从而导致实测截面温度较高。

图9 B-T12L44各个截面测点温度变化Fig. 9 Temperature variation of each section of B-T12L44

1.3.3 灾后刚度和承载力分析 通过数值模拟可得到截面温度场分布、灾后刚度及承载力，进而得到火灾后梁的抗弯刚度和承载力的衰减曲线,见图10，静载后跨中挠度曲线见图11。由图10可知，抗弯刚度在大约30 min内迅速降低，30 min后下降缓慢，后期趋于平缓；在受火2 h后，构件的刚度损失约80%。高温后，抗弯承载力下降较小，受火2 h后，构件的抗弯承载力损失约20%，较刚度损失小。由图11可知，跨中挠度在加载初期随着荷载的增加呈线性变化，且增长幅度较小，当荷载施加达到极限荷载的90%左右时，挠度出现大幅度增长，继续施加荷载，受压区混凝土被压碎，此时荷载突然变小，构件失去承载能力。挠度试验值和模拟值变化相差较小，基本满足要求。此外，将部分梁的抗弯刚度、承载力的数值模拟结果与实测结果进行对比,结果如表3所示。由表3可知，理论值与试验值吻合度较高，进而证明了模拟的准确性。

表3 刚度、承载力值对比Table 3 Comparison of stiffness and bearing capacity

图10 抗弯刚度、承载力折减系数Fig. 10 Reduction factor of flexural stiffness and bearing capacity

图11 荷载—跨中挠度曲线Fig. 11 Load-mid-span deflection curve

2 RC梁灾后损伤多元信息综合评估方法

2.1 火灾损伤综合评估指标体系构建

单因素评估不能全面反映火灾后结构的整体性能，需要对构件进行多目标的综合评估。为更准确地评估灾后损伤，结合相关规范及参考文献，建立了火灾损伤综合评估的指标体系，评估指标包括表观现象、表面最高温度、承载力折减、基频折减、刚度折减、受火时间等6个指标。

2.2 损伤评估的MTOPSIS-GRA模型

TOPSIS是一种多目标决策分析方法[16]，采用正交投影法对其进行修正[17]，使TOPSIS所得解更接近正理想解和负理想解。GRA是一种多因素分析方法，可用来分析和评估方案与正、负理想解之间的关联程度。通过层次分析法(AHP)[9]和熵权法(EWM)分别得到指标权重的主、客观权重，采用离差平方和最优化法对客观权重和主观权重进行组合优化[18]。具体计算步骤为：1）最优指标和判断矩阵的确定；2）矩阵归一化处理；3）计算加权标准化矩阵；4）基于理想解计算灰色关联度。

将原始灰色评估体系的最优解替换为多目标

决策的正、负理想解，相应关联度系数为

式中：ξ为分辨系数，此处取0.5。

求平均值，得到αij与α+ij、α-ij的关联度为

计算融合改进逼近理想解法和灰色关联度法得到的距离和关联度，对结果进行标准化处理，计算公式为

式 中：Mi分 别 代 表Pi、R+i、Ri。Pi、Ri数值越大，越远离最优解，定义Pi*=1/Pi，则Pi*、R+i结果越大，越接近最优解。

构造综合关联度为

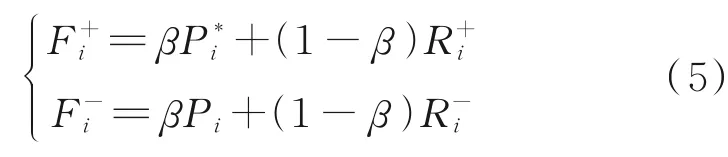
式中：F+i、Fi表示与理想方案接近和远离的程度，Fi+数值越大表示评估对象越优，Fi则相反；β为偏好系数，表示静态位置和趋势的偏好程度，在0～1范围内取值。数值量化可以用有维宝[19]的方法得到。

综合相对贴近度为

3 评估结果验证

3.1 灾后损伤初步鉴定

根据规范[1]得到火灾后混凝土梁的初步评级标准，邀请相关检测专家对9根试验梁火灾后的损伤进行评估和分级，得出损伤等级如表4所示。

表4 试验梁火灾后初步损伤评级Table 4 Preliminary damage rating of test beam after fire

3.2 确定指标评估标准

根据评估指标、标准及相关专家建议结果，确定各指标风险域。指标等级风险划分依据规范[1]和文献[2]分为Ⅱa、Ⅱb、Ⅲ、Ⅳ4级。等级量化后的具体指标见表5。

表5 损伤评估建议准则Table 5 Recommended guidelines for damage evaluation

根据理论计算值确定等级量化界限值，根据火灾发生的时间划分指标界限值，选取指标的3个边界作为一个工况，分别命名为边界1、边界2、边界3，并将其纳入到评估体系中，确定总体评估的贴近度和评估等级。

1）通过计算确定指标的主、客观权重。

2）运用综合赋权法确定综合权重值。

非负定矩阵

获得对称矩阵为WTA1W，计算结果为

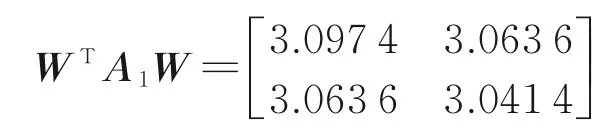
单位化特征向量为

得到优化组合权重为

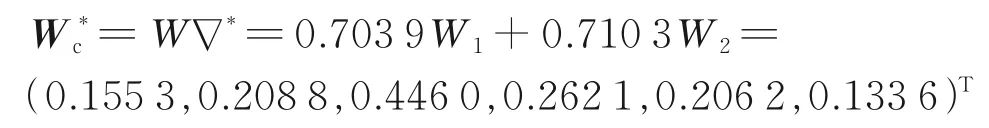
将加权向量归一化后，得到最优综合权重值W*c=

3）采用MTOPSIS-GRA进行数据优化，得到损伤等级划分贴近度值。

无量纲规范化矩阵为

为了避免计算的繁琐，对指标分别乘以系数100，得到加权矩阵

根据正负理想解的判别准则，对矩阵进行平移，得到结果

计 算 值 为：P1=0、P2=61.855 0、P3=119.154 6。

根据灰色关联度的计算方法，关联度系数矩阵为

加 权 关 联 度 为R+11=1、R+12=0.658 5、R+13=0.583 8、R-11=0.485 5、R-12=0.647 6、R-13=1。

运用MTOPSIS-GRA进行标准化，得到无量

纲 化 评 估 值P1=0、P2==0.519 1、P3=1、P1*=0、P2*==0.016 2、P3*=0.008 4、R+1=1、R+2=0.658 5、R+3=0.583 8、R-11=0.485 5、R-12=0.647 6、R-13=1

综合关联度为

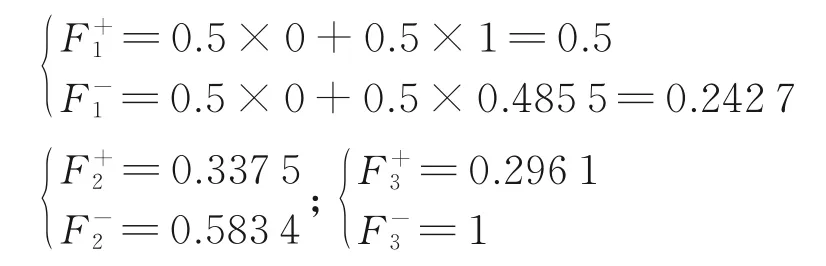
对于偏好系数β的取值，根据经验及参考文献[10]，且本文修正同时考虑两种方法，所以取β=0.5。

综合相对贴近度为F*1=0.673 2、F*2=0.366 5、F*3=0.228 4。

得到损伤等级对应的贴近度，见表6。

表6 试验梁损伤等级标准Table 6 damage grade of test beams

3.3 案例对比验证分析

将试验梁数据引入评估方法中，确定损伤等级，得到不带裂缝试验梁损伤评估贴近度为：BT06L0=0.665 5、B-T06L12=0.569 4、B-T09L0=0.407 1、B-T09L12=0.372 7、B-T12L0=0.232 4、B-T12L12=0.216 9。带裂缝梁的火灾后损伤评估 贴 近 度 为：B-T06L44=0.506 4、B-T09L44=0.349 4、B-T12L44=0.206 4，损 伤 评 估 结 果见表7。

由表7可以看出，8根火灾后试验梁评估得到的损伤等级与规范[1]得到的评级结果完全一致，说明该评估方法的适用性与合理性。BT09L12评级略有不同，原因在于此试验梁贴近度值位于等级边界处,导致评估结果略有不同。

表7 试验梁灾后损伤评估结果Table 7 Post-disaster damage assessment results of test beams

4 结论

对4组10个试件进行火灾—力学试验，研究火灾对T形梁刚度和承载力的影响，运用ANSYS对T形梁受火过程进行数值模拟，获取火灾中试验梁截面的温度场分布，并提出基于最优组合权重的MTOPSIS-GRA评估法，主要结论如下：

1）高温对钢筋混凝土梁破坏较严重，受火120 min后，T形梁刚度和承载力明显下降，刚度下降约80%，承载力下降约20%，同时延性增加，火灾前后T形梁的破坏形态相同。

2）提出了1种基于最优组合权重的多目标决策综合评估法，该评估方法考虑了规范[1]要求的因素，对主、客观权重采用离差平方和法得到组合权重，基于灰色关联度理论对改进逼近理想解进行优化，最终评级结果与规范中的评级结果一致，证明了其可行性，可为加固与修复方案制定提供支持。

3）在现有损伤评估规范的基础上，综合主、客观多种因素，将评估过程量化，把主观评定转变为数值计算，确定损伤等级，明确量化评估标准，提高了损伤评估的全面性和准确性，为后续损伤评估研究提供依据。