碳纤维增强速生杨胶合木梁的受弯性能

王玉镯,马云鹏,王兰芹,李沣庭

（山东建筑大学 土木工程学院，济南 250101）

因生长快和适应性强等特点，速生杨木在中国各地广泛种植，但由于其弹性模量和强度较低等特点，几乎没有应用到建筑结构中。中国木结构建筑所用木材长期依赖于进口，因此，若能增强速生杨木梁的力学性能，将其应用到建筑行业，将缓解中国木材供应紧张的局面，推动绿色建筑的发展[1-3]。

目前，学者们针对化学改性速生杨木的材料力学性能开展了一系列试验研究。岳孔等[4]进行了PF浸渍改性处理速生杨木的材料力学性能试验，结果表明，改性材料的顺纹抗压强度、抗弯强度和抗弯弹性模量较改性前分别提高了207.4%、22.1%和87.8%。岳孔等[5]进行了PF和UF浸渍改性处理速生杨木的材料力学性能试验研究，结果表明，PF浸渍改性材的抗弯弹性模量、抗弯强度、顺纹抗压强度和顺纹抗拉强度分别提高了97.1%、83.4%、125.5%和37.0%，UF浸渍改性材料相应指标分别提高了49.4%、10.7%、42.0%和17.8%。王娱等[6]研究表明，PF浸渍改性速生杨木优化的工艺条件为真空度0.08 MPa、真空度稳定时间15 min、恢复常压时间140 s、常压浸渍时间8 min。物理改性速生杨木的材料力学性能方面，刘庆娟等[7]对不同板材厚度和不同纹理的改性速生杨木进行了力学性能试验研究，表明改性材料的抗压强度和弹性模量随着板材厚度的减小而显著增大；最佳组合方式为顺纹加顺纹，最佳粘贴方式为弦向粘贴。

学者们还进行了钢板和各种纤维布[8-12]加固木构件的试验研究。许清风等[8]对粘贴钢板加固的8根木梁进行了对比试验研究，试验参数包括钢板厚度(3 mm或5 mm)、钢板层数(1或2)和是否采用螺栓锚固，结果表明，粘贴钢板加固木梁的极限承载力提高了9%～141%；其中，采用螺栓锚固粘贴钢板加固木梁的极限承载力提高幅度更大，平均提高了88%。潘毅等[9]对BFRP布底部粘贴、底部与侧面环向粘贴、底部与侧面螺旋缠绕粘贴的加固木梁进行了对比试验研究，结果表明，与未加固试件相比，其极限荷载分别提高了16.30%、24.34%和30.54%。Glišović等[10]进行了受拉侧粘贴碳纤维布加固胶合木梁的受弯试验，加固后试件的强度、刚度和延性均表现良好。

Thorhallsson等[11]进行了受拉侧粘贴不同厚度玄武岩纤维布加固胶合木梁的受弯试验，结果表明，加固后木梁的强度提高了37%～57%，弹性模量提高了11%～21%，最佳的玄武岩纤维布配比率为0.2%～5%。Vahedian等[12]对不同粘结长度、宽度和厚度的FRP加固木梁进行了试验研究，结果表明，试件的韧性随着纤维厚度的增加而增加，极限抗弯强度随着粘结宽度和长度的增加而增大。上述研究大多集中在将钢材或纤维材料粘贴在梁的外部或梁的受拉侧，配置位置的变化方式较少。

有学者对FRP板/筋、预应力筋等增强木构件的力学性能开展了研究。Yang等[13]进行了FRP板、钢材增强胶合梁试验，考虑了增强材料、配比率和配置方式等因素，结果表明，与纯胶合试件相比，木材的抗弯承载力、抗弯整体刚度和破坏时的拉应变平均增强率分别达到56.3%、27.5%和49.4%。许清风等[14-15]进行了内嵌CFRP筋/片加固木梁的受弯试验，结果表明，加固后损伤木梁受弯承载力可完全恢复并有一定提高；试件的受弯承载力提高了14%～85%，平均提高39%；破坏位移平均提高了32%。张晋等[16]进行了不同形式预应力筋增强胶合木梁的受弯试验研究，结果表明，相对于抛物线形预应力筋增强试件，直线形试件受弯极限承载力更佳；相对于无粘结预应力筋试件，有粘结试件短期受弯性能更好。

大量研究集中在化学改性木材的材料力学性能和木构件的加固等方面，化学改性虽然能通过浸渍等方式改善速生杨木材质本身的缺陷，但其力学性能的改变幅度很小；物理改性基于木材本身的纹理特质进行不同方式的组合，以改善速生杨木的力学性能，但工艺较复杂；从现有文献来看，物理改性后木材的力学性能提高幅度大于化学改性。笔者采用速生杨木层板、结构胶和碳纤维等材料重新组合压制，得到6根整体性较高的碳纤维增强速生杨胶合木梁，对其进行受弯试验，研究不同配纤率和不同配纤位置等因素对梁破坏形态、承载能力及变形能力的影响。

1 试验概况

1.1 试件设计

依据ISO 8375-2017[17]和《木结构试验方法标准》（GB/T 50329—2012）[18]等规范，考虑不同配纤率和不同配纤位置等因素的影响，共设计了6根试件，包括1根纯胶合木对比试件（W1）和5根增强速生杨胶合木试件（P1、P2、P1-1、P2-1、P2-2）。如图1所示，试件P1下部配置1层碳纤维，试件P1-1上部与下部各配置1层碳纤维，试件P2下部配置2层碳纤维，试件P2-1下部配置2层碳纤维且上部配置1层碳纤维，试件P2-2上部与下部各配置2层碳纤维。试件截面尺寸为50 mm×120 mm，长度为2 300 mm。其中，试件采用的木板厚度为12 mm，碳纤维布厚度为0.167 mm，宽度和长度均与木板尺寸相同，并保证碳纤维平整且纤维方向与试件的长度方向一致。

图1 试件截面示意图Fig. 1 Schematic diagram of specimen section

试件各材料之间采用结构胶粘接，粘接之前对速生杨木板材表面进行清理、打磨、整平和缺陷位置记录。首先将结构胶在一块木板表面涂抹均匀，将碳纤维布（按照纤维方向与构件长度方向一致放置）平整地铺在胶层表面；然后将另一块涂满结构胶的木板置于上方，并压紧、压实；最后再采用同样的方法施工其他粘结层，直至施工完成。在完成后的试件上放置一定质量的钢块，48 h后取下，以确保各板层之间粘接紧密。试件的具体参数如表1所示，试件的截面构造如图2所示。

表1 试件参数Table 1 Specimen parameters

图2 试件构造示意图Fig. 2 Schematic diagram of specimen

1.2 材料

试验所用木材取自山东济南5年生108速生杨，取树木中间段，在室内自然风干至含水率13.5%，符合规范要求的9%～15%。按照规范《木结构试验方法标准》（GB/T 50329—2012）[18]、《木材顺纹抗压强度试验方法》（GB/T 1935—2009）[19]、《木材顺纹抗拉强度试验方法》（GB/T 1938—2009）[20]中的材性试验可以测得木材的主要力学性能，见表2。试验所用的增强材料为碳纤维布和结构胶，结构胶的主要成分为环氧树脂和硬化剂（使用比例为1:1）。主要材性具体参数均由生产检测报告提供，见表3。

表2 木材主要性能参数Table 2 Main performance parameters of wood

表3 增强材料主要性能参数Table 3 Main performance parameters of reinforcement materials

1.3 加载装置与测点布置

试件与两端的支座之间均为铰接，支点位置设计在试件两端各内收70 mm处，即试件跨度为2 160 mm。为了防止试件发生侧向失稳，在支座处设置侧向支撑。在试件上方跨度1/3处各设置一个50 mm×50 mm×10 mm的钢垫，钢垫上方设置H型钢分配梁，分配梁上方设置液压千斤顶并连接中国航天BK-4C压力传感器进行荷载数据采集。试件布置和加载装置示意如图3所示。

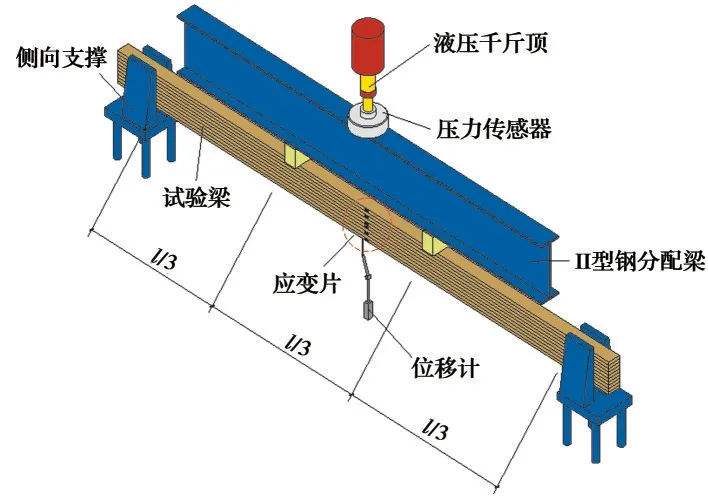
图3 加载装置与测点布置示意图Fig. 3 Schematic diagram of the arrangement of loading device and measuring point

为测量试验过程中梁中点挠度的变化，在梁跨中下方布置了位移计。为测量试验过程中木材的应变发展情况，在梁跨中的侧面布置了6个应变片（S1～S6）。位移计和应变片的数据采集使用TST2385F-L静态应变分析仪。各测点的编号和位置见图4。

图4 应变片布置示意图Fig. 4 Schematic diagram of strain gauge layout

1.4 加载制度

试验通过液压千斤顶进行三分点静力加载，首先采用循环加载制度，利用各试件的弹性，得到5次挠度无明显差异的荷载—位移曲线，从而对试件的弹性模量进行测量；循环范围为2～4 kN（速率2 kN/min）。之后，采用力控制的分级加载制度，每级荷载大小1 kN（速率1 kN/min），每级（循环）加载结束后稳定60 s并进行数据采集，直至梁破坏。加载制度曲线如图5所示。

图5 加载曲线Fig. 5 Loading curve

2 试验结果及分析

2.1 试件的破坏现象

在加载初期，木板没有出现裂缝；试件荷载达到极限荷载的73%～82%后，受拉区木板出现垂直和斜向细微裂缝，试件的挠度变形发展速度加快，同时出现“噼啪”断裂声。最终达到极限荷载，伴随“啪”一声巨响，试件发生脆性破坏，破坏发生于梁受拉区边缘木板，梁受拉区的破坏均属于木板断裂，未发现胶层破坏，如图6所示。

图6 试件破坏状态Fig. 6 Destruction state of specimen

1）对比受拉区配纤率的影响。试件W1受拉区边缘5层木板断裂，断裂后裂缝沿纵向发展，并导致木板沿梁长度方向撕裂分层且塌落。试件P1受拉区边缘3层木板断裂，同样出现了木板沿梁长度方向的撕裂分层，所配置的1层碳纤维随木板一起断开。试件P2受拉区边缘2层木板断裂，跨中偏左处受压区木板边缘隆起，所配置的2层碳纤维中下层的断开，上层的未断开。与试件W1相比，试件P1、P2裂缝少且细，受拉区木板断裂层数少。3个试件中，试件P2的裂缝宽度最小，受拉区木板断裂数量最少，且破坏时裂缝没有沿纵向发展，没有发生木板撕裂分层的现象。

2）对比配纤位置（单层）的影响。试件P1-1受拉区边缘3层木板断裂，受拉区碳纤维随木板一起断裂，受压区木材存在一个3 mm×2 mm的木节并出现斜向裂缝，受压区碳纤维未见异常。相对于试件W1、P1，试件P1-1受拉区裂缝分布少，挠度变形减小，且没有出现木板沿梁长度方向大范围撕裂分层的现象。

3）对比配纤位置（双层）的影响。试件P2-1受拉区边缘3层木板断裂，受压区边缘木板出现隆起和纵向裂缝，受拉区所配的2层碳纤维中，下层的断开、上层的未断裂，受压区碳纤维未见异常。试件P2-2受拉区边缘3层木板断裂，受压区边缘木材出现木纤维翘起和细微纵向裂缝，受拉区配置的2层碳纤维均断裂。试件P2、P2-1、P2-2受拉区裂缝分布和发展情况类似，试件P2-1变形较大，试件P2-2变形最小。试件P2和P2-1受压区木材隆起，试件P2-2受压区木纤维翘起。

2.2 试件的抗弯弹性模量

如图7所示，通过循环加载得到试件5次挠度无明显差异的荷载—位移曲线。取其中3次相近挠度差的平均值作为梁的挠度差测定值Δω，取相应的荷载增量ΔF，对每个试件的抗弯弹性模量E进行计算，如式（1）所示[17-18]，计算结果见表4。

图7 试件循环加载曲线Fig. 7 Cyclic loading curves of specimen

表4 试件抗弯弹性模量Table 4 Flexural elastic modulus

式中：a为加载点至支承点的距离；l为试件跨度；I为试件截面惯性矩。

2.3 试件的承载性能

试件的跨中荷载—挠度曲线如图8所示。所有试件的曲线形状类似：在加载初期，试件曲线基本呈线性变化，并且变化基本相同。随着荷载的增加，试件曲线呈非线性增长，挠度的增长速率大于荷载。当加载到极限荷载的73%～82%后，增强试件荷载曲线开始出现锯齿状下降，但还能继续增加荷载。达到极限荷载后，荷载曲线突然大幅下降，试件发生脆性破坏。

图8 跨中荷载—挠度关系曲线Fig. 8 Load-deflection curve of mid-span

为进一步对比碳纤维增强速生杨胶合木梁的受弯性能，将试件承载性能试验的主要结果列于表5中，其中，极限承载力P和对应的跨中挠度f均由试验直接测得；初始抗弯刚度EI通过式（1）计算得到。ρP为增强试件与纯胶合木试件极限荷载P的比值；ρEI为增强试件与纯胶合木试件初始抗弯刚度EI的比值。

1）对比受拉区配纤率的影响。试件的极限荷载随着试件受拉区配纤率的增加而增加，相对于W1试件，试件P1和P2的极限荷载分别提高了21.42%和50.72%；试件的初始抗弯刚度亦有所提高，相对于试件W1，试件P1和P2的初始抗弯刚度分别提高了12.37%和12.17%。表明速生杨木受拉区配纤的增强效果突出，受拉区加入碳纤维提高了试件的极限荷载和初始抗弯刚度。

2）对比配纤位置（单层）的影响。试件P1和P1-1的极限荷载分别为19.39、18.60 kN，两者相差不足5%，不能判定是试验误差还是受压区碳纤维所致；相对于试件P1，试件P1-1的初始抗弯刚度提高了9.79%，极限挠度减小了55%。表明受压区加入碳纤维对试件的极限荷载具有减小作用，但效果不明显；受压区加入碳纤维可以减小试件的极限挠度；对初始刚度有提高但效果不明显。

3）对比配纤位置（双层）的影响。相对试件P2，试件P2-1和试件P2-2的极限荷载分别降低了16.7%和4.5%；初始抗弯刚度提高了10.0%和5.7%；极限挠度降低了4.8%和1.9%。表明受压区碳纤维的增加对试件的极限荷载具有减小作用，但减小幅度不大；受压区加入碳纤维可以减小试件的极限挠度；对初始刚度有提高但效果不明显。

由此看出，在速生杨胶合木梁受拉区配置碳纤维时，能有效提高试件的极限承载力和初始抗弯刚度；相比仅在受拉区配置碳纤维，在受拉区和受压区均配置碳纤维布时，试件的承载力反而减小，但破坏时的挠度降低，初始抗弯刚度有提高但效果不明显。

2.4 试件的应变

2.4.1 荷载—应变曲线 试验可测得木材的荷载—应变关系，取所测边缘应变片S1和S6的数据进行对比，如图9所示，S1的压应变为负，S6的拉应变为正。当荷载达到极限荷载的73%～82%后，试件的边缘应变随着荷载的增加呈非线性变化。

图 9 荷载—应变关系曲线Fig.9 Load-strain relationship curves

1）对比受拉区配纤率的影响。试件的边缘极限应变随着受拉区配纤率的增加而增加，相比试件W1，试件P1和P2的边缘极限拉应变分别增加了5.81%和12.56%，边缘极限压应变分别增加了13.10%和22.76%。表明速生杨木受拉区配纤后木材的抗拉强度和抗压强度得到充分利用。

2）对比配纤位置（单层）的影响。由于受压区木材斜向裂缝的发展造成试件破坏，试件P1-1木材的应变没有得到充分发展。与试件P1相比，由于受压区木材斜向裂缝的发展造成试件破坏，试件P1-1边缘极限拉应变降低了18.58%，边缘极限压应变降低了20.71%。

3）对比配纤位置（双层）的影响。与P2相比，P2-2的边缘极限拉应变提高了8.66%，边缘极限压应变提高了3.93%；P2-1的边缘极限拉应变提高了1.76%，边缘极限压应变没有明显变化。

由此看出，木材的拉应变和压应变主要受试件受拉区碳纤维布层数的影响，且随着试件受拉区配纤率的增加而增加；试件受压区配置碳纤维布对木材的边缘极限拉应变和压应变影响较小。另外，在试件受压区布置碳纤维时，加载后期试件的胶层与碳纤维受压堆积出现裂缝，导致试件破坏，从而使木材的塑性受压性能得不到充分发展。

2.4.2 截面高度—应变曲线 由所测应变片S1～S6

的数据得到试件在各级荷载下跨中应变—截面高度曲线，如图10所示。曲线基本呈线性分布，接近破坏荷载时，由于开裂或破坏，个别试件曲线出现轻微偏离，但对于分析试件加载过程或开裂时的应变没有影响，因此，试件在加载中的应变分布符合平截面假定特征。

图10 试件的截面高度—应变曲线Fig. 10 Section height-strain curves of specimen

3 理论模型

碳纤维增强速生杨胶合木梁破坏时受拉区木材均发生强度破坏，而根据所测应变，受压区木材破坏状态分为两种，即弹性和塑性。在极限荷载下，破坏状态不同的梁，其木材和碳纤维的应力—应变状态也不同。因此，结合截面平衡理论，建立两种不同破坏模式下梁受弯破坏时的极限弯矩理论计算模型，并提出相应的计算方法。

3.1 基本假定

做以下假定：

1）试件截面的应变分布符合平截面假定；

2）碳纤维与木材之间粘结可靠；

3）试件受弯时，受压、受拉、受弯弹性模量相等；

4）忽略碳纤维厚度对试件整体高度的影响；

5）木材受拉时为线弹性；受压时采用Bazan[21]和Buchanan[22]的双线性模型，见图11（a）。

6）碳纤维受拉时为线弹性材料，沿厚度方向应力均匀；受压时应力为0，见图11（b）。

图11 材料的应力—应变关系曲线Fig. 11 Stress-strain relationship curves of materials

3.2 材料的应力—应变关系

由图11（a）得到木材的应力—应变关系为

式 中：εt和σt为 木 材 的 拉 应 变 和 拉 应 力；εc和σc为 木材的压应变和压应力；εcy为木材的弹—塑性界限压应变；εcu为木材的极限压应变；E为木材的弹性模量；Em为木材的塑性受压系数,如式（3）所示。

由图11（b）得到碳纤维应力—应变关系为

式中：εp和σp为碳纤维的拉应变和拉应力；Ep为碳纤维的弹性模量。

3.3 不同破坏状态下试件的界限划分

图12为试件跨中截面应变分布和应力分布简图，其中,H为试件截面高度；nh为碳纤维下部n个木板厚度；X为截面受压区高度；α为塑性受压区高度系数（塑性受压区高度与总受压区高度之比）；Ft为木材拉应力合力；Fc为木材未进入塑性时压应力的合力；Fc1为木材进入塑性时弹性阶段压应力的合力；Fc2为木材进入塑性时塑性阶段压应力的合力；Fp为碳纤维拉应力的合力,如式（5）所示。

式中：A1为单层碳纤维的横截面面积。

首先，由平截面假定得到H、X、nh和α的比例关系式，见式（6）。

进一步，根据试件破坏时受压区木材的应力—应变情况，将试件的破坏状态分为两种：当εc≤εcy时和当εu≥εc＞εcy时。图12（b）、（c）、（d）即试件跨中截面应变分布示意图及两种破坏状态下的截面应力分布示意图。

当εc≤εcy时，根据图12（c）和式（2）可得到此状态下木材应力的合力，如式（7）所示。

由水平方向荷载的平衡条件∑F=0得到合力平衡关系式，见式（8）。

将式（7）代入式（8），可得式（9）。

此类破坏情况在试件受拉区配纤率过小时发生，受拉区木材断裂后，碳纤维立即发生强度破坏，但受压区木材仍处于弹性阶段，试件的极限承载力主要与木材的抗拉强度有关。

进一步，为进行试件不同破坏状态的界限划分，令试件的受拉区配纤率ρ=nA1/bH，将式（6）代入式（9）中，可得到此类破坏发生时受拉区配纤率表达式，见式（10）。

当εu≥εc＞εcy时，根据图12（d）和式（2），可得到此状态下木材应力的合力表达式，见式（11）。

图12 试件跨中横截面应力和应变分布Fig. 12 Stress and strain distribution of the cross section of specimen

由水平方向荷载的平衡条件∑F=0得到合力平衡关系式，见式（12）。

将式（11）代入式（12），可得到式（13）。

此类破坏情况在试件受拉区配纤率适中时发生，受拉区木材断裂后，碳纤维发生强度破坏，受压区木材已经进入塑性，试件的极限承载力主要与受拉区碳纤维配纤率有关。将式（6）代入式（13）可得到此类破坏发生时的受拉区配纤率。

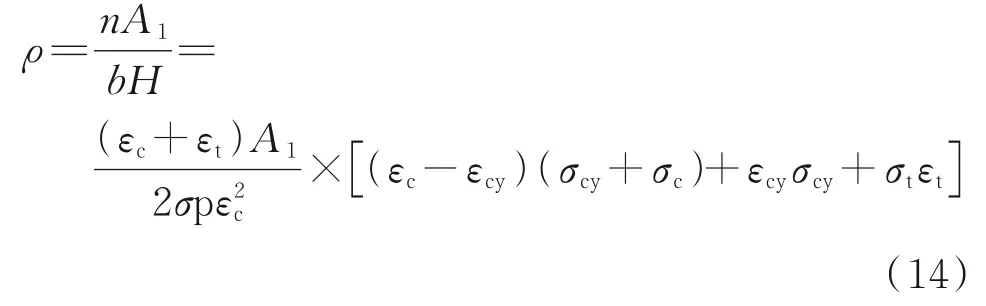
根据试件的不同破坏特征，取εt=εtu，εc=εcy，σt=0，σc=fcu，σp=fpu,代 入 式（10）可 得“εc≤εy”和“εu≥εc＞εy”，破坏的界限受拉区配纤率ρmin=0.060 6%。取εt=εtu，εc=εcu，σc=σcy-(εcu-εcy)，σt=0，σp=fpu，代入式（14）可得“εu≥εc＞εcy”，破坏的受拉区最大配纤率ρmax=1.031 1%。

因此，当0.060 6%＜ρ＜1.031 1%时，试件破坏时碳纤维和受压区木材的性能可以得到充分利用。

3.4 不同破坏状态下试件的极限弯矩计算

根据不同破坏模式，通过平截面假定和截面平衡理论，由截面中和轴∑M=0可以得出试件的极限弯矩Mu。其中，由于木材本身不可避免地存在生物质材料缺陷，经过统计试件的缺陷数量和缺陷位置，添加一个不确定系数“γ=0.9”，考虑各种不确定因素对木梁承载力的影响并对Mu进行折减。

当εc≤εy时，将式（7）代入∑M=0可得到极限弯矩计算式式（15）。

当εu≥εc＞εcy时，将式（11）代入∑M=0可得到极限弯矩计算式式（16）。

3.5 计算结果的对比

增强试件受拉区配纤率为0.139%和0.278%时,根据破坏现象和应变分析，破坏时试件受压区木材表现出了部分塑性，可以通过式（16）进行极限弯矩计算。而未增强试件破坏时受压区木材则未进入塑性，可以通过式（15）进行极限弯矩计算。计算过程如表6所示，其中，X.Cal通过式（6）得出。试件的极限弯矩理论值Mu.Cal如表7所示，并与试验值Mu.Exp进行了对比。与试验值相比，试件极限弯矩的理论计算值普遍偏大，整体吻合较好，计算公式能准确预测此类试件的极限弯矩。误差主要是由木材内部的不稳定性、木质的缺陷等原因导致的，在进行工程应用时，应该充分考虑木材的缺陷。

表6 Mu.Cal计算Table 6 Calculation of Mu.Cal

表7 计算结果Table 7 Calculation results

4 结论

通过分析不同配纤率、配纤位置等因素对增强速生杨胶合木梁破坏状态、承载能力和变形能力的影响，得出以下主要结论：

1）碳纤维增强后梁的裂缝数量减少、裂缝宽度减小且受拉区断裂木板数量减少，试件的变形减小。

2）碳纤维增强后梁的受力性能优良，组合效应突出，相比速生杨木,增强后试件的弹性模量提高幅度为28.02%～57.93%；相比纯胶合木试件，极限荷载提高了16.47%～50.72%，初始抗弯刚度提高了11.58%～23.37%。其中，随着梁受拉区配纤率（1层、2层）的增加，试件的极限荷载分别提高了21.42%和50.72%，试件的初始抗弯刚度分别提高了12.37%和12.17%。

3）相比仅在受拉区配置碳纤维，在受拉区和受压区均配置碳纤维布时，试件的承载力反而减小，但破坏时的挠度降低，初始抗弯刚度有提高但效果不明显。

4）与纯胶合木试件相比，增强试件边缘木材的极限压应变提高了15.11%～51.97%，增强后充分利用了木材的抗压强度，且试件在破坏时表现出部分塑性性能。

5）当试件受拉区配纤率处于0.060 6%～1.031 1%之间时，试件破坏时能充分利用木材的塑性抗压性能和碳纤维的抗拉性能。根据试件不同的破坏模式，利用试件极限弯矩简化计算的结果与试验结果吻合较好，计算结果能较好地预测此类试件受弯时的极限弯矩。