多模型广义标签多伯努利滤波器

辛怀声, 宋鹏汉, 曹 晨

(中国电子科技集团公司电子科学研究院, 北京 100041)

0 引 言

随时间传递多目标后验密度的贝叶斯多目标滤波器是解决多目标跟踪问题的贝叶斯最优解[1]。在标准多目标系统建模下,由于多目标后验密度服从广义标签多伯努利(generalized gabeled multi-Bernoulli, GLMB)分布[2],因此基于GLMB分布得到的贝叶斯滤波器就成了最优的多目标滤波器,也就是GLMB滤波器或Vo-Vo滤波器[3-4]。但值得注意的是,GLMB滤波器并没有对目标的运动模型进行深入分析。

研究表明,运动模型与真实运动之间的失配是机动目标跟踪面临的一个最主要的挑战[5],在随机有限集多目标跟踪算法中这也是影响跟踪机动目标的最关键因素之一。运动模型的失配往往导致时间预测步骤得到的状态转移密度与目标的真实运动状态完全背离,进而引起后续关联和跟踪的彻底失败。针对这个问题的一个有效解决手段是引入马尔可夫跳变系统(jump Markov system,JMS)。引入JMS后目标的运动模型可以在一个运动模型集之内切换。一些基于JMS的多模型随机有限集滤波器被陆续提出,例如多模型概率假设密度(multiple model probability hypothe-sis density, MM-PHD)[6-9],多模型势集概率假设密度(multiple model cardinalized probability hypothesis density, MM-CPHD)[10],多模型多伯努利(multiple model multi-Bernoulli, MM-MB)[11-12],多模型标签多伯努利(multiple model labeled multi-Bernoulli, MM-LMB)[13-15]。近期为了扩展GLMB在机动目标跟踪领域的适用性,多模型GLMB(multiple model GLMB, MM-GLMB)算法[16-18]被提出来,这类MM-GLMB算法首先对带标签的目标运动状态进行扩展,然后基于JMS和目标的扩展运动状态对GLMB的预测和更新方程进行推导,从而得到多模型算法的闭式解,所以MM-GLMB算法也被称为JMS-GLMB算法。然而,完整的JMS-GLMB算法存在JMS分支规模成指数增长的问题,无法实现,因此已有的JMS-GLMB算法都采取了剪枝近似的方式控制跳变分支的规模。

与剪枝策略对应的,目前流行的多种经典多模型算法,例如交互多模型(interacting multiple model, IMM)、变结构多模型(variable-structure multiple model, VS-MM)[19-23]和广义伪贝叶斯(generalized pseudo Bayes, GPB)[24],均采用基于条件概率的分支合并策略解决JMS分支的规模膨胀问题,在跟踪精度和计算复杂度方面均优于采取剪枝策略的多模型算法,而已有的MM-GLMB算法还没有采用分支合并策略的解决方案。

本文将马尔可夫分支合并策略与GLMB算法结合,提出了3种多模型GLMB算法,分别为IMM-GLMB、一阶GPB-GLMB (GPB1-GLMB),以及二阶GPB-GLMB (GPB2-GLMB),并通过蒙特卡罗仿真对所提算法与JMS-GLMB进行比较,验证了所提算法在精度和计算时间两个方面都优于JMS-GLMB,尤其在计算时间上优势明显。

下面章节中,第1节首先简要介绍JMS和JMS-GLMB滤波算法的背景知识,在第2节至第4节中参照IMM和GPBn的分支合并策略给出IMM-GLMB、GPB1-GLMB和GPB2-GLMB这3种滤波器的递推公式和高斯混合实现。第5节通过仿真对所提出的3种算法与JMS-GLMB进行对比。第6节对所提的3种滤波器做出结论。

1 背 景

1.1 JMS简介

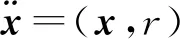
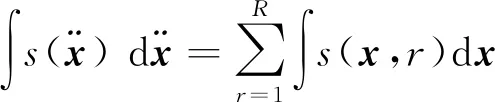
(1)

定义马尔可夫模式跳变概率矩阵为

(2)

式中:χi, j表示模式rj跳变到模式ri的概率。

接下来对目标状态转移密度使用贝叶斯规则,可以得到马尔可夫状态转移密度如下所示:

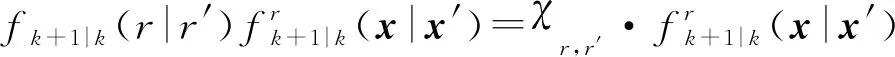
(3)

1.2 JMS-GLMB滤波算法

假设目标的运动模式跳变历史可以用索引ς进行标记。pς为跳变历史ς的概率。因此,按照贝叶斯全概率公式单目标的分布密度可以写为

(4)

假设经过k次迭代后多目标后验分布满足标签多伯努利分布,如下所示:

(5)

式中:X为多目标状态的随机有限集;o′表示多假设的索引。将带标签和模式变量的目标增广状态分布s(x,l,r)以及式(1)～式(4)代入GLMB的时间预测方程中，可以得到JMS-GLMB的时间预测步骤结果,如下所示:

(6)

式中:

(7)

(8)

(9)

(10)

(11)

(12)

假设k+1时刻量测集合为Zk+1,则JMS-GLMB的观测更新步骤如下所示:

(13)

式中:

(14)

(15)

(16)

(17)

(18)

(19)

新的运动模型跳变分支概率如下所示：

(20)

式中:归一化参数

ςk+1表示k+1时刻的模式跳变分支索引,由k+1时刻的模式r与k时刻的跳变历史索引ςk组合而成,如下所示:

ςk+1=(r,ςk)

(21)

θ函数为航迹标签到量测的关联映射;κ(z)函数为杂波强度函数,κ(z)=λ·c(z),c(z)为杂波空间密度,杂波数量服从泊松分布;λ为泊松分布的均值。

通过式(10)可知,在JMS-GLMB滤波迭代过程中,单目标的模式跳变分支数量会随每次预测迭代增长R倍,即按照运动模型集合的势成指数增长。为了易于实现,在观测更新结束后需要进行剪枝,以保持分支总体规模的稳定。

2 IMM-GLMB滤波器

参考IMM在预测前进行目标运动状态混合的思路,IMM-GLMB可以通过模式条件概率将多目标状态分布进行多模式合并近似,解决马尔可夫模式跳变分支的数量爆炸问题。

2.1 IMM-GLMB滤波算法

假设经过k轮迭代后多目标GLMB先验密度如下所示:

(22)

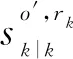
(23)

单目标分布混合密度:

(24)

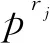
(25)

根据IMM算法有:

完成状态混合后,进行时间预测步骤,多目标时间预测分布密度函数为

(26)

式中:

(27)

ps(x′,l,r)·fr,l(x|x′)dx′

(28)

(29)

(30)

(31)

(32)

假设k+1时刻观测集合为Zk+1,则观测更新步骤后多目标密度可以表示为

(33)

式中:

(34)

(35)

(36)

(37)

(38)

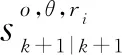
模式概率更新方程如下所示:

(39)

2.2 IMM-GLMB的高斯混合实现

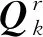
(40)

目标的状态混合密度为

(41)

式中:

(42)

(43)

将式(41)代入式(25)可以得到多目标时间预测表达式：

(44)

(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

(53)

(54)

(55)

(56)

目标状态提取方程为

(57)

对应协方差为

(58)

模式概率更新方程为

(59)

3 GPB1-GLMB滤波器

区别于IMM-GLMB,GPB1没有预测前混合步骤,或者可以认为GPB1为χi, j全相等条件下的特殊混合形式的IMM。

3.1 GPB1-GLMB滤波算法

设经过k次迭代后多目标先验分布密度如式(5)所示,则时间预测步骤后的多目标密度为

(60)

(61)

(62)

(63)

ps(x′,l,r)·fr,l(x|x′)dx′

(64)

(65)

(66)

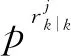
GPB1-GLMB的观测更新步骤如下所示:

(67)

式中:

(68)

(69)

(70)

(71)

(72)

(73)

目标状态提取如下所示:

(74)

模式概率更新方程如下所示:

(75)

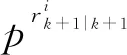
3.2 GPB1-GLMB的高斯混合实现

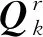
(76)

(77)

(78)

(79)

(80)

(81)

设线性高斯条件下量测矩阵为Hk+1,则观测更新步骤的高斯混合实现为

(82)

(83)

式中:

(84)

(85)

(86)

单目标分布密度为

(87)

合成单目标分布密度:

(88)

则状态提取表达式为

(89)

(90)

模式概率的更新为

(91)

4 GPB2-GLMB滤波器

4.1 GPB2-GLMB滤波算法

参考GPB2的滤波架构,单目标分布密度在每次迭代中需要进行R2个模式分支计算,并根据量测似然度更新模式概率,合并模式分支。

假设k时刻多目标先验GLMB分布密度为

(92)

则时间预测分布密度可以表示为

fk+1|k(X)=

(93)

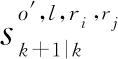
(94)

(95)

(96)

(97)

(98)

通过式(93)可以看出经过预测步骤后表示每个目标的R个模式分支增加到了R2个。

GPB2-GLMB的观测更新步骤如下,更新后多目标的GLMB密度为

(99)

其随机集权重和单目标分布密度为

(100)

(101)

式中:

(102)

(103)

(104)

(105)

(106)

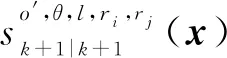
完成观测更新后,还需要进行状态合并:

(107)

(108)

(109)

模式更新为

(110)

归一化参数:

从式(107)、式(109)可以看出,经过观测更新后R2个分支密度被合并为R个,使得表示单个目标的分支数量保持稳定,避免了马尔可夫模式跳变分支数量呈指数增长的问题。

4.2 GPB2-GLMB的高斯混合实现

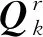
(111)

(112)

(113)

(114)

(115)

(116)

(117)

(118)

(119)

(120)

(121)

(122)

(123)

(124)

k+1时刻的目标合并分布为

(125)

(126)

(127)

模式概率更新为

(128)

式中:归一化参数

5 仿 真

5.1 环境设置

下面设置一个两维跟踪场景,比较JMS-GLMB与本文提出的IMM-GLMB、GPB1-GLMB和GPB2-GLMB这3种滤波器的机动多目标跟踪性能。仿真场景设置如下,传感器位于坐标原点(0,0) m,传感器量测周期T=8 s。多个机动目标在[0,150 000] m×[-20 000,100 000] m观测区域内运动。运动模型集由一个匀速运动(constant velocity, CV)模型、一个右转模型(5°/s转弯速率的协同转弯(corrdinated turn, CT)模型和一个左转弯模型(-5°/s转弯速率的CT模型)组成。3个运动模型的状态转移矩阵如下所示。

CV的状态转移方程为

右转模型(CT,ω1=5π/180)的状态转移方程为

左转模型(CT,ω2=-5π/180)的状态转移方程为

过程噪声协方差矩阵：

过程噪声方差对于CV模型取σv1=5 m/s2,对于CT模型取σv2=σv3=20 m/s2。

马尔可夫状态转移概率矩阵给定如下：

5个机动目标的存活概率设为ps=0.99,初始状态设置如表1所示,各个目标运动模型转换的时序如图1所示。

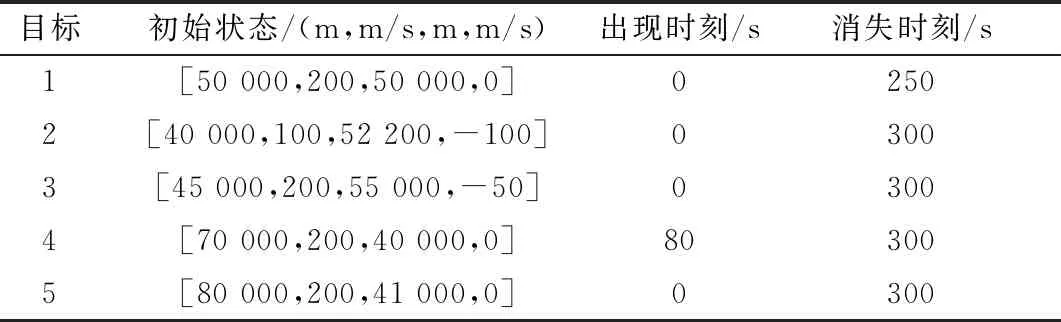
表1 目标初始状态表

图1 目标运动模型转换时序图

目标的真实运动路径如图2所示。

图2 目标运动轨迹

由于标准GLMB采取的已知新生目标分布策略会导致断批目标航迹无法重新起始,所以本文的算法均采用逻辑法进行航迹起始,确保目标航迹中断后可以重新起始。

量测方程采用极坐标形式,d为目标距离,α为目标方位角。xsensor为传感器的X轴坐标,ysensor为传感器的Y轴坐标。

量测方差设置如下:

方位角标准差σα=0.1π/180,测距标准差σd=50 m。每个扫描周期的杂波点数服从均值为λ的泊松分布,每个杂波点的位置在观测范围内均匀分布。最优子模型分配(optimal sub-pattern assignment,OSPA)[25]的参数设定为c=200 m,p=3。为了定量对OSPA曲线进行排名,对OSPA按时间统计其均值TOSPA,定义如下:

式中:OSPAk为时刻k对应的OSPA误差;S为单次仿真运行的计算迭代次数。

5.2 仿真结果分析

在给定目标探测概率pd=0.95,杂波率λ=5的情况下,对每个滤波器进行150次蒙特卡罗实验,计算时间消耗的对比如表2和图3所示。

表2 4种MM-GLMB滤波器的平均计算时间对比(λ=5)

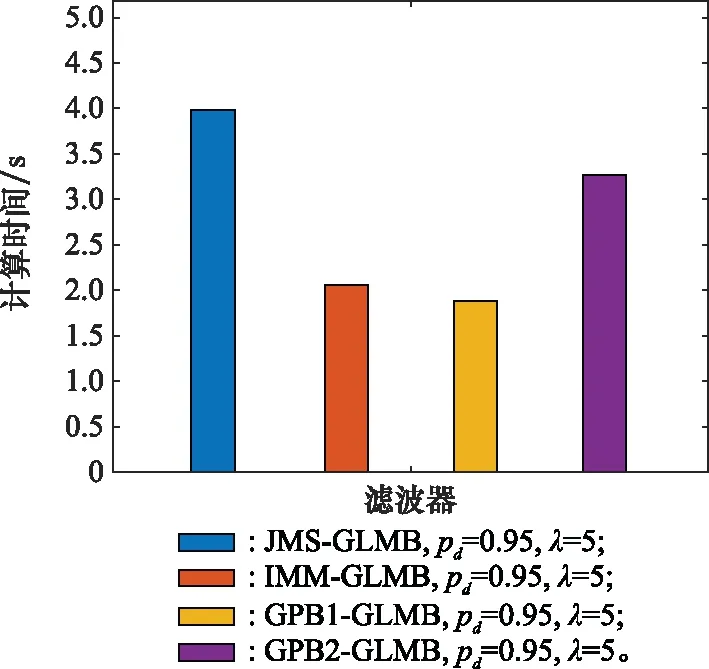
图3 4种MM-GLMB滤波器的计算时间消耗对比(λ=5)

OSPA误差对比如图4所示。

图4 4种MM-GLMB滤波器的OSPA航迹跟踪误差对比

可以看出,GPB1-GLMB、IMM-GLMB以及GPB2-GLMB跟踪精度都要优于JMS-GLMB。其中,GPB2-GLMB精度最高,IMM跟踪精度次之,GPB1-GLMB的精度排在第三名。另外,通过计算时间消耗对比可知,GPB1-GLMB消耗时间是最小的,JMS-GLMB消耗时间最多。

下面讨论4种滤波器在高杂波率和低探测概率情况下的表现。首先在杂波率λ=30,探测概率pd=0.95的情况下,进行150次蒙特卡罗实验。

计算时间消耗对比如表3和图5所示。

表3 4种MM-GLMB滤波器的平均计算时间对比(λ=30)

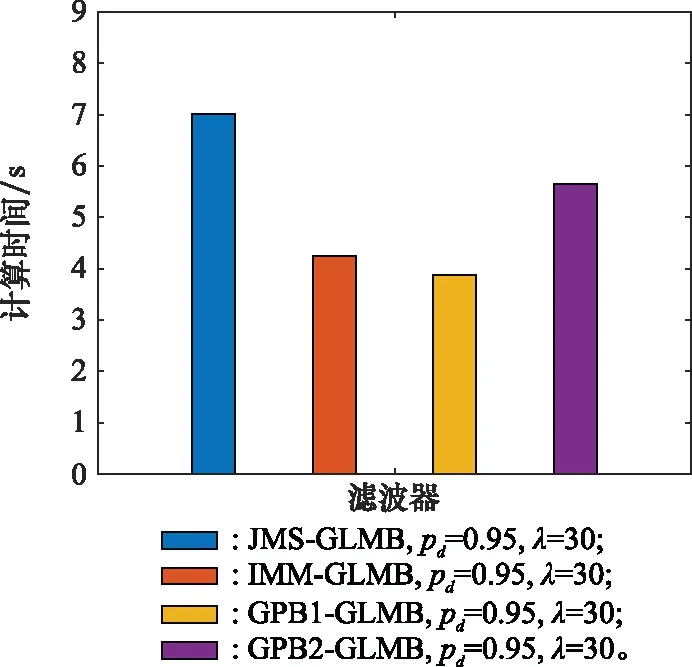
图5 4种MM-GLMB滤波器的计算时间消耗对比(λ=30)

可以看出,随着杂波率的提升,杂波造成的无效关联占用了更多的计算时间,所以4种算法的计算时间消耗差距有所缩小。

跟踪精度对比如图6所示。

图6 4种MM-GLMB滤波器的OSPA航迹跟踪 误差对比(高杂波率)

可以看出,误差距离有所抬升,所提3种算法的跟踪精度仍然都优于JMS-GLMB,其中GPB2-GLMB精度最高。

下面设置杂波率λ=5,探测概率pd=0.75,进行150次蒙特卡罗实验对比测试。4种算法的计算时间对比如表4和图7所示。

表4 4种MM-GLMB滤波器的平均计算时间对比(pd=0.75)

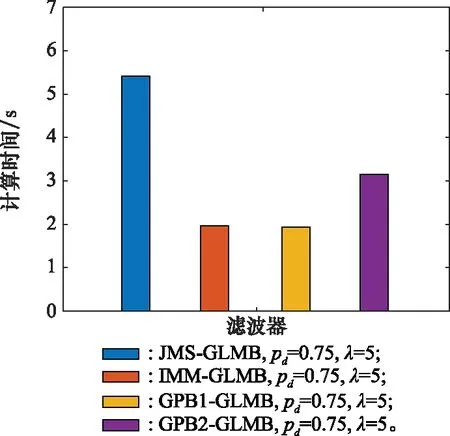
图7 4种MM-GLMB滤波器的计算时间消耗对比(pd=0.75)

跟踪精度对比的结果如图8所示,可以看出在低探测概率的情况下4种滤波器的跟踪精度与高探测概率情况相比都有较大程度的下降。

图8 4种MM-GLMB滤波器的OSPA航迹跟踪 误差对比(低探测概率)

4种滤波器的TOSPA误差对比如表5所示,可以看出JMS-GLMB精度是最低的,跟踪精度最高的是GPB2-GLMB,其次是IMM-GLMB。

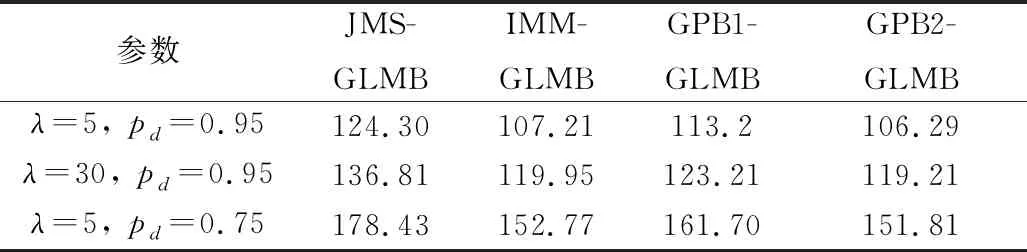
表5 航迹跟踪平均TOSPA误差对比

4种滤波器的平均目标数量估计对比如图9所示,可见4种滤波器都可以正确估计目标数量,目标数量估计性能的差距很小。

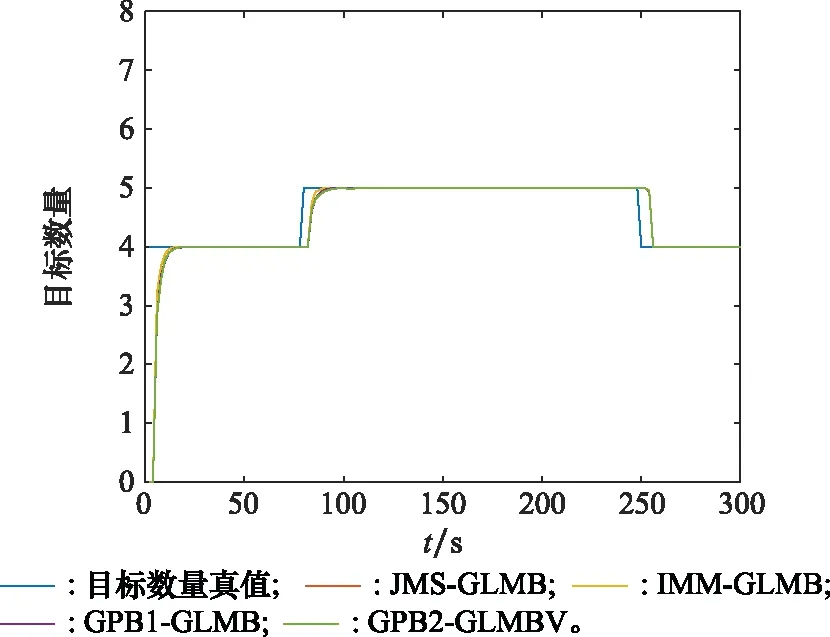
图9 平均目标数量估计对比

通过4种MM-GLMB在不同杂波率和不同探测概率下的对比可以看出:

(1) 所提3种滤波器的计算时间消耗都小于JMS-GLMB。

(2) 所提3种滤波器的跟踪精度都优于JMS-GLMB。

(3) 高杂波率和低探测概率都会增加IMM-GLMB滤波器的航迹跟踪误差,低探测概率的影响比高杂波率更显著。

(4) GPB2-GLMB的跟踪精度最高,IMM-GLMB虽然精度稍低但是计算时间与GPB1-GLMB基本一样,与GPB2-GLMB相比在计算实时性上有较大优势。

6 结 论

为了解决机动多目标跟踪问题,本文将马尔可夫分支合并策略与GLMB滤波器相结合,给出了3种MM-GLMB滤波器,包括IMM-GLMB、GPB1-GLMB和GPB2-GLMB的递推公式和高斯混合实现,并将这3种滤波器与JMS-GLMB滤波器进行对比。仿真结果表明:在计算时间消耗方面,所提3种滤波器都比JMS-GLMB有明显降低,其中GPB1-GLMB计算时间消耗最低。而在航迹跟踪精度方面,所提3种滤波器的跟踪精度也都优于JMS-GLMB,其中GPB2-GLMB跟踪精度最高。IMM-GLMB虽然计算时间和跟踪精度都不是最好的,但是在计算时间和跟踪精度上与第一名的差距都非常小,综合性能最优。因此,在航迹跟踪精度要求较高且计算资源充足的系统中可以采用GPB2-GLMB,以获得更高的航迹跟踪精度,而在计算资源紧张或目标规模较大的场景中可以采用IMM-GLMB,以非常小的跟踪精度代价换取更高的目标处理容量。