基于混合遗传算法的多箱型三维装箱问题研究
周丽,杨江龙,赵俊辉,柳虎威,2,王繁
(1.北京物资学院 信息学院,北京 101149;2.首都经济贸易大学 管理工程学院,北京 100070)
在电商仓储领域中,物品装箱操作速度高度依赖工作人员的经验和熟练程度,新手装箱的速度非常缓慢,且装箱方案的空间利用率往往较低,导致成本增加。同时,电商仓储领域也面临“无人仓”与“智能化”的转型趋势,有待突破“人工速度慢,装箱效率低”的瓶颈。因此研究自动化装箱场景下所需的装箱方案,设计电商仓储领域实际有效的智能装箱算法,提升装箱工作效率就迫在眉睫。
以维度划分装箱问题是非常常见的一种研究分类方式,主要包括一维装箱问题[1-2]、二维装箱问题[3-4]和三维装箱问题( 3D Bin Packing Problems,3D-BPP)。
关于二维装箱问题(又称“二维下料问题”)的研究非常丰富,不论是二维铡刀式背包包装问题[5],还是带切刀约束的二维带材包装问题[6],都要求一组物品必须在不重叠的情况下被打包到一个二维的箱子中[7-8]。根据物品形状不同,二维装箱问题又可以具体分为规则物品二维装箱[5,9]和不规则物品二维装箱。关于二维不规则物品装箱问题(Two-Dimensional Irregular Packing Problem, 2DIBPP)的研究,有的涉及到下料问题,要切割的小块具有不规则形状[10];有的涉及到条形包装问题,需要在一个矩形物体内放置一组多边形[11];还有的研究涉及开放维度的不规则物品二维装箱问题[12],非凸不规则物品的二维装箱问题[13-14],以及均匀多箱不规则物品的二维装箱问题[15]。
三维装箱问题是经典的一维和二维装箱问题的自然推广,很多研究将三维装箱问题转化为二维装箱问题进行求解[16]。近年来,在这一问题上的研究和出版物迅速增长[17]。其中,3D-BPP 进一步又可以分为规则物品的装箱问题、不规则物品的装箱问题。规则物品的装箱问题根据物品和箱子类型多少以及形状大小的差异,又可分为同构装箱问题(Identical 3D-BPP)和异构装箱问题(Heterogeneous 3D-BPP),与物品分类已经引入的问题类别相似,将箱子划分为相同箱子(identical large objects)、弱异构箱子(weakly heterogeneous large objects)和强异构箱子(strongly heterogeneous large objects)。其中,“同构”是指箱子或物品类型单一且尺寸相同,“异构”是指箱子或物品类型多样且尺寸不同。有学者研究了单一箱型的三维装箱问题[18],也有学者研究了弱异构物品同构箱子的三维装箱问题[19]和考虑了物品强弱异构的不同情况[20]。
在结合实际情况进行三维装箱的研究方面,有学者研究了三维切割和包装问题,强制执行非重叠约束[21],有学者研究了物流平台的集装箱装载问题[22-23]。关于集装箱装载问题(Container Loading Problem,CLP),又可以细分为多集装箱装载[24]和零担装载(拼箱)[25]。集装箱装载问题[17,20],在物流规划和调度中扮演重要角色[26]。货物被包装成标准集装箱,以便于用轮船、卡车或铁路车辆运输[27],以及航空货物的三维装箱问题[28-29]。另外,多集装箱装载问题也成为研究的关注点[30-32]。
由于电商仓储领域包装箱型号与物品种类众多,远非现有研究中的个位数,且现有研究主要优化目标为箱子的空间利用率,在装箱方案计算时间上并没有很苛刻的要求,而这并不能满足电商仓储领域装箱实践环节的时间要求。综上,文中基于电商仓储领域装箱实践的具体情境,以提高订单平均装载率为主要优化目标,在兼顾计算耗时的现实条件下,构建了混合整数规划模型,并设计了启发式装箱规则,然后通过混合遗传算法来优化物品装箱方案。
1 多箱型三维装箱混合整数规划模型
1.1 模型变量假设

1.1.1 箱子型号选择

1.1.2 物品装箱位置选择

物品装载位置选择的0—1 矩阵P如下:

确定物品装载方向后,最终装入箱子时第i件物品在各个方向上的尺寸大小分别为:

1.2 装箱模型构建
1.1.3 物品装箱方向选择
一件物品在装箱时共有6 种方向可供选择,物品装箱的不同方向可以用物品在不同维度上长尺寸表示,见图2。
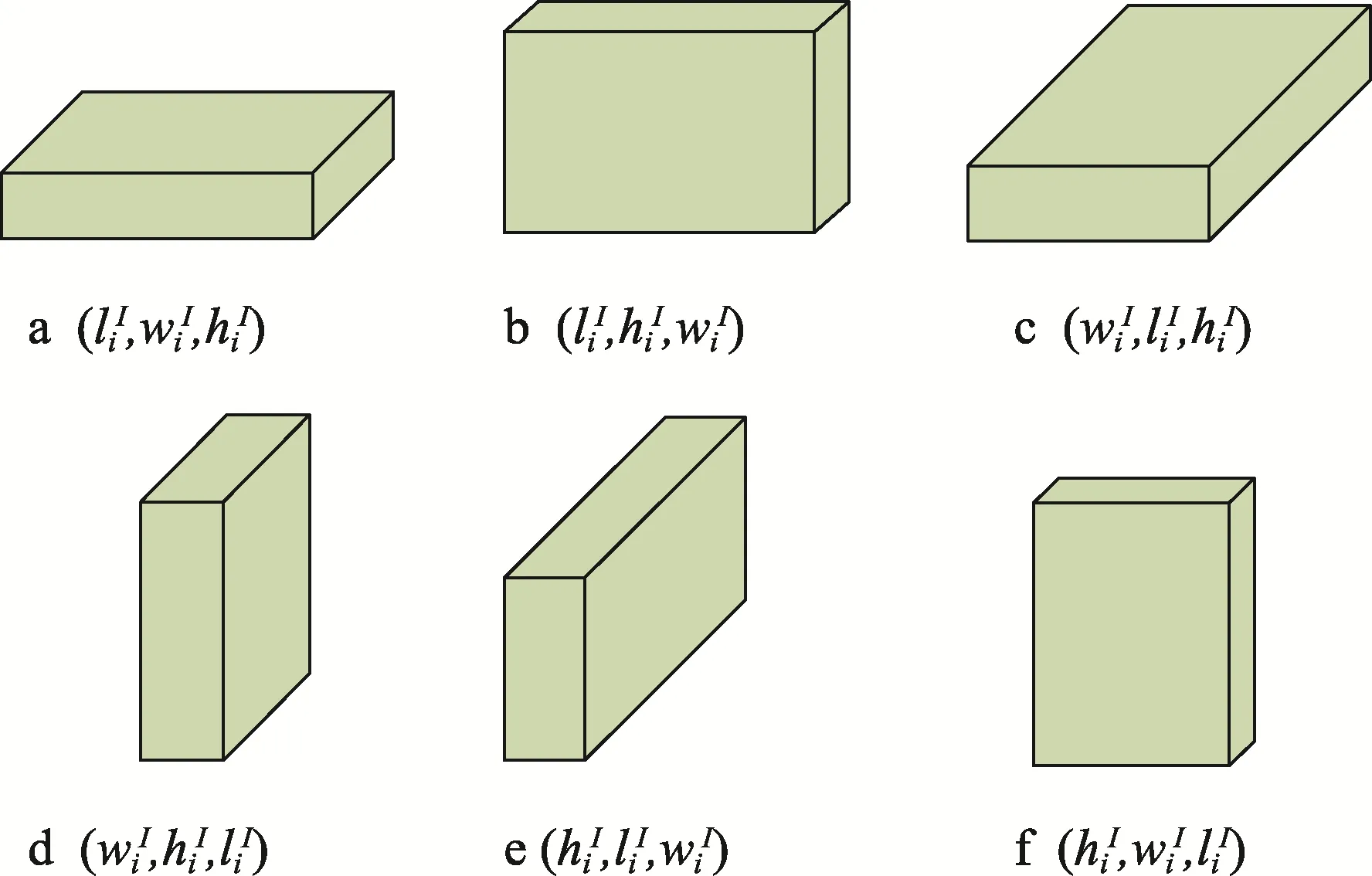
图2 物品装箱旋转方向示意图Fig.2 Schematic diagram of rotation direction of article packing
第i件物品装箱方向0—1 选择矩阵R如下。

1.2.1 模型优化目标及约束条件
从电商仓储领域的实际出发,通过分析装箱数据发现,每个订单都能被装入一个箱子中,因此,文中的问题转变为,选择一个能够装入单个订单所有物品的箱子,并使箱子的空间利用率最高。其中,物品不能超出选中箱子的空间范围,物品与物品之间不能出现空间位置的重叠。暂不考虑物品支撑、物品挤压、物品区隔等其他约束条件。
关于非越界约束,如图1 所示,只要物品的左后下角和右前上角空间坐标,即在x轴、y轴、z轴3个维度上的值,均在箱子所围成的三维空间范围内,则物品没有越界。其中,O为箱子左后下角的坐标,即原点;O*为箱子右前上角的坐标,Bi**为第i件物品在箱子三维坐标系空间中右前上角的坐标。

图1 箱子及物品装箱空间位置示意图Fig.1 Schematic diagram of space location of boxes and articles


图3 物品非重叠情况示意图Fig.3 Schematic diagram of non-overlapping items
1.2.2 装箱模型构建
以订单物品装箱的剩余空间最小为优化目标,构建混合整数规划模型如下。
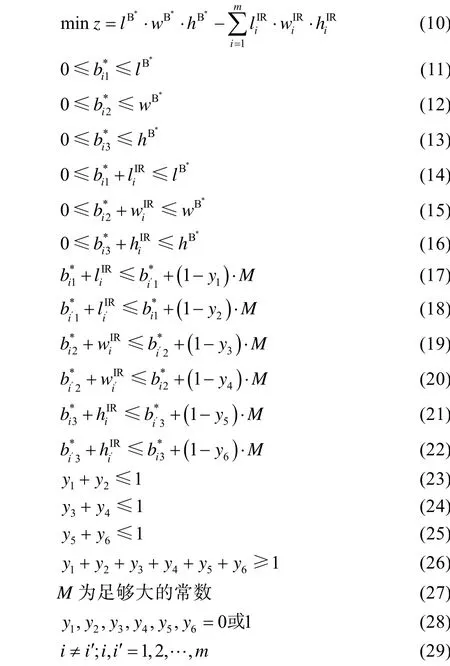
其中,式(10)为模型的目标函数,优化目标为订单装入箱子后,使剩余空间最小;式(11)至(13)为装入箱子中每件物品的左后下角坐标在箱子尺寸所允许的范围内,式(14)至(16)为箱子中每件物品的右前上角坐标在箱子尺寸所允许的空间范围内;式(17)至(25)分别为2 件物品在x轴、y轴、z轴维度上所占据区间之间的关系,式(26)保证2 件物品之间不存在空间重叠;式(27)至(29)规定了各个变量的取值范围。
2 多箱型三维装箱启发式算法设计
2.1 装箱过程模块启发式算子设计
本文设计了经验模拟算法(Empirical Simulation Algorithm,简称ESA),并基于物品装箱顺序选择模块和物品装箱位置选择模块对装箱方案进行优化。
物品装箱顺序选择是指每次选择即将装入箱子的SKU 及物品。物品装箱顺序选择算子集合主要包括物品体积降序选择算子o1u和物品装箱顺序函数选择算子o2u(φu)。o1u的作用是将订单中的物品按照体积降序依次装入箱子。o2u(φu)是指,物品的装箱顺序由函数φu所确定,其目的是通过调整物品装箱顺序,优化物品装箱策略,提升订单装载率。

2.2 多箱型三维装箱问题启发式算法设计
2.2.1 启发式算法规则设定
电商仓储三维装箱问题启发式算法主要包括4个环节:箱子型号选择,物品装箱顺序选择,物品装箱位置选择与物品装箱方向选择。
1)箱子型号选择的启发式规则。计算每种箱子类型可容纳的体积,根据箱子容积大小从小到大排列。计算当前订单中所有物品体积总和。从容积大于等于物品体积总和的箱子中容积最小的箱子开始尝试,如果当前选中的箱子能够装入所有物品,则停止计算。否则,继续尝试超过订单物品总体积的次小箱子继续尝试。以此类推,直到找到合适的箱子为止。
2)物品装箱顺序的启发式规则。选择优先装入体积较大的物品,然后再依次装入体积较小的物品,如果在物品装箱过程中,出现有物品不能装入当前选中的箱子,则更换更大的箱子重新尝试。
3)物品装箱位置的启发式规则。物品装箱位置的选择与非越界约束和非重叠约束紧密相关。文中选择“左后下角”的启发式策略,即将在箱子空间中物品的左后下角位置坐标作为物品装载位置的参考,并从箱子本身三维空间的左后下角(即原点)开始进行装箱。
4)物品装箱方向的启发式规则。物品装载方向的确定是根据图2 中展示的6 种物品方向,依次进行物品装箱尝试。得到可行的装箱方向则停止计算,否则继续尝试剩余物品方向。如果所有的装箱方向全部进行尝试并且没有找到可行的情况,则说明当前装载位置不可行。继续尝试其他装载位置,直到找到可行的装载位置和装箱方向,停止计算。
根据上述装箱问题的启发式规则,设计多种箱型三维装箱启发式算法的整体结构框架,见图4。

图4 多种箱型三维装箱启发式算法框架图Fig.4 Framework of 3D packing heuristic algorithm for various box types.
2.2.2 装箱问题的启发式算法集合
在装箱问题过程模块化的设计思路指导下,针对电商仓储领域的多箱型三维装箱问题,结合装箱过程中各个环节的设计以及过程模块中的算子集合,构建了动态复合块装箱的S 类算法。根据物品装箱位置选择方式的不同,将动态复合块装箱的S 类算法分为ESA-SHA-S1 算 法 , ESA-SHA-S2 算 法 和ESA-SHA-S3 算法。其中,每种算法包含的基本算子集合如表1 所示。

表1 动态复合块装箱的S 类算法算子集合Tab.1 Set of S-class algorithm operators for dynamic composite block packing
3 多箱型三维装箱问题混合遗传算法
3.1 装箱顺序优化的混合遗传算法
3.1.1 装箱顺序优化的混合遗传算法基本框架设计
在动态复合块装箱的S 类算法基础上,针对物品装箱顺序选择环节进行优化,设计装箱顺序优化的混合遗传算法(Hybrid Genetic Algorithm For Packing Sequence Optimization, PSO-HGA)。该算法设计的具体内容如下。
1)设计染色体编码。本算法染色体采用实数编码,以订单中SKU 的序列作为编码对象,对物品装箱顺序进行排序。通过对SKU 序列中的元素顺序重新排列,可以得到不同的订单物品装箱顺序,以此作为本算法的单个染色体编码。
2)生成初始种群。所设计的混合遗传算法采用最常见的随机排序方法。设种群中包含的染色体的数量为g,将SKU 序列中的元素随机排序g次,得到g个元素顺序不同的染色体,从而形成初始群体。
3)确定适应度函数。该算法将订单装载率作为个体适应度,则订单装载率的计算过程为适应度函数。根据模型,适应度函数可以具体表示为f,则有:

4)进行个体评价。根据种群中染色体信息所确定的物品装箱顺序,在动态复合块装箱的S 类算法框架下,计算订单装载率,可以得到每个染色体的适应度函数值f。f越大,说明订单装载率越高,反之则订单装载率越低。
5)设计选择算子。文中设计了放大优势型轮盘赌(Enlarge Advantage Roulette,EAR)算子,即在对群体适应度的值进行调整的基础上,然后再使用轮盘赌的方式筛选优势个体。调整群体适应度的规则是,在较小的适应度值的基础上增加一个较小的数值,在较大适应度值的基础上增加一个较大的数值,使得较大适应度值对应的个体有更大的概率被选中。
6)设计交叉算子。文中设计了“单点交叉,双位交换”(Single Point Crossing and Double Bit Switching,SPCDBS)算子。首先,将群体中的染色体随机分成数量相同的两组;其次,然后从每组中随机取出1 条染色体组成一个染色体对;最后,以一定的交叉概率,对取出的染色体对进行交叉操作,得到2 条新的染色体,见图5。

图5 SPCDBS 算子染色体交叉机制示意图Fig.5 SPCDBS schematic diagram of operator chromosome crossover mechanism
7)设计变异算子。文中设计了“单点变异,随机顺序”(Single point variation and sequential random,简称SPVSR)算子,即从种群中依次提取每个染色体,以一定的变异概率对取出的染色体进行变异操作。染色体变异机制见图6。

图6 SPVSR 算子染色体变异机制Fig.6 SPVSR schematic diagram of operator chromosome variation mechanism
8)迭代终止条件。该模型求解的终止条件综合考虑最大迭代次数(T)与订单装箱方案平均计算耗时2个因素,以优化订单装载率为主要目标,适当放宽计算耗时方面的要求。在订单物品装箱方案计算耗时为分钟级的时间内,确定最大迭代次数作为终止条件。
3.1.2 动态复合块装箱的PSO-HGA 算法
结合动态复合块装箱的S 类算法中各个算法的基本算子,可以进一步构建PSO-HGA 算法系列,具体包括:PSO-HGA-S1 算法、PSO-HGA-S2 算法和PSO-HGA-S3 算法。
其中,PSO-HGA-S1 算法是以ESA-SHA-S1 算法为基础,用o2u(φu)代替o1u,将混合遗传算法作为φu函数,根据搜索得到的物品装箱顺序,求得更优的订单装载率。PSO-HGA-S2 算法与PSO-HGA-S3 算法同理。因此,PSO-HGA 算法系列基本上继承了动态复合块装箱S 类算法的很多优点,例如计算耗时短,订单装载率高,并在适当放宽计算耗时的条件下,进一步优化提升装载率。
3.2 带有改进算子的混合遗传算法
3.2.1 初始群体优选的混合遗传算法
初始群体优选的混合遗传算法(Hybrid genetic algorithm for initial population optimization,简称IPO-HGA),主要是基于PSO-HGA 算法框架,针对其中“生成初始种群”的环节,不再是采用随机策略生成初始种群,而是根据o1u的规则,按照物品SKU 的体积进行从大到小排序,从而得到染色体信息。将该条由启发式规则得到的染色体信息复制g次,生成初始群体。
3.2.2 带邻域搜索算子的混合遗传算法
带邻域搜索算子的混合遗传算法(Hybrid genetic algorithm with neighborhood search operator,简称NSO-HGA),是在PSO-HGA 算法中加入邻域搜索算子NSO,以弥补其局部搜索能力的不足。如图7 所示,针对当前最优染色体的实数编码序列(Co),依次仅交换相邻2 个位置的元素所得到的新染色体集合(Cn),记为原染色体的邻域范围。计算新得到的邻域集合中所有染色体的适应度函数值,并与原有群体中的染色体合并,然后采用EAR 算子选择得到g个染色体,从而形成新的群体并应用于后续计算过程。
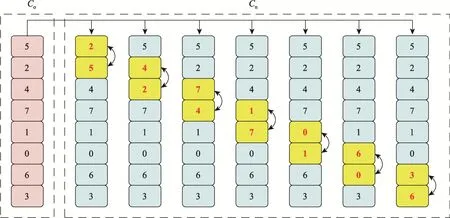
图7 原染色体与邻域染色体编码信息变换情况Fig.7 Transformation of coding information between proto chromosome and neighborhood chromosome.
3.2.3 综合多种算子的混合遗传算法
综合多种算子的混合遗传算法(Hybrid genetic algorithm integrating multiple operators , 简 称IMO-HGA),还综合了PSO-HGA 算法,IPO-HGA算法的IPO 算子和NSO-HGA 算法的NSO 算子,将改进算子作为o2u(φu)中的φu函数,其他装箱方案的计算环节不变。算法之间两两组合,得到带有改进算子的混合遗传算法系列,如表2 所示。

表2 带有改进算子的混合遗传算法系列Tab.2 Series of hybrid genetic algorithms with improved operator
4 实例验证与分析
4.1 混合遗传算法超参数确定
为了确定混合遗传算法系列的超参数设置,选择PSO-HGA-S1 算法作为典型代表,将京东企业装箱实践数据集作为测试数据,其中各种箱型包装箱尺寸信息见表3。文中的研究主要针对电商的B2B 业务领域。与个人订单相比,订单中物品的种类和数量较多,属于异构性较强的装箱问题。文中所采用的基本数据量为企业脱敏后的1 000 个订单,并在此基础上以该业务场景的订单统计特征为依据,可以生成任意数量的测试订单数据集。尝试不同的超参数组合,通过计算实验最终确定各个超参数的取值,在设定一般取值范围[33]的基础上,结果见表4。

表3 各种箱型包装箱尺寸信息Tab.3 Size information of various box types mm

表4 混合遗传算法超参数设置情况Tab.4 Super parameter setting of hybrid genetic algorithm.
由计算实验结果可知,遗传算法参数确定测试集的平均订单装载率为82.61%,订单装箱方案平均计算耗时为39.54 s。经过108 组参数组合计算实验,最终确定参数取值,如表5 所示,群体数量(M)为10,迭代次数(T)为30,交叉概率(Pc)为0.65,变异概率(Pm)为0.1。
4.2 混合遗传算法计算实验结果
4.2.1 装箱顺序优化的混合遗传算法实验结果
根据表4 得到的混合遗传算法超参数设置数值,在JD 数据集上采用PSO-HGA 算法系列进行计算实验,得到计算结果见表5。其中,PSO-HGA-S1 算法在订单平均装载率指标上表现最佳,达到了70.92%,其他算法虽然略有差距,但整体上都达到了70%以上的装载率;另外,在订单平均计算耗时方面,PSO-HGA-S1 的计算耗时最短(装载率也最低)为39.22 s,其他2 个算法的计算耗时都超过了40 s,虽然将订单装载方案计算耗时控制在了1 分钟以内,但对于计算效率要求较高的场景还是存在一定劣势。

表5 JD 数据集PSO-HGA 算法系列计算结果Tab.5 Calculation results of PSO-HGA algorithm series of JD dataset


图8 JD 数据集PSO-HGA 算法系列迭代过程Fig.8 Iterative process of PSO-HGA algorithm series of JD dataset
4.2.2 带有改进算子的混合遗传算法实验结果
在JD 数据集上采用带有改进算子的混合遗传算法计算订单实例的装箱方案,计算结果如表6 所示。其中,IPO-HGA-S1 算法的表现最佳,订单平均装载率达到了70.93%,订单平均计算耗时为40.57 s,与其他带有改进算子的混合遗传算法相比,计算耗时仅略高于IPO-HGA-S3 算法,比其他算法的计算耗时均短,并且低于PSO-HGA-S1 算法的订单平均计算耗时。在所有带改进算子的混合遗传算法中,NSO-HGA 类算法整体表现最差,订单平均装载率低于 IMO-HGA 类算法,且订单平均计算耗时高于IPO-HGA 类算法;IPO-HGA 算法虽然有较高的订单平均装载率,但是计算耗时也是最长的;IPO-HGA算法的订单平均计算耗时远低于NSO-HGA 类算法和IMO-HGA 类算法,并且IPO-HGA-S1 算法与PSO-HGA 算法系列相比,以更短的计算耗时得到了更高的订单平均装载率。
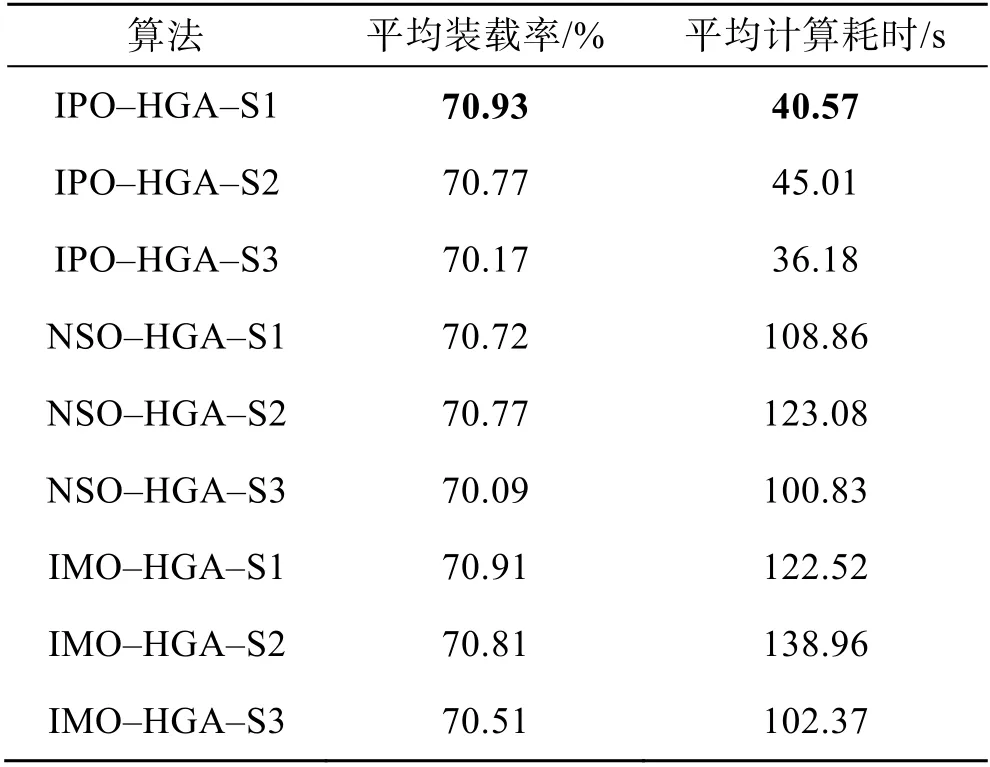
表6 JD 数据集带有改进算子的HGA 算法系列计算结果Tab.6 Calculation results of HGA algorithm series with improved operator in JD dataset

另外,NSO-HGA 类算法与IMO-HGA 算法的订单平均计算耗时均超过了 1 min , 最长的IMO-HGA-S2 算法更是达到2 min 以上,主要原因是这两类算法都采用了NSO 算子对每次迭代得到的代际最优个体进行领域搜索,根据染色体邻域搜索编码信息,NSO 算子的加入相当于使每个迭代步骤增加了 70%的个体数量,加上与 EAR、SPCDBS 以及SPVSR 之间的相互作用,因此导致计算耗时大幅增加,但是,从迭代过程与最终结果来看,相较于IPO算子,NSO 算子在提升订单平均装载率方面的作用较弱。
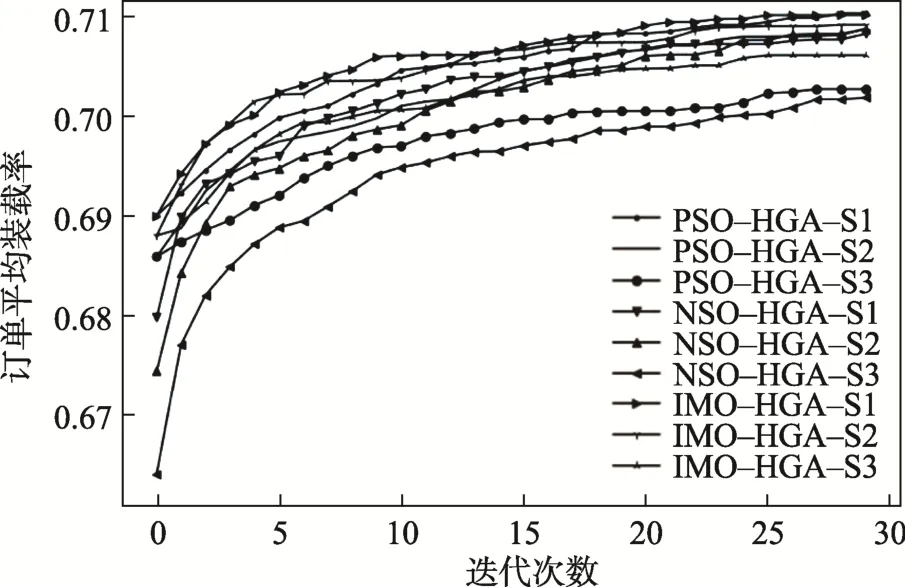
图9 JD 数据集JD 数据集带有改进算子的HGA 算法系列迭代过程Fig.9 Iterative process of HGA algorithm series with improved operator in JD dataset
5 结语
文中基于装箱问题领域已有的研究成果,结合电商仓储领域的装箱实践问题,提出了多箱型三维装箱混合整数规划模型。基于空间划分的思想与物品非重叠非越界约束设计启发式规则,针对多种箱型的三维装箱问题,设计了多种启发式算子集合与组合设计,提出装箱过程模块算法体系,保证了装箱方案的装载率与计算耗时能够满足现实需要,达到了秒级的响应速度。
文中研究还有更多可以改进的地方,例如,在算法优化方面,文中仅对过程模块算法体系中的装箱顺序算法环节进行了智能化改造,对于多个算法模块共同联合优化由于求解搜索空间过于庞大尚未涉及。后续研究可以对不同环节的算子进行算法优化,如物品装箱位置选择与物品装箱方向选择等,也可以对于多个算法模块共同联合优化。

