基于面元素重排的三维网格模型数据隐藏算法

文猛，张释如

（西安科技大学，西安 710054）

近年来数据隐藏在信号处理领域得到了广泛的应用，如所有权保护、指纹识别、身份认证和秘密通信等[1]。随着三维技术的飞速发展，以三维模型为载体的数据隐藏吸引了研究者的注意。传统的三维数据隐藏技术通过改变载体模型完成嵌入，导致载体永久失真。在医学、军事和法律取证等领域，或在某些特殊情况下，由于载体的机密性或重要性，为了避免其永久损坏[2]，三维数据隐藏不仅要能嵌入与正确提取秘密数据，还要保证载体不被修改[3]。

为了解决这个问题，Honsinger 等[4]提出可逆数据隐藏的概念，即嵌入与提取方法是可逆的，隐写模型可以通过提取秘密数据之后恢复原始载体模型。基于此，Tian 等[5]提出一种差分扩展的可逆方法，Ni等[6]提出一种直方图移位的可逆方法，这2 种方法都是针对二维图像像素值的，不能在三维模型中使用。Jhou 等[7]和Wu 等[8]用顶点坐标值替换像素值，分别将直方图移位和差分扩展应用到三维模型中，实现了三维可逆数据隐藏。文献[9-10]对上述工作进一步优化，提高了可逆数据隐藏的容量和鲁棒性。另一方面，Wen 等[11]提出零水印的概念，即不需要修改原始图像嵌入秘密数据。他们使用高阶累积量构造零水印，但只适用于二维图像。杜顺等[12]提出一种基于形状直径函数的算法，将零水印扩展到三维网格模型。在此基础上，文献[13-14]对算法进行了改进，提高了零水印的鲁棒性。

目前，保证三维数据隐藏中载体不被修改的手段有2 种：可逆数据隐藏和零水印。可逆数据隐藏能够在提取出秘密数据后恢复原始载体，零水印则强调不对载体进行任何修改，而是利用载体的某些重要特征来构造水印，但是这2 种方法都有一定的弊端，可逆数据隐藏嵌入秘密数据后会使载体失真，传输过程容易引起怀疑，安全性较低，且要恢复载体就必须先提取秘密数据，碰到顶点坐标值精度损失的情况还会提取失败，鲁棒性差；零水印用模型的某些特征生成秘密数据，用户不能自定义秘密数据大小和类型，且过于依赖知识产权（Intellectual Property Rights, IPR）信息数据库[11]，不能进行自主盲提取。针对上述问题，文中提出一种基于面元素重排的三维网格模型数据隐藏算法。根据混沌逻辑映射生成的嵌入与提取模式的对称性，联合秘密数据，可以不依赖IPR 信息数据库独立进行盲提取；无需修改顶点坐标，而是重排面元素嵌入秘密数据，兼具高安全性和大嵌入容量，且不会对载体造成任何失真。

1 无失真数据隐藏的前提

1.1 三维网格模型

三维网格模型指物体在空间中由若干个多边形连接而成，当多边形足够多足够小时，就可以完美表示物体。基础三维网格模型由点和面（大多是三角面）2 种元素构成。按一定的顺序（记作顶点的索引）排列顶点，使用顶点索引便可构成面，最后形成网格。目前主流的三维文件格式（OFF、PLY、OBJ、VRML、X3D 等）都是基于这种数据结构[15]。如图1 展示的是Bunny 三维网格模型及其局部网格情况，表1 展示了局部网格对应的数据。

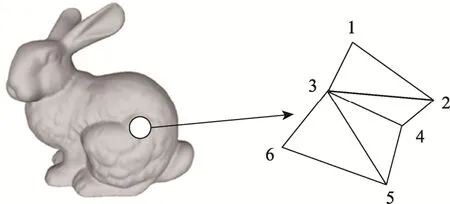
图1 Bunny 及其局部网格Fig.1 Bunny and its local mesh

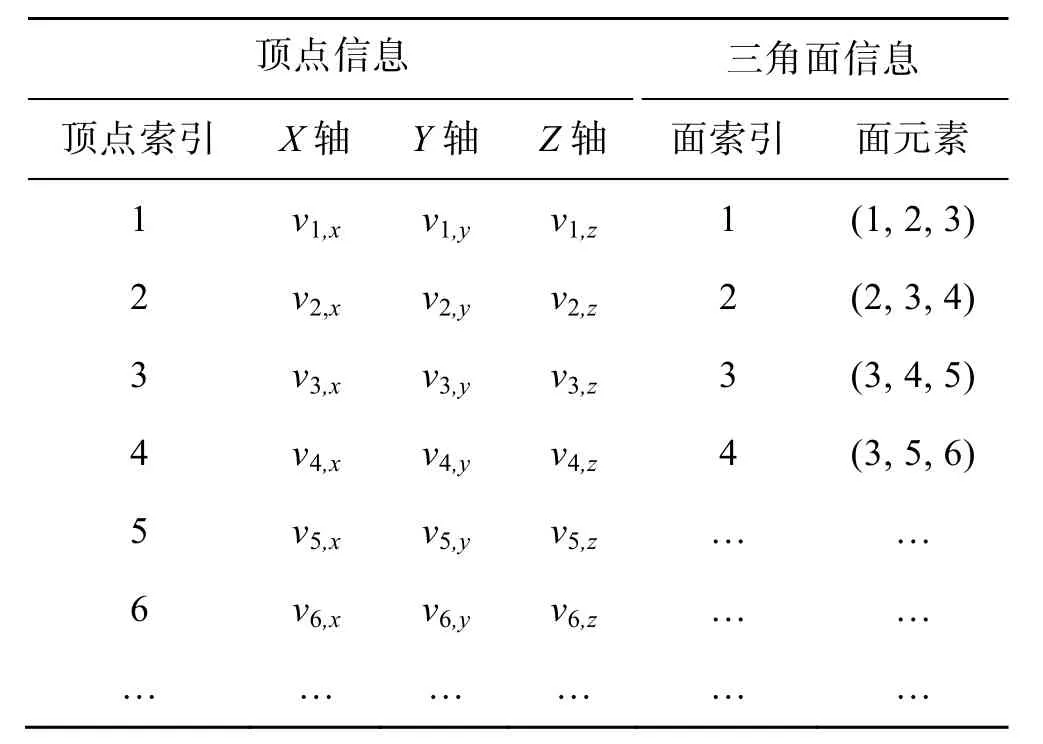
表1 局部网格文件信息Tab.1 Local mesh file information

1.2 三角面元素重排方法

传统三维数据隐藏算法通过修改三维模型顶点坐标嵌入秘密数据，易对模型造成永久失真，破坏模型，因此提出一种面元素重排的方法嵌入秘密数据。

网格中组成三角面的3 个顶点索引称为面元素，参见表1。一个三角面在空间中分两面：光照面和阴影面。依靠法线判断，法线从阴影面指向光照面，法线与面元素的关系符合右手法则，如图2 所示，当握住拳头大拇指指向法线方向时，面元素沿着指尖的方向顺序排列。

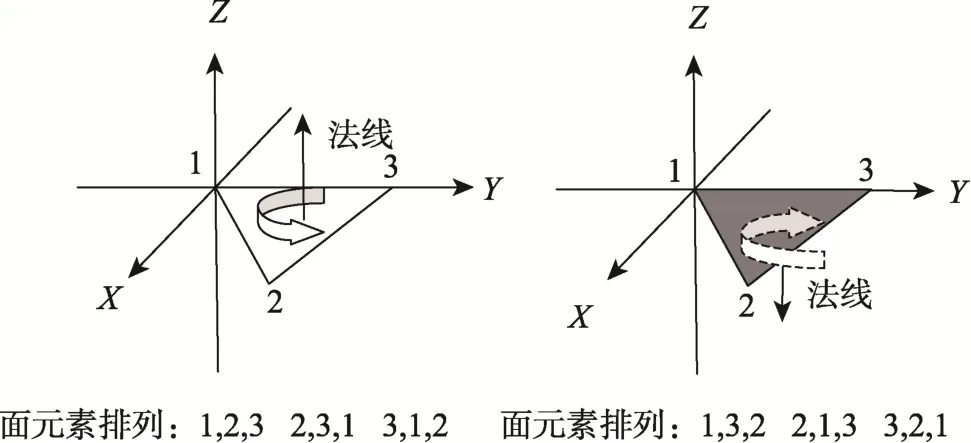
图2 右手法则Fig.2 Right hand rule

每个三角面中的3 个面元素有6 种排列方式，由于三角面在空间中的光照面朝向是确定的，为了避免三维模型失真，将三角面的排列顺序减少为3 种。在三维网格文件中，数据是以一种方式排列的，如表1所示，第1 个面的面元素是1、2、3。若用其他2 种方式表示该面元素，三维模型虽在数据保存方面有所变化，但在视觉上完全无失真。由于只是面元素的顺序交换，所以文件大小也不会改变。文中正是利用该特点，通过重排面元素的排列顺序来嵌入数据。

2 无失真数据隐藏算法

2.1 混沌逻辑映射生成模式序列

为了提高数据隐藏的安全性，使用如式（1）所示的混沌逻辑映射，在嵌入和提取数据之前先生成混沌序列[16]。

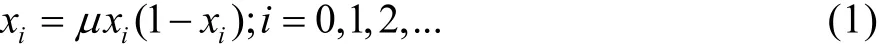
式中：xi为序列x的元素；μ为控制参数，当3.569 945＜μ≤4 时，x为混沌序列[9]。

然后通过式（2）将混沌序列x中的值乘以3，向下取整得到模式序列x'。模式序列中元素ix′的取值有3 种可能，0、1 和2，对应3 种嵌入和提取模式。

使用混沌映射具有2 个优势。一方面，秘密数据嵌入和提取之前通过混沌序列生成模式序列，随机选择嵌入和提取模式，增加了秘密数据的安全性；另一方面，通过给定相同的控制参数μ和初始值x0，得到相同的混沌序列，以此保证嵌入和提取不会出错。

2.2 嵌入过程

设有三维载体模型C，秘密数据序列I= Ii，i=0,1,2,3,…,LI，三角面F= iF，i=0,1,2,3,…,LF。LI和LF分别为I和F的长度，LI要小于LF。由于三角面的组成元素为顶点的索引，所以3 个元素不相等且有大小顺序。嵌入过程如下。

1）加载载体模型C。

2）读取iF，找出iF3 个组成元素的最小值s、中间值m和最大值l。

3）根据模式序列x′的元素值ix′确定嵌入模式。如果ix′为0，选择S 模式——iF的第1 个元素不能为s；如果ix′为1，选择M 模式——iF的第1 个元素不能为m；如果ix′为2，选择L 模式——iF的第1 个元素不能为l。

4）嵌入秘密数据序列I中的元素Ii。S 模式中，Ii为0 则Fi的第1 个元素为较小值m，为1 则Fi的第1 个元素为较大值l；M 模式中，Ii为0 则Fi的第1个元素为较小值s，为1 则Fi的第1 个元素为较大值l；L 模式中，Ii为0 则Fi的第1 个元素为较小值s，为1 则Fi的第1 个元素为较大值m。

5）i=i+1，如果i=LI则嵌入结束，得到三维隐写模型C′，否则回到步骤2。

下面举例详细说明，假设μ为4，0x为0.4，那么模式序列x'={1, 2, 0, 1,…}。设秘密数据序列I={0,1, 1, 0,……}，现有4 个三角面（表1）。如图3 所示，第1 个三角面元素排列为1, 2, 3，模式序列第1 个值为1，选择M 模式，面的第1 个元素m≠2，所以剩下2 种排列方式为123 和312。秘密数据序列第1 个值为0，所以面的第1 个元素选择较小值m=1，嵌入数据后的面元素排列为123。同理可重新排列另外3 个三角面的面元素。

图3 秘密数据嵌入过程Fig.3 Process of embedding secret data

2.3 提取过程

提取之前，需要通过参数μ和初始值0x得到模式序列x'，然后选择提取模式。提取过程如以下。

1）加载隐写模型C′。

2）读取隐写模型三角面iF′，找出iF′ 3 个组成元素的最小值s、中间值m和最大值l。

3）根据模式序列x′的元素值ix′确定提取模式。如果ix′取0，选择S 模式；如果ix′取1，选择M 模式，如果ix′取2，选择L 模式。

4）提取秘密数据Ii′。S 模式中，iF′的第1 个元素为m则Ii′为0，为l则Ii′为1；M 模式中，iF′的第1 个元素为s则Ii′为0，为l则Ii′为1；L 模式中，iF′的第1 个元素为s则Ii′为0，为m则Ii′为1。

5）i=i+1，如果i=LI则提取结束，得到秘密数据序列，否则返回步骤2。

如图4 所示，第1 个面元素排列为1, 2, 3，模式序列第1 个值为1，选择M 模式，面的第1 个元素为1，是s，所以第1 个秘密数据为0。同理可提取剩下的秘密数据。

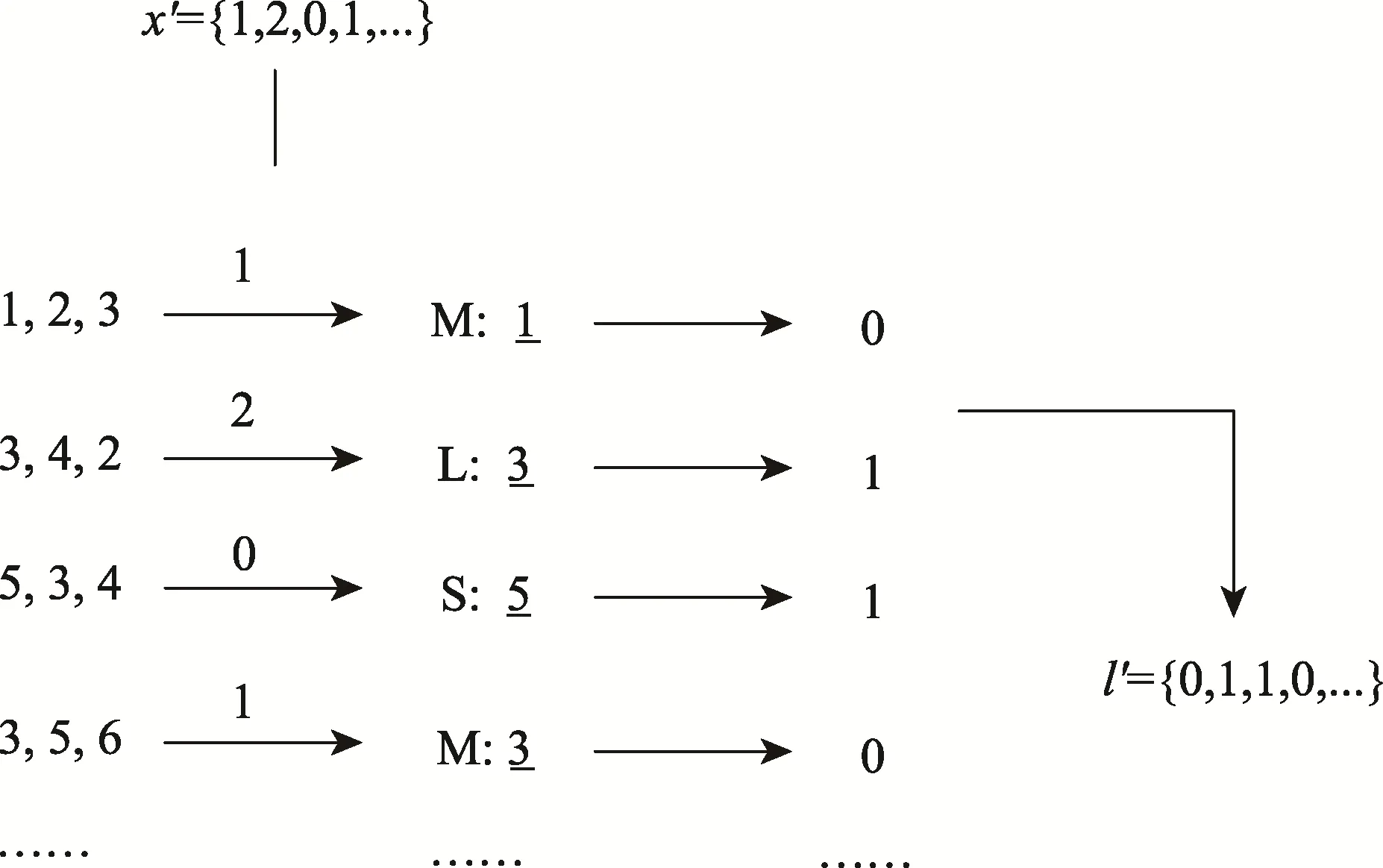
图4 秘密数据提取过程Fig.4 Process of extracting secret data

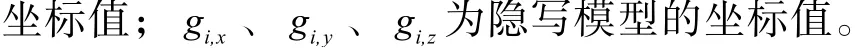
NHD 从2 个点集最大不匹配度反向衡量算法的不可见性，由网格模型包围盒的对角线长度除以豪斯多夫距离得到，豪斯多夫距离计算见式（4）。NHD接近10-4的值表示在视觉上可以接受的失真[9]。

3 实验结果与分析

实验在Pycharm2020、Meshlab、MeshMixer 环境中进行，采用斯坦福大学3D 模型库[17]中的Bunny、Dragon 和Armadillo 作为载体，见图5。

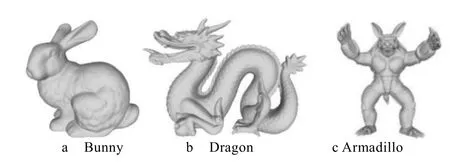
图5 3D 模型Fig.5 3D model

3.1 不可感知性

不可感知性的衡量标准有信噪比（signal-to-noise ratio，SNR）和归一化豪斯多夫距离（Normalised Hausdorff Distance，NHD）。SNR 是衡量隐写模型与载体模型失真程度的1 个参数，计算公式为[18]：

表2 对比了文中算法与其他算法在不同载体模型上的不可见性。可以看出，文中算法与零水印的效果一样，在3 个载体模型上的SNR 都为∞，NHD 都为0。说明嵌入秘密数据后的隐写模型与原始载体模型完全一致，没有任何失真。

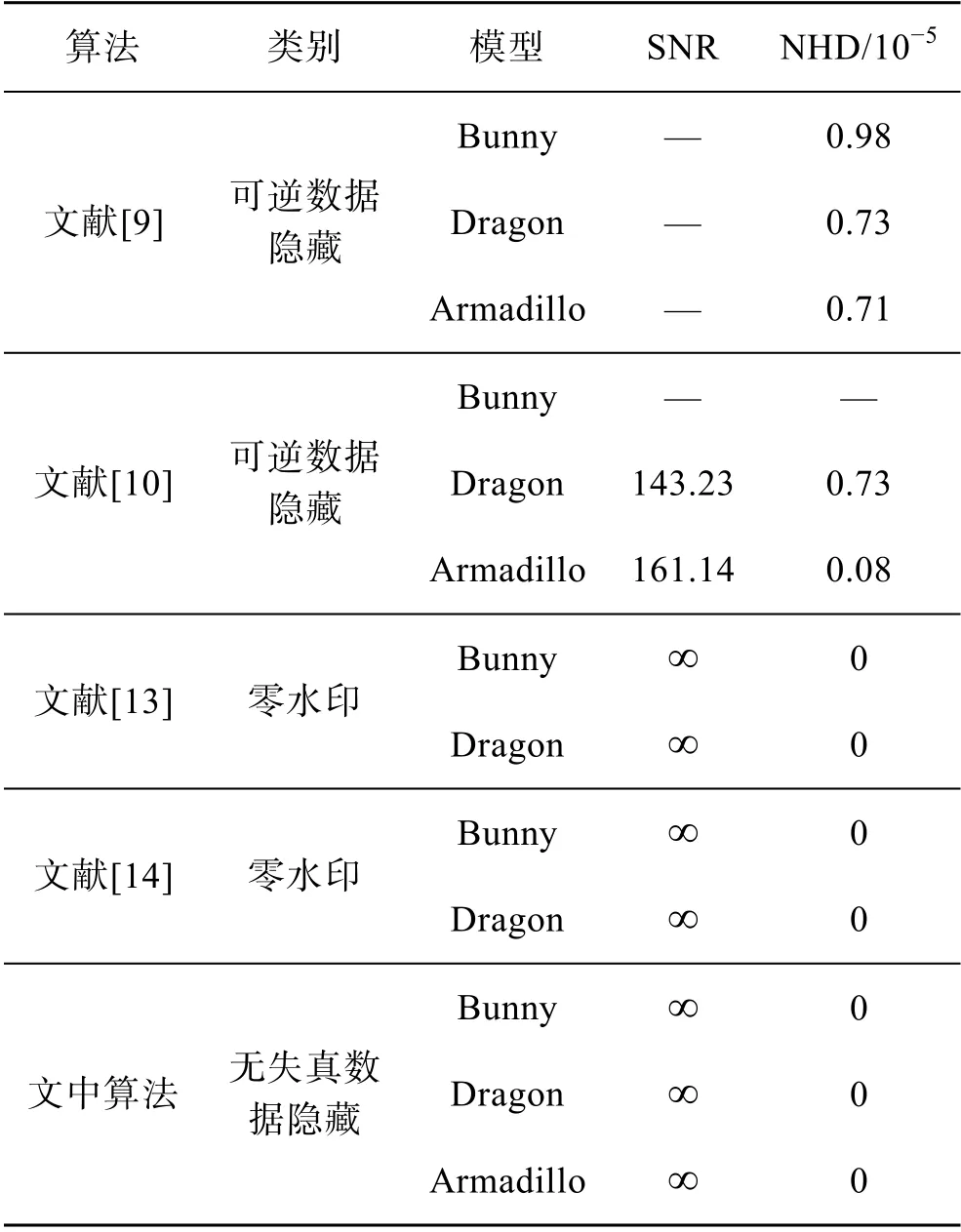
表2 不可见性对比Tab.2 Contrast of invisibility

3.2 嵌入容量

文中算法通过重新排列面元素的顺序来嵌入数据，一个面可以嵌入1bit 秘密数据。由欧拉公式（6）可知简单非空心多面体的面、边以及顶点的数量关系[19]。其中，V、E、F分别是简单非空心多面体的顶点数、边数和面数。

假设一个三角形流形网格包含足够多的边和三角形。此外，假设边界边的数量与非边界边的数量之比可以忽略，边数可以由式（7）近似得到[20]。

当顶点数量足够多时，文中算法的嵌入容量近似为2 比特每顶点（Bit Per Vertex，BPV）。

3.3 鲁棒性

文中算法通过重排面元素隐藏秘密数据，没有修改顶点，因此可以抵抗针对顶点的攻击，如噪声攻击、平滑攻击和平移、旋转、缩放等仿射变换攻击。

为了验证文中算法，采用错误比特率（Bit Error Ratio, BER）和相关系数ρ[14]进行客观判断。BER 和ρ的计算分别见式（9）和式（10）。

通过MeshLab 软件和python 编程对Dragon 模型进行了多种攻击，见表3。可以看出，文中算法对于随机噪声、拉普拉斯平滑和旋转、平移、缩放等仿射变换攻击，BER 都为0，ρ都为1，说明文中算法可以完全抵抗这几种攻击。

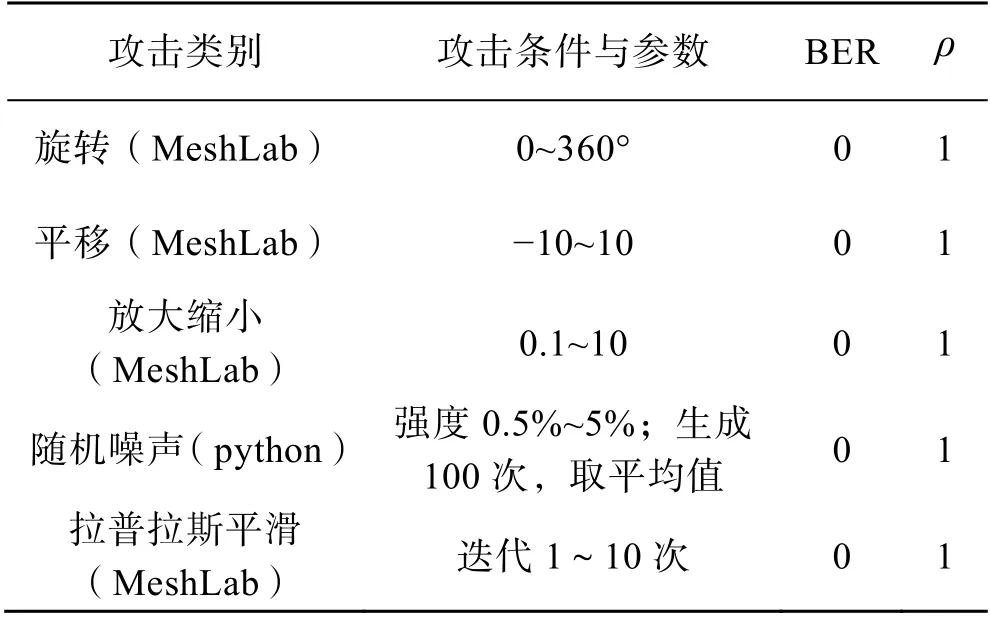
表3 不同攻击下的鲁棒性测试Tab.3 Robustness tests under different attacks

剪切攻击会减少模型的顶点和面的数目，是网格模型类算法中对嵌入的秘密数据破坏最严重的攻击[22]。剪切攻击对鲁棒性的影响和剪切比例、剪切位置和嵌入容量均有关，如果剪切部分不含秘密数据，那么提取数据的正确性不受影响。嵌入容量越大，不含密的三角面占比越小，所能完全抵抗的剪切比例越小。

为了测试对剪切含密三角面的鲁棒性，将871 414 bit秘密数据满容量嵌入Dragon 模型（含有871 414 个三角面），表4 展示了不同剪切比例下的BER 和ρ。当秘密数据嵌满Dragon 模型，剪切比例小于5%时，文中算法的ρ仍大于0.6，BER 仍小于25%，表明文中算法对剪切攻击有一定的抵抗能力。

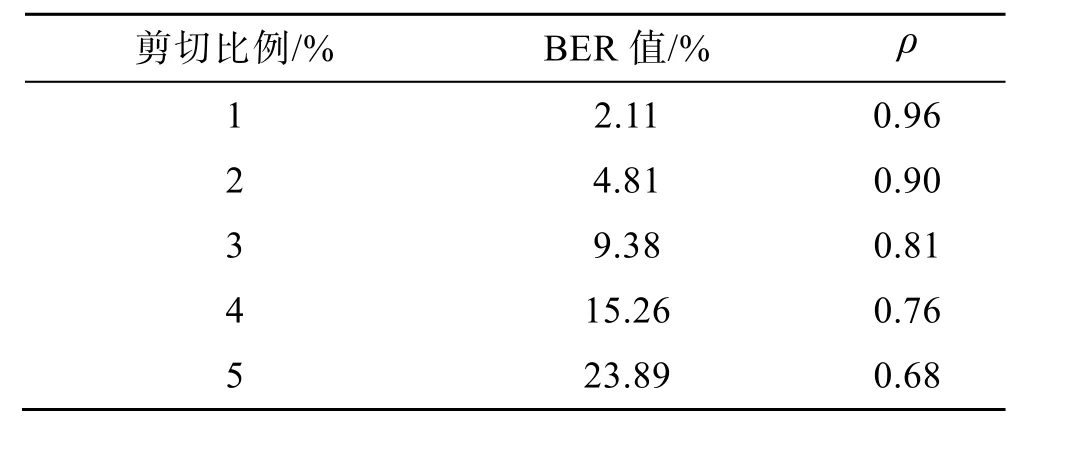
表4 满容量嵌入下不同比例剪切测试Tab.4 Cropping tests of different proportions under full capacity embedding

3.4 安全性

文中算法有2 个安全性保障：载体无失真和混沌逻辑映射选择模式。相较于传统算法，由于载体模型与隐写模型的完全一致性而不易被人发现，增加了安全性，即使被发现，若不知道参数μ和初始值0x，也无法正确提取出秘密数据。

参数的范围μ∈ （ 3.569 945,4]，x0∈ （ 0,1），此次嵌入过程取μ=4、x0=0.065。图6 展示了不同μ时，提取过程中BER 随x0取值变化的波动范围。可以看出，当μ和x0取值不正确时，提取后数据的BER 值都小于40%。实际中μ和x0的取值有无数个，说明文中算法具有较高的安全性。

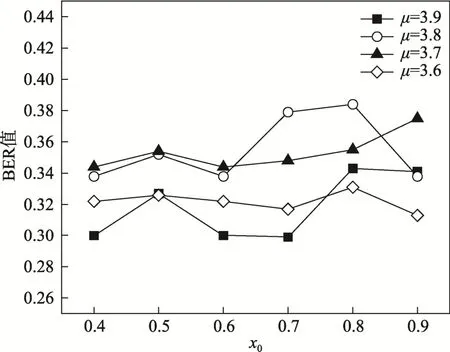
图6 嵌入模式参数对BER 的影响Fig.6 Effects of embedded pattern parameters on BER

3.5 相关工作综合比较

零水印不对载体做任何修改，可逆数据隐藏提取秘密数据后可以恢复载体。文中算法属于无失真数据隐藏，只改变面元素的排列，对载体不造成任何失真。表5 将文中算法与最新的零水印和可逆数据隐藏方法进行了比较。可以看出，文中方法兼顾了零水印的无失真和可逆数据隐藏的盲提取，嵌入容量较大，鲁棒抗性方面优于可逆数据隐藏，与零水印方法相当。

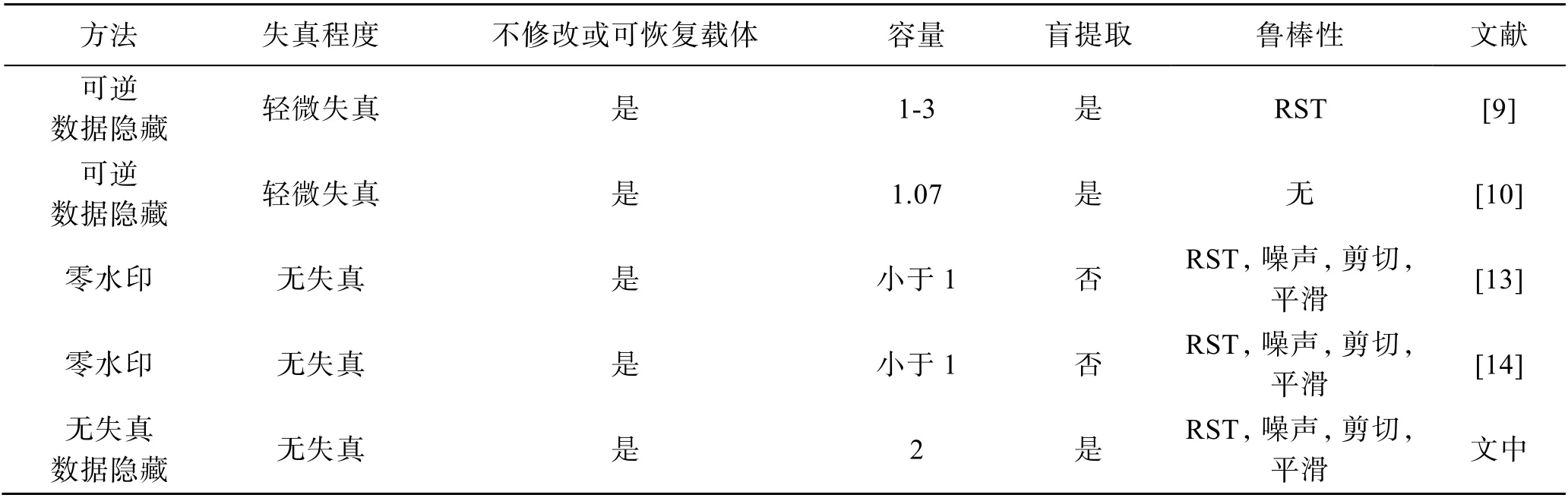
表5 三维数据隐藏算法比较Tab.5 Comparison of 3D data hiding

4 结语

文中提出了一种基于面元素重排的三维网格模型无失真数据隐藏算法，具有以下优势：这种方法做到了更加便捷的盲提取；这种方法通过重排面元素顺序隐藏秘密数据，不会对载体模型造成任何失真，可以用于载体不容修改的军事和医学领域；未修改载体模型顶点数据，所以生成的隐写模型在网上进行传输时，即使遭到仿射变换攻击和顶点平滑等攻击等，也能保证提取的秘密数据完全正确；使用参数μ和0x选择嵌入与提取模式，更具安全性，因而适用于秘密通信和版权保护等领域。

由于文中算法是空间域的，在抵抗剪切攻击方面有一定的不足，但对于较短的秘密数据可以重复嵌入到模型中，以提高对剪切攻击的抵抗性。