基于可分离字典的稀疏和低秩表示图像去噪

张雷，刘丛

（上海理工大学，上海 200093）

在图像采集、传输等过程中，由于采集设备和传感设备的影响，不可避免地会产生噪声图像。这严重影响了图像分割、图像识别等后续的图像解译工作[1]。图像质量的下降会影响人们对图像的视觉观察效果，同时后续也会阻碍对图像提取有用的信息[2]。图像去噪是一种基本的图像处理技术，其通过对噪声图像处理以恢复原始的清晰图像。该技术广泛地应用于图像处理、信号处理以及计算机视觉等诸多领域。

传统的图像去噪研究利用图像的先验信息进行去噪，如梯度模型[3]、低秩模型[4]和稀疏模型[5]。在稀疏表示去噪中，原始图像通过一个过完备字典和一组稀疏系数矩阵的线性组合映射到低维空间以去除噪声。在该模型中，每个子图像都是独立的，没有考虑到相似子图像间的相关性。针对该问题，低秩表示（LRR）[6-7]可以挖掘不同系数之间的相关性。LRR将整个图像分为多个子向量，每个子向量对应一个系数，并对系数矩阵添加低秩约束以更好地捕捉数据的全局结构。LRR 在图像去噪中获得了成功，但其自身仍存在一些问题。首先，它在去噪过程中仍然将整个图像划分为多个图像块或者向量操作，不可避免地会带来巨大的计算量。其次，该模型通常将图像自身作为字典而缺乏有效的字典表示。针对上述问题，Bahri等[8-9]采用了一种具有Kronecker 结构的低秩可分离字典（SeDiL）。一方面，低秩可分离字典可以克服LRR 中无结构良好的字典的问题，可以很好地反映整幅图像的低秩性。另一方面，在文献[8-9]中，它可以出色地完成高水平噪声下的去噪任务。针对该改进，文中进一步结合可分离字典的学习和低秩表示的优点，设计了一种高效的去噪模型以应对高强度噪声图像去噪，称为基于可分离字典的稀疏和低秩表示（SLRR-SD）。该模型首先使用可分离字典代替LRR中的过完备字典，以解决LRR 无法寻找合适字典的问题。其次，使用Frobenius 范数对2 个分离字典约束，以寻找字典内部的低秩性。进一步，受Zhang 提出的结构化低秩表示（SLRR）[10-11]的启发，为了获得更有效的表示，使用SLRR 以增加系数矩阵的稀疏性。大量的实验结果表明，提出的算法在面对高强度噪声时，获得了较好的去噪效果。

1 相关工作

1.1 低秩表示

虽然LRR 可以在一定程度上缓解SR 的行列信息丢失问题，但并没有从根本上解决这个问题。在实际操作中，图像的表示是从矩阵变为列向量。

1.2 结构化低秩表示

SLRR 是LRR 的改进模型，它在LRR 的基础上增加了稀疏表示来建立新的模型。

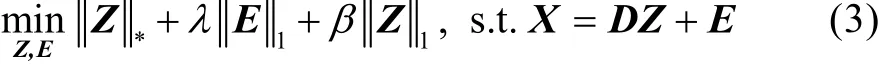
从这个新模型中可以看出，低秩分量揭示了全局信息，而稀疏性决定了图像属于哪一类[7]。此外，SLRR 还提出了一种学习字典的方法，解决了LRR没有较好结构字典的问题。与LRR 类似，SLRR 仍然不能解决数据的维度问题。

1.3 可分离字典学习

图1 基于可分离字典表示的二维数据Fig.1 Two-dimensional data based on separable dictionary representation

2 基于可分离字典的稀疏和低秩表示

此节介绍基于可分离字典的稀疏和低秩表示模型。该模型结合了SLRR 和SeDiL 的优点，能有效地去除高密度的噪声。一方面，对于模型的优化，不仅要考虑某些因素，还要考虑它们之间的相互影响。在弹性网络[12-14]中，1L和2L范数作为联合惩罚项，解决了稀疏性和稳定性之间的平衡问题。压缩感知理论表明，模型解的稀疏性和稳定性是不能同时实现的，因此在模型设计过程中应充分考虑它们之间的相互作用。基于这个思想，1L范数和核范数被结合在文中的稀疏和低秩表示模型中。1L范数控制表示系数的稀疏性，而核范数控制其低秩性，使得表示系数更稳健有效，恢复结果更好。此外，SLRR-SD 能够将整个图像表示为一个低秩矩阵以克服行和列之间信息丢失的缺点，并获得有效的全局表示。另一方面，传统的K-SVD 方法得到的字典只适用于小图像块，而不能处理大图像块甚至整幅图像。SLRR-SD 获得的Kronecker 结构的可分离字典可以很好地解决这个问题，而且可分离字典具有低秩性，图像重建能力更强。通过低秩表示和低秩分离字典，可以使恢复的图像达到理想的低秩。最后，K-SVD 方法需要通过预训练样本来学习字典，这种方法会带来沉重的计算负担，而SLRR-SD 通过在线学习字典很好地克服了这一缺陷。

2.1 模型

LRR-SD 模型见式（6）。

2.2 迭代优化

在这里，使用交替方向乘子法（ADMM）[16]来优化式（8）可得：

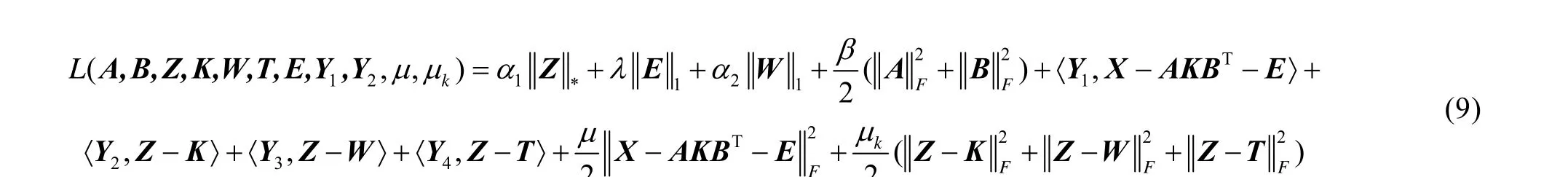
如上所述，当优化一个参数同时固定其他参数时，式（9）的损失函数是凸的。通过交替更新每个参数来优化它，直到达到收敛。

2.2.1 更新变量E

假设所有其他参数都是固定的，通过求解式（10）来更新噪声矩阵E。

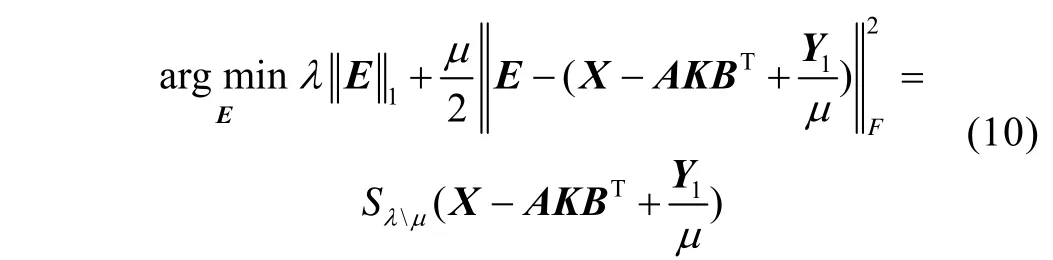
式中：S( )为软阈值收缩算子[17-18]。

2.2.2 更新变量A

假设所有其他参数都是固定的，通过求解式（11）来更新可分离字典A。

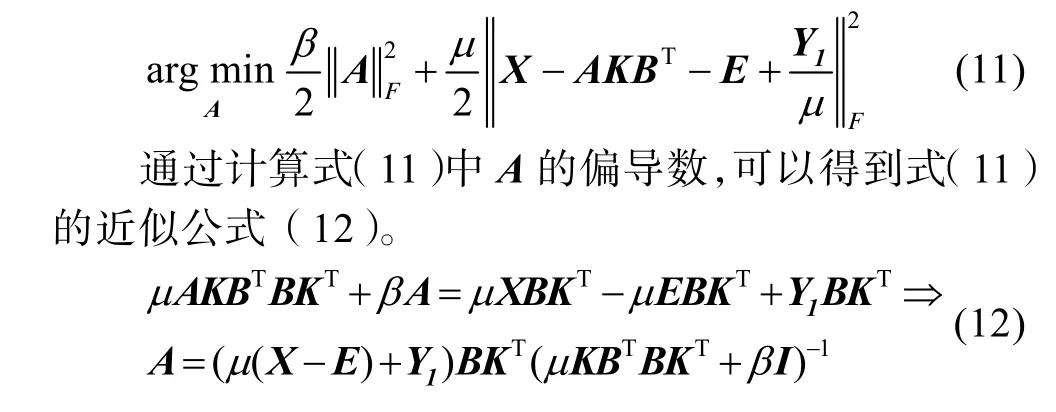
2.2.3 更新变量B

假设所有其他参数都是固定的，通过求解式（13）来更新可分离字典B。

2.2.4 更新变量K

假设所有其他参数都是固定的，通过求解式（15）来更新分离变量K。

更新式（16）中的K是一个挑战。其中式（16）是Stein 方程，可以用离散时间的Sylvester 方程求解，如Hessenberg-Schur 方法。

2.2.5 更新变量Z

假设所有其他参数都是固定的，通过求解式（17）来更新低秩表示Z。

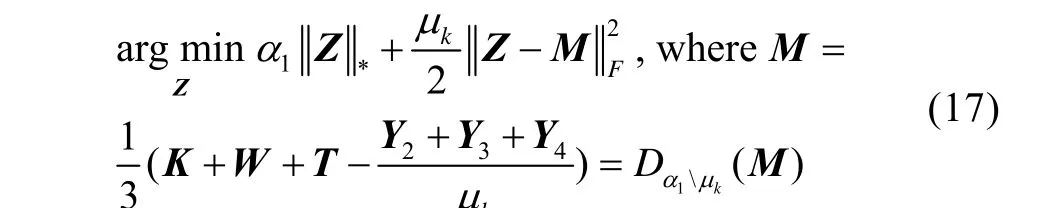
式中：D( )为奇异值收缩算子[17-18]。

2.2.6 更新变量W

固定其他的变量，通过求解式（18）来更新分离变量W。

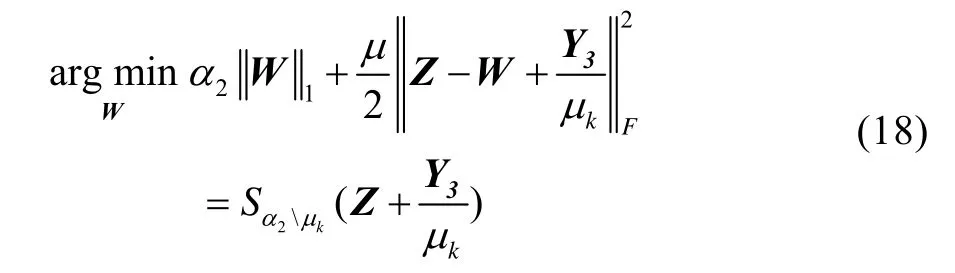
2.2.7 更新变量T

固定其他的变量，通过求解式（19）来更新分离变量T。

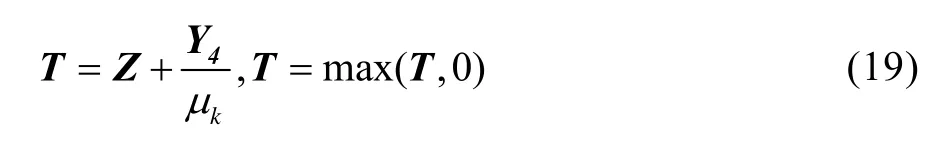
3 实验及结果分析

3.1 实验设置

3.1.1 数据集

1）基准图像，即Facade 图像[19]。这幅画具有鲜明的特征，如黑色的十字架、窗户，以及用墙纹装饰的窗户中的物体。

2）Berkeley Segmentation 数据集[20]。它由300张图像组成，用于灰度和颜色分割。

3）Set 12 数据集。该数据集包含12 幅图像处理中应用最广泛的灰度图像，如Lena、House、Parrot等。文中测试了3 个数据集中的100 多张图像，这里只应用了8 张测试图像来展示去噪结果，见图2，分别为Façade（202×194）、Flower（321×481）、Bear（481×321）、Ostrich（481×321）、Lena（128×128）、Barbara（256×256）、House（256×256）、Parrot（256×256）。

图2 测试图像Fig.2 Test images

3.1.2 对比方法

文中将2 个去噪模型与6 种相关的方法进行比较。前 3 种比较方法是基于不同的字典[21]，包括K-SVD 字典（K-SVD）、DCT 字典（DCT）和全局字典（Global）；第4 个比较方法是最小权重核范数（WNNM）[22]，其中奇异值被赋予不同的权重；第5种比较方法是稳健主成分分析（RPCA）[23]；第6 种比较方法是鲁棒非线性矩阵分解的鲁棒非线性分解方法（SNLMF）[24]。

3.1.3 参数设置

3.1.4 对比定量

峰值信噪比（PSNR）[25]可以衡量恢复图像的平滑度，而特征相似度指数（FSIM，彩色图像为FSIMc）[26]可以衡量恢复图像的特征信息。

3.2 视觉及定量对比

在 3 个数据集（Facade 图像、Berkeley Segmentation 数据集和Set 12 数据集）上的实验结果如图4 所示。在实验中使用了4 种噪声强度，噪声强度5%用于模拟低强度噪声损伤，噪声强度10%和20%用于模拟中度破坏，噪声强度30%用于模拟严重破坏。

3.2.1 基准Façade 图像

现在分析在Façade 图像上通过不同方法获得的去噪结果。在噪声强度5%、10%、20%和30%下，定量结果分别显示在表1、表2、表3 和表4 的第1列中。从表1—4 中可以看出，所提出的SLRR-SD表现出最好的性能。在表4 中，其他模型在数值上与文中算法有很大的差距。

在噪声强度10%和30%下的视觉结果如图3 和图4 的第1 行所示。从图3 中可以看出，大多数比较方法都能很好地恢复图像，噪声去除比较干净并保留了图像的大部分信息。DCT、K-SVD、Global 和WNNM得到的去噪结果严重丢失了图像的原始信息，如建筑物上的黑色十字、窗户上的物体和墙上的线条，而提出的SLRR-SD 可以更好地恢复原始信息，它保留了建筑外墙的这些特点。

3.2.2 Berkeley Segmentation 数据集

在噪声强度为5%、10%、20%和30%下，定量结果分别见表1、表2、表3 和表4 的第2、3、4 列中。从表1—4 中可以看到提出的SLRR-SD 在所有噪声强度下仍然获得了3 图像的最高测量值。在表4中，其他模型在数值上与文中法有很大的差距。

在噪声强度为10%和30%下的视觉结果如图3和图4 的第2、3、4 行所示。图3 中的大多数方法都可以很好地恢复这3 个图像的原始信息。在噪声强度为30%下，大部分比较方法都丢失了花瓣、花瓣上的线条和中心花蕊的细节。熊头部和周围杂草的轮廓已经模糊，有些甚至看不到杂草。鸵鸟的眼睛和嘴巴已经变形或以其他方式丢失，并且背景噪声也没有完全消除。这表明在高强度噪声条件下，文中算法在保留原图像信息的同时能够很好地完成去噪任务。

图4 噪声强度为30%的去噪结果Fig.4 Denoising results for 30% noise intensity

3.2.3 Set 12 数据集

在噪声强度为5%、10%、20%和30%下，定量结果分别显示在表1、表2、表3 和表4 的第1、2、3、4 列中。提出的SLRR-SD 在所有表中的值依然是最高的。

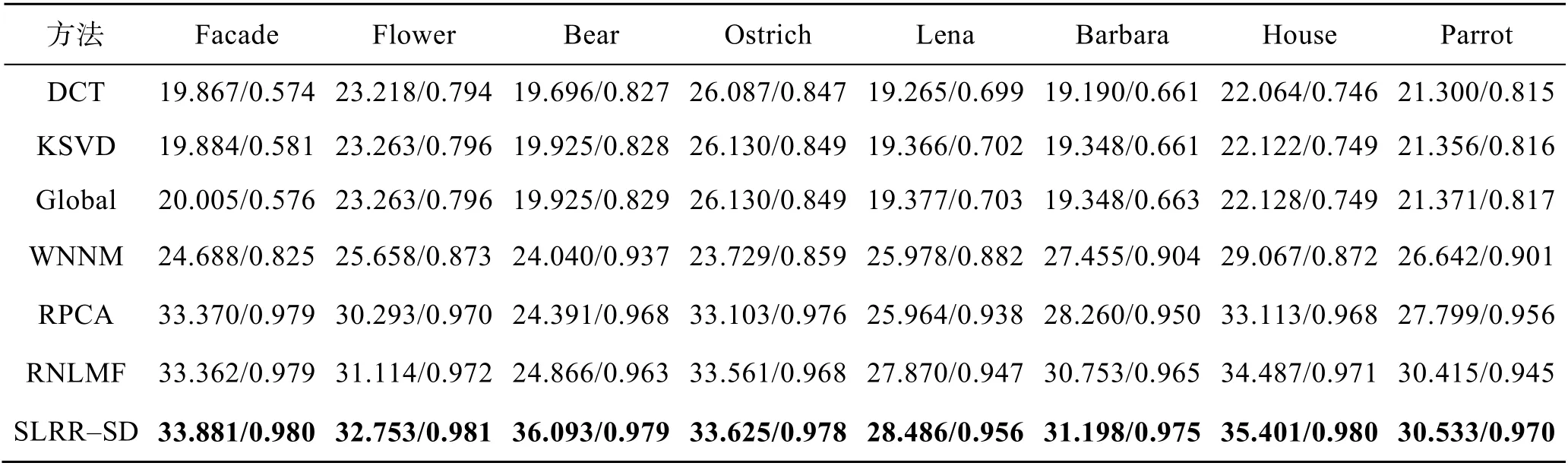
表1 噪声强度为5%的PSNR/FSIM 值Tab.1 Values of PSNR/FSIM for 5% noise intensity

表2 噪声强度为10%的PSNR/FSIM 值Tab.2 Values of PSNR/FSIM for 10% noise intensity

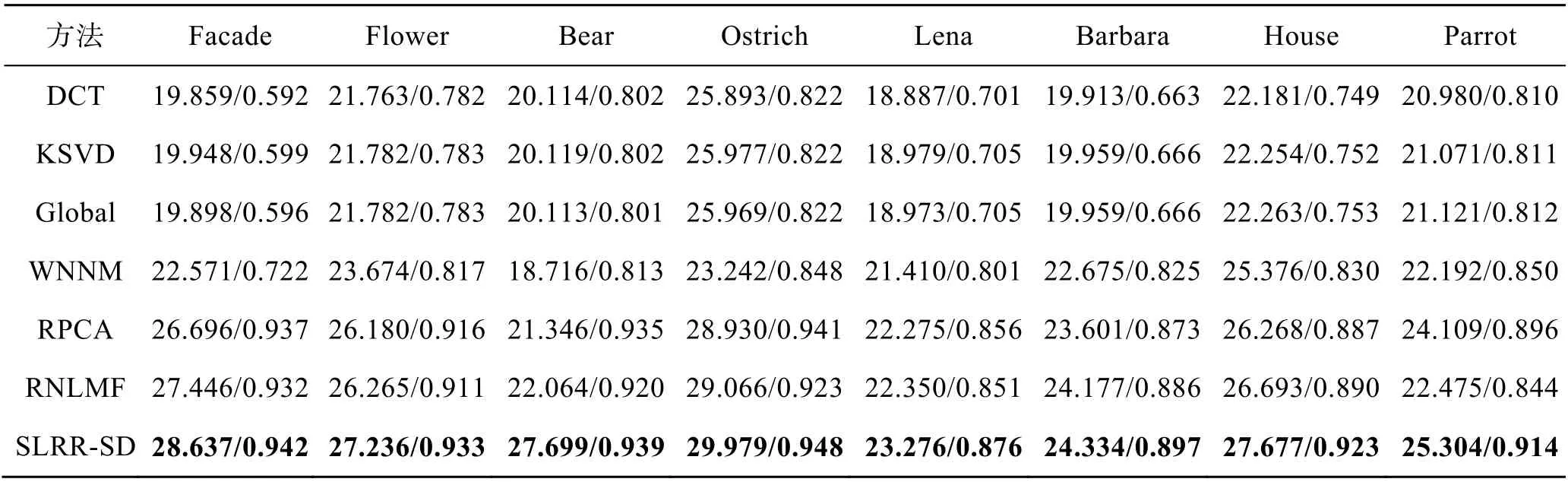
表3 噪声强度为20%的PSNR/FSIM 值Tab.3 Values of PSNR/FSIM for 20% noise intensity

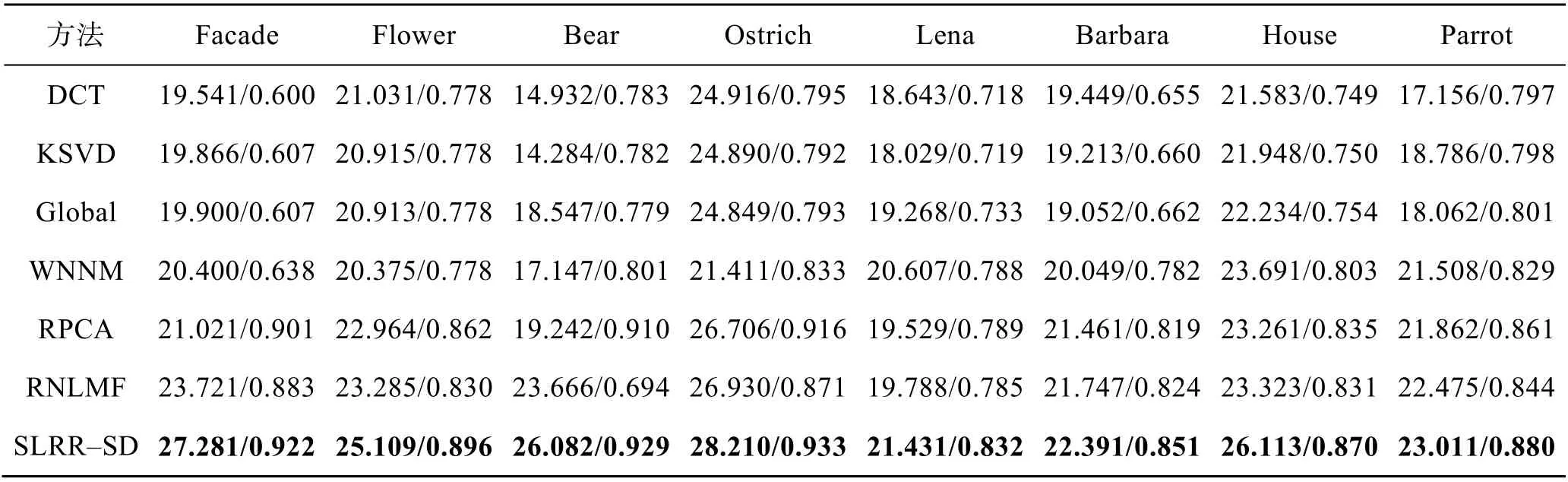
表4 噪声强度为30%的PSNR/FSIM 值Tab.4 Values of PSNR/FSIM for 30% noise intensity

在噪声强度10%和30%下的视觉结果如图3 和图4的第5、6、7、8 行所示。在噪声强度30%下，该数据集中数值与视觉的对比更加明显。首先，在图4 中，大多数方法的Lena 和Barbara 人物的面部轮廓、头发、帽子和围巾完全看不清楚。此外，House 和Parrot 几乎看不到图像的轮廓，细节信息完全丢失。SLRR-SD 不仅可以保留大致的轮廓结构，还可以恢复一些原始细节，例如Lena 的面部结构和Parrot 的纹理信息。

3.3 收敛分析

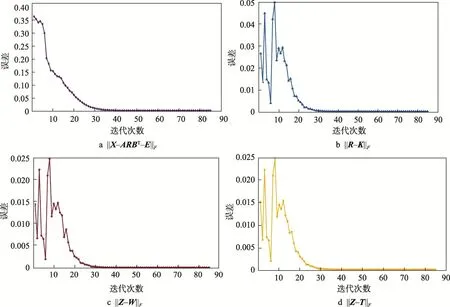
图5 迭代误差Fig.5 Error of iteration

4 结语

文中提出了基于可分离字典的稀疏和低秩表示算法用于图像去噪。在SLRR-SD 中，低秩表示和低秩可分离字典用来提升整幅图像的低秩性。将稀疏表示与低秩表示相结合，以获得更有效的表示，进一步增加了整幅图像的低秩性。此外SLRR-SD 不仅能保留相邻列之间的相关性，并且它的可分离字典优化过程也降低了计算负担。提出的算法在噪声强度5%、10%、20%和30%下的PSNR/FSIM 的平均值分别为32.736/0.975、29.769/0.957、29.295/0.951 和26.768/0.921。仿真实验结果表明，提出的模型不仅可以消除噪声，而且可以恢复更多的图像特征信息，并且在高强度噪声的破坏下SLRR-SD 依然可以获得良好的恢复效果。在未来的工作中，将继续深入研究图像去噪领域，探索高维度、高规模的图像去噪技术。