离散奇异随机Markov跳变系统Stackelberg博弈及其应用
周海英,罗震东,周 艳
(1.广州航海学院港口与航运管理学院,广东 广州 510725;2.广东工业大学管理学院,广东 广州 510630)
Markov跳变系统在制造系统、飞行控制器系统、机器人操作系统、通信系统、神经网络中的分析仿真等都有着非常实际的应用背景[1-2],近几十年来,国内外学者针对Markov跳变系统开展了大量研究,成果丰富,如Markov跳变系统的随机稳定性和H∞控制[3-4],Markov跳变系统的随机线性二次最优控制[5-8],Markov跳变系统的混合H2/H∞控制[9-10]等。与Markov跳变系统相比,奇异Markov跳变系统更适合于描述动态系统的结构特征,能更好的刻画现实中由随机突变现象引起系统跳变的情形,如工程领域和金融领域的期权定价问题,投资型保险红利分发问题等,因而,奇异Markov跳变系统近年来得到国内外学者的广泛关注,Tao等[11]利用滑动模控制方法研究了具有时变时滞的奇异Markov跳变系统的随机容许性问题,Guerrero等[12]探讨了具有部分已知转移概率的Markov跳变线性奇异系统(mjlss)的随机稳定性问题,Yin等[13]研究了转移概率部分未知的奇异Markov跳变系统的鲁棒故障检测问题。
随着社会经济和博弈理论的发展,不少学者将博弈理论用于研究描述现实问题的奇异随机系统,取得了一系列研究成果,如奇异随机系统的鞍点均衡策略[14]和线性随机系统的Pareto最优策略[15],随机Markov跳变系统的Nash均衡策略[16-17],奇异随机Markov跳变系统的N人Nash均衡策略[18-19]等。笔者通过文献调研,发现目前关于奇异随机Markov跳变系统Stackelberg博弈的文献成果还较少见报。
基于此,本文讨论有限时间和无限时间情形下的离散随机奇异Markov跳变系统的Stackelberg博弈问题,并将所得结果应用于相应的随机H2/H∞鲁棒控制问题,丰富随机奇异Markov跳变系统微分博弈理论及应用研究。
1 预备知识
给定T>0表示一个有限时刻,为了叙述方便,引入下述符号:
A′:矩阵或向量A的转置;
Sn:全体n×n阶对称矩阵构成的集合;
C(0,T;n×m):全体连续函数φ:[0,T]→n×m构成的集合;

L∞(0,T;n):一致有界函数f(·):[0,T]→n构成的全体;
χA:集合A的指示函数。
设在给定的完备概率空间(Ω,F,{F}t≥0,ρ)上,其上定义了一个自然滤子{F}t≥0,ε(·)表示对应概率测度的数学期望。在概率空间上,定义一维标准Wiener过程{w(t)}t≥0和一个取值于状态空间Ξ={1,2,…,l}的Markov过程{rt}t≥0,且{rt}和{w(t)}相互独立。Markov过程的转移概率如式(1):
πij=P(rt+1=j|rt=i),∀i,j∈Ξ
(1)

考虑式(2)所示It型离散奇异随机Markov跳变系统:
(2)
其中,x(t)∈n是状态变量,(x0,r0)∈n×Ξ是初始状态,E∈n×n,是给定的奇异矩阵,rank(E) 引理1对所有的i∈Ξ,如果存在一对非奇异矩阵M(t,i)∈n×n,N(t,i)∈n×n使得对三元组式(E,A(t,i),C(t,i))满足下述条件之一,则奇异随机Markov跳变系统(2)存在唯一解。 (i)[20] 其中A1(t,i),C1(t,i)∈r×r,C2(t,i)∈r×(n-r),C3(t,i)∈(n-r)×(n-r)。 (ii)[21] 其中Sn2(t,i)∈n2×n2是零幂的,且n1×n1,C2(t,i)∈n1×n2,n1+n2=n。 定义1[22]离散奇异随机Markov跳变系统(2)是: (Ⅰ) 正则的,如果对所有的i∈Ξ,det(sE-A)≠0; (Ⅱ) 无脉冲的,如果对所有的i∈Ξ,deg(det(sE-A))=rank(E); (Ⅲ) 均方稳定的,如果对任意的初始条件(x0,r0)∈n×Ξ,都有limt→∞ε‖x(t)‖2=0; (Ⅳ) 均方容许的,如果它是正则,无脉冲和均方稳定的。 下述引理2给出了离散奇异随机Markov跳变系统稳定性的相关结论。 引理2[21]离散奇异随机Markov跳变系统(2)是均方容许的,如果存在矩阵P(t,i)=P′(t,i),使得对每一个i∈Ξ,式(3)成立: E′P(t,i)E≥0 -E′P(t,i)E<0 (3) 考虑以下离散奇异随机线性Markov跳变系统: (4) 其中,x(t)∈n表示状态变量,u(t)表示博弈人1的控制策略,v(t)表示博弈人2的控制策略,其容许策略空间分别记为U,V。w(t)是实随机变量序列,且满足ε(w(t))=0和ε(w(t)w(s))=δts。rt是一个取值于状态空间Ξ={1,2,…,l}的Markov过程,rt和w(t)相互独立。当rt=i,i∈Ξ时,系数矩阵A(t,rt)=A(t,i),A1(t,rt)=A1(t,i),B(t,rt)=B(t,i)。对每一个给定的(0,x0)和(u(·),v(·))=U×V,二次型性能指标为: Jτ(u,v)=ε{x′(T)Fτ(T)x(T)+ (5) 当rt=i,i∈Ξ时,Rτ1(t,rt)=Rτ1(t,i)∈L∞(0,T;n×nu),Rτ2(t,rt)=Rτ2(t,i)∈L∞(0,T;n×nv),Q(t,rt)=Q(t,i)∈C(0,T;Sn),Mτ(T)∈Sn,τ=1,2。 定义2[22]对于控制策略u∈U,从方博弈人2的最优反应集是 R2(u)={v0∈V:J2(u,v0)≤J2(u,v)},∀v∈V策略u*称为主方博弈人1的Stackelberg策略当且仅当满足如下条件: 根据定义2,可知Stackelberg博弈的最优解也是一种均衡策略。 结合配方法,我们给出上述有限时间离散奇异随机Markov跳变系统的Stackelberg策略。 定理1对于系统(4),假设如下代数Riccati方程(i,j∈Ξ) (6) 其中: 存在解P1≥0∈Sn,P2≥0∈Sn。则系统(4)-(5)的Stackelberg策略存在,且为: u*(t)=K1(t,i)x(t),v*(t)=K2(t,i)x(t) 证明首先,博弈人1先采取策略u,作为从方,博弈人2在监视到博弈人1的策略后选择相应的策略v,这时考虑博弈人2的性能指标函数x′(k)E′P2(k)Ex(k),取值函数Y2(t,x)=x′(t)E′P2(t,i)Ex(t),以下为书写方便,省略t,有: 结合 (7) 把式(7)代入J2(u,v)中,可得: (8) 在式(8)中,对v求导,并令导数为0,得到: (9) (10) 把式(10)代入J1(u,v)中,得: v*′S12(t,i)v*] (11) 把式(9)代入式(11),得到: (12) 对式(12)进行配方,结合式(6)可得: 由于R(t,i)>0故有: 此时, u*(t)=K1(t,i)x(t) (13) 把式(13)代入式(8),可得: 由于S22(t,i)>0故有: 此时, 注1式(6)所示的代数Riccati方程组,可以借鉴文献[8]的严格LMI法进行求解。 首先介绍无限时间随机最优控制中的一个重要概念——随机稳定性。 考虑如下离散奇异随机Markov跳变系统: Ex(t+1)=A(t,rt)x(t)+B(t,rt)u(t)+A1(t,rt)x(t)w(t),t=1,2,… (14) 其中,x(t)∈n是状态变量,u(t)是容许控制过程,w(t)是实随机变量序列,且满足ε(w(t))=0和ε(w(t)w(s))=δts。 定义2[23]给定任意初始状态x(0)=x0,r0=i,系统(14)是(均方意义下)随机稳定的,如果存在一个反馈控制u(t)=K(t,i)x(t)(i∈Ξ),其中K(t,i)均为常数矩阵,使得闭环系统Ex(t+1)=[A(t,rt)+B(t,rt)K(t,rt)]x(t)+A1(t,rt)x(t)w(t)是渐近均方稳定的,即limt→∞ε[‖x(t)‖2]=0。 需要注意的是,与有限时间情形相比较,无限时间情形的不同之处表现为: (ⅰ) 系统(14)是时不变的且性能指标中的权重矩阵为常数; (ⅱ)当T→∞时,Fτ(rT)=0,τ=1,2; (ⅲ)要求系统(14)是均方稳定的。 考虑式(15)所示系统: (15) 两博弈人的二次型性能指标为: u′(t)Rτ1(t,rt)u(t)+v′(t)Rτ2(t,rt)v(t)],τ=1,2 (16) 其中,控制权矩阵Rττ(t,rt)∈Sn;状态权矩阵Qτ(t,rt)≥0∈Sn,τ=1,2。无限时间Stackelberg博弈问题定义如下: 定义4[22]对于控制策略u∈U,从方博弈人2的最优反应集是 R2(u)={v0∈V:J2(u,v0)≤J2(u,v)},∀v∈V 策略u*称为主方博弈人1的Stackelberg策略当且仅当满足如下条件: 假设1[16]系统(15)是均方稳定的。 采用与有限时间随机Stackelberg博弈策略相同的方法,可得无限时间离散奇异随机Markov跳变系统Stackelberg博弈问题(15)-(16)的均衡策略如定理2所示。 定理2在假设1的基础上,如果下述代数Riccati方程(17) (17) 其中: i)K2(t,i) 存在解P1(t,i)≥0∈Sn,P2(t,i)≥0∈Sn。则无限时间奇异随机Markov跳变系统Stackelberg博弈问题(15)-(16)存在线性状态反馈均衡解: u*(t)=K1(t,i)x(t),v*(t)=K2(t,i)x(t) 由于定理2的证明方法与定理1类似,不再赘述。 注2式(17)所示的代数Riccati方程组,可以借鉴文献[8]的严格LMI法进行求解。 借鉴前人研究成果,将上述所得结论应用于离散随机奇异Markov跳变系统的混合H2/H∞控制问题。为简单起见,只分析有限时间离散随机奇异Markov跳变系统的混合H2/H∞控制,无限时间的分析方法与有限时间类似,不再赘述。 考虑式(18)-式(20)所示系统: (18) (19) (20) 其中,x(t)∈n是状态向量,u(t)∈m2是控制输入,v(t)∈m1是外界不确定性干扰,A(t,rt)等系数矩阵的定义同上。 有限时间离散奇异随机Markov跳变系统的混合H2/H∞控制定义如下: 定义3[23]给定干扰抑制水平γ>0,如果存在(u*,v*)∈U[0,T]×V[0,T],使得 (ⅰ)|Lu*|T<γ,其中 |Lu*|T= (ⅱ)假设存在最坏干扰v*(t)∈V[0,T],将其带入系统(19),u*(t)最小化输出能量 当上述的(u*,v*)存在时,我们称有限时间H2/H∞控制问题是可解的。 根据文献[22],在非合作微分博弈的框架下,系统(18)的H2/H∞混合鲁棒控制策略可以这样描述:主者先确定一策略u(t)并提前宣布,然后从者根据宣布的策略而选择自己的策略v(t)。因为从者实施的策略会影响主者的成本泛函,所以主者在宣布其策略时必须要考虑到从者的反应[22]。进而将混合H2/H∞控制问题转化为Stackelberg博弈问题,而混合H2/H∞控制策略等价于求解系统(18)-(20)的Stackelberg策略(u*,v*)。故根据定理1,直接可得下述结论。 定理3对于系统(18),假设如下代数Riccati方程 (21) 其中 B1(t,i)) 存在解P1(t,i)≥0∈Sn,P2(t,i)≥0∈Sn。则系统(18)的鲁棒控制策略为: u*(t)=K1(t,i)x(t),v*(t)=K2(t,i)x(t) 探讨了离散奇异随机Markov跳变系统的Stackelberg博弈问题,分别得到了有限时间和无限时间情形下的Stackelberg均衡解存在的条件,并将所得结果应用于相应的H2/H∞控制问题,以期丰富微分博弈理论及其应用研究。2 有限时间随机Markov跳变系统的stackelberg博弈
2.1 问题描述
2.2 主要结论
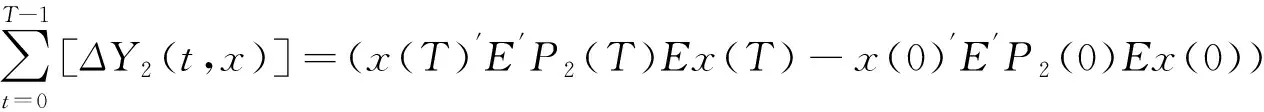
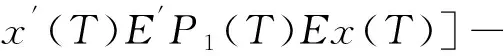

3 无限时间
3.1 预备知识
4 应用于H2/H∞鲁棒控制
5 结论

