用于HRRP 多类目标识别的D 距离分类器

姚璐，韩磊，杨磊，柴晓飞

（1. 西安电子工程研究所，陕西，西安 710000；2. 北京理工大学 机电学院，北京 100081）

雷达高分辨距离像是在大发射带宽、目标尺寸远大于雷达距离分辨率的条件下，目标散射点的子回波在雷达方向上投影的矢量和[1-5]. 由于其易获取、便于处理、占用存储空间少，以及包含丰富的目标结构信息等优点，利用HRRP 进行目标识别被认为是一种很有前景的雷达目标识别方法.

刘家锋等[6]指出，距离分类器是目前解决目标识别问题的主要方法之一，其思想直观、方法简单，但是由于其未考虑到目标类别内部的分类情况，识别精度有限. 基于此，诸多学者也基于不同的研究方向提出了多种基于HRRP 的识别算法以提高目标识别精度：(1)基于分类超平面提出了支持向量机（support vector machines，SVM），而且针对非线性问题后续引入了核函数、多尺度特征等多种解决方法.MALL 等[7]提出最小二乘向量机用于HRRP 目标识别，LIU 等[8]提出基于多尺度特征的模糊支持向量机，然而由于SVM 的边界是线性开放边界，因此会产生严重的重叠问题. (2)基于概率框架提出了贝叶斯分类器. DU 等[9]开发了一种基于贝叶斯稀疏学习的噪声统计模型进行噪声鲁棒雷达HRR 目标识别，但是基于贝叶斯的先验概率的计算一直是提高识别率的难题；(3)基于特征优化发展出子空间法. DAI 等[10]提出了多尺度融合稀疏保持投影方法用于提取包含更多判别信息的多尺度融合特征. 第四：基于自主提取深层特征引入了神经网络. LIAO 等[11]构建了基于级联深度神经网络的雷达HRRP 目标识别方法，但是神经网络需要训练大量的内置参数，因此需要大量的训练样本，而且容易出现局部最优、不能收敛或者过拟合的问题.

不过针对战场对抗环境下敌方非合作目标类型众多，且难以获得大量的训练样本，上述算法难以兼顾随着目标类型增加而明显增加的运算复杂度以及小样本时仍然具有优越的泛化性能，因此需要提出新的识别算法保证在进行多目标小样本识别时同时具备低的运算复杂度与优异的泛化性能，保证优越的识别性能.

通过利用比值计算两个向量之间的距离，本文提出一种新的距离计算方法，即比值距离，并将比值距离运用到距离分类器中进行目标识别，可以在进行多类目标识别时，保证分类器的运算复杂度很低，并且训练样本较少时，仍然具备优异的泛化性能，这两种性能能够确保分类器具有优异的识别性能. 本文将基于比值距离的分类器称为D 距离分类器.

1 D 距离分类器

1.1 比值距离的构建

诸多识别算法利用特征进行目标识别时，考虑到目标内部的特征分类情况，有的特征数量级过大，则在计算结果时所占比重会大，但其分布并非一定利于目标识别，所以一般会采用归一化方法将特征值的数量级缩放至同一区间，不过这种操作也会引发新的问题，因为并非所有数量级过大的特征都是不利于目标识别的特征，因此盲目的归一化也会将利于目标识别且数量级较大的特征与不利于目标识别且数量级较小的特征统一到同一数量级，反而会弱化算法的识别效果.

考虑到计算两个特征向量的比值距离时，无论对特征如何进行缩放，两点之间的比值距离不会受到影响，而且比值计算也会使得同等级的数量级相消，因而也不用考虑不同类特征数量级相差过大对结果所占比重不同的问题. 故此，基于以上思路构建比值距离用于对雷达HRRP 的目标识别.

针对小样本问题，主要是考验识别算法的泛化性能，特征提取一直是解决该类问题的重要途径，而正如公式（1）可见，比值距离的计算既可以解决不同类特征数量相差过大导致计算结果时比重相差过大的问题，也不会降低特征的可分性. 因此面对战场对抗环境下非合作目标无法获得大量训练样本的小样本问题，利用比值距离作为分类器的判别依据能保证更高的识别率.

另外，由于该比值距离分类器与欧式距离分类器类似，都属于模板匹配类型的识别算法，思想直观，计算公式简单，因此在目标类别数目增加时，增加的训练样本不会为识别运算量和训练难度增加过重的负担，即在对多目标进行分类时，依然能保证较低的运算复杂度，因此可用于对战场环境下多目标的识别.

为便于描述，本文将基于比值距离作为判别依据的分类器统称为D 距离分类器.

1.2 基于D 距离分类器的目标识别流程

基于D 距离分类器的目标识别流程与传统的分类算法相同，包括训练阶段与识别阶段两部分，其识别流程如图1 所示.

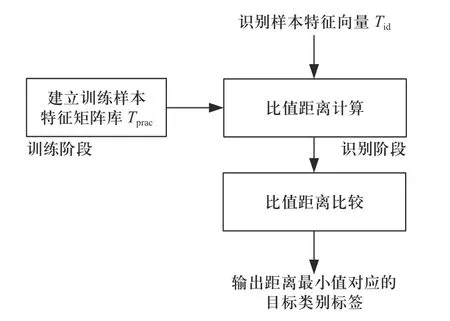
图1 D 距离分类器的识别流程Fig. 1 Recognition process of D distance classifier

1）D 距离分类器的训练阶段为建立训练样本特征矩阵库Tprac.

假设可用于训练的样本数目为m，每个样本提取n类特征，则可建立训练样本特征矩阵库Tprac，见公式（2），训练样本特征矩阵库Tprac包 含m×n个特征，其中每一个行向量为一个训练样本通过特征提取操作得到的训练样本特征向量.

首先计算输入的识别样本特征向量Tid与分类器存储的训练样本特征矩阵库Tprac中每一个行向量之间的比值距离，可以得到m个距离值，具体计算过程可见公式（4）.

其次对m个比值距离进行大小比较；

最后输出比值距离最小的训练样本对应的目标类别，就是D 距离分类器对输入样本的识别结果.

1.3 D 距离分类器的优势

与传统的HRRP 自动目标识别算法相比，D 距离分类器具有优异的泛化性能以及很低的运算复杂度，从而保证其具有优异的识别性能，主要创新优势在于：

1）在计算两个特征向量之间的距离时，未采用传统的欧式距离，而是改为比值距离，这种距离计算方法能够在消除不同类特征数量级差异时避免降低利于目标分类的特征的权重、提高不利于目标分类的特征的权重这一情况的发生，从而能够保证D 距离分类器具有优异的泛化性能；

2）因为D 距离分类器的思想直观，计算公式简单，因此具有较低的运算复杂度，当待识别目标类别数目增加时，同样能够保证很高的识别精度；

3）对输入的特征值直接进行距离计算，不需要进一步的特征优化同样能保证很高的识别精度，这一特点能够优化距离分类器的运算步骤.

2 实验结果与分析

采用8 类地面目标的一维距离像实测数据，来验证D 距离分类器进行多类目标识别时的识别性能，包括泛化性能以及计算复杂度两部分. 如表1 所示，8 类地面目标可分为军事目标与非军事目标两大类，其中军事目标包括4 类，非军事目标包括4 类.

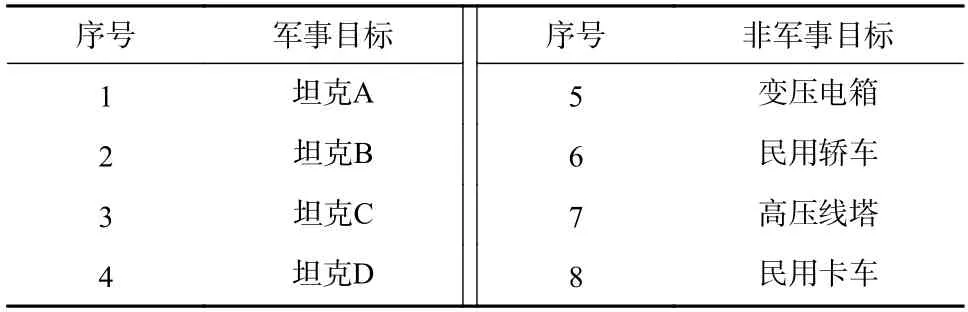
表1 用于进行分类器性能验证的8 类地面目标Tab. 1 Eight ground targets used for classifier performance verification

对地面目标的距离像进行平均距离像降噪等预处理，所得的全部图像用于训练与识别，总样本数为6 681；对预处理后的距离像提取15 类特征并利用Fisher 准则计算每类特征的类间距离与类内距离之比，取比值最高的前10 类特征用于目标识别，包括目标径向长度、强散射中心数目、二阶中心矩、方差、平均起伏特性、差分起伏特性、对称性特征、去尺度结构特征、径向能量特征、散射中心分布熵等. 八类地面目标关于方差、平均起伏特性、差分起伏特性三类特征的分布如图2、图3 所示.

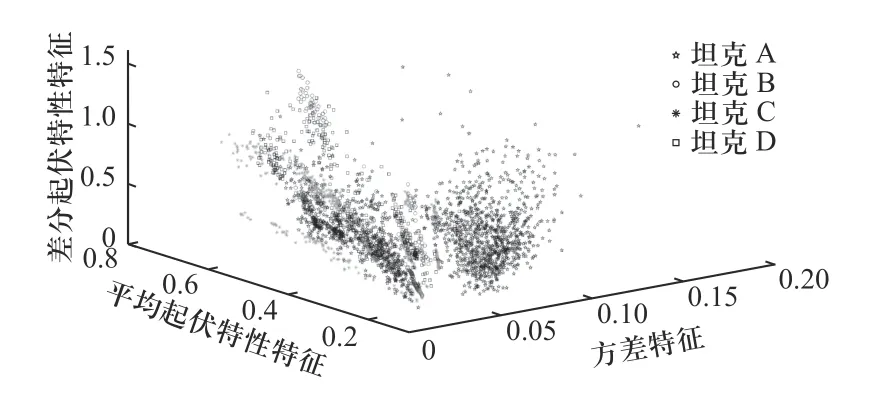
图2 4 类军事目标的特征分布Fig. 2 Characteristic distribution of four military targets

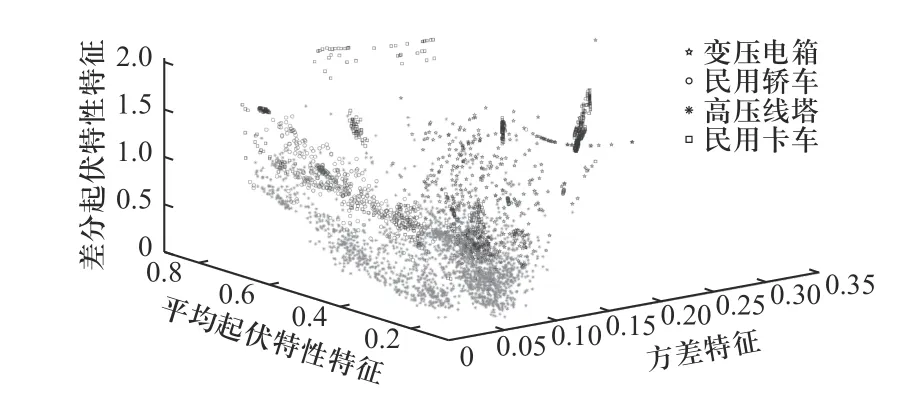
图3 4 类非军事目标的特征分布Fig. 3 Characteristic distribution of four non-military targets

与D 距离分类器进行对比分析的识别算法包括：进行特征优化的欧式距离分类器、LDA 分类算法、朴素贝叶斯（Naive Bayes）分类器、可用于多目标分类的支持向量机（SVM），BP（back propagation）算法.

算法运行平台为MATLAB2020b.

2.1 D 距离分类器泛化性能的分析

识别算法的泛化性能优劣可通过比较少训练样本情况下识别算法的识别精度得出. 当训练样本的比例从10%～90%逐次递增时时，各分类算法的识别精度如表2 所示，变化趋势如图4 所示.

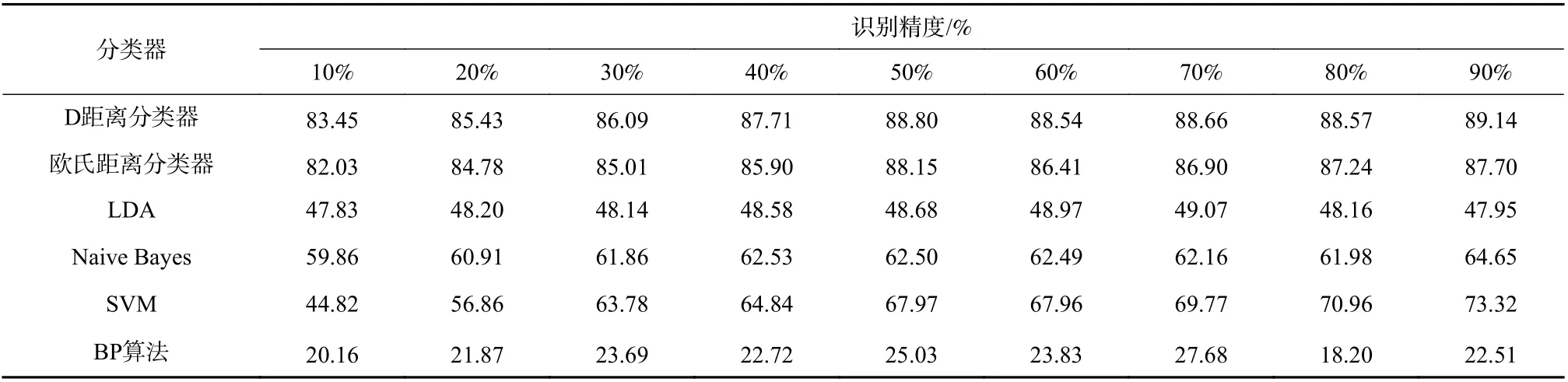
表2 训练样本比例变化时，各分类算法的识别精度Tab. 2 Recognition accuracy of each classification algorithm with different proportion of training samples

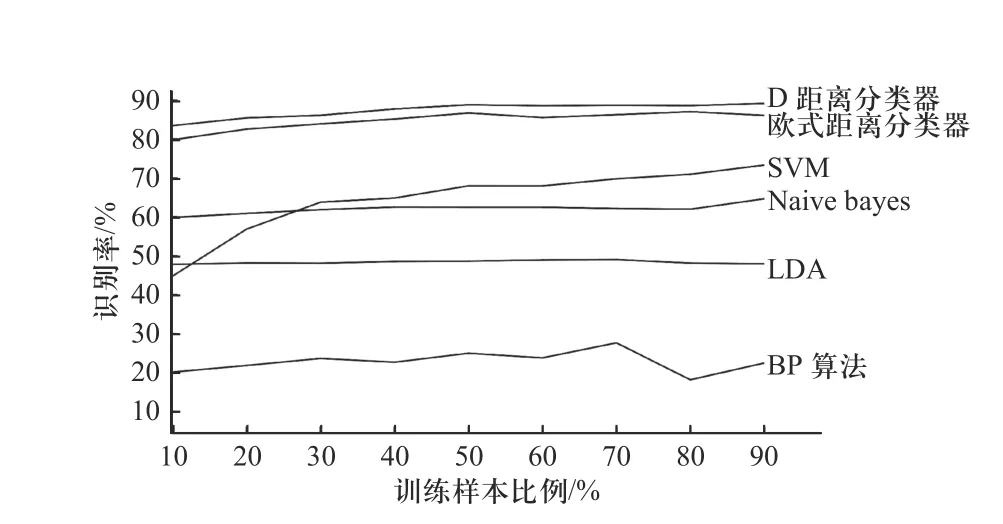
图4 训练样本比例变化时，各分类算法的识别精度变化趋势Fig. 4 Recognition accuracy’s change trend of each classification algorithm with different proportion of training samples

分析表2 与图4，可以发现在对八类地面目标进行分类时，在训练样本的比例从10%逐次递增到90%的过程中，D 距离分类器的识别精度始终是6种分类算法中最高的，而且当训练样本的比例分别为10%与90%时，识别精度仅相差5.69%，说明D 距离分类器在待分类目标类别数目为8 且训练样本数目很少时，依然能够保证很高的识别精度. 可得出结论，本文提出的D 距离分类器在利用一维距离像进行多类目标识别时具有优越的识别性能与泛化性能.

传统的距离分类器同样具有优越的识别性能与泛化性能，但稍逊于D 距离分类器；SVM 的识别精度随着训练样本比例的提高有很明显的提升，说明针对本文的实测数据该算法的泛化性能一般；朴素贝叶斯与LDA 两类算法的识别精度太低；以BP 算法为代表的深度神经网络在本次实测验证时表现最差，通过分析训练过程，发现神经网络总是进入无法收敛的状态，因此无法确定最优模型，从而导致识别效果过差.

2.2 D 距离分类器识别运算复杂度的分析

算法的识别运算复杂度主要体现在当待识别目标类别增加时，随着识别运算量与训练难度增加，其识别精度降低的程度. 当训练样本的比例为50%，待识别目标的类别数目分别为2、4、6、8，从识别样本中选取一组特征向量用于目标识别，循环测试500 次，计算6 种识别算法的平均训练时长以及平均识别时长，数据列于表3. 需要注意的是，待识别目标的类别数目增加时，是在原有待识别目标已有的训练样本的基础上直接添加新的待识别目标的训练样本，识别样本也更新为数据库内当前所包含的目标的识别样本，因此，待识别目标的类别数目分别为2、4、6、8 时，训练样本的数目也是增加的，识别样本也是增加的.

分析表3 数据，可以发现随着待识别目标的类别数目增加时，每类算法的训练时长都会持续增加，但是识别时长仅有D 距离分类器与欧氏距离分类器有明显的增加，这是因为该两类分类器采用的是模板匹配法，分类器内部储存的是提取的特征而不像其他识别算法存储的是公式以及训练过程计算的参数，因此随着待识别目标数目的增长，该两类分类器内部存储的参数增多，识别时长自然会增加，另外4类算法的识别时长基本保持在同一水平，说明分析识别时长不能体现出识别算法的计算复杂度；当待识别目标的类别数目增加时，每类算法的训练时长都会持续增加，其中BP 算法体现的最为明显，当目标数目变为6 时，50%的样本根本无法训练出能够用来识别的神经网络，说明神经网络内部运行复杂，而D 距离分类器的训练时长增加缓慢且在各个待识别目标数目时一直用时最短，其次用时短且增长缓慢的是欧式距离分类器，说明待识别目标类型的增加不会给基于模板匹配的两类分类器增加过重的训练负担.

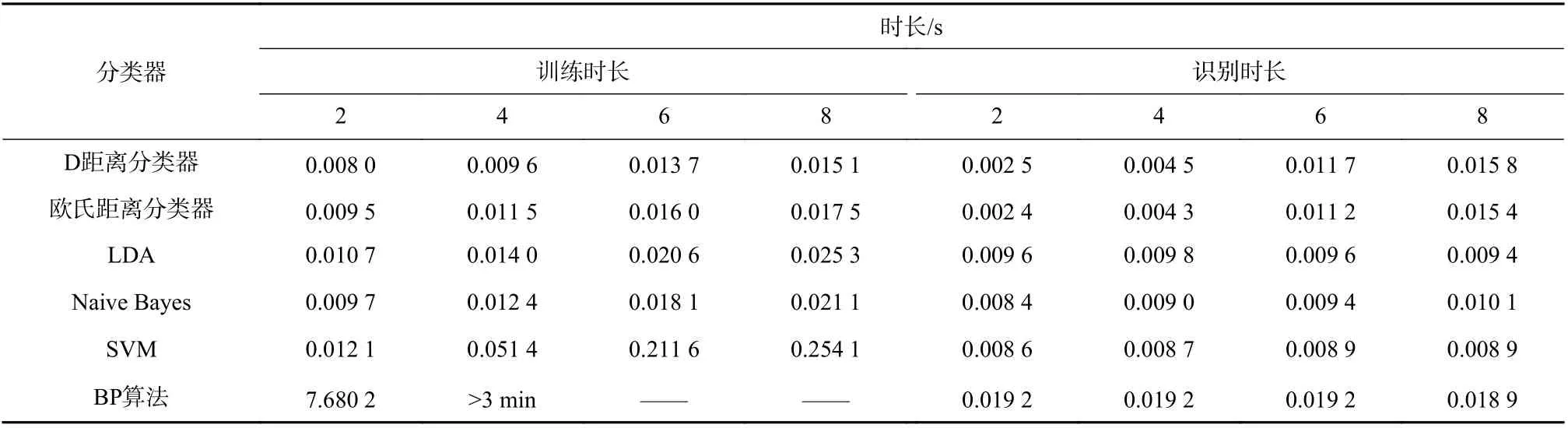
表3 待识别目标类别数目变化时，各算法的训练时长与识别时长Tab. 3 Training durations and recognition durations of each classification algorithm with identified target categories number

当训练样本的比例为50%，待识别目标的类别数目分别为2、4、6、8 时，6 种识别算法的识别精度被列于表4，变化趋势可见图5.

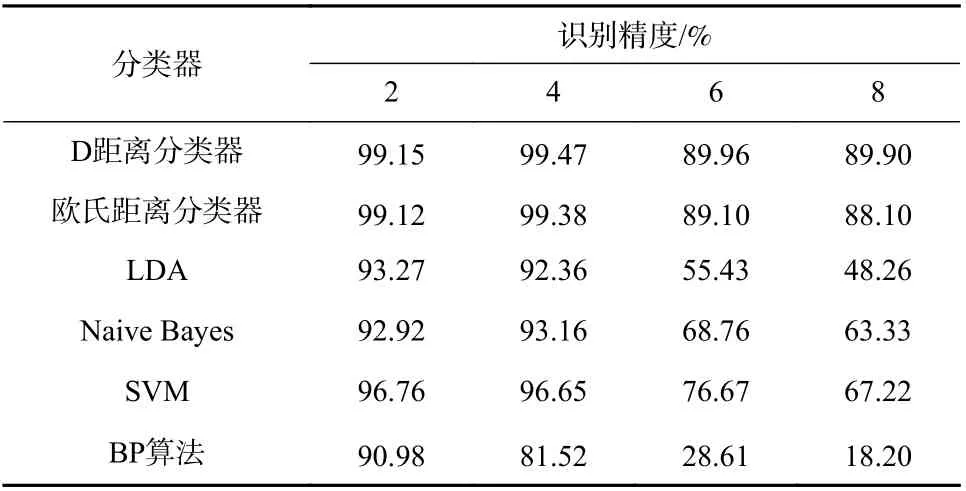
表4 待识别目标的类别数目变化时，各算法的识别精度Tab. 4 Recognition accuracy of each classification algorithm with different target categories number

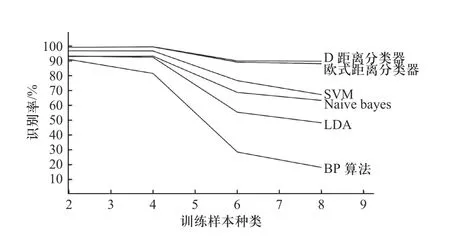
图5 待识别目标类别数目变化时，各算法的识别精度变化趋势Fig. 5 Recognition accuracy’s change trend of each classification algorithm with identified target categories number

观察表4 与图5，可发现随着待识别目标类别数目的增加，所有算法的识别精度都有不同程度的下降，而D 距离分类器的下降是最少的，其次是欧式距离分类器，结合表3 中D 距离分类器的训练时长是最短且增长缓慢的特点，可以说明随着待识别目标数目的增加，D 距离分类器的识别运算复杂度的增加是最缓慢的，可以保证在目标种类增加时，具有优于其他算法的识别性能.

3 结 语

本文提出一种利用比值计算两个向量距离的新方法，并将比值距离应用到距离分类器中形成一种新的距离分类器即D 距离分类器，进行基于HRRP 的雷达自动目标识别. 通过八类地面目标实测的距离像进行验证可知，D 距离分类器不仅具有优异的泛化性能，而且随着待识别目标的种类增加时，其识别运算复杂度仍能保持很低的水平，从而保证D 距离分类器在进行多类目标识别且训练样本有限时，仍然具有优异的识别性能. 目前仅验证了D 距离分类器在基于HRRP 的雷达自动目标识别领域的性能，而且由于计算公式使用了比值计算，因此需要确保D 距离分类器中储存的特征值均为非0 的数值.