基于多阶段评价选择遗传算法的材料订购和运输最优化问题研究
王子怡
(西南林业大学大数据与智能工程学院,云南 昆明 650051)
1 研究背景
本研究中的某建筑企业所用原材料主要是木质纤维和其他植物素纤维材料,总体可分为A、B、C 3种类型。该企业计划每年按48周安排生产,在生产之前,还需要提前制定24周的原材料订购和转运计划。因此,需要根据产能要求确定原材料的供应商和相应每周原材料的订购数目,并在最后委托合适的第三方物流公司转运生产的原材料。该企业每周的产能为2.82万m3,每立方米产品需要消耗A类、B类或C类原材料。同时供应商供货量可能多余或少于订货量,所以企业需要保证库存里有不少于2周生产需求的原材料数目[1]。
2 基于TOPSIS的供应商重要性评价模型
2.1 供应商重要性评价体系
先衡量供应商对生产企业重要性的评价指标并给出具体定义,然后构建出供应商重要性衡量体系,具体如下。
失信次数ηi:供应商未按量供货(包括不供货的情况)的次数。
失信率α:供应商未能按量供货的次数占企业向该供应商订购次数的比例。公式为α=ηi/ηn,其中,ηi为供应商未能按量供货的次数(包含未供货的次数),ηn为生产企业向该供应商订货的次数。
供货次数ω:各供应商240周中提供货物的次数。
供货次率ψ:各供应商240周中提供货物的次数占240周的比例。公式为ψ=ω/N,其中N取值为240。
单周最大供货量β+:各供应商240周中供货量最大的1周的供货数量。该指标可以有效衡量供应商的最大供货能力,供应商的重要性很大程度体现在供应商的供货能力,从数据中可以得到各供应商5年来的最佳供货数据,从而可以分析该供应商的供应能力,有助于生产企业进行决策。
总供货量β:供应商240周总供货量。为了衡量供应商的供货实力,对供应商5年来供货总量的评定很有必要,供应商5年来能提供的货物数量在一定程度上反映了这家供应商的综合实力,这可以作为企业向供货商订购货物的依据,供货实力强的供应商,企业会优先考虑大额订单。
平均供货量β-:供应商平均每次供货的货物数量。公式为β-=εi/ηn,其中,εi为供应商5年总共提供的货物,ηn为5年来供应商向生产企业供货的次数。在供应商供货能力的评定上,需要比较均衡地了解每家供应商的供货能力,平均值是一组数据中最有代表性的统计量,其能较好地衡量出每家供应商的平均供货水平。
供货率ε:供应商提供的货物占企业订购货物的比例。公式为ε=βi/βn,其中,βi为供应商提供的货物数量,βn为企业订购的货物。衡量供应商供应能力的另一重要指标是供货过程中能提供的数量。
供货量标准差γ:反映供应商供货数据的离散程度,即240周总体供货量与平均供货量离差平方的算术平均数的平方根,公式为其中,βi为供应商每周提供的货物量,为240周平均每周提供的货物量。考虑到供应商每次供货量数值变化不确定,故需采用标准差对供货量进行分析,为了观察供货数据的波动性,衡量供应商的供货稳定性,采用该指标衡量供应商供货能力的波动性。
以上9个评价指标,可层次构成供应商重要性评价体系。
2.2 TOPSIS分析过程
TOPSⅠS(Technique for order preference by similarity to ideal solution)法是用于研究与理想方案相似性的顺序选优技术。可以理解为,数据越大越优,数据越小越劣,结合数据间的大小,计算正负理想解与评价对象的距离以及综合得分,最后得出优劣方案的排序[2]。
TOPSⅠS分析通常分为以下几步:①特征数据属性正向化处理;②正向化矩阵标准化得到标准矩阵M③找出最优矩阵向量M+和最劣矩阵向量M-;④分别计算评价对象与正理想解距离D+或负理想解距离D-;⑤计算各评价对象与最优方案的相对近似度C,进行排序即可得到结果。由TOPSⅠS方法可知,对供应商的失信率、供货率、供货量标准差、平均供货量、总体供货量等评价指标进行正向化处理和标准化处理后,建立TOPSⅠS模型。
2.3 数据预处理
对所有特征数据进行正向化处理即把所有指标转化为极大型,所有的数字越大,评分越高。对处理后的数据进行标准化处理,在多指标评价体系中,由于各评价指标的性质不同,通常具有不同的量纲,所以在数据样本充足的情况下,往往直接使用标准化对数据进行无量纲预处理,便于不同指标之间进行加权和求和。
综上可知,各个评价指标最终综合表现为与正理想解的相对近似度。相对近似度越大,供应商越重要。该相对近似度大小的确定需要根据9个指标的数据进行求解,求解过程及结果在下面模型求解中给出。
2.4 模型的求解
假设有n个待评价对象,m个评价指标的标准矩阵为M。取最优矩阵向量M+,取最劣矩阵向量M-,然后计算评价对象与正理想解的距离、评价对象与负理想解的距离,即可计算各评价对象与最优方案的相对近似度C。
计算得到综合排名前27的供应商如下:201、S140、S229、S361、S108、S151、S340、S282、S139、S275、S329、S308、S330、S395、S131、S356、S268、S306、S348、S194、S126、S352、S143、S307、S247、S284、S374。
3 遗传算法模型
3.1 供应商最少
该问题要求在尽可能满足生产需求的情况下选择最少的供应商数量。根据供应商重要性排名,综合考虑各供应商的供货能力和供货稳定性,考虑采用各供应商平均供货量来表示各供应商每周的供货能力。这里提出一个新的数量名词,出产量φ,即供应商提供的货物能为生产企业带来的产能,然后在50家最重要的供应商中按顺序累加其每周出产量直到满足生产需求,求出最少供应商数,即计算出的最少供应商数n为22。
3.2 最经济的订购方案
模型的建立。该问题要求制定未来24周每周最经济的原材料订购方案,实际上就是要从上文中的50家供应商中组合出最经济的方案。选择使用遗传算法进行迭代优化选择,遗传算法是根据基因变异的思想进行随机优化的搜索方法,结合自适应的概率优化算法,能够在全局范围内寻找最优解,满足题目要求,公式如下:
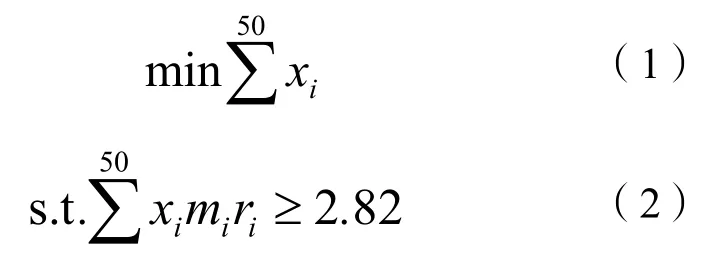
式(1)(2)中:xi为是否向第i个企业订货,xi=0或1;mi为第i个供应商的供货量;ri为该企业所提供材料的系数。

这是个0-1背包问题,很难用传统的线性规划求解,故本题设计用遗传算法来解决[3]。
首先,确定种群数量,给染色体编码,随机生产第一代种群;其次,确定个体评价方案,判断是否满足停止条件,若是则停止,输出最优解,否则继续进行操作,通常第一代种群不会满足停止条件;最后,对种群进行选择、交叉、变异操作,得到下一代种群,再进行评价,反复循环,直到满足生产需求。
其中遗传算法的主要流程如图1所示。
根据图1的算法流程,首先对种群进行编码,然后初始化种群并进行多阶段评价与选择,在一般的遗传算法中,通常只有一个评价和选择阶段。本文需要在满足生产的条件下,还要求价格最低,所以首先以供货量为评价指标来评价个体的适应性。在选择过程中,按供货量从大到小进行排序,淘汰后50%的个体。而第二阶段的评价与选择和上述过程一致,适应性指标换成了总价。选择过程采用升序方式,选择前50%的个体保留下来。
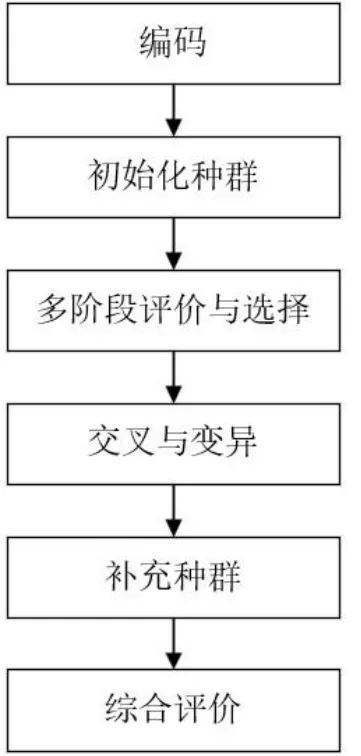
图1 遗传算法的流程
做完多阶段评价与选择后则进行交叉与变异和补充种群的操作。本算法在交叉和变异阶段进行了种群个体数量的补充。在生物界,交叉出现的情况比变异多,故在交叉阶段补充70%的个体,在变异阶段补充30%的个体。
最后是综合评价阶段。在迭代完成后,将所有个体按照供货量升序、价格降序联合排序,找出最接近于2.82万的个体作为输出结果。
根据以上算法得出原材料订购方案,如图2所示。
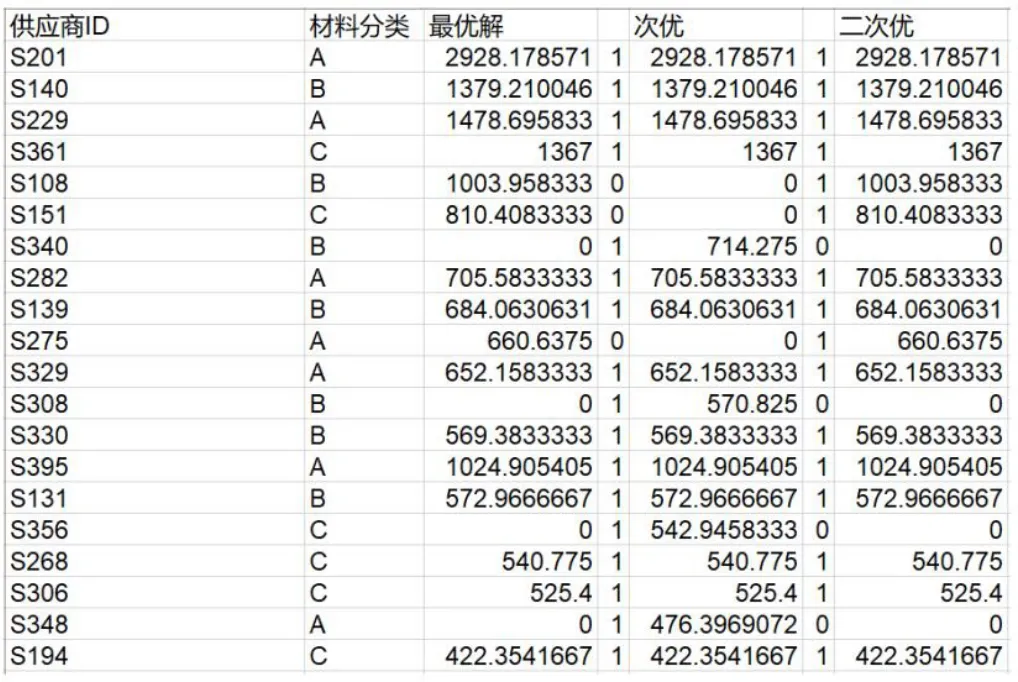
图2 原材料订购方案
图2中展示了最优解、次优解和二次优解的订货方案。例如最优解中首先选择了编号为S201的供应商,它的供货量为2 982.178 571。同时,分析本文将最优解、次优解和二次优解三者之间的差异可知,最优解与次优解有20个不同的供应商。
4 模型评价与推广
4.1 模型优点
采用遗传算法的优点如下:①快速随机的搜索能力;②搜索从群体出发,具有潜在的并行性,可以同时进行多个个体的比较;③搜索使用评价函数启发,过程简单。
采用Topsis综合分析方法的优点如下:①不需要目标函数,是无人监督的分析方法;②对于数据分布及样本量、指标多少无严格限制,可以既适用于小样本资料,也适用于多评价单元、多指标的大系统。
4.2 模型缺点
采用遗传算法的缺点如下:①遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码;②另外3个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验。
采用Topsis综合分析方法的缺点如下:①求解规范决策矩阵比较繁杂;②对于正理想解和负理想解的求解过程比较困难;③不确定指标的选取个数为多少,个数确定才能很好地去刻画指标的影响力度。

